Predictive analytics for crystalline materials: bulk modulus

Abstract

The bulk modulus is one of the important parameters for designing advanced high-performance and thermoelectric materials. The current work is the first attempt to develop a generalized model for forecasting bulk moduli of various types of crystalline materials, based on ensemble predictive learning using a unique set of attributes. The attributes used are a combination of experimentally measured structural details of the material and chemical/physical properties of atoms. The model was trained on a data set of stoichiometric compounds calculated using density functional theory (DFT). It showed good predictive performance when tested against external DFT-calculated and experimentally measured stoichiometric and non-stoichiometric materials. The generalized model found correlations between bulk modulus and features defining bulk modulus in specific families of materials. The web application (ThermoEl) deploying the developed predictive model is available for public use.

---

I. Introduction

The bulk modulus of a material is a physical parameter that reflects bonding character in crystals. It is mainly used as an indicator for crystal hardness^1,2 and resistance to fracture strength.³ The applications of the bulk modulus should not be seen as limited to the optimization of mechanical performance of materials. As a parameter defined by elastic properties of the material, bulk modulus could be involved into tuning other properties of similar flavor. For example, it could be employed in optimization of nanostructured materials for low thermal conductivity applications,⁴ or for estimation of intrinsic charge carrier mobilities⁵ in band conductor stoichiometric compounds. The ability to predict bulk modulus for a compound or material of a given composition opens up multiple possibilities for advancing design of novel thermal barriers, higher efficiency thermoelectric energy convertors, phase-change memory, heat-assisted magnetic recording, thermal management of nanoscale electronic devices, and many more.

The task of addressing the bulk modulus for localized regions of chemical compound space has been approached earlier. All prior attempts to generate analytical models for prediction of bulk modulus could be divided into two groups. The first approach uses small size experimentally measured data sets that is later approximated with linear regression.^6,7 The second approach utilizes extensive data sets generated with help of Density Functional Theory (DFT). The relatively large size of the data set seems to be a plus since more advanced analytics such as artificial neural networks could be used in modeling.⁸ However, the accuracy of DFT-based predictive analytics is strongly affected by the performance of specific functional or pseudopotential,^9–11 and techniques used during experimental measurements to evaluate DFT data. In order to reproduce and predict experimental values correctly, the DFT training data should account for thermal effects that are rarely taken into account in standard DFT calculations.

The application of data science techniques in materials science has given rise to the emerging field of materials informatics.^12–16 In the current work, we present the first attempt to move away from analytical models specific to small regions of compound space. In order to address our interests in thermoelectric applications, the publicly available TE Design Lab database¹⁷ was selected for training a predictive model. Here, thermal effects in bulk modulus values are addressed by the Birch–Murnaghan fit.^18,19 Sampling of compound space for training of predictive model was done evenly across materials of different composition (from unary to quinary) and space groups (Fig. S1 and S2 in ESI Part S1†). The random forest model proposed as solution in the current work utilizes an ensemble of decision trees which has been proven to generate state of the art prediction performance for diverse data sets. In order to allow easy utilization of the proposed predictive model by rest of the scientific community, we have also deployed it as a part of our user-friendly web application ThermoEl²⁰ (ESI, Part S4†).

II. Methods

In current work we used TE Design Lab database after it was cleaned from duplicates and outliers. Density functional theory was used for calculation of bulk moduli. Those calculations are not part of this work and could be found elsewhere.²¹ TE Design Lab database contains diverse types of experimentally studied structures such as halides (Cl, Br, I), oxides, chalcogenides (S, Se, Te), pnictides (N, P, As, Sb, Bi), and so on. The preprocessed data was separated into five groups based on its elemental composition (Table S2 in ESI Part S1†). Approximately 20% of compounds were randomly withheld from each group for further estimation of model performance. The rest of compounds were used for building 10-fold cross validated regression models. Regression was performed with random forest algorithm as implemented in the Scikit-Learn library in Python 2.7 language. Hyper parameters were optimized using grid search as implemented in Scikit-Learn.²²

The optimization of the predictive performance was based on stepwise reduction of the top N ranked attributes (Table S3 in ESI Part S1†). A series of 10-fold cross-validated models were evaluated based on the set of statistical metrics: the correlation coefficient (R), coefficient of determination (R²), mean absolute error (MAE), root mean squared error (RMSE), relative absolute error (RAE), and relative squared error (RSE). The model utilizing N = 50 attributes was found to have the best predictive performance. This model was used further in “Results and discussion” section.

All attributes used could be classified into three types. A thorough description of the full set of attributes was given in our introductory publication on ThermoEl tool kit.²³ Elemental properties we considered fall into three categories: (i) location of the element in the periodic table, (ii) fundamental properties of the elements, (iii) experimentally measured properties of pure elements in their crystalline states. Properties within category (i) include atomic number, period, and group, and whether or not the element can be classified as an alkali, alkaline earth, transition metal, post transition metal, metalloid, lanthanide, actinide, non-metal, halogen, or noble gas. Properties within category (ii) include atomic weight, molar volume, Pauling's electronegativity, covalent radius, atomic radius,²⁴ ionic radius,^24–26 pseudo-potential radii sum of Zunger,²⁷ amount of valence electrons by Villars,²⁸ total number of valence electrons as well as specified by their s-, p-, d-, and f-character, and overall number of unfilled valence orbitals as well as those of s-, p-, d-, and f-character. Finally, properties within category^29–32 (iii) include crystal radius, melting point, boiling point, density, heat of vaporization, thermal conductivity, electron affinity, ionization energy, and ground-state crystal structure of the element.

For each material we find if at least one element in the chemical formula belongs to certain categories in the periodic table (and subsequently set the corresponding attribute from group (i) to 1). We also calculate minimum, maximum, sum, mean, and mean absolute deviation from the mean value of elemental-based attributes (from groups (ii) and (iii)). The same set, marked with * symbol (see Table S4, Part S2 in ESI† section for details), was also calculated for the coefficient-weighted atomistic-based attributes. The coefficients used for coefficient-weighted attributes were generated from the chemical formula of the unit cell (data extracted from ICSD database). In other words, chemical formula of the unit cell is equal to _cell_formula_units_Z multiplied by the number of the formula units as specified by _chemical_formula_structural, _chemical_formula_moiety or _chemical_formula_sum. In order to account for disorder in experimental samples, the structural information was extracted from ICSD database (not DFT calculations). Extraction was possible since corresponding ICSD codes are available in the TE Design Lab database.

Due to the presence of typos in selected cif-files we had to recalculate derived attributes such as crystallographic cell volume and crystal density difference from original crystallographic parameters. We also introduced a new characteristic of the crystallographic cell, which we call crystal electronic density, and is not available in ICSD database.³³ It provides information on overall electron density in the unit cell, and is calculated as following:

where N is total number of atom types in the chemical formula of the unit cell, number of electrons_i is the atomic number of atom i; atomic coefficient_i is coefficient of atom i in the chemical formula; crystallographic cell volume is volume of crystallographic cell.

III. Results and discussion

a. Generalized model and its performance

Our approach in this work is to use machine learning for building a generalized predictive model for bulk modulus. In pursuing this goal, we started with (Fig. 1) data selection. Aside from many earlier attempts, we did not fit the selected parameters of a linear regression model to the reference data. We allowed ensemble learning to figure out the relationship between feature-space of the training data and bulk modulus values. An initial set of 364 attributes (see Methodology) was gradually reduced to 10 by shortening the list at each step of model optimization. The unique set of attributes ranked at previous step was used to generate random forest model at the next step. The accuracy of each model was estimated with 10-fold cross-validation procedure. Based on the combination of different statistical parameters (Table S3 in ESI Part S2†), the model based on 50 attributes was selected as the best generalized model.

Fig. 1 Workflow of current study. See Table S2 (ESI Part S1†) for details on splitting into withheld and work sets.

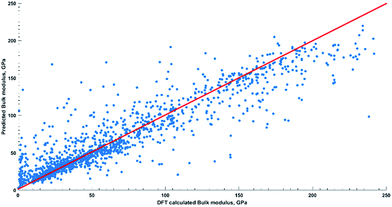
From the mean absolute error (MAE = 13.58 GPa) of the generalized model and visualization of predicted values (Fig. 2) one could see overall good performance of the model. It has uniform predictive power for all groups of compounds as well. For example, mean absolute error for unary, binary, ternary, quaternary, and quinary groups is equal to 8.51 GPa, 16.61 GPa, 12.53 GPa, 9.82 GPa, 9.8 GPa, respectively. We also report that MAE < 50 GPa is observed for 100%, 92.34%, 95.78%, 98.59%, and 100% of aforementioned group types. The general feature of outliers (MAE ≥ 50 GPa) is dominance of oxygen containing species regardless of group type.

Fig. 2 Performance of the best generalized model according to 10 fold cross-validation.

Now we would like to address two concerns typical for machine learning models. Those are accuracy of the model within the same compound space, and transferability to compounds from materials space not sampled by the training set. In order to address accuracy of the model within the same compound space as in training set, the subset of data was collected from each group of compound in the TE design database before we start working on the model (Fig. 1 and ESI Part S1†). In addition to cross validation, our generalized model was also tested against the withheld set of 356 compounds (Fig. 3) and showed good quality predictions (R = 0.93; R² = 0.86; MAE = 11.80; RMSE = 18.75; RAE = 30.45%; RSE = 14.20%). The only seven outliers (MAE > 50 GPa) are members of binary and ternary groups and possess different space groups. Six out of seven have oxygen element in their composition.

Fig. 3 Machine predicted vs. DFT calculated bulk moduli for withheld set of 356 materials.

On the transferability point, it is worth noting that the predictive capabilities are limited to bulk modulus values up to 250 GPa (Table S1, ESI Part S1†). Therefore, bulk modulus for materials such as diamond and SiO₂ will be underestimated. If the entire materials space is represented by clusters of unary, binary, ternary, quaternary, and quinary compounds, then our model is expected to produce less accurate predictions for unary and quinary compounds, since those are the least sampled groups in the training data set. However, from the distribution of bulk modulus values within different types of compounds (Fig. S3 in ESI Part S1†), one can see that such envisioning of materials space is incorrect. Therefore, the only way for us to discuss transferability is to test our model against the experimental data whenever available. It is especially an interesting exercise, since bulk modulus ground truth values in TE design lab database (and therefore in our model) are based on theoretical estimations coming from DFT-based calculations.

The main problem we faced here is to find studies reporting both experimentally measured bulk modulus value of the material, and information on its crystallographic structure (space group and crystallographic cell dimensions). On top of it, most experimentally reported values of bulk modulus are measured for non-stoichiometric doped materials or polycrystalline materials. For the cases when the space group is determined or suggested, we supplemented structural information from appropriate entries in the inorganic crystal structure database (ICSD). For the polycrystalline samples with unknown structural information, we made predictions for all available ICSD entries of the same chemical formula. If exact compound was not listed in the ICSD, we used the next similar composition compound. All details on this comparison are available in Table S5 (ESI Part S3†).

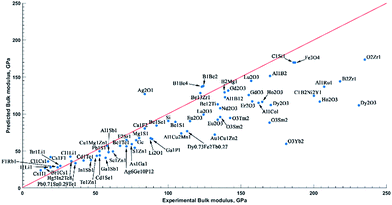
For this test, we avoided any compound used for model training. In addition, experimental set used here has few elements (F, Dy, Yb, Sm, Nd, Lu, Ho, Gd, Eu, Er) absent in the training set. Visualization of predicted values (Fig. 4) revealed good performance (deviation from experiment <50 GPa) for 85% of experimentally studied materials with exception of lanthanide oxides. It might be partially explained by the fact that among all lanthanoid elements, only lanthanum was present in training set. At the same time, we see very good predictions for calcium fluoride and strontium fluoride despite the absence of alkaline halides in the training set. It seems that model trained on transitional metals forecasts well for alkaline halides, and for fluorides in particular.

Fig. 4 Experimental vs. predicted values of bulk modulus. Here predicted bulk modulus value for each compound was obtained through averaging over all values predicted on the set of structures of the same formula. Experimentally measured bulk modulus is either averaged (whenever available) or the most recent value is taken if huge deviation among measurements is reported. We exclude cases where exact formula of the compound could not be found in the ICSD.

Intermediate scale deviation from ground truth (red line in Fig. 4) is detected for polycrystalline thin slabs and multi-phase materials (Al1Ru1 and C1B2Ni2Y1). A possible reason for this could be that we assessed attributes with single space group structures due to lack of representatives in the ICSD. The last on the list of outliers is ZrB₂. The bulk modulus for this compound is underestimated despite the presence of binary compounds of zirconium with other non-metal elements (S, C, O) in training set. Finally, we would like to highlight the striking advantage of our model over any other published predictive model on bulk modulus. Despite training only on stoichiometric compounds, the current algorithm allows to predict non-stoichiometric materials as well. As proof of concept, we refer to the outstanding predictions of bulk modulus for Pb_0.71Sn_0.29Te, Hg_0.7Mn_0.3Te, and Dy_0.73Fe₂Tb_0.27 materials (difference with experimental values from 3 GPa to 36 GPa). This is especially encouraging since a vast majority of bulk modulus experimental measurements are done for non-stoichiometric compounds. Our model opens up a possibility to step ahead from idealized DFT-based compounds space into the actual world of experimental materials.

b. Key-features of bulk modulus according to generalized model

Next, we analysed most important features (Fig. 5) in the model. It would be interesting to see if our generalized model can find trends reported by prior works that studied specific families of materials. For example, it was reported^34–36 that bulk modulus has reverse correlation with molar cell volume or the cell volume for doped cobaltate perovskites, alkaline earth chalcogenides, ionic halides, and transition metal diborides. Some groups also reported^35,37,38 linear correlation between the bulk modulus and the bond length in binary semiconductors. Some features found to be correlated with bulk modulus in experimental or theoretical studies are excluded in the present study. For example, earlier discovered correlation between bulk modulus and Debye temperature,^37,39 the bulk modulus–volume–ionicity relationship,^40,41 between bulk modulus and plasma energy,^42–44 and so on. The reason for not using some known to be important features in the current machine learning study is their sporadic availability for majority of compounds.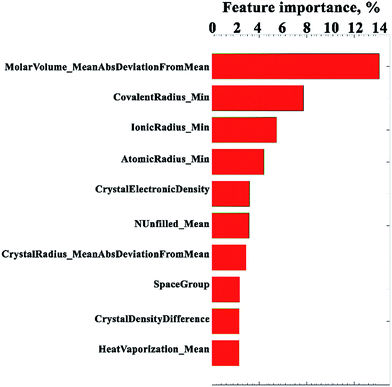

Fig. 5 Top 10 important attributes in the generalized random forest model. The attribute labels are self-explanatory. Full description of labels could be found in (Fig. S4 and Table S4 ESI Part S2†).

It is interesting to note that our machine learning technique did not select (Fig. S4 and Table S4 in ESI Part S2†) the same descriptors to be as important as they were stated in earlier studies specific to selected groups of materials. For example, the cell volume, coded here as crystallographic cell volume, is found to be only ranked 18th in the list of important parameters as determined by the random forest regression model. Instead, we found that the most important is the parameter reflecting average difference between atomic molar volumes and their average value in the compound, molar volume_mean abs deviation from mean. This parameter could be used as characterization of heterogeneity in the crystal, and an analogue of upper bound estimation of atomic packing in the cell.

The first-principles calculations done by Niu et al.¹ revealed the correlation between the brittle/high-strength properties of Al₁₂W-type compounds and the specific character of their chemical bonding. They showed importance of electron induced covalent strengthening mechanism, which alters chemical bonding upon the introduction of extra-valence electrons in the matrix of parent materials. In line with Niu's discovery, our model also stressed the importance of chemical bonding for prediction of bulk modulus. The top 2nd to 4th important attributes are minimum values of covalent, ionic, and atomic radii of chemical elements comprising the compound. A bit lower on the rank, the 7th attribute labeled as crystal radius_mean abs deviation from mean characterizes distribution of crystal radii in a compound. We believe that the model could not limit itself to single radius type because compounds of various bonding types and crystal structures are presented in the training set.

An earlier theoretical study³⁵ performed on diamond and zinc-blende solids suggested that bulk modulus should scale as the Fermi energy divided by the volume per electron. In other words, besides other factors, bulk modulus might correlate with the electron concentration. We introduced a somewhat analogous attribute, crystal electronic density, which, in our opinion, is also a great parameter to characterize electronic effects mentioned by Niu in the material matrix. The crystal electronic density is a universal density parameter that provides macro characterization of the cell regardless of its bonding character and composition. This parameter appears to be the top 5th contributor to bulk modulus. It is followed by N_{Unfilled_mean} attribute that estimates average amount of unfilled valence orbitals. The N_{Unfilled_mean} does not relate to molecular orbitals as a linear combination of atomic orbitals. It is calculated by simple arithmetic averaging of unfilled orbitals of all atom types in a compound. Despite the fact that Sekar et al.⁴⁵ speculated about the significance of empty orbitals for the bulk modulus in some semi borides, and N_{Unfilled_mean} attribute seems to support them, it should be noted that this attribute is a rather rough characterization of such electronic property of a material.

Going down the list of importance one could see attributes that logically should be linked with mechanical properties. Those are space group and crystal density of material. We anticipated bulk modulus correlation with crystal density, since crystal density is affected by radii present in the structure. The correlation “cationic radii → bulk density → bulk modulus”, was known for lanthanide sequioxides.⁴⁶ The 10th attribute is based on the heat of vaporization or enthalpy of vaporization of chemical elements averaged within compound composition. Heat of vaporization is the energy needed to be added to the substance in order to transform it into a gas. It is directly proportional to the bond strength in the solid.

We see a steady decline of importance after 10th attribute. Among those we would like to briefly mention attributes not based on already discussed parameters. Despite their lesser importance, these properties provide characterization of structure and composition of the material: electronegativity, ionization energy, the melting and boiling point of elements, location of elements in the periodic table, presence of alkali elements in the material, as well as experimentally measured crystallographic cell dimensions. The significance of electronegativity was also reported⁴⁷ for modelling of bulk moduli in A^NB^8−N as well as in binary A_mB_n and polymorphic ABO₄ type of compounds. We would like to stress that our generalized model indeed captured most physical trends known from various empirical models specific for localized regions of the compound space.

IV. Conclusions

In this work, we successfully employed machine learning techniques to the problem of bulk modulus prediction. The decision trees-based algorithm together with a unique set of attributes resulted in the development of a useful tool for predicting this mechanical property of stoichiometric and non-stoichiometric materials. Forecasted bulk moduli were close to experimental ones despite the fact that our model was trained using DFT calculated data. We have implemented the current algorithm into our online tool ThermoEl²⁰ for further utilization by rest of the materials community. The ThermoEl toolkit is an example of a generic tool unifying knowledge from different experimental and theoretical databases into a single computational representation. Here we attempted to produce a user friendly tool for prediction of mechanical properties across multiple (from bulk to nanostructured materials) spatial scales.

The current work provides machinery for advancing expensive and highly inefficient trial-and-error experimental approach for screening potential candidates for novel applications. Despite obvious success one shall not stop at current model level. It is clear now that structural features at different scales are crucial for properties of materials. Details of structuring in a material is subject to intrinsic properties of its elements and synthesis conditions. We believe that extension of our model with details on materials production will significantly improve its accuracy. To the best of our knowledge, information on different materials production in a standard format is not available. If such information is collected and combined with machine learning, one can potentially end up with a fully automatic approach for screening of novel materials.

Acknowledgements

This work is supported in part by the following grants: DARPA award N66001-15-C-4036, NIST award 70NANB14H012; AFOSR award FA9550-12-1-0458; NSF award CCF-1409601; DOE awards DE-SC0007456, DE-SC0014330. The access to TE design lab database has been provided through Citrination in accordance with requirements of the SIMPLEX project.

References

1. H. Niu, X.-Q. Chen, P. Liu, W. Xing, X. Cheng, D. Li and Y. Li, Sci. Rep., 2012, 2, 718.
2. J. Haines, J. M. Leger and G. Bocquillon, Annu. Rev. Mater. Res., 2001, 31, 1–23.
3. L. S. Dimas, D. Veneziano, T. Giesa and M. J. Buehler, J. Mech. Phys. Solids, 2015, 84, 116–129.
4. W. Chen, J.-H. Pöhls, G. Hautier, D. Broberg, S. Bajaj, U. Aydemir, Z. M. Gibbs, H. Zhu, M. Asta, G. J. Snyder, B. Meredig, M. A. White, K. Perssonae and A. Jain, J. Mater. Chem. C, 2016, 4, 4414–4426.
5. J. Yan, P. Gorai, B. Ortiz, S. Miller, S. A. Barnett, T. Mason, V. Stevanovíc and E. S. Toberer, Energy Environ. Sci., 2015, 8, 983–994.
6. C. Lia, Y. L. Chinb and P. Wu, Intermetallics, 2004, 12, 103–109.
7. S. Zhang, H. Li, H. Li, S. Zhou and X. Cao, J. Phys. Chem. B, 2007, 111, 1304–1309.
8. N. Artrith and A. Urban, Comput. Mater. Sci., 2016, 114, 135–150.
9. A. D. Corso, J. Phys.: Condens. Matter, 2016, 28, 075401.
10. K. Lejaeghere, L. Vanduyfhuys, T. Verstraelen, V. V. Speybroeck and S. Cottenier, Comput. Mater. Sci., 2016, 117, 390–396.
11. K. Lejaeghere, V. Van Speybroeck, G. Van Oost and S. Cottenier, Crit. Rev. Solid State Mater. Sci., 2014, 39, 1–24.
12. A. Agrawal and A. Choudhary, APL Mater., 2016, 4, 1–10.
13. O. Isayev, D. Fourches, E. N. Muratov, C. Oses, K. Rasch, A. Tropsha and S. Curtarolo, Chem. Mater., 2015, 27, 735–743.
14. A. Agrawal, P. D. Deshpande, A. Cecen, G. P. Basavarsu and A. N. Choudhary, Integrating Materials and Manufacturing Innovation, 2014, 3, 1–19.
15. R. Liu, A. Kumar, Z. Chen, A. Agrawal, V. Sundararaghavan and A. Choudhary, Sci. Rep., 2015, 5, 11551.
16. E. O. Pyzer-Knapp, G. N. Simm and A. A. Guzik, Mater. Horiz., 2016, 3, 226–233.
17. TE Design lab database is publicly available via the Citrination platform, http://www.citrination.com.
18. F. Birch, Phys. Rev., 1947, 71, 809–824.
19. F. Murnaghan, Proc. Natl. Acad. Sci. U. S. A., 1944, 30, 244–247.
20. A. Furmanchuk, A. Agrawal, J. Saal, J. Doak, G. B. Olson and A. Choudhary, ThermoEl web tool., 2016, available at: http://info.eecs.northwestern.edu/ThermoEl, accessed: 24th August 2016.
21. P. Gorai, D. Gao, B. Ortiz, S. Miller, S. A. Barnett, T. Mason, Q. Lv, V. Stevanovic and E. S. Toberer, Comput. Mater. Sci., 2016, 112, 368–376.
22. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830.
23. A. Furmanchuk, A. Agrawal, J. Saal, J. W. Doak, G. B. Olson and A. Choudhary, 2016, submitted.
24. E. Clementi and D. L. Raimondi, J. Chem. Phys., 1963, 38, 2686–2689.
25. J. C. Slater, J. Chem. Phys., 1964, 41, 3199–3204.
26. J. C. Slater, Quantum Theory of Molecules and Solids. Symmetry and Bonds in Crystals, McGraw-Hill, New York, 1965.
27. A. Zunger, in Structure and Bonding in Crystals, ed. M. O'Keeffe and A. Navrotsky, Academic Press, New York, 1981, vol. 1, p. 73.
28. P. Villars, J. Less-Common Met., 1985, 109, 93–115.
29. R. D. Shannon and C. T. Prewitt, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1969, 25, 925–946.
30. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 23, 751–761.
31. In CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton, Florida, 2003, ch. 10.
32. P. Villars and J. L. C. Daams, J. Alloys Compd., 1993, 197, 177–196.
33. G. Bergerhoff, R. Hundt, R. Sievers and I. D. Brown, J. Chem. Inf. Comput. Sci., 1983, 23, 66–69.
34. R. Rasna Thakur, R. K. Thakur and N. K. Gaur, J. Alloys Compd., 2016, 661, 257–267.
35. M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 32, 7988–7991.
36. I. R. Shein and A. L. Ivanovskii, J. Phys.: Condens. Matter, 2008, 20, 415218.
37. S. Narain, Phys. Status Solidi, 1994, 182, 273–278.
38. P. K. Lam, M. L. Cohen and G. Martinez, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 9190.
39. H. Siethoff and K. Ahlborn, Phys. Status Solidi, 1995, 190, 179–191.
40. H. Neumann, Cryst. Res. Technol., 1987, 22, 271–277.
41. H. Neumann, Cryst. Res. Technol., 1987, 22, 99–104.
42. V. Kumar, G. M. Prasad, A. R. Chetal and D. Chandra, J. Phys. Chem. Solids, 1996, 57, 503–506.
43. E. Kim and C. Chen, Phys. Lett. A, 2004, 326, 442–448.
44. D. G. Clerc, J. Phys. Chem. Solids, 1999, 60, 103–110.
45. M. Sekar, N. V. Chandra Shekar, S. Appalakondaiah, G. Shwetha, G. Vaitheeswaran and V. Kanchana, J. Alloys Compd., 2016, 654, 554–560.
46. D. Richard, L. A. Errico and M. Rentería, J. Alloys Compd., 2016, 664, 580–589.
47. K. Li, Z. Ding and D. Xue, Phys. Status Solidi B, 2011, 248, 1227–1236.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra19284j

‡ Current affiliation: Center for Health Information Partnerships, Northwestern University, Feinberg School of Medicine, Chicago, IL 60611, USA.

---