Interaction-induced energy-level crossing and transport phenomena in topological insulators†
Andrew Das Arulsamy
Condensed Matter Group, Institute of Interdisciplinary Science, No. 24, level-4, Block C, Lorong Bahagia, Pandamaran, 42000 Port Klang, Selangor DE, Malaysia. E-mail: sadwerdna@gmail.com; Tel: +60 16 9063675
First published on 28th October 2016
Abstract
A topologically insulating material, (Bi1−xSbx)2Te3 is studied in detail with respect to its resistivity measurements by evaluating these parameters—constituent chemical elements' valence states, as well as the defect types and their concentrations. Here, the ionization energy theory (IET) is exploited to unequivocally show that the electrical resistivity and carrier-type transition (n ⇌ p) for a (Bi1−xSbx)2Te3 topological insulator can be precisely captured in a consistent manner supported by experimental data. Subsequently, we expose why the insulating bulk and its topologically protected metallic surface are the two facets of the same topological insulator. In particular, these facets arise entirely from different chemical compositions and defects found in the bulk compared to its surface. Ionization energies, valence electrons and ‘special’ energy-level crossing with a finite energy gap are some of the notions that have been invoked within IET to derive the experimentally observable parameters, namely, the doping-dependent electron-ion scattering rate, resistivity and carrier-type transition. These parameters are then used to explain the experimental data obtained from (Bi1−xSbx)2Te3 and Pb1−xSnxSe compounds. In our final attempt, we use IET to unequivocally show that the topologically protected metallic surface states consist of special energy-level crossing where the crossed energy levels are not due to time reversal symmetry induced Kramers degeneracy.
1. Introduction
Degenerate energy levels (gapless) can form conducting states even if they are confined to the surface (or to the edge). If their degeneracy is kept intact against external disturbances (temperature (T), pressure, electric (E) and magnetic (B) fields), such that the bulk always has a well-defined band gap, then the materials satisfying the above conditions can be grouped into a new class of solids. These new solids are known as topological insulators (TI). At least, that is the proper and generalized definition one can think of to identify TI based on the crossed energy-level notion in two-dimensional Pancharatnam metals (with quantum Hall effects), which was first calculated by Hatsugai.1 This definition also applicable to three-dimensional TI,2,3 and it properly rules out free-electron and Fermi-liquid metals, even in the presence of a skin effect (frequency-dependent surface conductivity).4 In TI, we actually need the bulk to be gapped so that the surface states form a distinct two-dimensional system that can exhibit Pancharatnam metallic properties.5,6 This means that one may need to perform quantum Hall effect measurements5–7 to confirm whether an insulator is indeed a topological insulator because electric transport measurements,8,9 and other surface analysis techniques, such as the angle-resolved photoemission spectroscopy (ARPES),10 de Haas–van Alphen11 and Shubnikov–de Haas12 effects are insufficient to claim the bulk is gapped, while the surface is metallic, independent of the bulk.On the other hand, TI are also related to topology, a mathematical notion that deals with ‘smooth’ deformations of any entity,13 and in our case, this entity strictly refers to two-dimensional surface metallic states or degenerate energy levels. One can think of these metallic states or energy levels as the elements (or open subsets) within an open set that comprises all degenerate energy levels. This means that the energy levels or the subsets are the topology on an open set where this open set and its subsets satisfy some precise conditions, which allow smooth deformations.14 Now, any deformation to these energy levels requires one to invoke an arbitrary right-hand side (rhs) action operator13 that tacks a transition function (namely, a phase factor) on the rhs of an electronic wavefunction.15 However, it has been rediscovered recently that a wavefunction picks up or drops a phase factor as a result of a physical notion known as the Pancharatnam phase retardation (due to phase acceleration or deceleration). In fact, when the phase and (or) group momenta (μm) of a particular wavefunction changes, then one has to tack the Pancharatnam–Berry (PB) phase factor on the rhs of a wavefunction, which gives rise to the Pancharatnam wavefunction transformation16 that was originally discovered (formulated and observed) by Pancharatnam using the polarized pencil beams and Poincaré sphere.17,18 This means that, the original Berry's phase19 is a rediscovered special case (the group momentum of a wavefunction is invariant) within the generalized Pancharatnam phase.15–18 Compared to a conducting surface, the bulk requires the wavefunction to be transformed beyond the phase factor due to a nonzero energy gap between the valence and conduction bands. Therefore, the above rhs action operator has a precise physical origin within the context of quantum mechanics due to the Pancharatnam wavefunction transformation.15
Having said that, we can now set the next course of action—to understand how the definition for a topological insulator (stated in the first paragraph) can be achieved physically, or, how to identify the relevant physical parameter(s) responsible to obtain such an insulator. In this respect, Kane and Mele,20 and independently by Bernevig, Hughes and Zhang21 have confirmed the Hatsugai's surface energy-level crossing such that one needs a combination of physical properties to activate the required energy-level crossing at the edge or on the surface, while the bulk is of course, remains gapped. The physical phenomena that are at play to produce both gapped bulk and gapless surface states in a single system come from different magnitudes of certain crucial parameters (the bulk has different magnitudes compared to the edge or surface).20 For example, the interplay among these critical parameters, namely, the spin–orbit coupling, intersite hopping matrix elements, Rashba coupling and the staggered sublattice potential give rise to a topologically insulating phase.20
Note that the above critical parameters that eventually give rise to changing electronic structure in the bulk can only be different from its surface if their respective chemical composition and/or the coordination numbers are themselves different. For example, the HgTe/Hg0.3Cd0.7Te quantum wells7 for different thicknesses (d) have given rise to a quantum phase transition (QPT) from the usual gapped surface (similar to the bulk) to a gapless surface states (while the bulk is still gapped) where the critical thickness (dc) here is 6.3 nm, which refers to the width of their device. However, the existence of odd numbers of spin-polarized edge channels is actually a questionable assumption.7 Despite this, the said QPT has been correctly associated with the changing electronic structure due to spin–orbit coupling (SOC)7 following the Bernevig–Hughes–Zhang (BHZ) model.21 Here, it is acceptable to not to know exactly what other critical parameter(s) (besides SOC) are responsible for the changing electronic structure (or changing energy (Landau)-level crossing). In summary, the relation between the changing Landau-level crossing and d due to SOC originates from the changing defect types and composition or more precisely, from changing chemical composition and/or the coordination numbers with changing d. These changes due to defect types and composition will give rise to a change in SOC,22 which shall be made explicit when we discuss the doping-dependent resistivity in TI.
The point on which we do not agree with König et al.7 and BHZ21 is the assumption that time reversal symmetry (TRS) is not violated for the above device for different applied gate voltages on the basis of the BHZ model.21 This invariance of TRS in the presence of electric current (due to spin or charge or both) in any condensed matter system should not be haphazardly assumed to be true due to a well thought-out hypothesis put forth by Messiah.23 Please refer to our additional notes (prior to the Conclusions) for a proper summary. In particular, the TRS defined in ref. 23 leading to Kramers degeneracy24 is not necessarily required to obtain crossed energy levels due to interplay among the above-stated critical physical parameters. Of course, one can construct a particular Hamiltonian to satisfy TRS if the energy levels are crossed (not necessarily Dirac points due to Kramers degeneracy) between the bulk valence and conduction bands7,10,25 such that E1(k) = E2(−k) where k denotes the wavevector.26 This construction, however, does not imply that TRS is always preserved by default in the presence of an internal electric current—for example, all standard (B = 0) and Hall resistance (B ≠ 0) measurements27–29 necessarily violate TRS as a result of the nonzero internal electric current (static or time-dependent).23 For a Hall current, one needs to consider Zeeman splitting30 due to the nonzero applied magnetic field, while a static current produces a static ‘external’ magnetic (B′) field.
Therefore, our objective here is to develop the basic mechanism required to consistently explain the electronic transport phenomena and carrier-type transition in TI down to the atomic energy level. We start our analyses by invoking the properties of ionization energies and energy-level spacing within the ionization energy theory (IET), and make use of TRS results derived earlier in ref. 16. In fact, we have derived all the relevant equations required to properly understand the time reversal operation in any solid, including TI, as well as the conditions that may give rise to TRS violation in TI.16 With this knowledge as background, we will first evaluate the influence of the energy-level spacing (ξ, which is also known as the ionization energy) on resistivity and carrier-type transition with respect to different chemical compositions in (Bi1−xSbx)2Te3 and Pb1−xSnxSe. The band structure properties of (Bi1−xSbx)2Te3 and Pb1−xSnxSe relevant to understand transport phenomena have been investigated by Jinsong Zhang et al.31 and Dziawa et al.,32 respectively.
We will exploit the relation between ξ and the electron excitation probability to answer the microscopic origins for (i) the changes in doping-dependent resistivity data (including the carrier-density and electron-ion scattering magnitudes) in (Bi1−xSbx)2Te3 and Pb1−xSnxSe, and (ii) the carrier-type transition (p- to n-type or vice versa) for different chemical compositions and defects in (Bi1−xSbx)2Te3. Our research on the above-stated points ((i) and (ii)) can lead us to understand how TI fit properly and consistently within the current knowledge of atoms, metallic Fermi liquid, semiconductors, ferromagnets, Mott–Hubbard insulators, cuprate strange metals and Pancharatnam metals. In addition, these points were not addressed nor generalized in earlier reports with respect to different types of atoms, and with respect to non-Kramers degeneracy (crossed energy levels with ξ ≠ 0).
2. Ionization energy theory
Ionization energy is defined as the minimum energy required to remove a bound electron (bound to a nucleus of an atom) to infinity (r → ∞). In contrast, IET is based on the theorem that states—the minimum energy required to excite or to polarize a bound electron to a finite distance (r → rfinite) within a quantum system (atomic, molecular or solid) is proportional to the ionization energy defined above. This proportionality is precisely known as the ionization energy approximation,33,34 which can be written as,| ξquantumsystem ∝ ξconstituentatom. | (1) |
Within a quantum system, the energy is quantized and therefore, the ionization energy is also known as the energy-level spacing. This energy-level spacing can be used to rewrite the standard Schrödinger equation to read,35,36
 | (2) |
 | (3) |
2.1. Ionization energies for isolated atoms
We now list the chemical elements needed to make TI, calculate their average ionization energies and explain what these averaged values mean. For an hypothetical atom, Xi+ (with i number of valence electrons) the averaged ξ can be calculated from,
 | (4) |
| Element | Atomic number Z | Valence state | ξ /kJ mol−1 |
|---|---|---|---|
| Se | 34 | 1+ | 941 |
| Se | 2+ | 1493 | |
| Se | 4+ | 2476 | |
| Sn | 50 | 1+ | 709 |
| Sn | 2+ | 1061 | |
| Sn | 4+ | 1688 | |
| Sb | 51 | 1+ | 834 |
| Sb | 3+ | 1623 | |
| Te | 52 | 1+ | 869 |
| Te | 2+ | 1330 | |
| Te | 4+ | 2242 | |
| Pb | 82 | 1+ | 716 |
| Pb | 2+ | 1084 | |
| Pb | 4+ | 2333 | |
| Bi | 83 | 1+ | 703 |
| Bi | 3+ | 1593 |
We now briefly state the importance of approximating ξquantummatter from ξconstituentatom (ξ for short) via eqn (1) and (4). A chemical element, Xj with large ξ(Xj) means its valence electrons are not easily excited or polarized, and conversely, the electron-excitation probability and the atomic polarizability of a chemical element (Xj+1) are large if its ξ(Xj+1) is small. Furthermore, one can readily use eqn (1) to claim that the above probability and polarizability for a given TI get smaller if we systematically substitute one of its constituent chemical elements (Xj, ξ(Xj)) with another atom (Xj+1) that has a larger ξ(Xj+1). The above probability can be derived from the Fermi–Dirac statistics (FDS) with ξ as an additional restrictive condition,33,34 and is given by,
 | (5) |
 | (6) |
2.2. Relevant and irrelevant energy-level spacing
A ‘relevant’ energy-level spacing means a particular physical property is directly influenced by ξ, while an ‘irrelevant’ ξ and ξ = 0 have no influence at all. Examples of trivially relevant energy-level spacings47 are the atomic energy-level spacing,43,44 band gaps in band insulators and semiconductors,4 Mott–Hubbard gaps in Mott insulators,48 and the molecular gaps in molecules49 (between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO)). All Fermi liquid metals4 (including Pancharatnam metals28,29) require irrelevant ξ (ξirr ≠ 0),15 while ξ = 0 is for free electrons (Fermi gas).47 However, there is a special situation that can give rise to a nontrivially relevant ξ, which is applicable to strange metals in cuprates,47 and other strongly correlated metals where ξ is ‘special’ because it exists within a degenerate electronic system, and its origin is due to different wavefunctions.50 In particular, the special energy-level spacing theorem reads47,50—an electron needs energy supply to occupy another degenerate energy-level because the wavefunction representing this particular electron needs to be transformed (beyond the phase factor) to occupy the new energy-level.From our previous analyses on TRS given in ref. 16, it should be clear that TRS will be violated in the presence of static electric current regardless of whether ξ = 0, or ξ is an irrelevant constant, or ξ is a finite relevant constant. This also means that any violation of TRS does not necessarily imply a given system is gapped because the internal electric current violates TRS even in gapless systems. Apart from that, even though TRS is known to be responsible for Kramers degeneracy, TI can form non-Kramers degenerate surface states due to many other complicated interactions as pointed out in the introduction, and in ref. 47 and 50.
3. Results and discussion
We show here that the metallic property in gapless TI can be associated with the above special (nontrivially relevant) energy-level spacing (ξnontriv). Usually, a given compound is defined to be metallic if its resistivity (ρ(T)) gets smaller with lowering temperature T. Both ρ(T,x) and the carrier-type transition (n- to p-type) have been measured by Jinsong Zhang et al.31 in (Bi1−xSbx)2Te3. Apart from metallic resistivity, we will also explain why the bandgap of another TI, namely, Pb1−xSnxSe changes with Sn substitution, which were first measured by Strauss51 and later confirmed by Dziawa et al.32 using ARPES measurements. The latter bandgap analyses are based on the trivially relevant ξtriv. Since the energy-level spacing for both gapless and gapped systems are nonzero and relevant, we are therefore forced to identify them with ξnontriv and ξtriv for the gapless and gapped systems, respectively.3.1. Carrier density and electron–ion interaction
Changes in the magnitude of resistivity in TI or any other strongly correlated solid state systems are usually due to doping x, T and B. In the absence of B, and for constant T, the microscopic physical parameters that will significantly influence the resistivity with respect to x are the carrier density (n(ξ)) and the scattering amplitude, |f(θ)|. Here,34,45| n(ξ) = C(T)exp[λ(ξ − E0F)], | (7) |
 | (8) |
To understand why τ(x)e:ion−1 ∝ |f(θ)|, we use the Born approximation52 and the renormalized screened Coulomb potential,45
 | (9) |
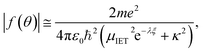 | (10) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |f(θ)|. As a consequence, the approximate resistivity can be written in the form (using eqn (8)),
|f(θ)|. As a consequence, the approximate resistivity can be written in the form (using eqn (8)),
 | (11) |
Thus far, we have ignored the T-dependence even though we know both ξ(T) and τe:ion(T) do exist simply because their explicit forms are unknown due to their complex T-dependences. Logically, τe:ion has to be T-dependent, while ξ has been experimentally proven to be T-dependent by Dionicio53 using the results of Fukuda et al.54 In particular, Dionicio showed that the valence state of a given multivalent chemical element is T-dependent. Despite this, eqn (11) is exact with respect to ξ-dependence, and therefore, it is sufficient for our analyses, and to show that indeed non-Kramers degeneracy (due to relevant ξnontriv ≠ 0) is responsible for the metallic surface states in TI.
It is also worth noting here that one can indeed use the lattice-strain parameter (that can be estimated by calculating the changes in the Raman phonon frequency and intensity) to evaluate defects and their concentrations in topological insulators or any solids, but this information is limited to the study of defects per se, which cannot be directly exploited to examine the carrier-type transition and resistivity. Moreover, by working within IET, we do not need to assess the strength of the lattice-strain and its distribution because the energy-level spacing is far more fundamental than all other macroscopic entities, which can be applied to model and theorize many physical parameters and mechanisms as proven in ref. 16. As a matter of fact, we can also exploit IET to calculate the changes to the Raman phonons as a result of defects and doping.
3.2. Doping-dependent resistivity and carrier-type transition
We have concluded the derivation of all the equations needed to explain the measured resistivity data and the carrier-type transition in Pb1−xSnxSe and (Bi1−xSbx)2Te3. Dziawa et al.32 have studied the narrow bandgap semiconductor, Pb1−xSnxSe where a topological phase transition is observed for x = 0.23 when T is reduced from 300 K to 77 K. In particular, Pb0.77Sn0.23Se is a gapped semiconductor for T = 300 K, and it becomes a gapless TI for T = 77 K due to band inversion observed indirectly via ARPES. Moreover, for a given T (300 K or 195 K or 77 K), Sn substitutional doping (increasing x from 0 to about 0.3) systematically reduces the bandgap of the Pb1−xSnxSe semiconductor from about 0.3 to approximately 0.05 eV (see Fig. 1 in ref. 32). This observation is easily understood within IET by noting that ξ now represents the bandgap, ξSn2+ < ξPb2+ (see Table 1), and from eqn (7) and (11), ρ(x) is predicted to decrease with increasing Sn content, provided that the valence states of the chemical elements (Pb and Sn) do not change significantly due to defects. If the valence states do change, then the analyses become tedious, which have been addressed elsewhere for other strongly correlated materials and oxides22,47,55 where topological insulators are no exception (see below).In the absence of defects, the changes in ρ(x) for Pb1−xSnxSe have been exposed in a straightforward manner within IET. However, the (Bi1−xSbx)2Te3 material is reported to have a complicated doping-dependent resistivity by Jinsong Zhang et al.31 For example, the measured ρ(x) first increases with x, for up to x = 0.94, and then it reduces until x = 1 (see Fig. 4 in ref. 31). With increasing Sb content (0 ≤ x ≤ 0.94), the system also becomes relatively more insulating. Further Sb substitutional doping (0.94 < x ≤ 1) leads to a weaker insulating behavior such that Sb2Te3 is a semi-metal with holes as the dominant charge carriers. In contrast, Bi2Te3 is an electron-dominant metal. The above carrier-type transition from an n-type insulator to a p-type semi-metal are of course due to defects where the valence states for Sb3+ and Te2+ are not constant with doping (for x > 0.94).
Similar to Si = [Si4+][Si4+] semiconductor, (Bi1−xSbx)2Te3 is also predominantly covalent bonded and therefore, we can also write it in the form, [(Bi1−xSbx)2]6+[Te3]6+ = [(Bi1−x3+Sbx3+)2][Te32+]. Using eqn (7) and (11), and the fact that ξBi3+ < ξSb3+, one can deduce that ρ(x) should increase with increasing Sb content, which has been observed for 0 ≤ x ≤ 0.94. Next, to understand the carrier-type transition in this class of material, it is sufficient for us to focus on these two extreme cases, namely, for x = 0 (n-type; Bi23+Te32+) and for x = 1 (p-type; Sb23+Te32+). We will exploit the carrier-type transition theorem developed in ref. 55, which will also lead us to understand why ρ(x) has decreased for x > 0.94.
The carrier-type transition theorem states that p-type materials with relevant ξ should satisfy this condition,55
| ξacceptora+ < ξhosth+, a < h and xacceptor < yhost, | (12) |
However, Sb23+Te32+ can be made to be a p-type material if we introduce a small amount of defects (with xnew ≪ 2 and y ≪ 3) to give rise to [Sb2−xnew3+Sbxnewa′+][Te3−y2+Teya′′+]. Here, if xnew exists, then y should also exist to balance the defects introduced by xnew so as to maintain a proper coordination number, regardless of the crystal growth conditions because the distribution of these defects need not be homogeneous at all. We now evaluate [Sb2−xnew3+Sbxnewa′+] and [Te3−y2+Teya′′+] separately. It is apparent that Sb2−xnew3+ is the host and Sbxnewa′+ is the acceptor where ξSb3+ > ξSba′+ if a′ < 3+. Similarly, for [Te3−y2+Teya′′+], Te3−y2+ is the host, while Teya′′+ is the acceptor such that ξTe2+ > ξTea′′+ if a′′ < 2+. These inequalities satisfy eqn (12), and consequently, Sb2−xnew3+Sbxnewa′+Te3−y2+Teya′′+ is a p-type TI in the presence of defects.
Moreover, ξSb3+ > ξSba′+ and ξTe2+ > ξTea′′+ give rise to decreasing ρ(x) for x > 0.94, which is in agreement with the observed data (see Fig. 4 in ref. 31 and Fig. 1(a) and (b)). The resistivity should decrease for x > 0.94 because the carrier-type transition to p-type is caused by the increasing defect density (xnew and y), namely, Sba′+ and Tea′′+ for x > 0.94, which give rise to an increasing number of holes due to these inequalities, ξSb3+ > ξSba′+ and ξTe2+ > ξTea′′+. Using the above analyses, one can also obtain theoretically a p-type Bi23+Te32+ with appropriate defects, Bia′+ and Tea′′+ where a′ < 3+ and a′′ < 2+. The above defect densities can be determined experimentally by using the chemical method to measure the valence states of various chemical elements that was first carried out by Mahendiran et al.56
 | ||
Fig. 1 (a) Sheet resistance, R□ at 300 K for x = 0, 0.5, 0.75, 0.88, 0.94. (b) The same resistance for x = 0.94, 0.96, 0.98, 1.0. The data points in both (a) and (b) were obtained from ref. 31 for (Bi1−xSbx)2Te3 topological insulator. The calculated curves follow the doping-dependent resistivity model, R□ = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[Bλξ(x)] where A and B (dimensionless) are doping-independent constants, while x and λ denote doping and IET fundamental constants, respectively and ξ(x) is the doping-dependent energy-level spacing, which is not a constant because ξ(x) varies when x varies. Hence, the fitting is trivial. This model is a simplified version from IET (see eqn (11)). The curve in (a) increases with x because ξ(x) = (1 − x)ξ(Bi3+) + (x)ξ(Sb3+) where ξ(Bi3+) < ξ(Sb3+). The curve in (b) however, reduces with doping x > 0.94 because of defects (due to the existence of Sba′+ and Tea′′+) such that ξSb3+ > ξSba′+ and ξTe2+ > ξTea′′+. The said defects have led us to write, ξ(x) = (2 − xnew)ξSb3+ + (xnew)ξSba′+ + (3 − y)ξTe2+ + (y)ξTea′′+, which means, R□ becomes smaller for x > 0.94 due to the contributions made by Sba′+ and Tea′′+ ions. The above inequalities for the curve in (b) explain why R□ reduces for x > 0.94 and also why there is a carrier-type transition from n- to p-type (see text for details). exp[Bλξ(x)] where A and B (dimensionless) are doping-independent constants, while x and λ denote doping and IET fundamental constants, respectively and ξ(x) is the doping-dependent energy-level spacing, which is not a constant because ξ(x) varies when x varies. Hence, the fitting is trivial. This model is a simplified version from IET (see eqn (11)). The curve in (a) increases with x because ξ(x) = (1 − x)ξ(Bi3+) + (x)ξ(Sb3+) where ξ(Bi3+) < ξ(Sb3+). The curve in (b) however, reduces with doping x > 0.94 because of defects (due to the existence of Sba′+ and Tea′′+) such that ξSb3+ > ξSba′+ and ξTe2+ > ξTea′′+. The said defects have led us to write, ξ(x) = (2 − xnew)ξSb3+ + (xnew)ξSba′+ + (3 − y)ξTe2+ + (y)ξTea′′+, which means, R□ becomes smaller for x > 0.94 due to the contributions made by Sba′+ and Tea′′+ ions. The above inequalities for the curve in (b) explain why R□ reduces for x > 0.94 and also why there is a carrier-type transition from n- to p-type (see text for details). | ||
In summary, both Sb23+Te32+ and Bi23+Te32+ can be synthesized as p-type materials for xnew ≠ 0 and y = 0 or xnew = 0 and y ≠ 0, without requiring both xnew ≠ 0 and y ≠ 0 as discussed above. We also have used the so-called relevant ξ to explain the transport properties (in (Bi1−xSbx)2Te3 and Pb1−xSnxSe) and the n- to p-type carrier-type transition in (Bi1−xSbx)2Te3, which unequivocally prove that Kramers degeneracy is not responsible for the metallic surface states, at least in the above stated TI.
4. Additional notes
We have justified that these topological insulators, namely, (Bi1−xSbx)2Te3 and Pb1−xSnxSe, in the presence of surface electric current necessarily violate TRS. Even in the absence of IET, TRS is guaranteed to be violated for any solid state system (gapless or gapped) in the presence of electric current.16 Furthermore, within IET, we have postulated that the degeneracy in topological insulators is not of the Kramers-type. To prove this postulate, we derived the temperature-independent resistivity and scattering-rate equations as functions of doping (x). The experimental results obtained from the above materials ((Bi1−xSbx)2Te3 and Pb1−xSnxSe) follow exactly as predicted by these equations (eqn (11) and (12)). This means that, the energy levels are crossed (in gapless systems) in such a way that there are nonzero wavefunction-induced energy gaps at the crossing points. This ‘special’ gap exists due to different orthogonalized wavefunctions.To reinforce the above non-Kramers degeneracy in topological insulators, we also provide precise explanation on the physics of n- to p-type carrier-type transition in (Bi1−xSbx)2Te3. As a matter of fact, the existence of non-Kramers degeneracy in any system, correlated or not, is not surprising because complicated interactions and/or their interplay indeed have given rise to crossed energy levels. For example, in Fermi metals, metallic heavy fermions, conventional superconductors, strange metals (cuprates and other strongly correlated metals), metallic ferromagnets (manganites), Pancharatnam metals (2-dimensional Fermi gas) and semi-metals.
We have made use of the fact that with or without Kramers degeneracy, TRS will be violated in the presence of spinful electric current,16 which directly challenges the analysis carried out by König et al.7 and Bernevig, Hughes and Zhang.21 They7,21 claimed that the spin-down and spin-up (spin polarized) edge currents do not violate TRS due to Kramers degeneracy. Secondly, the degeneracy in topological insulators is not of the Kramers-type, which are unambiguously supported by the doping-dependent carrier-type transition and resistivity data.
In summary, interacting topological insulators, namely, (Bi1−xSbx)2Te3 and Pb1−xSnxSe cannot be understood in terms of noninteracting electrons. Even though the edge states of noninteracting or interacting topological insulators can be protected by constructing a time reversal invariant (TRI) Hamiltonian, this Hamiltonian ceases to be valid for ξnontriv ≠ 0. In particular, it is true that a state with current breaks TRS, and this violation is not going to make the Hamiltonian break its time reversal operation. However, the gapped-degeneracy condition, ξnontriv ≠ 0, which is also known as the special gap, is the one that has been shown to break TRS of a TRI Hamiltonian. In other words, TRI Hamiltonian is incompatible for interacting topological insulators with ξnontriv ≠ 0. Note that the time reversal operation of this Hamiltonian can only stay intact if it represents a noninteracting topological insulator such that the said insulator obeys the gapless-degeneracy condition, ξirr ≠ 0 or ξ = 0.
5. Conclusions
We have derived the temperature-independent resistivity and scattering-rate equations as functions of doping (x) supported by the experimental results obtained from these topological insulators, (Bi1−xSbx)2Te3 and Pb1−xSnxSe. The experimental doping-dependent resistivity data follow exactly as predicted by eqn (11). Apart from that, the n- to p-type transition observed in (Bi1−xSbx)2Te3 has also been explained in a consistent manner using the ionization energy theory on the basis of eqn (12).First, we have correctly determined the microscopic physics responsible for the systematic changes to the band gap and the resistivity in Pb1−xSnxSe where the said changes are due to changing the energy-level spacing (ξ) that controls the density of valence electrons. Subsequently, by introducing relevant defects to invoke the possibility of different valence states for a given chemical element, we then moved on to explain the physics responsible for the n- to p-type carrier-type transition and doping-dependent (temperature-independent) resistivity curves in (Bi1−xSbx)2Te3 compound.
We can extend our conclusions stated above to find the origin of the topologically protected metallic surface states from the insulating bulk material. In particular, by varying the chemical composition (x) on the surface of an insulator, we have actually introduced significant amount of defects on the surface, leading to the said metallic surface. These defects have permitted us to invoke the changes in the valence states of the constituent chemical elements on the surface of the (Bi1−xSbx)2Te3 topological insulator. We have found that these changes in the valence states for different doping, x, on the surface are responsible for (i) the n- to p-type carrier-type transition, and (ii) the existence of topologically protected metallic states on the surface such that the bulk remains insulating. Therefore, the bulk has remained insulating due to the fact that the defect and the chemical composition in the bulk have effectively stayed intact with doping compared to its surface. In other words, if the chemical composition and defects have remained unchanged with doping, then we cannot produce two physically distinctive features, namely, the insulating bulk and the topologically protected metallic surface. Conversely, to produce a topological insulator, we need to introduce sufficient amount of defects by changing the chemical composition on the surface of an insulator. Using the ionization energy theory, we have provided the precise chemico-physical analysis required to explain the observed doping-dependent resistivity and carrier-type transition for (Bi1−xSbx)2Te3.
The above conclusions that have been derived from the transport and carrier-type transition analysis automatically rule out the existence of time-reversal symmetry-induced Kramers degeneracy in (Bi1−xSbx)2Te3. For example, we have exploited the interaction induced crossed energy levels within IET to explain the transport properties and the n- to p-type carrier-type transition consistently, in the absence of Kramers degeneracy. In doing so, we have established that the nontrivially relevant ξ played a pivotal role in the metallic states of topological insulators where Kramers degeneracy is not required to capture the gapless metallic surface states due to nonzero and relevant ξ.
Acknowledgements
I am grateful to the financiers, Sebastiammal Savarimuthu, Arulsamy Innasimuthu, Amelia Das Anthony, Malcolm Anandraj and Kingston Kisshenraj for their kind support and hospitality between Aug 2011 and Aug 2013. I am also grateful to Marco Fronzi (Tyndall National Institute, Ireland) for his unconditional help in providing most of the references. I thank the referee for pointing out the missing explanation on the violation of TRI Hamiltonian.References
- Y. Hatsugai, Phys. Rev. Lett., 1993, 71, 3697 CrossRef CAS PubMed.
- L. Fu, C. L. Kane and E. J. Mele, Phys. Rev. Lett., 2007, 98, 106803 CrossRef PubMed.
- J. E. Moore and L. Balents, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 121306 CrossRef.
- N. W. Ashcroft and N. D. Mermin, Solid State Physics, Rinehart and Winston, New York, Holt, 1976 Search PubMed.
- R. Yu, W. Zhang, H. J. Zhang, S. C. Zhang, X. Dai and Z. Fan, Science, 2010, 329, 61 CrossRef CAS PubMed.
- C. Z. Chang, J. Zhang, X. Feng, J. Shen, Z. Zhang, M. Guo, K. Li, Y. Ou, P. Wei, L. L. Wang, Z. Q Ji, Y. Feng, S. Ji, X. Chen, J. Jia, X. Dai, Z. Fang, S. C. Zhang, K. He, Y. Wang, L. Lu, X. C. Ma and Q. K. Xue, Science, 2013, 340, 167 CrossRef CAS PubMed.
- M. König, S. Wiedmann, C. Brüne, A. Roth, H. Buhmann, L. W. Molenkamp, X. L. Qi and S. C. Zhang, Science, 2007, 318, 766 CrossRef PubMed.
- S. Barua and K. P. Rajeev, AIP Adv., 2014, 4, 017135 CrossRef.
- K. von Klitzing and G. Landwehr, Solid State Commun., 1971, 9, 2201 CrossRef CAS.
- Y. L. Chen, J. H. Chu, J. G. Analytis, Z. K. Liu, K. Igarashi, H. H. Kuo, X. L. Qi, S. K. Mo, R. G. Moore, D. H. Lu, M. Hashimoto, T. Sasagawa, S. C. Zhang, I. R. Fisher, Z. Hussain and Z. X. Shen, Science, 2010, 329, 659 CrossRef CAS PubMed.
- C. Kittel, Introduction to Solid State Physics, Wiley, New York, 1976 Search PubMed.
- L. W. Schubnikov and W. J. de Haas, Proc. R. Neth. Acad. Arts Sci.: Nat. Sci., 1930, 33, 130 Search PubMed.
- M. Nakahara, Geometry, Topology and Physics, IOP Publishing, Bristol, 2003 Search PubMed.
- R. Geroch, Mathematical Physics, University of Chicago Press, Chicago, 1985 Search PubMed.
- A. D. Arulsamy, Pramana, 2015, 85, 161 CrossRef.
- A. D. Arulsamy, Ionization Energy Theory: Formalism, CreateSpace, Seattle, 2016, vol. I Search PubMed.
- S. Pancharatnam, Proc. - Indian Acad. Sci., Sect. A, 1956, 44, 427 Search PubMed.
- S. Pancharatnam, Collected Works of Shivaramakrishnan Pancharatnam, Oxford, Oxford University Press, 1975 Search PubMed.
- M. V. Berry, Proc. R. Soc. London, Ser. A, 1984, 392, 45 CrossRef.
- C. L. Kane and E. J. Mele, Phys. Rev. Lett., 2005, 95, 146802 CrossRef CAS PubMed.
- B. A. Bernevig, T. L. Hughes and S. C. Zhang, Science, 2006, 314, 1757 CrossRef CAS PubMed.
- A. D. Arulsamy, X. Y. Cui, C. Stampfl and K. Ratnavelu, Phys. Status Solidi B, 2009, 246, 1060 CrossRef.
- A. Messiah, Quantum Mechanics, Dover Pub. Inc., New York, 1999, ch. XV, p. 664 Search PubMed.
- H. A. Kramers, Proc. Amsterdam Acad., 1930, 33, 959 CAS.
- M. Z. Hasan and C. L. Kane, Rev. Mod. Phys., 2010, 82, 3045 CrossRef CAS.
- R. Roy, Phys. Rev. B: Condens. Matter Mater.Phys., 2009, 79, 195321 CrossRef.
- E. H. Hall, Philos. Mag., Ser. 5, 1881, 12, 157 CrossRef.
- K. von Klitzing, G. Dorda and M. Pepper, Phys. Rev. Lett., 1980, 45, 494 CrossRef CAS.
- D. C. Tsui, H. L. Stormer and A. C. Gossard, Phys. Rev. Lett., 1982, 48, 1559 CrossRef CAS.
- P. Zeeman, Philos. Mag., 1897, 43, 226 Search PubMed.
- J. Zhang, C. Z. Chang, Z. Zhang, J. Wen, X. Feng, K. Li, M. Liu, K. He, L. Wang, X. Chen, Q. K. Xue, X. Ma and Y. Wang, Nat. Commun., 2011, 2, 1 Search PubMed.
- P. Dziawa, B. J. Kowalski, K. Dybko, R. Buczko, A. Szczerbakow, M. Szot, E. Lusakowska, T. Balasubramanian, B. M. Wojek, M. H Berntsen, O. Tjernberg and T. Story, Nat. Mater., 2012, 11, 1023 CAS.
- A. D. Arulsamy, Phys. C, 2001, 356, 62 CrossRef CAS.
- A. D. Arulsamy, Phys. Lett. A, 2002, 300, 691 CrossRef.
- A. D. Arulsamy, Pramana, 2010, 74, 615 CrossRef.
- A. D. Arulsamy, Ann. Phys., 2011, 326, 541 Search PubMed.
- A. D. Arulsamy, Indian J. Phys., 2014, 88, 609 CrossRef CAS.
- A. D. Arulsamy, RSC Adv., 2016, 6, 52082 RSC.
- A. D. Arulsamy, J. Earth Syst. Sci., 2015, 124, 683 CrossRef.
- R. Shankar, Rev. Mod. Phys., 1994, 66, 129 CrossRef.
- R. Shankar, Phys. A, 1991, 177, 530 CrossRef.
- R. Shankar, Philos. Trans. R. Soc. London, Ser. A, 2011, 369, 2612 CrossRef CAS PubMed.
- Y. Ralchenko, A. E. Kramida and J. Reader, 2013, http://physics.nist.gov/asd3.
- M. J. Winter, 2013, http://www.webelements.com.
- A. D. Arulsamy, Phys. Lett. A, 2005, 334, 413 CrossRef.
- A. D. Arulsamy and K. Ostrikov, Phys. Lett. A, 2009, 373, 2267 CrossRef.
- A. D. Arulsamy, J. Supercond. Novel Magn., 2014, 27, 309 CrossRef CAS.
- N. F. Mott, Rev. Mod. Phys., 1968, 40, 677 CrossRef CAS.
- I. N. Levine, Quantum Chemistry, Prentice-Hall, New Jersey, 2000 Search PubMed.
- A. D. Arulsamy, Prog. Theor. Phys., 2011, 126, 577 CrossRef.
- A. J. Strauss, Phys. Rev., 1967, 157, 608 CrossRef CAS.
- D. J. Griffiths, Introduction to Quantum Mechanics, Prentice-Hall, New Jersey, 2005 Search PubMed.
- G. A. Dionicio, Electrical resistivity of YbRh2Si2 and EuT2Ge2 (T = Co, Cu) at extreme conditions of pressure and temperature, PhD thesis, Technical University of Dresden, Dresden, 2006.
- S. Fukuda, Y. Nakanuma, J. Sakurai, A. Mitsuda, Y. Isikawa, F. Ishikawa, T. Goto and T. Yamamoto, J. Phys. Soc. Jpn., 2003, 72, 3189 CrossRef CAS.
- A. D. Arulsamy, K. Eleršič, M. Modic, U. Cvelbar and M. Mozetič, ChemPhysChem, 2010, 11, 3704 CrossRef CAS PubMed.
- R. Mahendiran, S. K. Tiwary, A. K. Raychaudhuri, T. V. Ramakrishnan, R. Mahesh, N. Rangavittal and C. N. R. Rao, Phys. Rev. B: Condens. Matter, 1996, 53, 3348 CrossRef CAS.
Footnote |
| † PACS no. 72.10.Bg; 72.20.Dp. |
| This journal is © The Royal Society of Chemistry 2016 |
