Optimization of protein loaded PLGA nanoparticle manufacturing parameters following a quality-by-design approach

Abstract

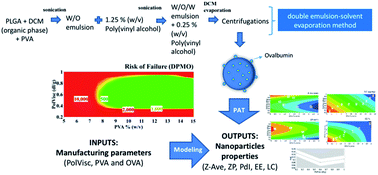
This paper discusses the development of a multivariate-based regression model for estimating the critical attributes to establish a design-space for poly(lactic-co-glycolic acid) (PLGA) nanoparticles formulated by a double emulsion–solvent evaporation method. A three-level, full factorial experimental design is used to assess the impact of three different manufacturing conditions (polymer viscosity, surfactant concentration and amount of model antigen ovalbumin) on five critical particle attributes (zeta potential, polydispersity index, hydrodynamic diameter, loading capacity and entrapment efficiency). The optimized formulation was achieved with a viscosity of 0.6 dl g⁻¹, a surfactant concentration of 11% (w/v) in the internal phase and 2.5% (w/w) of ovalbumin. The design-space that is satisfied for nanoparticles with the targeted attributes was obtained with a polymer viscosity between 0.4 and 0.9 dl g⁻¹, a surfactant concentration ranging from 8 to 15% (w/v) and 2.5% (w/w) of ovalbumin. The nanoparticles were spherical and homogenous and were extensively taken up by JAWS II murine immature dendritic cells without affecting the viability of these phagocytic cells. Better understanding was achieved by multivariate regression to control process manufacturing to optimize PLGA nanoparticle formulation. Utilization of multivariate regression with a defined control space is a good tool to meet product specifications, particularly over a narrow variation range.

---

Introduction

Nanotechnology has become increasingly important during the last two decades, especially in biomedical and health sciences, where it is used for the prevention, diagnosis and treatment of disease.¹ Much effort is focused on producing nanosystems to protect loaded pharmaceutically active molecules from systemic degradation and to target specific tissues and cells. It thus becomes possible to achieve higher therapeutic levels at lower doses, thus reducing off-target toxicity profiles. Submissions of nanomedicines to the regulatory agencies have also increased as more has become known about these complex medicines.² However, from 1994 to 2013 there was an average of only two nanomedicines accepted per year by the European Medicines Agency (EMA), mostly due to late stage clinical trial failures.^3,4

Nanomedicines are often considered to be complicated systems compared to traditional medicines. The manufacture of nanomedicines is acutely reliant on process optimization. Raw materials and multiple process factors influence their physicochemical properties that then impact biological performance.^2,5 Unfortunately, most nanomedicines are developed empirically without any deep understanding of process–property relations, and not taking into account the challenges for scaling the production process of the best candidates.^5–8 The scale-up of laboratory developed processes for nanomedicine fabrication is complex as minor variations often cause loss of stability and reduce biological activity.²

While early collaboration between academia and the pharmaceutical industry is important,⁹ it becomes more and more important to investigate the process–nanomedicine relationships at preclinical stages fastening the clinical development.

For all these reasons, the US Food and Drug Administration (FDA) recommends the use of the Quality by Design (QbD) approach for the rational design of nanomedicines to preserve drug product quality.² QbD is one of today's critical topics concerning new pharmaceuticals manufacturing process development, as described in the International Conference on Harmonization guideline Q8 (R2)-Pharmaceutical.¹⁰ QbD involves defining critical quality attributes (CQAs) of pharmaceuticals and critical process parameters (CPPs) together with the establishment of relations between these properties aiming at defining a range within the CPPs space leading to drug product specifications compliance. Drug product specifications are based on the desired efficacy and safety (drug performance) characteristics and will be part of a risk-based quality control strategy. The CPPs optimal region is called the design-space.¹¹ A common methodology for understanding the relationships between CPPs and CQA explores design of experiments (DoE) strategies coupled with multivariate data analysis methods.¹²

The DoE approach to conduct experiments minimizes the workload and amount of required materials, due to the simultaneous variation of several factors and consequent evaluation of their combined effect on CQAs.¹³ DoE has been applied in the optimization of the formulation of different nanosystems, including metallic,^14,15 lipid,^16,17 and polymeric nanoparticles.^18,19

Poly(lactic-co-glycolic acid) (PLGA) is one of the most explored biocompatible and biodegradable synthetic polymers for the delivery of multiple bioactive molecules, being a component of medicines already approved by FDA and EMA for parenteral administration in humans.²⁰ This is the most studied biomaterial for drug delivery, presenting particularly attractive mechanical properties and tunable degradation rates, suitable for the release of the desired dose and release interval of hydrophilic and hydrophobic molecules.²¹ However, the manufacturing process of PLGA nanoparticles on a current good manufacturing practice (GMP) compliant environment is not easy or economically attractive. In fact, several laboratory steps typically used for making PLGA nanoparticles (e.g. ultracentrifugation or sonication) cannot be easily scaled-up.²⁰ Additionally, encapsulation of proteins in PLGA nanoparticles is often problematic especially when the most used water-in-oil-in-water (w/o/w) double emulsion–solvent evaporation procedure is adopted.²²

This work explores the development of a multivariate regression model for estimating CQAs of PLGA nanoparticles for vaccine delivery prepared by the double emulsion–solvent evaporation method,²³ aiming at defining a design-space. The adopted methodology relies on a DoE for the evaluation of the impact of different product-related manufacturing conditions (polymer viscosity (PolVisc), surfactant concentration (PVA) and amount of model antigen ovalbumin (OVA)) on zeta potential (ZP), polydispersity index (PdI), hydrodynamic diameter (Z-ave), loading capacity (LC) and entrapment efficiency (EE).

To the best of our knowledge this is the first time that this set of CPPs (PolVisc, PVA and OVA) was evaluated applying a QbD approach for the manufacturing of nanoparticles. In the literature, studies describing DoE approaches to control manufacturing processes of polymeric nanosystems are in fact in limited number, and only a few of those established a design-space. Moreover, the use of DoE software in this context has been reported only once by Choisnard et al. (2005) to control the size of amphiphilic cyclodextrin nanoparticles.²⁴

Results and discussion

Models

Models were fitted considering experiments produced according to the DoE (Table 1).

Table 1 Experimental design table and experimental results

Exp.	Factors			Responses
	PVA (%)	PolVisc (dl g^−1)	OVA (%)	Z-ave (nm)	PdI	ZP (mV)	EE (%)	LC (μg mg^−1)
a Results not shown since this experiment was excluded from the analysis.
1	5.0	1.0	0.0	239.9	0.109	−2.17	0.000	0.000
2	5.0	1.0	2.5	233.0	0.188	−3.06	76.72	19.18
3	5.0	1.0	5.0	204.3	0.103	−2.88	47.49	23.74
4	10	1.0	0.0	212.5	0.079	−3.35	0.000	0.000
5	10	1.0	2.5	210.7	0.141	−2.71	56.09	14.02
6	10	1.0	5.0	206.5	0.086	−2.72	49.97	24.98
7	15	1.0	0.0	228.2	0.079	−2.90	0.000	0.000
8	15	1.0	2.5	216.3	0.096	−2.95	45.83	11.46
9	15	1.0	5.0	207.2	0.062	−3.94	49.50	24.75
10	5.0	0.2	0.0	210.8	0.192	−2.74	0.000	0.000
11	5.0	0.2	2.5	214.2	0.177	−2.66	86.62	21.65
12	5.0	0.2	5.0	187.9	0.076	−4.24	51.33	12.83
13	10	0.2	0.0	224.6	0.213	−3.07	0.000	0.000
14	10	0.2	2.5	191.6	0.158	−3.11	83.63	20.91
15	10	0.2	2.5	191.9	0.110	−2.73	88.38	22.10
16	10	0.2	2.5	192.9	0.107	−3.80	85.42	21.36
17	10	0.2	2.5	198.9	0.106	−2.88	49.01	12.25
18	10	0.2	5.0	191.4	0.153	−4.24	56.35	14.09
19	15	0.2	0.0	210.5	0.175	−3.44	0.000	0.000
20	15	0.2	2.5	209.2	0.177	−2.94	39.42	9.860
21	15	0.2	5.0	^a	^a	^a	^a	^a
22	5.0	0.6	0.0	209	0.061	−2.29	0.000	0.000
23	5.0	0.6	2.5	196.7	0.043	−3.38	83.44	20.86
24	5.0	0.6	5.0	196.8	0.125	−2.9	12.96	3.240
25	10	0.6	0.0	194.6	0.055	−2.39	0.000	0.000
26	10	0.6	2.5	197.2	0.086	−3.73	37.35	9.340
27	10	0.6	5.0	191.5	0.057	−3.05	33.67	8.420
28	15	0.6	0.0	189.5	0.070	−2.54	0.000	0.000
29	15	0.6	2.5	203.8	0.115	−1.07	35.62	8.900
30	15	0.6	5.0	188.1	0.103	−2.58	19.43	4.860

---

Before any modeling attempt, data from all experiments were subjected to an outlier test to avoid unwanted effect of incoherent experiments in models. Principal components analysis (PCA) is a recommended method for the detection of outliers on multivariate data.²⁵ Data from the 30 experiments were modeled by PCA (auto-scaled data) and three principal components were retained encompassing 91.8% of the total data variance. Both Hotelling's T² and squared prediction error statistics signalled experiment 21 as an outlier, as the factors used in this experiment (15% (w/v) PVA, 0.2 dl g⁻¹ PolVisc, 5% (w/w) OVA) led to unstable nanoparticles. In consequence, this experiment was excluded from further processing.

All models considered initially a structure encompassing single, interactions and squared terms. Each response model was pruned by excluding statistically non-significant terms considering a significance level of 0.05. Terms were removed one-by-one sequentially until no statistically non-significant terms were present or until a reduction on the regression Q² was observed (Table 2).

Table 2 Models' coefficients^a and performance indicators

Coefficients	Z-ave (nm)	PdI	ZP (mV)	EE (%)	LC (μg mg^−1)
a All coefficients are statistically significant for a significance level of 0.05.
Offset	191.9	0.080	−2.660	63.96	15.52
PVA	−2.560	—	—	−20.99	−3.240
PolVisc	7.520	−0.020	0.160	—	−1.880
OVA	−8.450	—	−0.290	−23.94	−2.230
PVA^2	6.640	—	—	—	—
PolVisc^2	13.75	0.050	−0.470	—	—
PVA*OVA	—	—	—	20.42	—
PolVisc*OVA	—	—	—	—	9.180
Regression p-value	<0.001	0.001	0.043	0.004	0.086
RMSE	7.2	0.036	0.540	14.90	5.180
RER	7.2	4.700	5.800	5.100	4.200

---

Presented model coefficients were scaled back to original units. The interpretation of the non-dimensional RER parameter normally considers that values above 10 are indications of models with very good accuracy, while values between 5 and 10 are acceptable models, and below 5 are considered models with poor accuracy. Results demonstrate that most models yielded RER values between 5 and 10, which is an indication that average accurate models were obtained. Note that all regressions are statistically significant at a significance level of 0.05 (p-values below 0.05), except the regression for LC with a p-value of 0.086. This was in fact the lowest RER value that was obtained for this attribute. The lack-of-fit test for all models revealed a p-value above 0.05 indicating good reproducibility (data not shown).

The obtained PLGA nanoparticles' Z-ave ranged from 187.9 to 239.9 nm. Model for this attribute involved all single terms, together with squared terms for PVA (positive) and PolVisc (positive). The effects of PolVisc and OVA can be observed on the contour plot of Fig. 1A, showing that a minimum nanoparticles' Z-ave (185 nm) can be achieved using a PolVis in the interval 0.3 to 0.6 dl g⁻¹, for values ranging from 4.2 to 5.0% (w/w) of OVA. A PLGA polymer with viscosity outside this range in addition to a lower OVA leads to higher Z-ave values.

Fig. 1 Contour plot showing the influence of OVA and PolVisc on (A) Z-ave and (B) ZP (simulation considering PVA = 10%).

Yerlikaya et al. (2013) also studied the effect of surfactant concentration in aqueous phase (%) on Z-ave, ZP and EE of paclitaxel-loaded PLGA nanoparticles.²⁶ The authors also followed a QbD approach, but an incomplete factorial design was employed (Plackett–Burman design and Box–Behnke design).²⁶ Regarding Z-ave response, the surfactant concentration on aqueous phase was considered one of the most significant factors affecting this QCA (p-value = 0.026, Plackett–Burman).²⁶ In our Z-ave model, PVA was not the most important factor (p-value = 0.21), but it was observed that an increase in PVA in the internal aqueous phase, decreased PLGA nanoparticles Z-ave. This fact was also observed by Rahman et al. (2010) and it was indeed expected due to the higher emulsifier activity that prevents droplets' coalescence.^27,28

In our study, the square of PVA (p-value = 0.045) was statistically more significant than simply the PVA factor. However, it is not possible to compare with Yerlikaya's work, because Plackett–Burman design is not intended to evaluate factors' interaction. In our study, the PolVisc was the factor that had major influence on the Z-ave response (p-value = 0.0005). This may be related with the higher viscosity of the organic phase that could have reduced the sonication efficiency. According to Rahman et al. (2010) higher Z-ave was obtained with an increase in polymer concentration,²⁸ due to the influence of higher organic phase viscosity on the shearing efficiency of the stirrer.²⁸

Nanoparticles manufacturing process analysis

Z-ave is a crucial attribute governing acceptance or rejection of a particular nanoparticle batch. It is therefore of upmost importance to control this attribute over the manufacturing process. In the present study, Z-ave was controlled at three different stages by Dynamic Light Scattering (DLS) (Zetasizer® Nano ZS, Malvern Instruments, UK). Accordingly, the Z-ave for a test batch (10% (w/v) PVA, 0.2 dl g⁻¹ PolVisc, 2.5% (w/w) OVA) was 190.7 nm after sonication, 176.7 nm after addition of the w/o/w emulsion dropwise to 0.25% (w/w) poly(vinyl alcohol) external phase; finally, the suspension of solid PLGA showed a Z-ave of 188.2 nm at the end of the manufacturing process, after the centrifugation and washing steps. Therefore, the Z-ave of the final product of nanoparticles with this specific composition (10% PVA, 0.2 dl g⁻¹ PolVisc, 2.5% (w/w) OVA) was similar to the Z-ave obtained for the emulsion droplets in process. As a result, during the development process of PLGA nanoparticles by the double emulsion solvent evaporation techniques, the Z-ave can be accurately controlled through the determination of the size of the droplets of this emulsion. This will allow a real-time control of the size of the formulation, overcoming the need for an additional period of 3 hours to ensure solvent evaporation and particle recovery towards the control of the final product.

The importance of adequately tune the manufacturing process of PLGA nanoparticles to achieve robustness and particles with desired properties was addressed by Draheim et al. (2015).¹³ In this study, a fractional factorial design was employed to plan experiments towards the optimisation of two distinct manufacturing processes (nanoprecipitation and spray-drying) used for the formulation of nanoparticles with the required mean particle size, size distribution and yield. The authors reported that the polymer concentration was the most important factor to control batch-to-batch variability of nanoparticles prepared by the nanoprecipitation process. The developed mathematical models based on 34 experiments, including repetition of 5 experiments, allowed for the prediction of both size and size distribution of these nanocarriers. These studies evidenced that higher polymer concentrations led to larger particles. On the other hand, the experiments evidenced that the spray-drying method was influenced by multiple factors, being considerable difficult to control.

Our manufacturing process led to a narrow particle size distribution, with a PdI always lower than 0.200, ranging from 0.043 to 0.213. The PolVisc (single and quadratic terms) was the only statistically significant factor retained by the model optimization process. The relation between PdI and the PolVisc is therefore quadratic, with a minimum value of particle size distribution width (0.08) obtained for a PolVisc of 0.6 dl g⁻¹ (Fig. 2). PolVisc lower and higher than 0.6 dg l⁻¹ increased the PdI.

Fig. 2 Main effect plot showing the influence of PolVisc on the PdI.

The nanoparticles shape, size and surface morphology were analysed by Atomic Force Microscopy (AFM). The nanoparticles had a spherical shape (Fig. 3A), homogenous size distribution and hydrodynamic diameter lower to the one obtained by DLS (Fig. 3C) (AFM: 165.6 ± 45.1 nm, DLS: 195.1 ± 3.9 nm), and evidencing surface roughness (Fig. 3B). Silva et al. (2014) obtained a similar trend in nanoparticles size.²⁹ However, surface roughness herein evidenced by these optimized PLGA-based nanoparticles may be due to the absence of PEG chains, in contrast to the smooth surface presented by OVA-loaded PEGylated PLGA/poly-ε-caprolactone nanoparticles described in Silva et al. (2014) previous work.²⁹

Fig. 3 Nanoparticles surface morphology by AFM (715 × 715 nm²). Topography (A), phase (B) and nanoparticles diameter (C). Mean diameters were calculated from 50 individual nanoparticles from section analysis of three different areas.

The ZP of the PLGA nanoparticles was close to neutrality in all experiments, ranging from −4.24 to −1.07 mV. Modeling these data yielded a model structure involving two factors: PolVisc (single and quadratic terms) and OVA (single term). The model for ZP indicates that the highest value for surface charge (−2.4 mV) occurred when PolVisc was between 0.6 and 0.8 dl g⁻¹, coupled with a low OVA (Fig. 1B). PolVisc lower and higher than this range, combined with higher OVA, generated a decrease in the nanoparticles' ZP.

According to ZP response, Yerlikaya et al. (2013) considered the surfactant concentration an important factor (p-value = 0.208, Plackett–Burman).²⁶ In our study, the factor PVA was not statistically significant (p-value = 0.88). On the other hand, OVA was considered the factor (p-value = 0.05) that had the highest impact on the ZP of PLGA nanoparticles. This may be due to the adsorption of ovalbumin onto the surface of the nanoparticles, due to its negative charge at solvent pH. This fact is supported by Verma et al. (2009) that showed a more negative ZP for indomethacin particles in the presence of Dowfax 2A1, a negatively charged stabilizer, due to its adsorption onto nanoparticle surface.³⁰

Experimental values for EE ranged from 12.96% to 88.38%. Modeling this attribute revealed that within the experimental conditions adopted, the EE was governed by both PVA and OVA (single and interaction terms). Within the tested factors' range, higher PVA in the internal phase plus higher OVA led to lower EE (Fig. 4). Regarding EE response, Yerlikaya et al. (2013) also considered the surfactant concentration in the aqueous phase as an important factor that influences this QCA (our p-value = 0.0070; p-value = 0.205, Blackett–Burman).²⁶ In our study, an increase in the PVA decreased the EE. This was also observed by Rahman et al. (2010) and may be attributed to the higher ovalbumin partitioning into the external phase.^27,28

Fig. 4 Contour plot showing the influence of OVA and PVA on the EE (simulation considering PolVisc = 0.6 dl g⁻¹).

Experimental data for LC ranged from 3.24 to 24.98 μg mg⁻¹ for formulations prepared following the DoE conditions. All factors are included in the model and appear to have an antagonistic effect on LC (Fig. 5). In addition to the single terms, an interaction term between the PolVisc and OVA was found to be significant. If a value of 2.5% (w/w) is considered for OVA, the influence of PolVisc and PVA on LC was easily identified, as shown in Fig. 5. The LC decreases when the PolVisc increases. An inverse pattern was observed for PVA, where lower values led to higher LC.

Fig. 5 Contour plot showing the influence of PVA and PolVisc on the LC (simulation considering OVA = 2.5%).

Different proteins and peptides have been explored as antigens associated to PLGA nanoparticles as potential vaccine candidates. Besides ovalbumin, bovine serum albumin (BSA) and ovalbumin class I and class II epitopes are among the most explored ones.^31–34 The molecular weight and isoelectric point of proteins can indeed influence the nanoparticle physicochemical properties, namely the LC and Z-ave. However, multiple reports indicate that the double emulsion solvent evaporation technique used in the formulation of these nanoparticulate vaccines is a versatile but robust methodology, allowing for the successful development of nanoparticulate carriers presenting similar mean diameters and LC for proteins of different physical and chemical properties, such as ovalbumin and BSA, but also small peptides.³⁵ We have previously demonstrated that the Z-ave, PdI, ZP and LC of PLGA-based nanoparticles was not affected by the molecular weight of entrapped antigens, namely ovalbumin or the peptides Melan-A: 26–35(L27), gp100: 209–217(2M) or gp100: 44–59.³⁶ Therefore, one can expect similar factors to be considered when defining the experimental design.

The FTIR analysis allows the assessment of the chemical composition of ovalbumin-associated PLGA nanoparticles, providing data regarding the nature of protein-polymer interactions and thus the compatibility between the protein and polymeric components of these carriers. The FTIR spectra profiles obtained for both PLGA nanoparticle and ovalbumin-loaded PLGA nanoparticle are similar to the one obtained for the PLGA polymer (Fig. 6). It is evident a strong stretching absorption at 1770–1740 cm⁻¹, which indicates the presence of the carboxylic group (C=O bond). In addition, there are no visible changes in the position of the typical peaks of the ovalbumin in the FTIR of spectrum ovalbumin-loaded PLGA nanoparticles and no shift can also be identified for the O–H stretching (3500–3200 cm⁻¹) of the PLGA polymer.^37–39 In fact, the specific bands of the functional groups of the polymer in the nanoparticle are not different from those visible in the pure material. Therefore, the molecular interactions that could be established between the polymer and the protein and alter the chemical structure of the protein did not occur. As a result, it can be expected an adequate protection of the entrapped ovalbumin by the polymeric matrix.

Fig. 6 FTIR spectra of PLGA nanoparticles and formulation components. Band at 1770–1740 cm⁻¹ is specific for the carboxylic group (C=O bond), while 3500–3200 cm⁻¹ corresponds to the O–H groups.

Models' validation

To validate models, an additional experiment was conducted. This experiment was defined as using factor levels able to generate a nanoparticle with optimal attributes, hereby designed by specifications. These specifications were defined according to target values of the five attributes recognized as suitable for the optimal delivery and capture of extensive amounts of antigens to antigen-presenting cells (APCs). The Z-ave should be between 190.0 and 220.0 nm, because this size range enables high EE and LC levels, but also promotes nanoparticle delivery through the lymphatic system.⁴⁰ Similarly, low PdI values (between 0.10 and 0.15) should be obtained, evidencing homogeneous and stable formulation samples with no aggregates. The ZP should be close to neutrality (between −4.0 and 4.0 mV) as neutral surface charged nanoparticles are less cytotoxic than charged ones, being also less captured and therefore metabolized by the non-specific first line of defence. The EE and LC levels should be the highest to enable the maximum content inside the nanoparticles. Specifications were then set to values of EE ranging from 90.0 to 99.0%, and 24.0 to 25.0 μg mg⁻¹ for LC. The set of factors able to generate a nanoparticle with these characteristics was estimated by running the optimizer feature in MODDE. Target values comprising a range of minimum and maximum values (tolerance for the optimizer) were set. The optimizer predicted a formulation with the following factors: PVA = 11% (w/v), PolVisc = 0.6 dg l⁻¹ and OVA = 2.5% (w/w). This experiment was conducted and experimental values for the five responses were compared to models' predictions (Table 3).

Table 3 Target formulation specifications and models' validation for a nanoparticle prepared with PVA = 11%, PolVisc = 0.6 dl g⁻¹ and OVA = 2.5%

Specification	Minimum allowed	Target	Maximum allowed	Experimental	Model prediction
a Experimentally determined value within the model's predicted interval.
Z-ave (nm)	—	190.0	220.0	189.3 ± 0.778	191.7 ± 6.95^a
PdI	—	0.10	0.15	0.044 ± 0.027	0.079 ± 0.026
ZP (mV)	−4.0	0.0	4.0	−2.28 ± 0.424	−2.66 ± 0.4^a
EE (%)	—	90.0	99.0	45.62 ± 0.622	59.76 ± 10.57
LC (μg mg^−1)	—	24.0	25.0	11.40 ± 0.156	14.87 ± 3.925^a

---

The experimental values for these nanoparticles were globally well predicted by the five models. Moreover, the average value for each attribute was within the model's 95% prediction limits, except for PdI and EE, where the experimental values were outside, but considerably close to predicted lower limits. These results clearly confirm the prediction ability of the developed models, and corroborate the higher prediction accuracy of the models presenting higher range error ratio (RER) and lower root mean square error (RMSE) statistics. These results might indicate that within the tested factors' range, probably some relationships are more complex, thus not being well predicted by these relatively simple linear models with interaction and quadratic terms. A non-linear modelling strategy could unveil this hypothesis, although at an expense of a greater number of experiments and a tighter models' validation.⁴¹ On the other hand, one should not exclude the possibility that other non-voluntary uncontrolled factors can affect the experiments outcome. Therefore, a combination of these two possibilities should be explored in the future towards a more robust identification of the factors-responses relationship allowing more accurate models and thus with more applicability in practice.

Design space

A design-space was estimated from the three factors (PolVisc, PVA and OVA). The developed models for the five attributes supported the proposing design-space (Fig. 7). To estimate the design-space boundary, a risk of failure limit of 1000 DPMO was considered. Accordingly, the acceptable region that fulfill those targeted features is achieved when 2.5% (w/w) OVA are entrapped within nanoparticles. The manufacturing process should use a PolVisc ranging from 0.4 to 0.9 dl g⁻¹ and a PVA between 8 and 15% (w/v) to ensure that the attributes remain within the specifications.

Fig. 7 Design-space for a formulation with properties as shown in Table 3, represented in terms of the variation of PolVisc and PVA, while considering a constant value for OVA (2.5%). The design-space was built considering a risk of failure (DPMO) limit of 1000.

Interaction of optimized nanoparticles with targeted cells

Dendritic cell viability in the presence of nanoparticles. In order to evaluate the effect of PLGA nanoparticles on the viability of JAW SII murine immature dendritic cells, an Alamar Blue® assay was performed (Fig. 8). The assay did not evidence a negative impact of PLGA nanoparticles on the viability of the tested cells. The cell viability was close to 100% for all the concentrations of nanoparticles, after 24 h of incubation (data not presented). Moreover, no significant differences were observed even after 48 h of incubation with 1000 μg mL⁻¹ of nanoparticles. A similar profile was achieved by Silva et al. (2014) where cell viabilities were higher than 70% after 48 h of incubation of PLGA nanoparticles with JAWSII cells.²⁹ These results show that the manufacturing process led to nanoparticles which residual amounts of organic solvent and surfactant do not affect the viability of targeted cells. In fact, the lack of biocompatibility has been previously reported for PVA,⁴² and the use of organic solvents is pointed as one of the major disadvantages concerning the preparation of vaccine carriers by emulsion evaporation methods.⁴³ Our data is in line with our previous study in which poly-ε-caprolactone-based vaccine carriers prepared by the solvent emulsion evaporation method presented a residual value for dichloromethane (DCM) lower than the one accepted by regulation authorities, and did not affect the viability of BALB/c mouse monocyte macrophage J774A.1 cell line.⁴³

Fig. 8 Cell viability of JAWSII murine immature dendritic cells in the presence of PLGA nanoparticles. Mean ± SD; N = 3, n = 6, where N stands for number of independent experiments and n stands for number of measurements per experiment. One-way ANOVA and Tukey's Post Hoc test were used to compare cell viability in the four different nanoparticle concentrations; *p < 0.001 (related to Triton X-100).

Uptake study of nanoparticles. In order to analyse if the nanoplatforms could be internalized by JAWSII murine immature dendritic cells, flow cytometry studies were carried out. The nanoparticles were extensively internalized by the phagocytic cells (Fig. 9). The use of Rhodamine-grafted PLGA polymer to obtain fluorescently-labelled nanoparticles instead of Rhodamine-entrapped nanoparticles is important in order to avoid wrong interpretations as a result of Rhodamine leakage.²⁹

Fig. 9 Internalization profile of nanoparticles by JAW SII cells after 3 h, 24 h and 48 h of incubation, expressed by percentage of positive cells in the sorted population by flow cytometry. Mean ± SD; N = 2, n = 3, where N stands for the number of independent experiments and n stands for the number of measurements per experiment. One-way ANOVA and Tukey's Post Hoc test were used to compare uptake at any time point to 3 h incubation: *p < 0.01 and **p < 0.001.

The internalization levels increased with the incubation time (at 3 h: 6.6 ± 2.4 Rhodamine + cells (%) at 3 h; 60.1 ± 4.7% at 24 h and 79.9 ± 1.9% at 48 h). Similar uptake profiles were recently reported by Silva et al. (2014) and Kulkarni et al. (2013).^29,44 According to Kulkarni et al. (2013) the cellular uptake was higher for nanoparticles in a size range of 100–200 nm.⁴⁴ The optimized nanoparticles used in this uptake study are within this size range. Silva et al. (2014) compared the uptake profile of PLGA nanoparticles by immature bone marrow-derived dendritic cells (BMDCs) and the cell line JAWSII²⁹ by flow cytometry and data was confirmed by confocal microscopy. It was possible to observe that nanoparticles were taken up by the JAWSII cell line at lower extent than the primary dendritic cells, but the amount of nanoparticles in the interior of targeted cells increased with time of incubation and nanoparticle concentration.²⁹ On the other hand, the uptake profile by BMDCs was totally different, being close to 60% from 3 h to 24 h, thus not dependent on time or even concentration.

In addition of an extensive uptake of antigen-loaded PLGA nanoparticles by dendritic cells, the activation and effective maturation of these APCs will only occur upon a sustained release of the antigen from the carrier. One of the major advantages widely recognized among the scientific community to PLGA-based polymers is the possibility for adjusting their physical and chemical properties in order to obtain a degradation and release profiles suited for the targeted biological effect. Properties such as crystallinity, glass transition temperature, solubility and molecular weight can have a pronounced effect on polymer physicochemical properties, and thus dictate payload release kinetics. PLGA mechanical properties and degradation rates can be adjusted according to the ratio and molecular weight of both monomers lactic and glycolic acids. The antigen release kinetics can have an important impact in the immune response.^29,45 PLGA degradation in buffer or biological fluids occurs through the hydrolytic cleavage of ester bonds, yielding to the accumulation of both lactic and glycolic acids. Even if the mechanisms of release are not completely understood, it is reported that it is initially driven by diffusion, while degradation/erosion is accepted to be the major factor at the end of the release process.^46,47 The latter is highly dictated by the PLGA molecular weight and end-group caps.^48,49 It was also demonstrated that diffusion has a major impact in the release rate from low molecular weight PLGA polymers, while both diffusion and erosion should be considered when evaluating the degradation profiles of those polyester polymers presenting high molecular weights.^50,51

Tri-phasic release profile were reported to PLGA-based nano and microparticles, evidencing an initial burst effect, followed by a lag-phase mostly due to the diffusion-release mechanism, and finally an accelerate release due to the erosion of the matrix.^48,50 It is accepted that the initial burst release may be due to the release of protein adsorbed onto nanoparticle surface.

The release study did not show an initial burst release of the ovalbumin, and evidenced that approximately 5% (w/w) and 13% (w/w) of the antigen initially entrapped in the PLGA nanoparticles was detected after 1 and 3 weeks of incubation. These data are in line with the expected degradation time for the PLGA polymer used for the formulation of nanoparticles, which can range from 4–5 months.^46,52 As a result, we can expect a sustained release of the antigen from the nanoparticles developed, which is of particular importance for the development of a long lasting immune response.

Experimental

Materials

PLGA Resomer® RG 755 s, 752 s and 750 s (lactide : glycolide molar ratio 75 : 25, with inherent viscosities of 0.6, 0.2 and 1 dl g⁻¹, respectively) were purchased from Boehringer Ingelheim GmbH (Ingelheim, Germany). Poly(vinyl alcohol) (MW 13000–23000 Da), ovalbumin, dichloromethane (DCM), phosphate buffered saline tablets, magnesium chloride, calcium chloride, Granulocyte-Macrophage Colony-Stimulating Factor human (GM-CSF) and potassium bromide (KBr) were supplied by Sigma-Aldrich (St. Louis, MO, USA). RPMI 1640 Medium GlutaMAXTM Supplement, Fetal bovine serum (FBS), sodium pyruvate 100 mM, penicillin streptomycin, 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES) solution buffer 1 M, 2-mercaptoethanol 50 mM and AlamarBlue® were purchased from ThermoFisher Scientific (Waltham, Massachusetts, USA). JAWSII murine immature dendritic cells (ATCC® CRL-11904 TM) were obtained from American Type Culture Collection (ATCC, Manassas, VA, USA). Rhodamine 6G derivative (9-(2-((carboxymethoxy)carbonyl)phenyl)-3,6-bis(ethylamino)-2,7-dimethylxanthylium bromide) was synthesized and conjugated to PLGA as described elsewhere.⁵³

Preparation of PLGA nanoparticles

The PLGA (75/25, w/w) nanoparticles were prepared following a w/o/w double emulsion–solvent evaporation method previously developed, with specific modifications.³⁶ Briefly, the PLGA polymer was dissolved in DCM and this organic phase was further emulsified with a poly(vinyl alcohol) solution (aqueous phase) at different concentrations, using a sonicator (Branson S-250D, 50/60 Hz, 20 kHz) for 15 seconds at 20% amplitude. Fluorescent nanoparticles were formulated by replacing a tenth of the PLGA mass by Rhodamine-labelled PLGA. Different amounts of ovalbumin, the model antigen, were dissolved into the aqueous phase according to the designed experiment. The second emulsion was formed after addition of 1.25% (w/v) poly(vinyl alcohol) using the conditions mentioned above. The double emulsion was added dropwise to 0.25% (w/v) poly(vinyl alcohol) solution and stirred during 1 h at room temperature, allowing for solvent evaporation. The nanoparticles were retrieved from the suspension by centrifugation at 17 500 rpm, 4 °C for 45 min (Beckman Coulter Avanti J-E Centrifuge, JA-20 rotor). Nanoparticles were washed twice with purified water by centrifugation, under the same conditions. The pellet was resuspended in Dulbecco's phosphate buffered saline (DPBS), and stored at 4 °C until analysis.

Experimental design

A three level full factorial experimental design was performed resourcing to the software MODDE version 10.1 (MKS Umetrics, Sweden).^54,55 PolVisc (0.2 dl g⁻¹, 0.6 dl g⁻¹, 1 dl g⁻¹), PVA (5% (w/v), 10% (w/v), 15% (w/v)) and OVA (0% (w/w), 2.5% (w/w), 5% (w/w)) were the varied manufacturing conditions (factors). The PolVisc corresponds to the PLGA inherent viscosity measured at 25 °C, 0.1% (w/v) in chloroform, with a size 0c Ubbelohde glass capillary viscometer. The PVA corresponds to the amount of poly(vinyl alcohol) added in the internal aqueous phase. The OVA corresponds to ovalbumin percentage of the used polymer's mass. The hydrodynamic diameter (Z-ave), polydispersity index (PdI), zeta potential (ZP), entrapment efficiency (EE) and loading capacity (LC) were the evaluated properties (responses). Summing to the design 27 experiments, three replicates of the central point (to access model's lack-of-fit) were performed totalizing 30 experiments (Table 1). In addition to the DoE experiments, an additional test was produced using factor levels pointed-out by the developed mathematical models towards the production of a formulation with targeted specifications (see results and discussion section). The experiments were conducted in a random order as it is typically done to allow the greatest reliability and validity of statistical estimates. Experiment results were modelled by multiple linear regression and obtained models evaluated by analysis of variance (ANOVA).

Nanoparticles analysis

Physicochemical characterisation. Z-ave and PdI were determined by Dynamic Light Scattering (DLS) (Zetasizer® Nano ZS, Malvern Instruments, UK). ZP was measured by Laser Doppler Electrophoresis (Malvern Instruments, Worcestershire, UK). All measurements were performed in triplicate using nanoparticles dispersed in DPBS (20 mg mL⁻¹) at 25 °C.

Nanoparticles surface morphology evaluation. The nanoparticles (PVA = 11% (w/v), PolVisc = 0.6 dg l⁻¹ and OVA = 0% (w/w)) size, shape and surface morphology were evaluated by Atomic Force Microscopy (AFM), using a Nanoscope IIIa Multimode AFM (Digital Instruments, Veeco).²⁹ Nanoparticle were diluted to 10 mg mL⁻¹ with purified water. The samples were added dropwise to cleaved mica at room temperature and dried with N₂. The AFM analyses were performed at a scan rate of approximately 1.6 Hz, using tapping mode in air at room temperature with etched silicon tips (ca. 300 kHz), obtaining topography and phase images.

Entrapment efficiency and loading capacity assessment. The EE and LC were determined by the indirect method, analysing the amount of ovalbumin released in the supernatants by HPLC (eqn (1) and (2)).

In eqn (1), ovalbumin₀ is the initial amount of ovalbumin and ovalbumin_sup is the amount of ovalbumin in the supernatant. In eqn (2), polymer is the amount of polymer.

The determination of OVA was performed using a Beckman System Gold HPLC (Beckman Coulter Inc.), with a Shodex Protein KW-803 column (8.0 mm ID × 300 mm, 5 μm particle size, 300 Å pore size) at room temperature, injecting samples with a volume of 20 μl. The mobile phase was composed of sodium phosphate buffer 50 mM at pH 7.0 and sodium chloride 0.3 M. The eluent flow rate was 1.0 mL min⁻¹, for 15 min. The signal was monitored at 220 nm by spectrophotometric analysis (Hitachi U-2001 UV-vis Spectrophotometer, USA).

FTIR characterization of PLGA nanoparticles. PLGA nanoparticles were lyophilized (Modulyo freeze-dryer (Edwards, Germany)) in the presence of the cryoprotectant sucrose (0.05% w/w) for 18 h at an initial temperature of −40 °C and 0.1 mBar. Lyophilized nanoparticles and the controls were mixed with KBr at a concentration of 1.5% (w/w) and compressed into a tablet (12 mm diameter) using a manual tablet presser. The infrared spectra were measured at the transmittance mode with 30 scans and a resolution of 2.0 cm⁻¹ (Affinity-1 Shimadzu spectrophotometer, Japan).

Modelling

Multiple linear regression was used to model the five responses against the three factors,⁵⁶ resourcing to the software MODDE version 10.1 (MKS Umetrics, Sweden). To model EE and LC, plain nanoparticle experiments were discarded since the amount of protein in these samples is zero (eqn (1) and (2)). Before modelling, factors and responses were auto-scaled (average removal and division by the variance). Models' performance was assessed by calculating the root mean square error (RMSE) and range error ratio (RER) parameters.

In eqn (3), Y_i is the experimentally observed value for sample i, Ŷ_i is the model predicted value for sample i and n is the number of samples.

In eqn (4), Y_max is the maximum value of the response, Y_min is the minimum value of the response.

Models' validation and design-space

The optimised models were used to estimate the manufacturing properties ideal to attain the nanoparticle specifications required for optimal delivery of antigens to targeted phagocytic cells.²¹ Accordingly, these nanotechnology-based vaccines should present mean size diameter lower than 200 nm, monodisperse population (PdI ≤ 0.200) and neutral surface charge, in order to enhance their capture by dendritic cells, which are known as the most potent professional APCs.²¹ This was achieved using the optimiser feature of MODDE version 10.1 (MKS Umetrics, Sweden), which includes a simplex algorithm for optimisation. The targeted specifications aforementioned were introduced in the optimiser and series of estimations of the three factors were proposed. The estimation featuring the highest determinant was selected for the preparation of a batch of nanoparticles, in triplicate. The physicochemical properties of these carriers were determined, as described in Section 2.4. The developed models were validated through the comparison between predictions and experimental values. The estimated design-space was constructed around the nanoparticulate system presenting the targeted specifications, applying the developed models for the five responses with MODDE version 10.1 (MKS Umetrics, Sweden). The design-space was built in terms of default per million opportunities (DPMO).

Interaction of nanoparticles with targeted cells

Conditions of cell culture. JAWSII murine immature dendritic cells were propagated in RPMI medium with GlutaMAX with 10% (v/v) FBS, 1% (v/v) sodium pyruvate, 1% (v/v) penicillin streptomycin, 1% (v/v) HEPES buffer, 0.1% (v/v) 2-mercaptoethanol and 0.005% (v/v) GM-CSF.

In vitro cell viability. Cell viability of JAWSII murine immature dendritic cells in the presence of PLGA nanoparticles (PVA = 11% (w/v), PolVisc = 0.6 dg l⁻¹ and OVA = 2.5% (w/w)) was inferred by using AlamarBlue® Assay. The cells (1 × 10⁴) were incubated overnight at 37 °C and 5% CO₂ and treated with increasing concentrations of nanoparticles (125, 250, 500 and 1000 μg mL⁻¹) for 48 h. AlamarBlue® was added in an amount of 10% (v/v) of the well volume and the plates were read after 3 hours of incubation (37 °C and 5% CO₂) with the reagent. The absorbance was measured at two different wavelengths: 570 and 630 nm using a microplate reader (Biotek, ELx800, USA). The controls used in the assay were PBS (negative control) and Triton X-100 0.5% (v/v) (positive control).

In vitro uptake study by flow cytometry. JAWSII cells (65 000/195 μl per well) were seeded in 96-well flat bottom plates and incubated overnight at 37 °C and 5% CO₂. The uptake of the Rhodamine-PLGA nanoparticles at 0.5 mg mL⁻¹ (PVA = 11% (w/v), PolVisc = 0.6 dg l⁻¹ and OVA = 0% (w/w)) by JAWSII murine immature dendritic cells was evaluated at three different time points: 3 h, 24 h and 48 h. Nanoparticles were added to the cells (0.5 mg mL⁻¹) and incubated at the conditions mentioned above, for the indicated periods. Cells were then washed twice with PBS, harvested by centrifugation (1000 rpm, 5 min, 4 °C) and resuspended with flow cytometry buffer (PBS sterile buffer + 2% (v/v) FBS). The fluorescence was analyzed at 530 nm with excitation at 488 nm using an LSRFortessa2 cytometer (BD Biosciences) with High Throughput Sampler (HTS). Untreated cells were used as control and the results were analyzed with FlowJo software version 9.8 for Microsoft (TreeStar, San Carlos, CA).

Conclusions

This study evaluated the effect of PVA, PolVisc and OVA (the factors) on five critical PLGA nanoparticles' attributes ZP, PdI, Z-ave, LC and EE (the responses) during the double emulsion solvent evaporation process. Experiments carried out according to the proposed experimental design allowed the identification of the major factors related with the responses. This identification was based on the development of linear models and assessment of statistical significance. All factors were found to be relevant to explain the variability observed on both Z-ave and LC. PdI variability was mainly influenced by the PolVisc. PVA and OVA were the major sources of variability in EE and PolVisc, while OVA influenced the ZP response. One of the major aims in PLGA nanoparticles' production is to achieve desired values for the nanoparticles' properties, while ensuring the lowest possible batch-to-batch variability. This paper demonstrates that a QbD approach is applicable to estimate a design-space allowing the developer to understand relationships between CPPs and CQAs, thus being able to adjust critical variables according to the desired nanoparticles' specifications. In the particular system explored in this work, the developed mathematical models were able to estimate actual nanoparticles' properties with accuracy adequate for practical use. The mathematical models were employed to estimate the manufacturing conditions needed to achieve a formulation with optimal characteristics (PVA 11%, polymer 0.6 dl g⁻¹ and OVA 2.5%). These conditions were then tested experimentally and the properties of the resulting nanoparticles were found to be in accordance with mathematical models prediction (within the confidence limits). Future studies will investigate the advantages of modelling this system with non-linear methods in order to further increase the models' accuracy. Additionally, other possible sources of process variability will be explored to be included in the models.

Author contributions

V. S., C. P. and T. Ciman performed the majority of the experimental work. C. R. and C. A. M. A. developed the synthesis of the Rhodamine-grafted PLGA polymers. A. S. V. performed the AFM analysis and analysed and discussed related data. V. S. wrote the paper and conducted the main literature search; M. Z. and T. B. structured and supervised the manuscript. All authors conducted literature search and contributed to the sections on their specialty, H. F. and R. S. G. nanoparticle formulation and interaction with targeted cells, S. B. characterization and applications of polymeric-based carriers, chemistry, M. Z. modeling and J. L. QbD and PAT. All authors read and approved the final manuscript.

Acknowledgements

The authors thank to Fundação para a Ciência e a Tecnologia, Ministério da Ciência e da Tecnologia, Portugal for PhD Grants SFRH/BD/87869/2012 to Vanessa Sainz, and SFRH/BD/87591/2012 to Carina Peres); research projects (UTAP-ICDT/DTP-FTO/0016/2014 and ENMed/0003/2015) and iMed.ULisboa grant UID/DTP/04138/2013. This work was also partially funded by Gilead Sciences Program (PGG/037/2014).

Notes and references

1. V. Sainz, J. Conniot, A. I. Matos, C. Peres, E. Zupancic, L. Moura, L. C. Silva, H. F. Florindo and R. S. Gaspar, Biochem. Biophys. Res. Commun., 2015, 468, 504–510.
2. K. M. Tyner, P. Zou, X. Yang, H. Zhang, C. N. Cruz and S. L. Lee, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2015, 7, 640–654.
3. C. W. Noorlander, M. W. Kooi, A. G. Oomen, M. V. Park, R. J. Vandebriel and R. E. Geertsma, Nanomedicine, 2015, 1–10.
4. C. A. Schütz, L. Juillerat-Jeanneret, H. Mueller, I. Lynch and M. Riediker, Nanomedicine, 2013, 8, 449–467.
5. R. Paliwal, R. J. Babu and S. Palakurthi, AAPS PharmSciTech, 2014, 15, 1527–1534.
6. S. Tinkle, S. E. McNeil, S. Mühlebach, R. Bawa, G. Borchard, Y. C. Barenholz, L. Tamarkin and N. Desai, Ann. N. Y. Acad. Sci., 2014, 1313, 35–56.
7. S. Mühlebach, G. Borchard and S. Yildiz, Nanomedicine, 2015, 10, 659–674.
8. L. X. Yu, Pharm. Res., 2008, 25, 781–791.
9. F. Lagarce, Eur. J. Nanomed., 2015, 7, 77–78.
10. ICH, Q8(R2) Pharmaceutical Development, 2009, Available from:https://www.pmda.go.jp/files/000156835.pdf, Last accessed January 2016.
11. J. N. Sangshetti, M. Deshpande, Z. Zaheer, D. B. Shinde and R. Arote, Arabian J. Chem., 2014 DOI:10.1016/j.arabjc.2014.01.025.
12. J. K. Drennen III, Journal of Pharmaceutical Innovation, 2007, 2, 65–66.
13. C. Draheim, F. de Crécy, S. Hansen, E.-M. Collnot and C.-M. Lehr, Pharm. Res., 2015, 1–16.
14. D. Kumar, B. J. Meenan, I. Mutreja, R. D'SA and D. Dixon, Int. J. Nanosci., 2012, 11, 1250023.
15. N. E.-A. El-Naggar and N. A. Abdelwahed, J. Microbiol., 2014, 52, 53–63.
16. J. Zhang, Y. Fan and E. Smith, J. Pharm. Sci., 2009, 98, 1813–1819.
17. B. Shah, D. Khunt, H. Bhatt, M. Misra and H. Padh, Eur. J. Pharm. Sci., 2015, 78, 54–66.
18. B. K. Patel, R. H. Parikh and P. S. Aboti, J. Drug Delivery, 2013, 2013, 370938.
19. A. F. Ribeiro, C. T. G. Ferreira, J. F. dos Santos, L. M. Cabral and V. P. de Sousa, J. Nanopart. Res., 2015, 17, 1–16.
20. F. Danhier, E. Ansorena, J. M. Silva, R. Coco, A. Le Breton and V. Préat, Journal of controlled release, 2012, 161, 505–522.
21. J. M. Silva, M. Videira, R. Gaspar, V. Préat and H. F. Florindo, J. Controlled Release, 2013, 168, 179–199.
22. A. Giteau, M.-C. Venier-Julienne, S. Marchal, J.-L. Courthaudon, M. Sergent, C. Montero-Menei, J.-M. Verdier and J.-P. Benoit, Eur. J. Pharm. Biopharm., 2008, 70, 127–136.
23. M. Garinot, V. Fiévez, V. Pourcelle, F. Stoffelbach, A. des Rieux, L. Plapied, I. Theate, H. Freichels, C. Jérôme and J. Marchand-Brynaert, J. Controlled Release, 2007, 120, 195–204.
24. L. Choisnard, A. Géze, M. Bigan, J.-L. Putaux and D. Wouessidjewe, J. Pharm. Pharm. Sci., 2005, 8, 593–600.
25. T. Naes, T. Isaksson, T. Fearn and T. Davies, A user friendly guide to multivariate calibration and classification, NIR publications, 2002.
26. F. Yerlikaya, A. Ozgen, I. Vural, O. Guven, E. Karaagaoglu, M. A. Khan and Y. Capan, J. Pharm. Sci., 2013, 102, 3748–3761.
27. Q. Yang and G. Owusu-Ababio, Drug Dev. Ind. Pharm., 2000, 26, 61–70.
28. Z. Rahman, A. S. Zidan, M. J. Habib and M. A. Khan, Int. J. Pharm., 2010, 389, 186–194.
29. J. M. Silva, G. Vandermeulen, V. G. Oliveira, S. N. Pinto, C. Rodrigues, A. Salgado, C. A. Afonso, A. S. Viana, C. Jérôme and L. C. Silva, Nanomedicine, 2014, 9, 2639–2656.
30. S. Verma, Y. Lan, R. Gokhale and D. J. Burgess, Int. J. Pharm., 2009, 377, 185–198.
31. Y.-R. Lee, Y.-H. Lee, K.-H. Kim, S.-A. Im and C.-K. Lee, Immune Network, 2013, 13, 30–33.
32. T. Gerelchuluun, Y.-H. Lee, Y.-R. Lee, S.-A. Im, S. Song, J. S. Park, K. Han, K. Kim and C.-K. Lee, Arch. Pharmacal Res., 2007, 30, 1440–1446.
33. D. Chitkara and N. Kumar, Pharm. Res., 2013, 30, 2396–2409.
34. G. Zhu, S. R. Mallery and S. P. Schwendeman, Nat. Biotechnol., 2000, 18, 52–57.
35. Y.-P. Li, Y.-Y. Pei, X.-Y. Zhang, Z.-H. Gu, Z.-H. Zhou, W.-F. Yuan, J.-J. Zhou, J.-H. Zhu and X.-J. Gao, J. Controlled Release, 2001, 71, 203–211.
36. J. M. Silva, E. Zupancic, G. Vandermeulen, V. G. Oliveira, A. Salgado, M. Videira, M. Gaspar, L. Graca, V. Préat and H. F. Florindo, J. Controlled Release, 2015, 198, 91–103.
37. N. Pirooznia, S. Hasannia, A. S. Lotfi and M. Ghanei, J. Nanobiotechnol., 2012, 10, 1.
38. S.-B. Sun, P. Liu, F.-M. Shao and Q.-L. Miao, Int. J. Clin. Exp. Med., 2015, 8, 19670.
39. A. Rudra, K. Santra and B. Mukherjee, Trends Appl. Sci. Res., 2011, 6, 47–56.
40. V. Manolova, A. Flace, M. Bauer, K. Schwarz, P. Saudan and M. F. Bachmann, Eur. J. Immunol., 2008, 38, 1404–1413.
41. J. A. Suykens, J. P. Vandewalle and B. L. de Moor, Artificial neural networks for modelling and control of non-linear systems, Springer Science & Business Media, 2012.
42. D. Chognot, J. Six, M. Leonard, F. Bonneaux, C. Vigneron and E. Dellacherie, J. Colloid Interface Sci., 2003, 268, 441–447.
43. H. Florindo, S. Pandit, L. Goncalves, H. Alpar and A. Almeida, Vaccine, 2008, 26, 4168–4177.
44. S. A. Kulkarni and S.-S. Feng, Pharm. Res., 2013, 30, 2512–2522.
45. S. L. Demento, W. Cui, J. M. Criscione, E. Stern, J. Tulipan, S. M. Kaech and T. M. Fahmy, Biomaterials, 2012, 33, 4957–4964.
46. N. Kamaly, B. Yameen, J. Wu and O. C. Farokhzad, Chem. Rev., 2016, 116, 2602–2663.
47. S. Fredenberg, M. Wahlgren, M. Reslow and A. Axelsson, Int. J. Pharm., 2011, 415, 34–52.
48. B. S. Zolnik and D. J. Burgess, J. Controlled Release, 2007, 122, 338–344.
49. A. Kumari, S. K. Yadav and S. C. Yadav, Colloids Surf., B, 2010, 75, 1–18.
50. K. Makino, T. Mogi, N. Ohtake, M. Yoshida, S. Ando, T. Nakajima and H. Ohshima, Colloids Surf., B, 2000, 19, 173–179.
51. M. Tracy, K. Ward, L. Firouzabadian, Y. Wang, N. Dong, R. Qian and Y. Zhang, Biomaterials, 1999, 20, 1057–1062.
52. J. C. Middleton and A. Tipton, Medical Plastic and Biomaterials, 1998, 5, 30–39.
53. C. A. Afonso, V. Santhakumar, A. Lough and R. A. Batey, Synthesis, 2003, 2647–2654.
54. G. A. Lewis, D. Mathieu and R. Phan-Tan-Luu, Pharmaceutical experimental design, CRC Press, 1998.
55. K. H. Esbensen, D. Guyot, F. Westad and L. P. Houmoller, Multivariate data analysis-in practice: an introduction to multivariate data analysis and experimental design, Multivariate Data Analysis, 2002.
56. D. C. Montgomery, E. A. Peck and G. G. Vining, Introduction to linear regression analysis, John Wiley & Sons, 2012.

---