Lattice dynamics of a quasi-2D layered TlCo2Se2 with a helical magnetic structure
Grzegorz Jagło and
Urszula D. Wdowik *
*
Institute of Technology, Pedagogical University, ul. Podchorazych 2, 30-084 Cracow, Poland. E-mail: sfwdowik@cyf-kr.edu.pl
First published on 10th August 2016
Abstract
The vibrational properties of a quasi-two-dimensional layered TlCo2Se2 compound exhibiting a helical magnetic order were investigated using density functional theory and an approximation of the harmonic phonons. The helical magnetic structure of this ternary dichalcogenide was shown to be stabilized by phonons. The dynamical properties of the TlCo2Se2 lattice conform with the quasi-2D layered structure of this compound. The intensities of the Raman and infrared active phonon modes of TlCo2Se2 remained sensitive to magnetic interactions, suggesting a rather strong spin–phonon coupling within the Co–Se layers. A detailed analysis of the calculated phonon, Raman and infrared absorption spectra of TlCo2Se2 which was carried out with respect to the spectra of its ferromagnetic (KCo2Se2) and paramagnetic (KNi2Se2) counterparts enabled the essential differences between the dynamical properties of the quasi-2D layered transition-metal dichalcogenides to be elucidated.
1 Introduction
The ternary layered compounds from the AT2X2 family (A = K, Rb, Cs, Tl; T = Fe, Co, Ni; X = S, Se, Te) have unique properties such as the superconductivity of Fe-based compounds1,2 and the charge-density waves and heavy-fermion behavior of Ni-based ones.3–5 These materials often exhibit interesting magnetic properties, which are attributed to their quasi-two-dimensional (quasi-2D) layered structure, which is shown in Fig. 1(a). The layers are built of edge-sharing TX4 tetrahedra extending two-dimensionally in the tetragonal plane, while the A ions which are coordinated by eight X ions are located between the layers.In general, localized magnetism is absent in ANi2X2 compounds, whereas in AFe2X2 materials an interplay between the superconducting (SC) metallic state and the non-superconducting, insulating antiferromagnetic (AF) state is observed.2 On the other hand, Co-based ternary dichalcogenides are metallic conductors showing mostly a ferromagnetic (FM) order.6–10 There are, however, two compounds within the ACo2X2 system which order antiferromagnetically, namely CsCo2Se2 (ref. 11–13) and TlCo2Se2.14–18 The latter remains unique among the Co-based ternary dichalcogenides as it exhibits an incommensurate helical magnetic structure14,15 below TN = 80–90 K, in which the Co spins order ferromagnetically within each layer containing Co ions (basal tetragonal plane) and the magnetic moments of the adjacent Co layers are rotated by about 121° with respect to each other. This leads to an incommensurate helix structure extending along the crystallographic c-axis, as is schematically shown in Fig. 1(b).
So far, TlCo2Se2 has been the subject of few theoretical studies which have focussed mainly on its electronic and magnetic structures.15,16,18 This work, based on state-of-the-art density functional theory (DFT), has provided insight at the atomic level into the phonon dynamics of the ternary dichalcogenide TlCo2Se2, and supplements the existing experimental and theoretical information on the fundamental properties of this quasi-2D layered material which exhibits an unusual magnetic order. The results of this research may serve as a guide for future neutron inelastic scattering, Raman and infrared experiments.
2 Methodology
Calculations were carried out within the spin-polarized density functional theory (DFT) implemented in the VASP code.19,20 Electron–ion interaction was represented by the projector augmented wave (PAW) method. The generalized gradient approximation with parametrization of Pedrew, Burke and Ernzerhof (GGA-PBE)21,22 was applied for the exchange and correlation potential. Plane waves up to an energy cutoff of 351 eV were used as basis functions. Reference configurations for valence electrons were (6s2 6p1) for Tl, (3d8 4s1) for Co, and (4s2 4p4) for Se. The incommensurate helical magnetic structure was approximated within the 1 × 1 × 3 supercell which consisted of 30 atoms and Θ = 120°, as indicated by previous experimental studies,14 and suggested an approximate repeat distance of 40 Å (3c). Lattice constants and internal atomic positions of this supercell were fully optimized with convergence criteria for the residual Hellmann–Feynman (HF) forces and the system’s total energy of 10−5 eV Å−1 and 10−7 eV, respectively. The k-point mesh of 12 × 12 × 12, generated according to the scheme of Monkhorst–Pack, was used for the Brillouin zone integration. Phonon calculations were performed within the direct method approach23,24 and harmonic approximation. The HF forces were obtained by displacing the symmetry non-equivalent Tl, Co and Se atoms from their equilibrium positions by ±0.02 Å in the 2 × 2 × 3 supercell containing 120 atoms. The HF forces were calculated with a reduced k-point mesh of 6 × 6 × 2. The total number of calculated displacements amounted to 12. The peak intensities of the non-resonant Raman spectrum (in Stokes process) were calculated from the well-known expression:25 I ∝![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |esRei|2ω−1(n + 1), where (n + 1) is the population factor for Stokes scattering with n = [exp(ℏω/kBT) − 1]−1 denoting the Bose–Einstein thermal factor, ei (es) is the polarization of the incident (scattered) radiation, R is the Raman susceptibility tensor. The components of R tensor (αij) were determined from derivatives of the electric polarizability tensor over the atomic displacements.24,26,27 The electric polarizabilities were calculated28 for each symmetry non-equivalent atom displaced from its equilibrium position by ±0.01 Å. The intensities of the peaks in the infrared (IR) absorption spectra were computed according to the formalism described in ref. 24, 29 and 30. The intensities of the infrared absorption spectrum of the transverse optical phonons having frequencies ωT at the Brillouin zone center take on the form:
|esRei|2ω−1(n + 1), where (n + 1) is the population factor for Stokes scattering with n = [exp(ℏω/kBT) − 1]−1 denoting the Bose–Einstein thermal factor, ei (es) is the polarization of the incident (scattered) radiation, R is the Raman susceptibility tensor. The components of R tensor (αij) were determined from derivatives of the electric polarizability tensor over the atomic displacements.24,26,27 The electric polarizabilities were calculated28 for each symmetry non-equivalent atom displaced from its equilibrium position by ±0.01 Å. The intensities of the peaks in the infrared (IR) absorption spectra were computed according to the formalism described in ref. 24, 29 and 30. The intensities of the infrared absorption spectrum of the transverse optical phonons having frequencies ωT at the Brillouin zone center take on the form:  where κ is the refractive index, Z* denotes the Born dynamical charge tensor, and j runs over the vibrational modes. Details of the calculations can also be found elsewhere.31,32
where κ is the refractive index, Z* denotes the Born dynamical charge tensor, and j runs over the vibrational modes. Details of the calculations can also be found elsewhere.31,32
3 Results and discussion
3.1 Structural and magnetic properties
The parameters of the TlCo2Se2 structure calculated at the ground state together with the results of the neutron diffraction measurements of powder14 and single-crystalline samples15 are summarized in Table 1. The optimized lattice constants (a, c) and the zSe coordinate of the selenium atom closely correspond to those determined in the most recent experiments on TlCo2Se2 (ref. 14 and 15) and TlCo2Se2−xSx (ref. 17) with x = 0 as well as to those determined in earlier experiments on Tl1−xKxCo2Se2 (ref. 6) and TlCo2−xNixSe2 (ref. 9) at x = 0. The largest deviation between the results of our DFT calculations and the experimental data (∼2.5%) was observed for the c lattice constant. This affects the interlayer distance dinterCo–Co which is overestimated in comparison with the results of measurements by the same amount. On the other hand, the difference between the calculated and experimental lattice constant a, which is below 1%, has a negligible effect on the intralayer Co–Co distance dintraCo–Co. The remaining interatomic distances i.e. dCo–Se, dSe–Se, dTl–Co, and dTl–Se, which also depend on zSe, correlate with the experimental results within ∼1%.| Quantity | Present | 10 K | 45 K |
|---|---|---|---|
| a (Å) | 3.8265 | 3.8316 | 3.8315 |
| c (Å) | 13.7612 | 13.4254 | 13.4400 |
| zSe | 0.3471 | 0.3537 | 0.3537 |
| dintraCo–Co (Å) | 2.7057 | 2.7094 | 2.7093 |
| dinterCo–Co (Å) | 6.8806 | 6.7127 | 6.7200 |
| dCo–Se (Å) | 2.3337 | 2.3682 | 2.3691 |
| dSe–Se (Å) | 3.8030 | 3.8851 | 3.8872 |
| dTl–Co (Å) | 3.9365 | 3.8646 | 3.8678 |
| dTl–Se (Å) | 3.4276 | 3.3464 | 3.3476 |
| M (μB) | 0.78 | 0.46 | 0.70 |
| qz | 0.337 | 0.324 | 0.309 |
| Θ | 119.4 | 121.7 | 124.4 |
The calculated helical arrangement of spin is characterized by the propagating vector q = (0, 0, qz) with qz = 0.337 and the corresponding helical turn angle between the two adjacent planes containing Co ions Θ = 119.4°. Both theoretical values remain in quite good agreement with the respective experimental data14,15 (see Table 1) and the results16 for the linear muffin-tin orbital method implementing atomic spheres approximation (LMTO-ASA) which gives qz = 0.287 and Θ = 128.3°. There is, however, significant discrepancy between the magnetic moment on the Co ion gained from the present work (M = 0.78 μB) and that deduced14 from the neutron powder diffraction (NPD) experiments (0.46 μB). We note that significantly higher M = 0.72 μB has also been obtained in the LMTO-ASA calculations.16 On the contrary, both theoretical approaches produce magnetic moments conforming to the results of the neutron diffraction measurements on single-crystalline15,16 TlCo2Se2 which yield M = 0.7 μB. We should mention that, a too low value of M found in the NPD experiments can result from weak magnetic contributions (low intensities of the magnetic peaks) to the powder diffraction pattern.14 Thus, the neutron diffraction of TlCo2Se2 single-crystals seems to provide more reliable values for the magnetic moments of Co ions as compared to the NPD experiments, this is also because the latter technique is unable to give sufficient spatial information.15
A non-commensurate helical magnetic structure with qz ∼ 0.3 was shown to be more stable than both the ferromagnetic and antiferromagnetic solutions within the LMTO-ASA first principles calculations.16 Unfortunately, this result has not been confirmed by the full-potential augmented plane wave method (FP-APW + lo), in which the antiferromagnetic state minimizes the energy of the TlCo2Se2 system.15 Therefore, we have performed additional calculations for the system with the interlayer AF order and intralayer FM alignment of the Co spins, as suggested by some early experiments.6,9 The calculated difference in energies between the TlCo2Se2 structure with the AF ordering of Co spins and the structure with Co spins conforming to the helical magnetic order ΔE0 = EAF0 − EHLX0 amounts to 0.29 meV per formula unit (f.u.), indicating that the former is less energetically favourable than the latter one. Furthermore, the helical magnetic structure is additionally stabilized by phonons as the difference in the energies ΔE = ΔE0 + ΔEvib, which takes into account the zero-point energy motions of the respective lattices ΔEvib = EAFvib − EHLXvib, becomes equal to 5.9 meV per f.u.
3.2 Phonon spectra
Fig. 2 displays the total and atomic-projected phonon densities of the states calculated for the helical magnetic structure of TlCo2Se2. The phonon spectrum which covers the frequency range up to about 33 meV can be divided into three bands. The lowest band (I) extends to about 10 meV and remains dominated by the vibrations of the Tl-sublattice, while the phonons associated with vibrations of the Co- and Se-sublattices are only a small admixture in this band. The bottom of band I corresponds mostly to the acoustic phonon modes, whereas the top of this band is constituted by the low-lying transverse optical (TO) modes. | ||
| Fig. 2 (a) Total phonon density of states and (b) partial densities of phonon states for the Tl, Co, and Se sublattices in TlCo2Se2 with helical magnetic structure. | ||
Both the middle and the highest-frequency bands, which range respectively from 10 meV to 22 meV (band II) and from 22 meV to 33 meV (band III) are solely due to mixed vibrations of the Co and Se atoms within the CoSe4 tetrahedral units. Transverse optical phonon modes are the main constituents of the band II. This band remains dominated by two intense peaks, both originating from vibrations of the Se and Co atoms along the c-axis i.e. in the direction perpendicular to the Co–Se layers, with the lower (higher) frequency peak arising from movements of Se (Co) atoms. Here, the phonon peaks resulting from atomic displacements within the Co–Se layers are significantly smaller in comparison with those perpendicular to the layers. Vibrations of the Co and Se atoms within the layers become enhanced in band III and they give rise to the high-frequency transverse and longitudinal optic (LO) modes. The LO phonons set up the top of band III.
The location of phonon bands in TlCo2Se2 is very similar to that found for its ferromagnetic counterpart31 KCo2Se2, nevertheless the phonons of the Tl-sublattice belong to band I, while phonons of the K-sublattices are confined to band II. In both of the Co-based ternary dichalcogenides no gap separating the middle-frequency band II from the high-frequency band III exists, unlike that in the Pauli paramagnetic KNi2Se2 (with negligible effective magnetic moment on the Ni-sublattice) where a small gap (∼2.5 meV) appears.32 Such a difference between the FM (or AF) compounds and the paramagnetic one is due to the spin–phonon interaction affecting the atomic bonding, and hence the force constants which determine the phonon dynamics of particular systems. We should mention that the spin–phonon interaction has a meaningful impact on the phonon frequencies, as was shown33 for the antiferromagnetic Fe-based ternary dichalcogenides KFe2Se2 or KxFe2ySe2.
The phonon DOS can be used to determine the Debye temperature (ΘD) of the TlCo2Se2 compound by applying the relationship:34 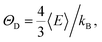 where kB is the Boltzmann constant, E = ℏω, and
where kB is the Boltzmann constant, E = ℏω, and  with g(E) denoting the total phonon density of states. The resulted ΘD = 135 K.
with g(E) denoting the total phonon density of states. The resulted ΘD = 135 K.
The phonon spectrum of TlCo2Se2 can be measured by inelastic neutron scattering (INS) experiments. However, a direct comparison of the calculated and the INS spectra requires evaluation of the so-called generalized phonon density of states (GDOS) i.e. the quantity which is usually extracted from the measured scattering function.33 The GDOS differs from the bare phonon DOS because of different scattering efficiencies (σ/M) of the atomic species constituting particular sublattices of a system.35 Here, σ and M are the total scattering cross section and atomic mass, respectively. For TlCo2Se2 the weighting factors amount to36 0.048 barn per a.m.u. for Tl, 0.095 barn per a.m.u. for Co, and 0.105 barn per a.m.u. for Se. Thus, the GDOS obtained according to relation:  with ci and gi(ω) denoting respectively the concentration and partial phonon DOS of the i-th atom, represents predominantly the dynamics of the Co–Se layers. This results from particular contributions to the GDOS spectrum which amount to 42% for Co, 47% for Se and 11% for Tl sublattices. Therefore, a somewhat different INS experimental spectrum of band I should be expected because the high-intensity peaks yielded by vibrations of the Tl-sublattice would be considerably suppressed in comparison to those shown in Fig. 2.
with ci and gi(ω) denoting respectively the concentration and partial phonon DOS of the i-th atom, represents predominantly the dynamics of the Co–Se layers. This results from particular contributions to the GDOS spectrum which amount to 42% for Co, 47% for Se and 11% for Tl sublattices. Therefore, a somewhat different INS experimental spectrum of band I should be expected because the high-intensity peaks yielded by vibrations of the Tl-sublattice would be considerably suppressed in comparison to those shown in Fig. 2.
3.3 Raman and infrared spectra
The primitive unit cell of the AT2X2 (TlCo2Se2) compound with the space group I4/mmm contains 5 atoms, and hence 15 phonon branches are expected for an arbitrary wave vector q. A factor group analysis also provides 15 modes at the Brillouin zone center. The zone-center phonon modes can be decomposed into the irreducible representations of the point group D174h as follows: A1g ⊕ B1g ⊕ 2E(II)g ⊕ 3A2u ⊕ 3E(II)u. Among them 3 modes (A2u ⊕ E(II)u) are lattice translational modes. Because of the presence of the inversion symmetry the modes are either Raman-active (gerade) or infrared (IR)-active (ungerade). The modes with symmetries A1g, B1g, and Eg are Raman-active, whereas modes A2u and Eu are IR-active. The Eg and Eu remain doubly degenerate. There are no optically inactive (silent) modes at the Γ-point. Contributions of particular atomic sites to the zone-center phonons of the AT2X2 system are given in Table 2.| Atomic site | Irrep. |
|---|---|
| A (2a) | A2u ⊕ Eu |
| T (4d) | A2u ⊕ B1g ⊕ Eg ⊕ Eu |
| X (4e) | A1g ⊕ A2u ⊕ Eg ⊕ Eu |
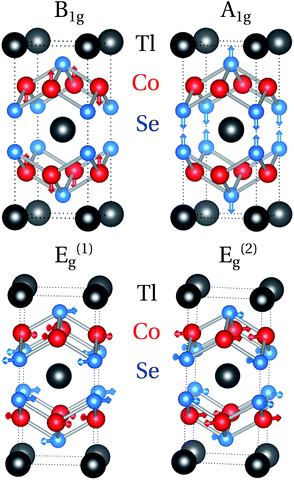
In the Raman-active modes the A (Tl) ions are at rest as they are located at inversion centers. The A1g and B1g phonons involve vibrations of the T (Co)- and X (Se)-sublattices along the crystallographic c-axis, while vibrations of these sublattices within the tetragonal ab-plane give rise to the Eg modes, as schematically illustrated in Fig. 3. We may regard the phonons with symmetries of A1g and B1g as the breathing modes, whereas the Eg phonons as interlayer shear modes. The frequencies of particular Raman phonon modes predicted by our calculations for TlCo2Se2 are as follows: ω(E(1)g) = 13.77, ω(B1g) = 19.88, ω(A1g) = 25.66, ω(E(2)g) = 31.42 meV.
The Raman tensors for the particular phonon modes in the AT2X2 system have only the following non-zero components:
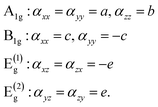 | (1) |
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ], ki = [010] and ks = [0
], ki = [010] and ks = [0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] or ki = [100] and ks = [
0] or ki = [100] and ks = [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00]), the mode of A1g symmetry always appears in the polarized backscattering Raman spectra when the incident light polarization vector (ei) and the scattered light polarization vector (es) are parallel (ei ∥ es), while it disappears for the crossed polarization configuration (ei ⊥ es). The intensity of this mode depends on the angle ϕ between ei and es i.e. I(A1g) ∝ |a|2
00]), the mode of A1g symmetry always appears in the polarized backscattering Raman spectra when the incident light polarization vector (ei) and the scattered light polarization vector (es) are parallel (ei ∥ es), while it disappears for the crossed polarization configuration (ei ⊥ es). The intensity of this mode depends on the angle ϕ between ei and es i.e. I(A1g) ∝ |a|2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2
cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. However, in the parallel polarization configuration, such as ei ∥ x, where x = [100] is the crystal axis (for example z(xx)
θ. However, in the parallel polarization configuration, such as ei ∥ x, where x = [100] is the crystal axis (for example z(xx)![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) or y(xx)
or y(xx)![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) in Porto’s notation), the A1g mode is assisted by the B1g mode, the latter having an intensity dependent not only on the ϕ angle but also on the sample orientation defined by the angle ψ = ∠(ei,x). The intensity of the B1g phonon is given as I(B1g) ∝ |c|2
in Porto’s notation), the A1g mode is assisted by the B1g mode, the latter having an intensity dependent not only on the ϕ angle but also on the sample orientation defined by the angle ψ = ∠(ei,x). The intensity of the B1g phonon is given as I(B1g) ∝ |c|2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ϕ + 2ψ). Therefore, in the parallel polarization configuration (ϕ = 0) and sample orientation ψ = 0 (ei ∥ x), I(B1g) is maximum, as shown in Fig. 4. At this scattering geometry, the I(A1g) is constant and treated here as the scaling factor, while the I(B1g) gradually decreases with increasing ψ and reaches null value at ψ = 45°. The calculated intensity ratio I(B1g)/I(A1g) = 1.376 for ψ = 0 in the parallel polarization configuration. An opposite behavior of the I(B1g) is observed in the crossed polarization configuration (ϕ = 90°), where I(B1g) gradually increases with increasing ψ and becomes maximal at ψ = 45°.
cos(ϕ + 2ψ). Therefore, in the parallel polarization configuration (ϕ = 0) and sample orientation ψ = 0 (ei ∥ x), I(B1g) is maximum, as shown in Fig. 4. At this scattering geometry, the I(A1g) is constant and treated here as the scaling factor, while the I(B1g) gradually decreases with increasing ψ and reaches null value at ψ = 45°. The calculated intensity ratio I(B1g)/I(A1g) = 1.376 for ψ = 0 in the parallel polarization configuration. An opposite behavior of the I(B1g) is observed in the crossed polarization configuration (ϕ = 90°), where I(B1g) gradually increases with increasing ψ and becomes maximal at ψ = 45°.
The A1g mode can be the only mode detected in the Raman spectrum measured at the y(zz)ȳ scattering geometry. One may also observe a single peak associated with the A1g phonon by performing measurements from the crystal ab-plane, but such a configuration requires setting the incident light polarization along the 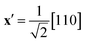 crystal axis, and then one may work with the z(x′x′)
crystal axis, and then one may work with the z(x′x′)![[z with combining macron]](https://www.rsc.org/images/entities/b_char_007a_0304.gif) scattering geometry. The Raman spectrum can also reveal a single phonon peak due to the B1g mode in the crossed polarization configuration, such as z(x′y′)
scattering geometry. The Raman spectrum can also reveal a single phonon peak due to the B1g mode in the crossed polarization configuration, such as z(x′y′)![[z with combining macron]](https://www.rsc.org/images/entities/b_char_007a_0304.gif) , where
, where  Determination of the Eg symmetry phonon modes is possible when the Raman scattering measurements are carried out for the crystal ac-plane and a crossed polarization configuration, e.g. y(zx)ȳ scattering geometry.
Determination of the Eg symmetry phonon modes is possible when the Raman scattering measurements are carried out for the crystal ac-plane and a crossed polarization configuration, e.g. y(zx)ȳ scattering geometry.
Typical polarized Raman spectra of the TlCo2Se2 crystal simulated at the scattering configurations z(xx)![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) and y(zx)ȳ are displayed in Fig. 5. The spectrum calculated at scattering geometry z(xx)
and y(zx)ȳ are displayed in Fig. 5. The spectrum calculated at scattering geometry z(xx)![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) shows two peaks which are attributed to the phonons with the B1g symmetry (19.88 meV) and A1g symmetry (25.66 meV). In TlCo2Se2 the B1g phonon mode is more intense than the A1g, whereas opposite effects are encountered in the ferromagnetic31 KCo2Se2 and paramagnetic32,38 KNi2Se2, where the phonons of B1g symmetries exhibit significantly lower intensities as compared to the phonons of A1g symmetries. The E(1)g (13.77 meV) and E(2)g (31.42 meV) which can be observed in the Raman spectrum of TlCo2Se2 at the y(zx)ȳ scattering geometry are shown to have lower and higher intensities, respectively, and the intensity ratio I(E(1)g)/I(E(2)g) ∼ 0.24. However, for the ferromagnetic KCo2Se2 compound the intensity ratio of the E(1)g and E(2)g modes is almost null, and hence its Raman scattering spectrum is characterized31 by a single peak arising from the higher frequency E(2)g phonon mode. On the other hand, the E(2)g mode is hardly observed in the Raman spectrum of the paramagnetic KNi2Se2 due to its low intensity and the spectrum shows a single peak resulting from the quite intense E(1)g mode having a lower frequency.32,38
shows two peaks which are attributed to the phonons with the B1g symmetry (19.88 meV) and A1g symmetry (25.66 meV). In TlCo2Se2 the B1g phonon mode is more intense than the A1g, whereas opposite effects are encountered in the ferromagnetic31 KCo2Se2 and paramagnetic32,38 KNi2Se2, where the phonons of B1g symmetries exhibit significantly lower intensities as compared to the phonons of A1g symmetries. The E(1)g (13.77 meV) and E(2)g (31.42 meV) which can be observed in the Raman spectrum of TlCo2Se2 at the y(zx)ȳ scattering geometry are shown to have lower and higher intensities, respectively, and the intensity ratio I(E(1)g)/I(E(2)g) ∼ 0.24. However, for the ferromagnetic KCo2Se2 compound the intensity ratio of the E(1)g and E(2)g modes is almost null, and hence its Raman scattering spectrum is characterized31 by a single peak arising from the higher frequency E(2)g phonon mode. On the other hand, the E(2)g mode is hardly observed in the Raman spectrum of the paramagnetic KNi2Se2 due to its low intensity and the spectrum shows a single peak resulting from the quite intense E(1)g mode having a lower frequency.32,38
The unpolarized Raman scattering spectrum calculated from the crystal ab-plane as well as the backscattering spectrum of the polycrystalline TlCo2Se2 (not shown) reveal two-peak structures originating from the B1g and A1g phonons. The I(B1g)/I(A1g) for monocrystalline and polycrystalline systems equal about 1.8 and 1.2, respectively. Although both Eg modes are also present in these spectra, they have incomparably weaker intensities compared to the strong B1g and A1g modes, and thus they are not expected to be detected experimentally.
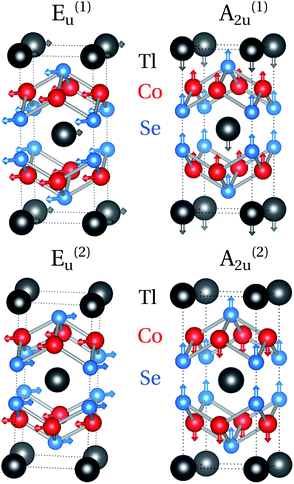
In the AT2X2 system, the infrared active phonons of A2u and Eu symmetries correspond to the oscillations of the dipole moment along and perpendicular to the T–X layers, respectively. These modes are schematically presented in Fig. 6. The respective frequencies of the IR-active modes for the TlCo2Se2 compound are as follows: ω(E(1)u) = 5.20, ω(A(1)2u) = 5.92, ω(E(2)u) = 30.29, ω(A(2)2u) = 31.98 meV. The A2u and Eu modes can be observed in the IR absorption spectra when the incident radiation E is parallel and perpendicular to the crystallographic c-axis.
In order to calculate the intensities of the absorption peaks associated with the transverse optical phonons of the A2u and Eu symmetries, one needs to determine components of the Born effective charge (Z*) and dielectric (ε) tensors. In TlCo2Se2, both tensors consist of two independent components which are perpendicular and parallel to the crystal c-axis i.e.  and (ε⊥, ε∥). Our computations produce ε (401.41, 93.95) and the Born dynamical charges of particular atomic species as follows:
and (ε⊥, ε∥). Our computations produce ε (401.41, 93.95) and the Born dynamical charges of particular atomic species as follows: 
 and
and  The anisotropy between ε⊥ and ε∥ is about two times larger in TlCo2Se2 than in KCo2Se2, which is mainly due to the fact that the value of ε∥ for TlCo2Se2 is more than two times smaller than that for KCo2Se2.31 Nevertheless, the structural features of these two ternary transition-metal dichalcogenides are similar, they exhibit a reversed relation between the perpendicular and parallel components of the Z* tensors. In TlCo2Se2 we found
The anisotropy between ε⊥ and ε∥ is about two times larger in TlCo2Se2 than in KCo2Se2, which is mainly due to the fact that the value of ε∥ for TlCo2Se2 is more than two times smaller than that for KCo2Se2.31 Nevertheless, the structural features of these two ternary transition-metal dichalcogenides are similar, they exhibit a reversed relation between the perpendicular and parallel components of the Z* tensors. In TlCo2Se2 we found  for Co and Se ions and
for Co and Se ions and  for Tl ions, while in KCo2Se2 the respective relations are completely opposite. This effect may result from the magnetic interactions which are antiferromagnetic in TlCo2Se2 and ferromagnetic in KCo2Se2, but it has a negligible influence on the simulated IR absorption spectra which are found to be quite similar for both compounds.
for Tl ions, while in KCo2Se2 the respective relations are completely opposite. This effect may result from the magnetic interactions which are antiferromagnetic in TlCo2Se2 and ferromagnetic in KCo2Se2, but it has a negligible influence on the simulated IR absorption spectra which are found to be quite similar for both compounds.
The absorption spectrum of TlCo2Se2 (see Fig. 7), likewise that of KCo2Se2 displays small intensity A(1)2u and E(1)u peaks and high intensity A(2)2u and E(2)u peaks, independently of the scattering configuration. The strong A(2)2u and E(2)u peaks are almost ten times higher than the weak A(1)2u and E(1)u peaks. On the other hand, the unpolarized IR absorption spectra of either monocrystalline or polycrystalline TlCo2Se2 systems contain all of the IR-active modes, but only the Eu ones have intensities large enough for detection in experiments. Again, the absorption peak of the lower frequency E(1)u mode is about eight times smaller than the absorption peak of the higher frequency E(2)u mode.
4 Summary and conclusions
The present work reports on the structural, magnetic and dynamical properties of the quasi-2D layered ternary transition metal dichalcogenide TlCo2Se2 with helical magnetic ordering. Results of the present theoretical research based on the DFT method indicate that the structure, with a spin spiral characterized by a propagation wave vector (0, 0, 0.337) and a turn angle of 119°, is more energetically stable than the structure with a conventional AF order of type-I. Moreover, the helical magnetic order of TlCo2Se2 is additionally stabilized by phonons which increases the energy difference between structures with helical and AF magnetic order. The phonon spectra determined from inelastic neutron scattering experiments are expected to provide information on atomic vibrations within and perpendicular to the Co–Se layers. The predicted Raman and IR absorption spectra which were analyzed in terms of the I4/mmm space group symmetries are supposed to reflect magnetic interactions within the Co–Se layers, where the spin–phonon coupling seems to be quite strong. Results of our theoretical studies could be useful for the interpretation of TlCo2Se2 spectra measured in future INS, Raman and IR experiments.Acknowledgements
Interdisciplinary Center for Mathematical and Computational Modeling (ICM), Warsaw University, Poland and the IT4Innovations National Supercomputing Center, VSB-Technical University, Ostrava, Czech Republic are acknowledged for providing the computer facilities under Grants No. G28-12 and LM2015070.References
- A. L. Ivanovskii, Phys. C, 2011, 471, 409 CrossRef CAS.
- H.-H. Wen, Rep. Prog. Phys., 2012, 75, 112501 CrossRef PubMed.
- J. R. Neilson, A. Llobet, A. V. Stier, L. Wu, J. Wen, J. Tao, Y. Zhu, Z. B. Tesanovic, N. P. Armitage and T. M. McQueen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 054512 CrossRef.
- J. R. Neilson and T. M. McQueen, J. Am. Chem. Soc., 2012, 134, 7750 CrossRef CAS PubMed.
- J. R. Neilson, T. M. McQueen, A. Llobet, J. Wen and M. R. Suchomel, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 045124 CrossRef.
- G. Huan and M. Greenblatt, J. Less-Common Met., 1989, 156, 247 CrossRef CAS.
- G. Huan, M. Greenblatt and K. V. Ramanujachary, Solid State Commun., 1989, 71, 221 CrossRef CAS.
- G. Huan, M. Greenblatt and M. Croft, Eur. J. Solid State Inorg. Chem., 1989, 26, 193 CAS.
- A. R. Newmark, G. Huan, M. Greenblatt and M. Croft, Solid State Commun., 1989, 71, 1025 CrossRef CAS.
- S. Ronneteg, M. W. Lumey, R. Dronskowski, U. Gelius, R. Berger, S. Felton and P. Nordblad, J. Solid State Chem., 2004, 177, 2977 CrossRef CAS.
- M. Oledzka, J.-G. Lee, K. V. Ramanujachary and M. Greenblatt, J. Solid State Chem., 1996, 127, 151 CrossRef CAS.
- Y. Yang, B. Chen, H. Wang, Q. Mao, M. Imai, K. Yoshimura and M. Fang, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 064406 CrossRef.
- F. von Rohr, A. Krzton-Maziopa, V. Pomjakushin, H. Grundmann, Z. Guguchia, W. Schnick and A. Schilling, J. Phys.: Condens. Matter, 2016, 28, 276001 CrossRef PubMed.
- R. Berger, M. Fritzsche, A. Broddefalk, P. Nordblad and B. Malaman, J. Alloys Compd., 2002, 343, 186 CrossRef CAS.
- R. Lizárraga, S. Ronneteg, R. Berger, A. Bergman, P. Mohn, O. Eriksson and L. Nordström, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 024407 CrossRef.
- R. Lizárraga, S. Ronneteg, R. Berger, P. Mohn, L. Nordström and O. Eriksson, J. Magn. Magn. Mater., 2004, 272–276, 557 CrossRef.
- S. Ronneteg, S. Felton, R. Berger and P. Nordblad, J. Magn. Magn. Mater., 2006, 299, 53 CrossRef CAS.
- S. Ronneteg, M. Lumey, R. Dronskowski and R. Berger, J. Magn. Magn. Mater., 2006, 303, 204 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- K. Parlinski, Z.-Q. Li and Y. Kawazoe, Phys. Rev. Lett., 1997, 78, 4063 CrossRef CAS.
- K. Parlinski, Software PHONON ver. 6.15, Cracow, Poland, 2015 Search PubMed.
- Light Scattering in Solids I, Topics in Applied Physics, ed. M. Cardona, Springer-Verlag, Berlin, 1983, vol. 8 Search PubMed.
- P. Umari, A. Pasquarello and A. Dal Corso, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 094305 CrossRef.
- P. Umari, X. Gonze and A. Pasquarello, Phys. Rev. Lett., 2003, 90, 027401 CrossRef CAS PubMed.
- M. Gajdoŝ, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045112 CrossRef.
- F. Giustino and A. Pasquarello, Phys. Rev. Lett., 2005, 95, 187402 CrossRef PubMed.
- F. Giustino and A. Pasquarello, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 075307 CrossRef.
- U. D. Wdowik, G. Jagło and P. Piekarz, J. Phys.: Condens. Matter, 2015, 27, 415403 CrossRef PubMed.
- G. Jagło, M. Mȩdala and U. D. Wdowik, Phys. Lett. A, 2015, 379, 183 CrossRef.
- R. Mittal, M. K. Gupta, S. L. Chaplot, M. Zbiri, S. Rols, H. Schober, Y. Su, T. Brueckel and T. Wolf, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184502 CrossRef.
- G. Grimvall, Thermophysical Properties of Materials, North-Holland, Amsterdam, 1999 Search PubMed.
- S. W. Lovesey, Theory of Neutron Scattering from Condensed Matter, Oxford University Press, Oxford, 1987 Search PubMed.
- V. Sears, Neutron News, 1992, 3, 26 CrossRef.
- R. Loudon, Adv. Phys., 2001, 50, 813 CrossRef.
- N. Lazarević, M. Radonjić, M. Šćepanović, H. Lei, D. Tanasković, C. Petrovic and Z. V. Popović, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 144305 CrossRef.
| This journal is © The Royal Society of Chemistry 2016 |