Steering the formation of supported Pt–Sn nanoalloys by reactive metal–oxide interaction
Abstract
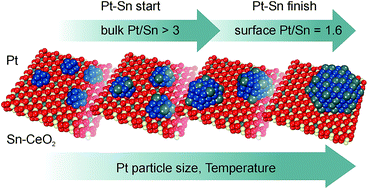
The formation of a supported Pt–Sn nanoalloy upon reactive metal–oxide interaction between Pt nanoparticles and a Sn–CeO2 substrate has been investigated by means of synchrotron radiation photoelectron spectroscopy and resonant photoemission spectroscopy in combination with density functional modeling. It was found that Pt deposition onto a Sn–CeO2 substrate triggers the reduction of Sn2+ cations yielding Pt–Sn nanoalloys at 300 K under ultra-high vacuum conditions. Three distinct stages of Pt–Sn nanoalloy formation were identified associated with the growth of (I) ultra-small monometallic Pt particles on a Sn–CeO2 substrate, (II) Pt–Sn nanoalloys on a Sn–CeO2 substrate, and (III) Pt–Sn nanoalloys on a stoichiometric CeO2 substrate. These findings suggest the existence of a critical size of monometallic Pt particles above which the formation of a Pt–Sn nanoalloy becomes favorable. In this respect, density functional modeling revealed a strong dependence of the formation energy of the PtxSn nanoalloy on the size of the Pt particle. Additionally, the thermodynamically favorable bulk and surface Pt/Sn stoichiometries were identified as two parameters that determine the composition of the supported Pt–Sn nanoalloys and limit the extraction of Sn2+ from the Sn–CeO2 substrate. Primarily, the formation of a bulk Pt3Sn alloy phase drives the growth of the Pt–Sn nanoalloy upon Pt deposition at 300 K. Upon annealing, Sn segregation on the surface of the Pt–Sn nanoalloy promotes further extraction of Sn2+ until the thermodynamically stable Pt/Sn concentration ratios of 3 for the bulk and approximately 1.6 for the surface are reached.


 Please wait while we load your content...
Please wait while we load your content...