Concentration-induced structural transition of block polymer self-assemblies on a nanoparticle surface: computer simulation

Abstract

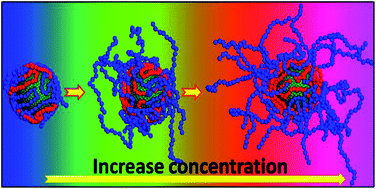
Coarse-grained molecular dynamic simulation (CGMD) techniques are used to study the self-assembly behavior of Pluronic triblock copolymers on different hydrophobicity nanoparticle (NP) surfaces. The structural changeover as a function of concentration of Pluronic triblock copolymers is investigated. At lower concentration (e.g. 5%), a shell-layered film structure self-assembled on NP surfaces is observed. Above 5%, the stretching growth of polymer chains takes place during the adsorption process and the star-shaped film on NP surfaces is formed. As the simulation results show, the radius of gyration of F127 assembled on the NPs would increase with increase of polymer concentration. A transition from incomplete to complete stretching polymer chain structure growth in solvent is encountered with increasing concentrations, which appears as a high phase separation film in terms of order parameter. These changes of the self-assembled films are not majorly initiated by the hydrophobic degrees of NP surfaces, but originate from the domination of polymer concentration.

---

1. Introduction

The assembly of complex structures out of simple colloidal building blocks is of practical interest for building materials with unique material properties (for example adhesive properties, lubricants, membranes, and coatings)^1–3 and is of fundamental importance in improving our understanding of self-assembly processes occurring at molecular or macroscopic length scales.⁴ There has been growing interest in the preparation of different kinds of colloidal nanoparticles (NPs) with controlled structure and shape.^5,6 A variety of NP complex structures with amphiphilic molecules, such as ‘lock-key’, ‘flowers’, ‘star-like’ and ‘rod-like’ structures, has been found to date.^7–10 Block copolymers (like Pluronic copolymers), have been regarded as important film modifiers of colloidal NP surfaces by physical adsorption.¹¹ This is in part due to their amphiphilic features that endow molecular constructs with tailorable surfaces affinities, depending on the adsorbing surfaces and the surrounding medium.¹² Compared with hydrophilic surfaces, there are stronger interactions between hydrophobic surfaces and block copolymers.^13,14

Using block copolymers has been proved to be an efficient approach to precisely control the properties of NPs complex. Toshio Sakai et al.¹⁵ studied the gold NPs growth and size control in aqueous Pluronic triblock copolymers solutions. The poly(propylene oxide)–poly(ethylene oxide)–poly(propylene oxide) (PEO–PPO–PEO) block copolymers could result into the formation of silica nanospheres vesicular assembly. Moreover, the size of silica NP vesicles can be tuned by changing these triblock copolymers molecular weight.¹⁶ Agrawal et al.¹⁷ used small-angle X-ray scattering and dynamic light scattering find that NPs in poly(lactide)–poly(ethylene oxide)–poly(lactide) (PLA–PEO–PLA) solutions could increase the intermicellar attraction and lead to reinforced associative network hydrogels. Furthermore, the formation of selectively hydrogen bond between NPs and one of the segments of a block copolymer could induce more order colloidal systems.¹⁸ This enables the fabrication of well-ordered hybrid materials with spherical, cylindrical, or lamellar. The temperature-responsive properties of magnetite/polymer nanoparticles were investigated by Chen et al.¹⁹ The temperature-induced self-assembly of the immobilized block copolymers adsorbed on the magnetite solid surfaces was observed, this process is accompanied by a conformational transition from a fully extended state to a highly coiled state of the copolymer. To the best of our knowledge, no such studies have been made so far to reveal the films structure of asymmetric triblock copolymer assembled on different hydrophobicity of nanoparticle surfaces using coarse-grained molecular dynamic (CGMD) simulations.

As a rapid development research method, CGMD simulations can provide specific information regarding the assembly behavior of PEO–PPO–PEO triblock copolymers on hydrophobic nanoparticle surfaces without compromising the molecular details.²⁰ What's more, the coarse-grained molecular dynamic simulations have been applied to investigate various kinds of polymers and NP systems.^21–23 F127 (EO₂₃PO₂₁EO₂₃) is an amphiphilic non-ionic surfactant of the more general class of copolymers known as Pluronic polymer. The molecular weight of Pluronic F127 was 12 600 g mol⁻¹ and the mole ratio of EO in Pluronic F127 was 68.66%. It has received increasing attention as a modifier of solid surfaces. In this work, we demonstrate that the structure of self-assembled films made of highly asymmetric F127 copolymer on different hydrophobicity of nanoparticle surfaces, and these films structure can be tuned by varying the concentration of polymer solutions.

2. Methodology

2.1 Force field parameterization

The CG force field known as MARTINI is a thermodynamic based coarse-grain model.²⁴ It was originally developed specifically for phospholipids forming biological membranes,²⁵ but was later extended to model other biological and chemical systems such as DNA,²⁶ polystyrene brush,²⁷ and NPs.²⁸ The MARTINI force field includes four main types of interaction sites: polar (P), nonpolar (N), apolar (C), and charged (Q), and each had a number of subtypes (represented by subscripts) allowing for more accurate representations of chemical structures.²⁹ Based on an atomistic molecular dynamics model, the model parameter for the polymers and water was optimized by Samira Hezaveh et al.^30,31 In this paper, we assumed the NPs had a strong repulsive interaction with aqueous phase while had a strong attractive interaction with Pluronic copolymers.^13,32 These parameters including none-bonded and bonded interactions were qualitatively in good agreement with published experimental data which could be found in Tables 1 and 2.^31,33,34 The nonbonded interactions were Lennard-Jones 6–12 forces with a 12.5 Å cutoff. The bonded interactions consist of the harmonic bond stretching forces, harmonic angle bending forces. As shown in Table 3, there were various interaction types of Lennard-Jones (LJ) parameters in MARTINI force field, such as super attractive, attractive, super repulsive, repulsive, intermediate et al.³⁵ Based on different of attractive and repulsive LJ parameter models, the interactions between polymer and different hydrophobicity of nanoparticle surfaces were provided in this paper, as shown in Table 4. For the interactions between EO and NPs, we chose four types of different repulsive interactions LJ model including super repulsive, repulsive, almost repulsive and almost intermedia. Meanwhile, four types of different attractive interactions LJ model were provided for PO and NPs including super attractive, attractive, almost attractive and intermedia. Correspondingly, four types hydrophobic nanoparticle surfaces were defined such as SS model (super attractive–super repulsive), AR model (attractive–repulsive), AA model (almost attractive–almost repulsive) and IA model (intermediate–almost intermediate). More details of four types of hydrophobic nanoparticle surfaces could be found in Table 4. The hydrophobic degree was SS model > AR model > AA model > IA model. The mapping scheme for polymer and NPs was sketched in Fig. 1. The NPs simulated in our system were consists of 760 small NP beads whose diameter was 19.6 nm. The spherical coordinates was generated by following equations: x = r sin(θ)cos(ϕ), y = r sin(θ)sin(ϕ), z = r cos(θ), where θ is polar angle, ϕ is azimuthal angle.³⁶ The mapping scheme for the Pluronic F127 chain considered the EO and PO monomers as a single particle, respectively. Three water molecules were coarse-grained as one bead.^31,33

Table 1 Parameters for the bonded interactions for CG Pluronic^30a

	Bond		Angle
	b0 (nm)	Kb (kJ mol^−1 nm^−2)	θ0	Kθ (kJ mol^−1)
a The functions employed to model the stretching (Vbond) and bending (Vangle) potentials are Vbond(b) = (1/2)Kb(b − b0)^2 and Vangle(θ) = (1/2)Kθ(cos(θ) − cos(θ0)).^2
PEO–PEO	0.28	8000	155	40
PPO–PPO	0.28	5000	140	40

---

Table 2 Non-bonded interactions for CG Pluronic beads^30,31

Type	σ (nm)	ε (kJ mol^−1)
EO–EO	0.48	3.5
PO–PO	0.5	2.6
EO–PO	0.47	2.9
W–W	0.47	5.0
EO–W	0.47	4.5
PO–W	0.47	3.5
NPs–W	0.47	2.0

---

Table 3 LJ parameters for different interaction types in MARTINI force field^33–35a

Interaction type	ε (kJ mol^−1)	σ (nm)
a The functions employed to model the van der Waals interactions are presented by a Lennard-Jones (LJ) potential function: .
Super attractive	5.6	0.47
Attractive	5.0	0.47
Almost attractive	4.5	0.47
Semi attractive	4.0	0.47
Intermediate	3.5	0.47
Almost intermediate	3.1	0.47
Semi repulsive	2.7	0.47
Almost repulsive	2.3	0.47
Repulsive	2.0	0.47
Super repulsive	2.0	0.62

---

Table 4 Non-bonded interactions for CG Pluronic and nanoparticles (NPs) beads

Type	ε (kJ mol^−1)	σ (nm)	Interaction type	Description
NPs–EO	5.6	0.47	Super repulsive	SS model
NPs–PO	5.0	0.47	Super attractive
NPs–EO	4.5	0.47	Repulsive	AR model
NPs–PO	4.0	0.47	Attractive
NPs–EO	3.5	0.47	Almost repulsive	AA model
NPs–PO	3.1	0.47	Almost attractive
NPs–EO	2.7	0.47	Almost intermediate	IA model
NPs–PO	2.3	0.47	Intermediate

---

Fig. 1 Schematic of one simulated system. A biphasic system containing solvent (water), NP and PEO–PPO–PEO triblock copolymer (F127) is considered. Pink and green beads represent water (W) and nanoparticle (NP), respectively. The NP simulated in system is consists of 760 small NP beads with diameter is 19.6 nm. Blue and red beads indicate ethylene oxide (EO) and propylene oxide (PO) of F127 triblock copolymers, respectively.

2.2 Simulation setup

The CGMD simulations were carried out using the Mesocite module embedded in the Materials Studio 6.0 package from Accelrys, Inc.³⁷ In this paper, all the simulations were accomplished in a cubic box with a size of 80 × 80 × 80 R_c³ with periodic boundary conditions. All particles of NPs located at the center of the fixed region were constrained on its motion, by fixing positions. The enclosed cells were composed of 5%, 10% and 15% concentrations Pluronic copolymers in aqueous solutions and the polymer concentration was described by the number ratio of polymer beads to total beads. The temperature in all simulations was T = 298 K. The molecular conformations of Pluronic copolymers were geometrically optimized by CG force field for the calculations: the PEO were around and close to NPs, the PPO freely stretched in aqueous solutions.³⁸ NPT ensemble was not used in this system because the NPs beads were fixed. After geometrically optimized, a run of 10 ns under NVT ensemble conditions was performed. In the NVT equilibration, temperature was controlled by a Berendsen thermostat with a time step of τ = 2 fs, and the trajectories were recorded every 1 ps.^35,39 A twin-range cutoff of 12.5 Å was employed, and the long-range dispersion corrections were also implemented for both energy and temperature.⁴⁰

3. Results and discussion

3.1 Self-assembled film structure

3.1.1 Self-assembled film morphologies. CGMD firstly simulated the system of Pluronic F127 copolymers in aqueous solutions to calculate the radius of gyration and diffusion coefficient of Pluronic F127 copolymers. As simulated results shown, the diffusion coefficient of F127 copolymers in aqueous solutions is 2.92 × 10⁻¹⁰ m² s⁻¹ which is similar to that found experimental data 3.00 × 10⁻¹⁰ m² s⁻¹.⁴¹ The radius of gyration of Pluronic F127 copolymers in aqueous solutions is 1.68 nm, it is also well agree with experimental data 1.7 nm.⁴² Then, the self-assembled films of triblock copolymer on different hydrophobicity of nanoparticle surfaces with different concentrations of Pluronic copolymers were carried out by CGMD. The simulated results for the systems which were composed of Pluronic F127 copolymers at concentrations of 5%, 10% and 15%, respectively, were shown in Fig. 2. It has been found that both the hydrophobicity of NPs and the concentration of Pluronic F127 played a role in the morphology of self-assembled films. The Fig. 2 indicated a drastic difference in the self-assembled film morphologies was encountered with increase in Pluronic concentration. At lower concentration (like 5%) a completely covered film was formed by the attachment of crimp polymer chain structure on the NP surfaces, which gives rise to a special film with a shell-layered structure. With further rise in concentration of F127 (like 10% and 15%), the shell-layered structure almost disappears and eventually star-shaped films were formed. It is evident that the inner part of the films is made of hydrophobic PPO attached to the NPs surfaces while the hydrophilic PEO blocks are directed toward aqueous. Some similar experimental results have been reported by Liu et al.¹⁴ As the atomic force microscopy results shown, there are some protruding parts in adsorbed layer with increasing the concentrations of Pluronic polymers and the thickness of adsorbed layer also become larger. These experimental results can be explained by the conformational transition from simulation results. Compared with different hydrophobicity of nanoparticle surfaces, it can be found that the SS hydrophobic model tended to be shell-layered structure films on NP surfaces. Nevertheless, the Fig. 2 also depicted concentrations of F127 had a significant influence on film structure transition from shell-layered to star-shaped structure.

Fig. 2 The representative simulation snapshots obtained for different concentrations of F127 assembled at different hydrophobicity of nanoparticle surfaces. The degrees of hydrophobic are (a–c) super attractive–super repulsive (SS model), (d–f) attractive–repulsive (AR model), (g–i) almost attractive–almost repulsive (AA model) and (j–l) intermediate–almost intermediate (IA model). More details hydrophobic properties of NP can be found in ESI.† From left to right for each row, different concentrations are for degrees of hydrophobic NP: 5%, 10%, 15%, respectively.

3.1.2 Density distribution and mean self-assembled film thickness. The density distribution could be obtained according to the snapshot of the simulation, and density distributions for different systems were shown in Fig. 3 and S1 of ESI.† The average numbers of EO, PO and F127 beads per volume unit were plotted across the box X direction. According to the density profiles, the interfacial thickness was calculated by the “90–10” criterion, which was defined as the distance along the interface over which the densities of NPs surfaces from 90% to 10% of their bulk values.^43,44 Interfacial thickness was an important interfacial physical property that provided a quantitative measure for the size of the interface or self-assembled film. In this paper, we defined two types of interfacial thickness R_in and R_out, as shown in Fig. 4a. In order to consider the contribution of PEO blocks, R_in was calculated by the sum of PEO blocks effective density value (the distance along the interface over which the densities of NPs surfaces from 90% to 75% of their bulk values) and PPO blocks effective density value (the distance along the interface over which the densities of NPs surfaces from 90% to 10% of their bulk values). The R_out was defined by the F127 densities of NPs surfaces from 90% to 10% of their bulk values. The calculated interfacial thicknesses of R_in and R_out were given in Fig. 4b and c.

Fig. 3 Density distribution of F127 (black), PO block (red) and EO block (blue) absorbed on NP surfaces for SS (super attractive–super repulsive) hydrophobic degree. In this case, (a) 5%, (b) 10%, (c) 15% concentration, respectively. The other density distributions for different hydrophobic nanoparticle surfaces were given in Fig. S1 of ESI.†

Fig. 4 (a) Schematic of R_in and R_out, (b) R_in as a function of concentrations and (c) R_out as a function of concentrations.

As we can see from Fig. 3, the density profiles for the PEO blocks of F127 on the hydrophobic surfaces model obviously were lower than PPO blocks with the different concentrations of F127 increase. At 5% concentrations, the density profiles of PEO blocks is relatively concentrated (from 22–56 at X direction), while the wider distribution (from 10–75 at X direction) for density profiles of PEO blocks is found. There were similar results about other hydrophobic surface models' density profiles, as can be seen from Fig. S1 of ESI.† These changes of density profiles also exhibited that the increase of R_out while decrease of R_in with the concentrations of F127 increase, as shown in Fig. 4b and c. At lower concentration (like 5%), a self-assembly behavior of highly coiled state of the copolymer occurred on hydrophobic nanoparticle surface. At higher concentration (like 10% and 15%), the density profiles indicated the F127 molecules were located mainly at the NPs/water interface with the PEO blocks in water phase and PPO blocks adsorbed on NPs surfaces (confirmed by Fig. 2). For the different hydrophobicity of NPs surfaces, the R_out always grow higher while R_in become lower with the increase of concentrations which demonstrated the concentration mediates the self-assembled film structure transition.

3.2 Self-assembled film properties

3.2.1 Radial distribution function (RDF). To further characterize the self-assembly behavior of F127 on NPs surfaces, the radial distribution function was introduced in this paper. The radial distribution function was computed for all pairs of beads or centroids in the set which were closer than the cutoff value. Radial distribution function could be calculated using following equation^45,46where {ΔN_ij(r → r + Δr)} was the ensemble averaged number of j around i within a shell from r to r + Δr, V was the system volume, N_i and N_j were number of i and j, respectively.

For the SS hydrophobic surfaces model, a sharp peak was observed at approximately 0.5 nm in the g(r) for PO–NPs, as shown in Fig. 5. This implied a strong adsorbed interaction between the PPO blocks and NPs surfaces. Though the g(r) for EO–NPs also exhibited a peak at 0.75 nm, the peak was lower indicating a weaker adsorbed interaction. Thus, the g(r) for F127–NPs existed two small peaks at 0.5 nm and 0.75 nm which reflected the interaction of PO–NPs and EO–NPs. Obviously, the adsorbed interaction between the PPO blocks and NPs surfaces were strongest because of NPs' hydrophobic nature. The g(r) for EO–PO was also given in Fig. 5, and there was a peak at 0.48 nm which agreed with the reported result data.⁴⁷ There were similar results for other different hydrophobicity of surfaces which were given in Fig. S2 of ESI.†

Fig. 5 The radial distribution functions g(r) for different concentrations of F127 considered in this work. In this case, (a) 5%, (b) 10% and (c) 15% with super attractive–super repulsive (SS model) hydrophobic nanoparticle surfaces. The other g(r)s for different hydrophobic nanoparticle surfaces were given in Fig. S2 of ESI.†

3.2.2 Order parameter. In dynamic simulation processes, an order parameter could be monitored to indicate the changes occurring in the molecular structures, and could thus yielded characteristics of the phase separation and compressibility. The order parameter (P), which was the mean squared deviation from homogeneity for a particular species (A) in volume V, was defined as:⁴⁸

P_A = 〈(η_A − η⁰_A)²〉 (2)

where η⁰_A was the overall volume fraction of species A, and η_A was the local volume fraction of species A; note that both quantities were dimensionless in CGMD. Therefore, small values for P_A indicated a homogeneous system, and large values suggested strong phase separation.

The order parameters P_A of Pluronic copolymers calculated from eqn (2) as a function of the simulation time at different concentrations were given in Fig. 6. The increasing order parameter P_A of Pluronic copolymers self-assembled on NPs surfaces with time indicated the phase separation got stronger and the morphology structures of Pluronic copolymers on NPs hydrophobic surfaces were more regularly. Moreover, the PPO blocks of F127 always earlier reached the balance values compared with PEO blocks because of NPs' hydrophobic interactions. Though different hydrophobicity of NP surfaces were simulated, the order parameter P_A grew higher with the increase of F127 concentrations. When the concentration of F127 was 5%, the order parameter P_A of PEO blocks were higher than PPO blocks, likely due to the longer Gaussian chain. In short, the order parameter P_A well reflected the self-assembled film morphologies (see Fig. 2).

Fig. 6 Order parameter versus simulation the time for F127 assembled at (a) 5%, (b) 10% and (c) 15% concentration, respectively. For each small figure, they are for different hydrophobicity of NP surfaces of super attractive–super repulsive (SS model), attractive–repulsive (AR model), almost attractive–almost repulsive (AA model) and intermediate–almost intermediate (IA model), respectively.

3.3 Structural transition mechanism

3.3.1 Free energy. The free energy profiles for different concentrations of F127 were presented in Fig. 7. At the same concentrations of F127, it was evident from the Fig. 7 that the system free energies change: SS model > AR model > AA model > IA model. These free energy changes had a positive correlation with hydrophobic degrees of NPs surfaces. As we known, the lower free energy of the system was the stronger adsorbed interactions between Pluronic copolymers and NPs surfaces. Owing to strong affinity between hydrophobic surface and PPO hydrophobic block of F127, the aggregated and extended polymer chains tried to cover up the underlying hydrophobic nanoparticle surfaces. At low concentrations (like 5%), the PEO blocks would participate in initial coating though there were weak adsorbed interactions between PEO blocks and NPs surfaces. This was expected, since the surface became increasingly unavailable for adsorption with concentrations (or named feeding phenomenon).⁴⁹ Actually, there existed a weak interaction between PEO blocks and NPs surfaces.^13,31 Thus, at low concentrations, the lower free energy of the system (see Fig. 2a and j) would result into the formation of shell-layered structure films. However, at high concentration (like 10%, 15%), the surface became increasingly unavailable giving rise to strong self-assembly between PPO blocks and NPs surfaces rather weak self-assembly between PEO blocks and NPs surfaces. Consequently, the PEO blocks of Pluronic copolymers stretched into aqueous phase. From Fig. 7, we also could find the free energy of system decreased with the increase concentrations of Pluronic F127 copolymers when on the same hydrophobic degree NPs surface. Increasing concentration of Pluronic F127 copolymers resulted more possibility of PPO assembly on limited NPs surfaces owing to the strong interactions between PPO and NPs surfaces, thus resulted into lower free energy with increasing the concentrations of triblock copolymers. Moreover, the concentrations of Pluronic have a greater impact on decreasing free energy of system than the hydrophobicity of NPs. These also revealed that the Pluronic concentration majorly induced the transition of self-assembled films rather than the hydrophobicity of NPs.

Fig. 7 Free energy versus simulation the time for F127 assembled at (a) 5%, (b) 10% and (c) 15% concentration, respectively.

3.3.2 Radius of gyration (R_g). To gain more insight about the molecular configuration of Pluronic copolymers on hydrophobic surfaces, the radius of gyration R_g was introduced to illustrate the conformational changes of Pluronic copolymers. The radius of gyration R_g showed the degree of stretching. It could be calculated using the following equation:⁵⁰where r⃑_i denoted the vector the whole copolymers molecules.

The calculated radius of gyration R_g distributions for different degree of hydrophobic nanoparticle surfaces were given in Fig. 8. Though different hydrophobicity of nanoparticle surfaces were simulated, the radius of gyration R_g of Pluronic copolymers on hydrophobic surfaces distributed at bigger values with the increase in concentrations. At the concentrations of 5%, the radius of gyration R_g of Pluronic copolymers on hydrophobic surfaces distributed from 0.8 nm to 1.2 nm, while the distribution of radius of gyration R_g would change from 1.0 nm to 1.7 nm when the concentration was 10%. At the concentrations of 15%, the radius of gyration R_g reached to the extreme value (from 1.3 nm to 2.4 nm), and the Pluronic copolymers showed freely stretching conformation (see Fig. 2). In addition, increasing of concentrations of Pluronic copolymers led to larger radius of gyration R_g with the formation of star-shaped film on NPs surfaces. Interestingly, the PPO blocks of F127 covering on NPs surfaces displayed special assembled pattern: transform from word “S-shaped” to word “U-shaped” or “W-shaped” with the increase in concentrations. As the free energy shown, this transform also indicated the changes of interaction between Pluronic copolymers and NPs surfaces.

Fig. 8 The radius of gyration R_g distributions for different degree of hydrophobic nanoparticle surfaces. In this case, (a) super attractive–super repulsive(SS model), (b) attractive–repulsive (AR model), (c) almost attractive–almost repulsive (AA model) and (d) intermediate–almost intermediate (IA model), respectively.

4. Conclusions

We have performed coarse-grained molecular dynamic (CGMD) simulations to investigate the structural transition of PEO–PPO–PEO triblock copolymers self-assembled films with different polymer concentrations on different hydrophobicity of nanoparticle (NP) surfaces. At lower concentration (like 5%) an completely covered film was formed by the attachment of crimp polymer chain layered-like structure on a fully covered film. Correspondingly, a film with a shell-layered structure was formed from the coverage or thickness point of view. With further rise in concentration, the shell-layered structure almost disappeared and eventually star-shaped films were formed. These films, consisted with two bilayers of triblock polymer, comprised variable stretching conformation and phase separation through alternating stacking. The radius of gyration R_g revealed that the PEO blocks of Pluronic copolymers gradually stretched into aqueous phase with increase the concentrations of Pluronic copolymers. Moreover, PPO blocks of Pluronic copolymers covering on NPs surfaces displayed special assembled pattern: transform from “S-shaped” to word “U-shaped” or “W-shaped” with the increase in concentrations. The simulation results also demonstrated that it was that the feeding phenomenon and adsorbed interactions led to this structural transition by mediating concentration.

Acknowledgements

This work is supported by the scientific research fund of Sichuan Provincial Education Department (13ZB0100, 15ZA0317 and 15ZA0363), and Dazhou Administration of Science & Technology (KJJ201403). We are grateful to Prof. Shuangliang Zhao, in Research Group of Interface Science and Thermodynamics of East China University of Science and Technology (ECUST) for use of Material Studio.

References

1. G. K. Xu, Y. Li, B. Li, X. Q. Feng and H. Gao, Self-assembled lipid nanostructures encapsulating nanoparticles in aqueous solution, Soft Matter, 2009, 5(20), 3977–3983.
2. J. B. Haun and D. A. Hammer, Quantifying nanoparticle adhesion mediated by specific molecular interactions, Langmuir, 2008, 24, 8821–8832.
3. Y. Li, O. J. Rojas and J. P. Hinestroza, Boundary Lubrication of PEO–PPO–PEO Triblock Copolymer Physisorbed on Polypropylene, Polyethylene, and Cellulose Surfaces, Ind. Eng. Chem. Res., 2012, 51, 2935–2944.
4. A. van Blaaderen, Materials science: colloids get complex, Nature, 2006, 439, 545–546.
5. D. Zerrouki, J. Baudry, D. Pine, P. Chaikin and J. Bibette, Chiral colloidal clusters, Nature, 2008, 455, 380–382.
6. A. S. Robbes, J. Jestin and F. Meneau, et al., Homogeneous dispersion of magnetic nanoparticles aggregates in a ps nanocomposite: Highly reproducible hierarchical structure tuned by the nanoparticles' size, Macromolecules, 2010, 43, 5785–5796.
7. R. M. Erb, H. S. Son, B. Samanta, V. M. Rotello and B. B. Yellen, Magnetic assembly of colloidal superstructures with multipole symmetry, Nature, 2009, 457, 999–1002.
8. S. Maskey, J. M. D. Lane, D. Perahia and G. S. Grest, Structure of rigid polymers confined to nanoparticles: molecular dynamics simulations insight, Langmuir, 2016, 32, 2102–2109.
9. A. Sambasivam, A. Sangwai and R. Sureshkumar, Self-assembly of nanoparticle–surfactant complexes with rodlike micelles: a molecular dynamics study, Langmuir, 2016, 32, 1214–1219.
10. D. E. Koshland, The lock-key theory and the induced fit theory, Angew. Chem., Int. Ed. Engl., 1995, 33, 2375–2378.
11. F. Tiberg, M. Malmsten, P. Linse and B. Lindman, Kinetic and equilibrium aspects of block copolymer adsorption, Langmuir, 1991, 7, 2723–2730.
12. F. Alvarez, E. A. Flores, L. V. Castro, J. G. Hernandez, A. Lopez and F. Vazquez, Dissipative particle dynamics (DPD) study of crude oil–water emulsions in the presence of a functionalized co-polymer, Energy Fuels, 2010, 25, 562–567.
13. P. Brandani and P. Stroeve, Adsorption and desorption of PEO–PPO–PEO triblock copolymers on a self-assembled hydrophobic surface, Macromolecules, 2003, 36, 9492–9501.
14. X. Liu, D. Wu, S. Turgman-Cohen, J. Genzer, T. W. Theyson and O. J. Rojas, Adsorption of a nonionic symmetric triblock copolymer on surfaces with different hydrophobicity, Langmuir, 2010, 26, 9565–9574.
15. T. Sakai and P. Alexandridis, Mechanism of gold metal ion reduction, nanoparticle growth and size control in aqueous amphiphilic block copolymer solutions at ambient conditions, J. Phys. Chem. B, 2005, 109, 7766–7777.
16. S. Zhou, A. Sugawara-Narutaki, S. Tsuboike, J. Wang, A. Shimojima and T. Okubo, Nanoparticle Vesicles with Controllable Surface Topographies through Block Copolymer-Mediated Self-Assembly of Silica Nanospheres, Langmuir, 2015, 31, 13214–13220.
17. S. K. Agrawal, N. Sanabria–DeLong, G. N. Tew and S. R. Bhatia, Nanoparticle-reinforced associative network hydrogels, Langmuir, 2008, 24, 13148–13154.
18. Y. Lin, V. K. Daga, E. R. Anderson, S. P. Gido and J. J. Watkins, Nanoparticle-driven assembly of block copolymers: a simple route to ordered hybrid materials, J. Am. Chem. Soc., 2011, 133, 6513–6516.
19. S. Chen, Y. Li and C. Guo, et al., Temperature-responsive magnetite/PEO–PPO–PEO block copolymer nanoparticles for controlled drug targeting delivery, Langmuir, 2007, 23, 12669–12676.
20. K. Shi, C. Lian, Z. Bai, S. Zhao and H. Liu, Dissipative particle dynamics study of the water/benzene/caprolactam system in the absence or presence of non-ionic surfactants, Chem. Eng. Sci., 2015, 122, 185–196.
21. K. Hagita, H. Morita, M. Doi and H. Takano, Coarse-Grained Molecular Dynamics Simulation of Filled Polymer Nanocomposites under Uniaxial Elongation, Macromolecules, 2016, 49, 1972–1983.
22. Q. Wang, D. J. Keffer, D. M. Nicholson and J. B. Thomas, Coarse-grained molecular dynamics simulation of polyethylene terephthalate (PET), Macromolecules, 2010, 43, 10722–10734.
23. V. Ganesan and A. Jayaraman, Theory and simulation studies of effective interactions, phase behavior and morphology in polymer nanocomposites, Soft Matter, 2014, 10, 13–38.
24. S. Nawaz and P. Carbone, Coarse-Graining Poly(ethylene oxide)–Poly(propylene oxide)–Poly(ethylene oxide) (PEO–PPO–PEO) Block Copolymers Using the MARTINI Force Field, J. Phys. Chem. B, 2014, 118, 1648–1659.
25. L. Monticelli, S. K. Kandasamy, X. Periole, R. G. Larson, D. P. Tieleman and S. J. Marrink, The MARTINI Coarse-Grained Force Field: Extension to Proteins, J. Chem. Theory Comput., 2008, 4, 819–834.
26. J. J. Uusitalo, H. I. Ingólfsson, P. Akhshi, D. P. Tieleman and S. J. Marrink, Martini coarse-grained force field: extension to DNA, J. Chem. Theory Comput., 2015, 11, 3932–3945.
27. G. Rossi, I. G. Elliott, T. Ala-Nissila and R. Faller, Molecular dynamics study of a MARTINI coarse-grained polystyrene brush in good solvent: structure and dynamics, Macromolecules, 2011, 45, 563–571.
28. P. A. Oroskar, C. J. Jameson and S. Murad, Surface-functionalized nanoparticle permeation triggers lipid displacement and water and ion leakage, Langmuir, 2015, 31, 1074–1085.
29. R. Wu, M. Deng, B. Kong and X. Yang, Coarse-grained molecular dynamics simulation of ammonium surfactant self-assemblies: micelles and vesicles, J. Phys. Chem. B, 2009, 113, 15010–15016.
30. S. Hezaveh, S. Samanta, A. De Nicola, G. Milano and D. Roccatano, Understanding the interaction of block copolymers with DMPC lipid bilayer using coarse-grained molecular dynamics simulations, J. Phys. Chem. B, 2012, 116, 14333–14345.
31. S. Hezaveh, Study the Interaction Mechanisms of Block Copolymers with Biological Interfaces, Doctoral dissertation, University of Salerno, Italy, 2012.
32. H. Shi, S. Zhang, R. Steitz, J. Chen, S. Uredat and G. H. Findenegg, Surface coatings of PEO–PPO–PEO block copolymers on native and polystyrene-coated silicon wafers, Colloids Surf., A, 2004, 246(1), 81–89.
33. G. Srinivas, R. V. Mohan and A. D. Kelkar, Polymer micelle assisted transport and delivery of model hydrophilic components inside a biological lipid vesicle: a coarse-grain simulation study, J. Phys. Chem. B, 2013, 117, 12095–12104.
34. S. J. Lee, P. H. Schlesinger, S. A. Wickline, G. M. Lanza and N. A. Baker, Simulation of fusion-mediated nanoemulsion interactions with model lipid bilayers, Soft Matter, 2012, 8, 7024–7035.
35. R. Wu, M. Deng, B. Kong and X. Yang, Coarse-grained molecular dynamics simulation of ammonium surfactant self-assemblies: micelles and vesicles, J. Phys. Chem. B, 2009, 113, 15010–15016.
36. http://wiki.roblox.com/index.php?title=Polar_coordinate_system.
37. Accelrys MS Modeling 6.0., Accelrys, Inc., San Diego, 2011.
38. Y. Ruiz-Morales and O. C. Mullins, Coarse-grained molecular simulations to investigate asphaltenes at the oil–water interface, Energy Fuels, 2015, 29, 1597–1609.
39. M. Vögele, C. Holm and J. Smiatek, Properties of the polarizable MARTINI water model: A comparative study for aqueous electrolyte solutions, J. Mol. Liq., 2015, 212, 103–110.
40. C. Arnarez, J. J. Uusitalo and M. F. Masman, et al., Dry Martini, a coarse-grained force field for lipid membrane simulations with Implicit solvent, J. Chem. Theory Comput., 2014, 11, 260–275.
41. P. Alexandridis and T. A. Hatton, Poly(ethylene oxide)–poly(propylene oxide)–poly(ethylene oxide) block copolymer surfactants in aqueous solutions and at interfaces: thermodynamics, structure, dynamics, and modeling, Colloids Surf., A, 1995, 96(1), 1–46.
42. P. Brandani and P. Stroeve, Kinetics of adsorption and desorption of PEO–PPO–PEO triblock copolymers on a self-assembled hydrophobic surface, Macromolecules, 2003, 36, 9502–9509.
43. Y. Li, Y. Guo, M. Bao and X. Gao, Investigation of interfacial and structural properties of CTAB at the oil/water interface using dissipative particle dynamics simulations, J. Colloid Interface Sci., 2011, 361, 573–580.
44. M. Luo and L. L. Dai, Molecular dynamics simulations of surfactant and nanoparticle self-assembly at liquid–liquid interfaces, J. Phys.: Condens. Matter, 2007, 19, 375109.
45. Z. Luo and J. Jiang, pH-Sensitive drug loading/releasing in amphiphilic copolymer PAE–PEG: integrating molecular dynamics and dissipative particle dynamics simulations, J. Controlled Release, 2012, 162, 185–193.
46. X. Song, P. Shi, M. Duan, S. Fang and Y. Ma, Investigation of demulsification efficiency in water-in-crude oil emulsions using dissipative particle dynamics, RSC Adv., 2015, 5, 62971–62981.
47. D. Bedrov, C. Ayyagari and G. D. Smith, Multiscale modeling of poly(ethylene oxide)–poly(propylene oxide)–poly(ethylene oxide) triblock copolymer micelles in aqueous solution, J. Chem. Theory Comput., 2006, 2, 598–606.
48. H. Liu, Y. Li, W. E. Krause, M. A. Pasquinelli and O. J. Rojas, Mesoscopic Simulations of the Phase Behavior of Aqueous EO₁₉PO₂₉EO₁₉ Solutions Confined and Sheared by Hydrophobic and Hydrophilic Surfaces, ACS Appl. Mater. Interfaces, 2011, 4, 87–95.
49. G. Srinivas, S. O. Nielsen, P. B. Moore and M. L. Klein, Molecular dynamics simulations of surfactant self-organization at a solid–liquid interface, J. Am. Chem. Soc., 2006, 128, 848–853.
50. P. Nikunen, I. Vattulainen and M. Karttunen, Reputational dynamics in dissipative particle dynamics simulations of polymer melts, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 036713.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra18739k

‡ Present address: School of Chemistry and Chemical Engineering, Southwest Petroleum University, Chengdu, Sichuan 610500, China.

---