Multi-response optimization followed by multivariate calibration for simultaneous determination of carcinogenic polycyclic aromatic hydrocarbons in environmental samples using gold nanoparticles

Abstract

In this study, a multivariate-based strategy was developed for simultaneous determination of thirteen carcinogenic polycyclic aromatic hydrocarbons (PAHs) in water samples using gold nanoparticles (AuNPs) as solid-phase extraction (SPE) sorbent combined with gas chromatography (GC). The extraction technique is based on the strong affinity between citrate-capped AuNPs and PAHs. Furthermore, characterization of AuNPs was performed by UV-vis spectroscopy and transmission electron microscopy (TEM) techniques. A rotatable central composite design (CCD) combined with multiple linear regression (MLR) was used for designing the extraction procedure and developing models using the GC peak areas of 13 PAHs. Moreover, multi-response optimization using the Derringer desirability function was utilized to find optimum conditions, which were 7.22 min adsorption vortex time, 5 μL of 1,3-propanedithiol as desorption solvent, 44 μL methanol, 15 μL n-nonane as acceptor solvent and 9.63 min desorption vortex time. The optimized method was then used for identification and quantification of target PAHs in standard and spiked samples using partial least squares regression (PLSR). Different variable selection methods including PLS regression vector (RV), variable importance in projection (VIP) and selectivity ratio (SR) were tested and RV showed the best performance. Finally, the proposed strategy was successfully tested for the analysis of spiked water samples (i.e., from tap, well and farm).

---

1. Introduction

Due to the increase of wastewater discharge to the environment, contamination by organic pollutants in water has been rising over the past decades. Polycyclic aromatic hydrocarbons (PAHs) are a large class of well-known carcinogenic organic pollutants, which are mainly formed by pyrolytic processes and particularly due to the incomplete combustion of organic matter.¹ Therefore, human exposure to PAHs as carcinogenic compounds cannot be avoided.² The US Environmental Protection Agency (US-EPA) includes sixteen PAHs in its priority pollutants list.³ It is important to note that PAHs are present in environmental samples at ppb levels or lower due to their large hydrophobicity.¹ Owing to the complexity of the sample matrices, the low concentrations of PAHs, their solubility in water and similarity in their properties, development of potent analytical methods, including a sample preparation technique followed by a separation technique, is mandatory.⁴ To extract the sought analytes from aqueous samples, numerous adsorption and absorption materials have been used in different sample preparation methods, such as solid-phase extraction (SPE)⁵ and solid-phase microextraction (SPME).^6,7 Nowadays, nanotechnology can be considered as a milestone in materials science. Nanomaterials-based sample preparation techniques play important roles in many analytical procedures for extraction and enrichment of analytes. Metallic nanoparticles (MNPs), metal–organic frameworks (MOFs), carbon nanomaterials, and siliceous nanoparticles are the most frequently used nanomaterials for sample preparation and separation.^8,9 Gold nanoparticles (AuNPs) are reliable and frequently used nanomaterials in chemistry due to their high surface-to-volume ratio, long-term stability, easy synthesis and compatibility with a large class of organic compounds.^10,11 Using AuNPs without any modification for the extraction of PAHs from water samples, which is a modified version of SPE (solid phase nanoextraction, SPNE), has been proposed by Wang and Campiglia.¹² This extraction technique takes advantage of the strong physicochemical affinity between AuNPs and PAHs.¹² In addition, this technique presents several features that meet the concept of green analytical chemistry. The small volume of organic solvents and extracting solution makes SPNE a cost-effective method with low solvent consumption.¹³

Among different analytical techniques, gas chromatography (GC) and high-performance liquid chromatography (HPLC) are best options for the analysis of PAHs in various sample matrices.^14–16 On the other hand, the optimization of extraction and analysis procedures are usually based on a univariate approach. In this regard, the interpretation of the obtained results is facilitated, but interactions between variables are not taken into account which causes a false minimum or maximum. Multivariate optimization techniques (e.g., factorial designs (FD) and response surface methodology (RSM)) have been applied to optimize the extraction procedures.^17–20

It is important to note that extraction methods are not usually selective even under optimized conditions; therefore, a number of interfering compounds will be extracted.^21,22 Multivariate chemometric methods (i.e., multivariate calibration) have been proposed in the past decades to compensate for the lack of selectivity in chromatography and to obtain pure qualitative and quantitative chromatographic information of the target components. Among different multivariate calibration methods, partial least squares regression (PLSR) has attracted great attention in chemistry in recent years due to its unique properties and the wide variety of its application.^23,24 PLSR has been frequently used in the chromatographic analysis of organic pollutants in complex biological and environmental samples.²⁵

To the best of our knowledge, there is no report in literature regarding the multivariate view on determination of PAHs using AuNPs. As SPNE is a new extraction technique, this multivariate view can therefore extend its applicability domain. Thus, in our study, first, the SPNE procedure was tested by different types of both acceptor and desorption solvents to achieve more satisfactory and efficient extraction results. Secondly, multivariate optimization of other parameters, which influence the extraction procedure, was accomplished using a multi-response approach, which considers the individual GC peak areas of 13 PAHs. Therefore, more reliable extraction parameters were obtained, which led to better analytical performance of SPNE for determination of PAHs. In addition, multivariate calibration using PLSR somehow compensated for the lack of selectivity of the extraction and analysis method by decomposing the mixed data matrix into the contribution of pure components. Therefore, more reliable analytical figures of merit could be obtained. In PLS modeling, GC profiles of standard mixtures of 13 PAHs were considered for modeling and different variable selection methods, such as regression vector (RV), variable importance in projection (VIP) and selectivity ratio (SR),^23,24 were tested on the performance of the calibration model. Considering all of these method improvements, an efficient, simple, and robust method has been exploited for the determination of PAHs in this contribution. It is concluded that this developed multivariate-based strategy significantly improved the performance of AuNPs to extract PAHs from aqueous samples.

2. Experimental

2.1. Chemicals

A standard mixture of 13 PAHs (EPA-525-PAH-Mix-A) containing a mixture of acenaphthylene (Aceny), anthracene (Ant), benz[a]anthracene (B[a]A), benzo[b]fluoranthene (B[b]F), benzo[k]fluoranthene (B[k]F), benzo[ghi]perylene (B[ghi]P), benzo[a]pyrene (B[a]P), chrysene (Chr), dibenzo[a,h]anthracene (DB[a,h]A), fluorene (Flu), indeno[1,2,3-cd]pyrene (I[1,2,3-cd]P), phenanthrene (Phen), and pyrene (Pyr) in methylene chloride, with the concentration of each single compound being 500 μg mL⁻¹, was provided from Sigma-Aldrich (MO, USA). A stock standard solution (50 μg mL⁻¹) of PAHs was prepared by appropriate dilution of the original standard in methanol and was stored at 4 °C. Working solutions of PAHs were prepared by dilution of stock solutions with methanol.

Chloroauric acid (HAuCl₄·3H₂O), trisodium citrate and methanol were purchased from Merck (Darmstadt, Germany). Analytical grade toluene-3,4-dithiol, 1-ethanethiol, 1,2-ethanedithiol, 1,3-propanedithiol, n-octane, n-nonane and n-decane were purchased from Sigma-Aldrich (MO, USA) and Merck (Darmstadt, Germany).

Real water samples from tap, well and farm water were collected from the cold-water tap of our department, a well in the north of Tehran and a farm in the north of Iran, respectively. The water samples were filtered through a 0.45 μm PTFE membrane and then stored in dark glass bottles at 4 °C.

2.2. AuNPs synthesis

The AuNPs, in this study, were prepared by reducing HAuCl₄ with trisodium citrate by Fren's method.²⁶ Briefly, an aliquot of 50 mL aqueous solution of HAuCl₄ (0.25 mM) was heated to boil and then 876 μL of trisodium citrate (1%) was added to it. In about 25 s, the boiling solution turns faintly blue. After ∼70 s, the blue color changed to deep red. The solution was set aside to cool to room temperature. Synthesized AuNPs were kept inside the aqueous solution, where they were synthesized in dark at 4 °C. In Fren's method, it is common to obtain spherical AuNPs with different diameters by varying the citrate/Au³⁺ molar ratio. AuNPs with diameter 20 nm can be prepared from a citrate/Au³⁺ molar ratio of 4.2. The prepared AuNPs were purified using a membrane filter with 0.2 μm pore size to remove large particles. The physical integrity of AuNPs was monitored periodically using UV-vis spectroscopy. AuNPs exhibited a characteristic surface plasmon resonance (SPR) wavelength at 526 nm. Furthermore, transmission electron microscopy (TEM) was used to estimate the size and distribution of AuNPs. TEM images exhibited the formation of monodispersed NPs with a mean diameter of 20 nm.

2.3. Extraction procedure using AuNPs

For the SPNE procedure, a 1 mL aliquot of the water sample was mixed with 1 mL of 20 nm AuNPs with an estimated concentration of 12 nM (according to ref. 27) and then stirred for 20 min to make the solution homogenous. The mixture was vigorously shaken for 7.13 min and centrifuged for 20 min at 12 000 rpm. The supernatant was separated from the precipitate with a micro-pipette. 5 μL of desorption solvent (1,3-propanedithiol), 44 μL of methanol, and 15 μL of acceptor solvent (n-nonane) were added to the precipitate. The new mixture was shaken for 9.38 min and centrifuged for 10 min at 12 000 rpm. It should be pointed out that fluorescence spectroscopy was used for evaluation of adsorption and desorption steps. Finally, the n-nonane phase was separated and 2 μL was injected into the GC-FID. The extraction and GC-FID analysis were repeated three times to control random variations in the system.

External calibration samples were prepared in methanol at seven concentration levels within the range of 0.10–70.00 ng mL⁻¹ for 13 PAHs and were extracted using SPNE in optimum conditions. Real water samples (from tap, well and farm) as test calibration samples were spiked at three different concentration levels of 2, 5 and 20 ng mL⁻¹ with the standard mixture of PAHs and stored in dark at 4 °C prior to analysis.

2.4. Chemometric analysis

Based on preliminary studies, five effective factors on SPNE including type and volume of desorption and acceptor solvents, methanol volume and vortex times were designed using rotatable circumscribed central composite design (CCD) with α = 2.0. In this regard, the individual peak areas of 13 EPA-PAHs calculated by the ChemStation software of the GC-FID were considered as responses for model development and optimization steps. It should be pointed out that the PAHs mixture of 50 ng mL⁻¹ was used for optimization. A total of 36 experiments were designed and were performed in two orthogonal blocks in order to remove the unexpected variation caused by some changes during the course of the experiment. It is important to note that the factorial part of CCD was half-fraction (2_V⁵⁻¹) with resolution V. Multiple linear regression in backward mode (backward-MLR) and analysis of variance (ANOVA) methods were used to select a suitable response surface model, the significance of the model equation, and the model terms. In modeling, the terms with p-value less than 0.05 were regarded as significant and they were kept in the model. However, in some cases, terms with 0.05 < p < 0.1 affect the goodness of fit in the model. Therefore, a confidence band between 90–95% was considered to keep the most significant terms appearing in this confidence band in the model. On the other hand, the terms with p-value greater than 0.10 were regarded as not significant and these factors were removed from the model. Therefore, 13 different models were developed for 13 PAHs and their validity was confirmed using different statistical parameters. For simultaneous optimization of 13 developed models and to obtain the global optimum values of the effective parameters on the SPNE procedure, Derringer's desirability function (D) was used.²⁸ The D is a global function that varies from 0 (totally undesirable) to 1 (all responses are totally desirable simultaneously) and can be defined using the following equation:

D = (d₁^r₁ × d₂^r₂ ×…× d_m^r_m)^1/∑r_j (1)

where d₁,…, d_m correspond to the individual desirability function for each response, m is the number of considered responses (13 in this study) and r is the relative importance of each response over the other responses (1 in this study). The same importance was given to all responses and the optimum values corresponding to the maximum global desirability function were obtained. The main objective of the optimization was the determination of optimum values of effective extraction factors from the obtained model using experimental data. Optimization was carried out using a downhill simplex (Nelder–Mead) optimization method. After obtaining the optimum SPNE parameters, the extraction procedure and chromatographic analysis were repeated three times (n = 3) at optimum conditions and the obtained responses for developed models were compared with the experimental ones.

After optimizing the extraction procedure, a new set of PAH samples were prepared in seven concentration levels (and in triplicate) in the range 0.1–70 ng mL⁻¹ (21 samples as the calibration set), analyzed in optimum extraction conditions and their GC-FID profiles were recorded. In this regard, the two different strategies of univariate and multivariate calibration were performed.

For univariate calibration, as the conventional way of calibration, the peak area of the target PAHs was considered as the response and ordinary least-squares (OLS) was used to build calibration curves, to calculate analytical figures of merit and to predict concentration of PAHs in spiked water samples. However, due to the similar molecular structures of PAHs and their strong chromatographic overlap, baseline, and presence of impurity peaks, which can overlap with the target peak, calculation of the peak area of the individuals is difficult and causes systematic error in calibration. Therefore, all analytical figures of merit can be affected. Due to the abovementioned challenges in the case of univariate calibration, multivariate calibration has been recommended.

For multivariate calibration, PLSR modeling (i.e., SIMPLS algorithm²⁴) was performed for calibration data. The GC profile for each sample had 555 time points and therefore, for 21 samples formed a data matrix with dimension 21 × 555 (X-block). The PLS model was used to correlate X-block to Y-block, which was a concentration matrix of 13 PAHs in 21 calibration samples (21 × 13) using the PLS model. The number of significant latent variables (LVs) was determined according to the minimum value of root-mean square error of calibration (RMSEC) and cross-validation (RMSECV). Furthermore, statistical parameters of R-squared (R²), RMSEC, RMSECV and relative error in prediction (REP) were used for model validation. The developed model was validated both internally (by leave-one-out cross-validation, LOO-CV) and externally (by validation set). It is worth mentioning that the PLS model was validated using a validation set with a standard mixture of PAHs in the same concentration range as the calibration set, which had an X-block with dimensions 9 × 555 and a Y-block with dimensions 9 × 13. In addition, the potential of variable selection methods of RV, VIP and SR^23,24 were studied on the performance of PLSR modeling. Finally, three spiked water samples (from tap, well and farm) in three different concentration levels with an X-block with dimensions 9 × 555 and a Y-block with dimensions 9 × 13 were used to check the effect of sample matrix on the performance of the developed analytical procedure. Fig. 1 shows the general workflow of the proposed strategy in this study.

Fig. 1 General workflow of the proposed strategy in this work for the analysis of PAHs in water samples.

2.5. Instruments

Absorbance measurements were carried out with a Lambda 25 spectrophotometer (Perkin-Elmer, USA) using a 1.0 cm glass cell. Spectra were acquired in the wavelength range from 300 to 800 nm with a resolution of 1 nm.

The fluorescence spectroscopy was performed using a Cary Eclipse fluorescence spectrometer (Varian, USA) using a 1 cm × 1 cm quartz cell. All the spectra were recorded at room temperature.

TEM images were captured using a PHILIPS MC 10 TH microscope at an acceleration voltage of 100 kV.

Sample mixing and shaking was done by a Vortex 3, 2500 rpm (Raha Tajhiz Aria, Tehran, Iran). Centrifugation was performed with a Labofuge 1500 centrifuge (Heraeus, Germany) at the maximum rotational speed of 12 000 rpm.

The GC-FID analysis was carried out with an Agilent 7890A gas chromatograph (Agilent Technologies, CA, USA) equipped with a split/splitless injector. Separations were performed on a (5% phenyl)-methyl polysiloxane (DB-1) column (30 m length, 0.25 mm i.d., 0.25 μm film thickness). 2 μL of extract was injected to GC-FID using Hamilton GC syringe in splitless mode. The oven temperature program for the separation conditions was 100 °C for 1 min, followed by temperature increasing to 280 °C at 20 °C min⁻¹ and 20 min holding at 280 °C. The total run time was 30 min. The injector temperature was 270 °C. In all cases, the carrier gas was ultrapure helium at constant flow rate of 2 mL min⁻¹.

2.6. Software

An enhanced ChemStation software package G2070BA (Agilent Technologies, CA, USA) was used for data export. The design of experiments, model development and optimization were performed using a trial version of Design-Expert 7.1.5 (Stat-Ease Minneapolis, USA). All calculations regarding the univariate and multivariate calibration steps were performed in MATLAB 7.11.0 (Mathworks Inc., MA, USA). PLS Toolbox 5.8 (Eigenvector, USA) was used for PLSR modeling.

3. Results and discussion

3.1. AuNPs synthesis using Fren's method

As has been mentioned earlier, the AuNPs in this study were prepared by reducing HAuCl₄ with trisodium citrate by Fren's method.²⁶ Extraction efficiencies as a function of average particle size have been studied in previous literature.^12,13 In general, smaller particles were more efficient than larger particles for the extraction of PAHs due to their higher surface area. In other words, AuNPs smaller than 20 nm could not be precipitated by centrifugation, but kept their disperse nature in the supernatant phase. Therefore, AuNPs were prepared to an approximate size of 20 nm and characterized by UV-vis spectroscopy and their TEM images (Fig. 2).

Fig. 2 Characterization of AuNPs using (a) UV-vis spectrum and (b) TEM image.

Fig. 2a depicts the UV-vis spectrum of the synthesized AuNPs. The maximum absorption at 526 nm confirms the desired size of the nanoparticles (i.e., ∼20 nm).²⁶ In addition, full width at half maximum (FWHM) of ca. 80 nm is evidence of the narrow size distribution for the synthesized AuNPs. The TEM image of synthesized AuNPs is shown in Fig. 2b. As can be seen, the TEM image also confirms the AuNPs size and their narrow size distribution.

3.2. Selection of proper desorption and acceptor solvents

The extraction efficiency mainly depends on the selection of appropriate desorption and acceptor solvents. In this regard, several desorption solvents with strong binding affinity with gold were attempted for releasing PAHs from the AuNPs' surfaces into acceptor solvents, including toluene-3,4-dithiol, 1-ethanethiol, 1,2-ethanedithiol and 1,3-propanedithiol. The total peak areas of the 13 PAHs were used as the criterion for making a decision concerning the best solvent. Fig. 3a shows the obtained total peak areas for different desorption solvents. As it is evident from this figure, 1,3-propanedithiol has the maximum extraction efficiency, therefore, this solvent was used for subsequent analysis.

Fig. 3 Obtained total peak areas for (a) different desorption solvents and (b) different acceptor solvents.

Moreover, the organic acceptor solvent plays an important role in SPNE extraction efficiency. Density, polarity and affinity of target analytes with solvent were the main features considered for the acceptor solvents. In this context, lower density and polarity of acceptor solvents caused better separation of desorbed PAHs from water and AuNPs. Therefore, among different acceptor solvents (i.e., polar and nonpolar), n-octane, n-nonane and n-decane showed better performances. Fig. 3b shows the extraction efficiency obtained using these acceptor solvents. The best extraction efficiency was obtained with n-nonane and n-decane. Therefore, these two solvents can be used for SPNE as acceptor solvents. As the performance of n-nonane and n-decane have no significant difference (the difference was just 10 units among 1000 units of peak area and this difference was not significant according to the confidence interval (error bar) of the calculated peak areas), n-nonane was used for this study.

3.3. Multi-response optimization of extraction procedure

To achieve the highest possible performance, the SPNE efficiency was optimized using a CCD with five levels. According to our experiments, five factors including acceptor solvent volume (A), desorption solvent volume (B), methanol volume (C), adsorption vortex time (D), and desorption vortex time (E) were found to be significant for optimization. Table 1 shows the factors along with their units, abbreviations and levels.

Table 1 Effective factors on SPNE along with their units, abbreviations and levels for CCD

Factor	Abbreviation	Dimension	−α	−1	0	1	+α
Acceptor solvent volume	A	μL	15	35	55	75	95
Desorption solvent volume	B	μL	1	2	3	4	5
Methanol volume	C	μL	12	26	40	54	68
Adsorption vortex time	D	min	3	5	7	9	11
Desorption vortex time	E	min	3	5	7	9	11

---

Peak area of 13 PAHs was used to develop 13 individual models to correlate the peak area of each PAH with extraction parameters. In order to maintain homoscedasticity, a logarithmic transformation was applied to the responses.

Backward-MLR and ANOVA were used for model development. As an example, Table 2 shows the ANOVA table for Phen. The p-value for the model is <0.0001, which confirms the validity of the model; the p-value for the lack of fit (LOF) is 0.9142 and this indicates that it is not significantly relative to the pure error. Moreover, the p-value for blocking is 0.8446 and it shows that it is not significant. Therefore, the batch of synthesized AuNPs does not have any significant effect on the developed model for Phen.

Table 2 ANOVA table of quadratic response surface for Phen

Source	SS	DOF	MS	Fexp	p-Value
Block	0.0002	1	0.0002	0.038	0.8446	Not significant
Model	1.100	14	0.079	15.24	<0.0001	Significant
A	0.390	1	0.390	74.65	<0.0001
B	0.026	1	0.026	5.00	0.0368
C	0.079	1	0.079	15.22	0.0009
AB	0.072	1	0.072	13.98	0.0013
AC	0.073	1	0.073	14.19	0.0012
BC	0.018	1	0.018	3.48	0.0770
BD	0.049	1	0.049	9.38	0.0061
BE	0.031	1	0.031	6.02	0.0235
CD	0.064	1	0.064	12.44	0.0021
CE	0.037	1	0.037	7.09	0.0150
DE	0.110	1	0.110	22.12	0.0001
A^2	0.092	1	0.092	17.69	0.0004
C^2	0.038	1	0.038	7.31	0.0137
D^2	0.025	1	0.025	4.78	0.0409
Residual	0.100	20	0.0052
Lack of fit	0.040	12	0.0034	0.42	0.9142	Not significant
Pure error	0.063	8	0.0079
Corrected total	1.210	35

---

As a result, the following quadratic polynomial model (eqn (1)) was obtained:

log₁₀(Phen) = +1.38 − 0.13A + 0.033B − 0.057C − 0.067AB + 0.068AC + 0.034BC + 0.055BD + 0.034BE − 0.063CD + 0.048CE + 0.085DE + 0.053A² + 0.034C² + 0.028D² (2)

In a similar way, the peak areas for other PAHs were also modeled as a function of extraction parameters and finally 13 individual models were obtained. ANOVA tables of the rest of the PAHs are presented in Tables S1–S11 (see ESI†). Table 3 shows the statistical parameters for the model of Phen thus developed.

Table 3 Statistical parameters for the developed quadratic model of Phen

Statistic	Value	Statistic	Value
R^2	0.9143	S/N	19.390
Adjusted-R^2	0.8543	CV%	4.93
Predicted-R^2	0.7523	PRESS	0.30

---

The statistical parameters R², adjusted-R² and predicted-R² are 0.9143, 0.8543 and 0.7523, respectively, which confirm the validity of the developed model. In addition, the values of adequate precision (S/N), coefficient of variation (CV) and prediction error sum of squares (PRESS) are 19.39, 4.93 and 0.30, respectively, which are acceptable. In general, the abovementioned statistical parameters for 13 models were in the ranges as follows: R²: 0.8156–0.9143, adjusted-R²: 0.7324–0.8543, predicted-R²: 0.6543–0.7523, S/N: 12.46–19.39, CV: 3.56–5.45, and PRESS: 0.20–0.60.

For the simultaneous optimization of 13 developed models and to obtain the global optimum values of effective parameters on the SPNE procedure, multi-response optimization using Derringer's desirability function (D) and downhill simplex were used.²⁸ The maximum D value (found using simplex optimization method) was 0.945. The optimum extraction parameters were 15.31 μL acceptor solvent volume (A), 4.53 μL desorption solvent volume (B), 43.77 μL methanol volume (C), 7.22 min adsorption vortex time (D), and 9.63 min desorption vortex time (E). The 3D response surfaces obtained for the global desirability function are shown in Fig. 4.

Fig. 4 The 3D response surfaces obtained for the global desirability function versus (a) methanol and nonane volumes and (b) adsorption and desorption vortex times.

For example, Fig. 4a shows the changes of global desirability function (D) versus methanol and n-nonane volumes. Changes in D for adsorption and desorption vortex times are shown in Fig. 4b.

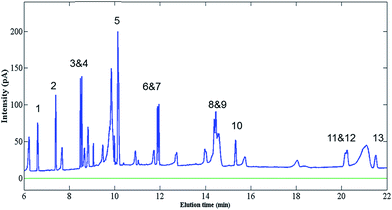
Finally, the SPNE procedure and chromatographic analysis were repeated three times (n = 3) at optimum conditions and the obtained responses for developed models were compared with the experimental ones. The relative errors for predicted and real peak areas were below 10.0% and all of them were within confidence limits (confidence level 95%). Fig. 5 shows the GC-FID chromatogram for 13 PAHs in optimum SPNE conditions in concentration level of 50 ng mL⁻¹.

Fig. 5 GC-FID chromatogram for 13 PAHs in optimum SPNE conditions in concentration level of 50 ng mL⁻¹. Peaks numbers are respectively Aceny (1), Flu (2), Phen (3), Ant (4), Pyr (5), B[a]A (6), Chr (7), B[b]F (8), B[k]F (9), B[a]P (10), B[ghi]P (11), I[1,2,3-cd]P (12), and DB[ah]A (13).

3.4. Univariate calibration

After optimizing the extraction procedure, an external calibration strategy was used to build calibration curves and to obtain analytical figures of merit (AFOMs) of the target PAHs. In this respect, a conventional univariate calibration approach was taken into account using the peak areas of 13 PAHs. The calibration set contained 21 samples in seven different concentration levels. Table 4 shows the univariate calibration parameters for 13 PAHs.

Table 4 Univariate analytical figures of merit using external calibration strategy for 13 PAHs

PAHs	SEN	γ	R^2	LODstat (ng mL^−1)	LODexp (ng mL^−1)	LDR	RE	RSD	SEP	RMSEP	sy/x	sm
Aceny	1.17	2.90	0.999	1.03	0.032	1.03–70.0	3.49	2.72	0.48	0.43	0.40	0.011
Ant	5.62	0.99	0.995	3.02	0.021	3.02–70.0	2.69	2.66	1.88	1.71	5.65	0.193
Phen	1.32	0.63	0.994	4.75	0.211	4.48–70.0	2.71	1.77	2.21	1.97	2.09	0.057
Flu	0.94	1.08	0.997	2.79	0.084	2.79–70.0	3.01	8.97	1.55	1.41	0.87	0.026
Pyr	6.63	3.04	0.999	0.99	0.012	0.99–70.0	3.97	0.74	0.58	0.53	2.18	0.066
B[a]A	2.86	5.01	0.999	0.60	0.026	0.60–70.0	4.24	2.49	0.30	0.27	0.57	0.016
Chr	0.58	0.74	0.997	4.04	0.203	4.04–70.0	3.79	1.54	2.18	1.99	0.78	0.015
B[b]F	0.77	0.86	0.997	3.49	0.454	3.49–70.0	0.74	4.96	1.71	1.53	0.89	0.024
B[k]F	0.38	0.69	0.998	4.37	0.375	4.37–70.0	1.60	2.71	2.16	1.93	0.56	0.011
B[a]P	0.46	0.86	0.999	3.50	1.034	3.50–70.0	4.21	0.79	1.74	1.59	0.53	0.010
I[123-cd]P	0.28	0.98	0.998	3.06	1.250	3.06–70.0	5.38	0.04	1.48	1.32	0.28	0.058
DB[a,h]A	0.26	0.96	0.998	3.13	1.250	3.13–70.0	5.84	0.06	1.56	1.42	0.27	0.0052
B[g,h,i]P	0.29	0.86	0.998	3.51	0.968	3.51–70.0	1.17	0.07	1.89	1.85	0.34	0.006

---

Calibration sensitivity (SEN), analytical sensitivity (γ), regression coefficient (R²), linear dynamic range (LDR), limit of detection (LOD) (S/N = 3) are the main AFOMs considered in this study. In addition, different error expressions, such as relative error of calibration concentrations (RE), relative standard deviation (RSD), standard error of prediction (SEP), and root-mean square error of prediction (RMSEP), standard deviation of calibration (s_y/x) and standard deviation of slope (s_m) were used to evaluate the developed calibration model. According to this table, the SEN values are in the range of 0.26–5.62. Also, the values of γ are in the range of 0.69–5.01. It should be noted that γ is calculated using the value of standard deviation of the calibration (s_y/x). Other statistical parameters for the calibration, including R² of calibration equations (0.994–0.999), RE (0.74–5.84%), RSD (0.04–8.97%), SEP (0.30–2.21), RMSEP (0.27–1.99) are also reasonable according to the complexity of the samples. The LOD for any analytical procedure is the point at which analysis is just feasible and may be determined by a statistical or an experimental approach. In Table 4, there are two columns showing calculated LOD using two different approaches. The statistical approach is based on measuring replicate blank samples and the mean and standard deviation (SD) are calculated. The LOD is 3.28 SD divided by the calibration sensitivity (slope of calibration curve).^29–31 In other words, the experimental approach consists of analyzing a series of samples containing increasingly lower concentrations of the analyte. The LOD is the lowest concentration at which the results still satisfy some predetermined acceptance criteria.^29–31 Surprisingly, the results of two approaches are significantly different. As can be seen, the calculated LOD values by the conventional method (LOD_exp) are lower than the ones calculated by the statistical approach (LOD_stat) even by two orders of magnitude. In this regard, the empirically determined LOD values for 13 PAHs underestimated the LOD because of the large imprecision associated with this method. The possible reason for this difference is related to the consideration of standard deviation of calibration, slope and intercept in the statistical approach, which is not considered in the conventional method. As a consequence, the statistical approach provided much more realistic LOD values.

3.5. Multivariate calibration

The raw GC-FID chromatogram for one of the calibration samples is shown in Fig. 5. As shown in this figure, there is heavy overlap between chromatographic peaks of the 13 PAHs. Therefore, using univariate calibration for modeling and prediction of PAH concentrations in real samples may not be a good strategy. In this context, multivariate calibration using PLSR may address this complex situation. At first, the PLSR model was applied to develop a multivariate model using calibration set data. The X- and Y-block data sets were prepared before any PLS modeling using different pre-processing methods.³² For the current study, mean-centring for Y-block and autoscaling for X-block were chosen as the most proper methods. Moreover, only chromatographic regions containing the target analytes were kept, and other chromatographic regions with noisy elution profiles and intensity outside of the range of the instrument were eliminated. Furthermore, elution time shifts between different chromatographic runs were corrected using a correlation optimized warping (COW) method.^33,34 In this regard, the slack parameter and segment length of the COW algorithm were set to 2 and 26, respectively.

In order to select the number of factors in PLS modeling, the minimum value of RMSE in the plot of RMSE of calibration (RMSEC) in red and RMSE of cross-validation (RMSECV) in blue versus number of LVs was used (Fig. 6). It is important to note that using LOO-CV helps us to select the significant number of components in the model and therefore, to avoid model overfitting. In addition, the validation set with nine samples (Section 2.4) also was used to confirm the number of PLS components. All of these methods confirmed the presence of 6 PLS components.

Fig. 6 Plot of RMSE of PLS model for calibration (RMSEC, red) and cross-validation (RMSECV, blue) versus the number of LVs.

In addition, Table 5 shows the explained variance in X- and Y-blocks using 6 LVs for the calibration set.

Table 5 Percent variance captured by PLS model

LV	X-Block		Y-Block
	Individual	Total	Individual	Total
1	25.72	25.72	74.35	74.35
2	29.81	55.53	17.51	91.86
3	11.73	67.26	4.92	96.79
4	8.20	75.46	1.84	98.62
5	10.68	86.14	0.38	99.01
6	2.56	88.70	0.40	99.41

---

Moreover, the statistical parameters of RMSE and R² were used for evaluation of the developed PLS model. The PLS model with 6 LVs had RMSEC of 1.47 and RMSECV of 5.62 for the calibration set. In other words, for the validation set the value of RMSE was 6.45. The values of R² for calibration, cross-validation and validation were 0.9964, 0.9510 and 0.9413, respectively. Even after eliminating chromatographic regions with no meaningful variables, chromatographic fingerprints still contain over one thousand variables, of which most do not have any desirable information. Thus, the performance of the three well-known variable selection methods of RV, VIP, and SR were compared. Fig. 7 depicts the selected variables by each method. It is important to note that predictive and interpretive abilities of the developed PLSR models were two important aspects in the evaluation of the different variable selection methods.

Fig. 7 Selected variables by different variable selection methods of (a) RV, (b) VIP and (c) SR for PLS modeling.

Using RV is one of the conventional ways to rank the variables based on their importance for PLSR. The PLSR model gives one vector (RV) for each selected component (Fig. 7a). The calculated VIP scores for chromatographic data points are shown in Fig. 7b. As it is suggested, the points by VIP scores higher than one were chosen as the important variables in this method. In other words, the high value of SR for a variable means that variable has a strong prediction ability. To have better insight into the results, a threshold equal to 0.4 was chosen to select the most important variables (Fig. 7c). As can be seen, the three variable selection methods choose almost the same variables. Table 6 compares different PLSR variable selection methods in terms of RMSE and R² for calibration, cross-validation and validation sets.

Table 6 Statistical parameters of PLS model using different variable selection methods

Variable selection	No. of LVs	RMSE		Validation	R^2		Validation
		Calibration	CV		Calibration	CV
None	6	1.47	5.62	6.45	0.9964	0.9510	0.9413
RV	6	1.27	5.28	6.15	0.9973	0.9655	0.9492
VIP	6	2.27	6.47	7.12	0.9915	0.9348	0.9289
SR	6	3.94	13.53	14.43	0.9743	0.7100	0.6945

---

As can be seen, the numbers of considered LVs are the same for the three methods (i.e., 6 LVs). The values of RMSE and R² for calibration, LOO-CV as internal validation and external validation set, confirm better performance of RV than other methods for almost all analytes. Therefore, this method was used as the variable selection method of PLS modeling in spiked sample analysis.

3.6. Spiked water samples

The applicability domain of the developed method, in this study, was tested to quantify the target analytes in three different water samples (from tap, well and farm water). For this purpose, the samples were spiked with the PAHs standard mixture at concentration levels of 2, 5 and 20 ng mL⁻¹ and analyzed according to the procedure (Section 2.3) under the optimized conditions (n = 3). As an example, Fig. 8 shows the GC-FID chromatograms for the non-spiked farm water sample (chromatogram a). GC-FID chromatograms of farm water sample in three different spiked concentrations (2, 5, 20 ng mL⁻¹) are also shown (chromatograms b–d).

Fig. 8 GC-FID chromatograms of (a) unspiked farm water sample and spiked in three different PAHs concentrations (b) 2, (c) 5, and (d) 20 ng mL⁻¹. Peak numbers are for: Aceny (1), Flu (2), Phen (3), Ant (4), Pyr (5), B[a]A (6), Chr (7), B[b]F (8), B[k]F (9), B[a]P (10), B[ghi]P (11), I[1,2,3-cd]P (12), and DB[ah]A (13).

The GC-FID data for the test set was arranged in a two-dimensional array (matrix) of 9 × 555. The same preprocessing methods as the calibration set (i.e., autoscaling of X-block and mean centering of Y-block) were used before PLS modeling for the test set. In addition, elution time shifts were corrected using the COW method. Furthermore, the PLS RV method was used for variable selection. Table 7 shows the relative recoveries (RRs) and relative standard deviations (RSDs) for 3 replicate determinations of the PAHs in tap, well and farm water samples. The obtained RRs (%) were in the range of 76.2–101.2 for tap water, 78.4–104.2 for well water and 74.3–100.2 for farm water. Also, the RSDs (%) were 1.56–6.93 for tap water, 1.89–7.46 for well water and 2.56–8.89 for farm water.

Table 7 The obtained values of RR (%) and RSD (%) for spiked tap, well and farm water samples

	Added	Tap water		Well water		Farm water
		RR	RSD	RR	RSD	RR	RSD
Aceny	2	83.5	3.78	86.2	4.94	85.2	4.78
	5	79.6	5.67	84.3	5.39	83.2	6.67
	20	82.1	4.54	87.2	5.11	88.1	5.54
Ant	2	83.2	3.26	82.1	3.78	79.2	4.26
	5	83.4	4.62	86.0	2.79	83.1	5.62
	20	81.5	5.04	84.0	6.31	81.8	6.04
Phen	2	86.9	2.67	90.2	1.89	90.1	2.67
	5	84.6	4.02	89.2	4.86	86.2	5.02
	20	82.6	3.87	87.3	5.23	87.3	4.87
Flu	2	94.3	4.56	93.2	4.67	92.1	5.56
	5	92.2	6.02	95.4	4.43	93.6	7.02
	20	93.3	5.54	96.3	5.67	91.7	6.54
Pyr	2	78.3	1.87	82.1	4.21	80.2	3.87
	5	76.2	2.62	78.4	4.59	74.3	4.62
	20	78.4	3.49	84.2	6.39	75.3	5.49
B[a]A	2	99.1	3.21	98.2	2.56	97.2	5.21
	5	97.4	2.90	104.2	5.37	98.2	4.90
	20	98.6	4.66	96.4	4.66	95.8	7.66
Chr	2	93.2	4.56	98.2	1.98	89.1	4.56
	5	92.8	5.31	96.3	4.73	91.3	7.31
	20	91.5	6.93	92.5	3.55	92.2	6.93
B[b]F	2	94.3	2.78	95.3	3.67	96.1	3.78
	5	92.2	5.13	96.1	5.65	93.2	7.13
	20	95.1	3.69	95.3	6.27	94.7	5.69
B[k]F	2	93.1	3.65	92.7	5.21	92.6	4.65
	5	89.2	4.89	92.2	4.95	90.5	8.89
	20	92.6	4.56	89.7	6.48	90.2	6.56
B[a]P	2	98.4	4.32	97.2	6.32	92.1	4.32
	5	97.4	6.21	104.0	5.75	93.6	7.21
	20	95.5	5.54	102.6	7.31	95.1	5.54
I[123-cd]P	2	89.2	1.67	94.3	3.21	88.9	3.67
	5	84.6	4.32	97.0	6.28	86.2	6.32
	20	86.3	2.69	92.4	4.95	87.3	7.69
DB[a,h]A	2	101.2	1.56	94.5	4.90	97.3	2.56
	5	99.4	3.19	99.2	5.27	100.2	3.19
	20	96.2	2.15	96.4	7.11	98.2	4.15
B[g,h,i]P	2	90.3	4.32	91.5	5.89	91.4	4.32
	5	87.4	5.37	93.2	6.87	93.2	6.37
	20	91.4	4.53	87.8	7.46	90.4	4.83

---

Inspection of the results confirms the validity of the proposed multivariate strategy combined with SPNE-GC-FID for simultaneous determination of PAHs in complex sample matrices.

4. Conclusion

Obtaining useful chemical information from chromatographic analysis of PAHs in different complex environmental samples is a challenging and active research field, which needs the attention of both analytical chemists and chemometricians. The great complexity of the samples that currently need to be analyzed in analytical chemistry calls every day for more sophisticated instrumentation and mathematical tools to accomplish the goal. In the present study, the use of SPNE-GC-FID combined with multivariate chemometric methods was proposed to develop a simple, efficient and low-cost approach for simultaneous determination of carcinogenic PAHs in complex water samples. For this purpose, CCD and multi-response optimization were used to optimize the SPNE procedure. The PLS method was then used for multivariate calibration of 13 EPA-PAHs in calibration and test sets in the presence of baseline/background contribution and other interferences. Finally, the AFOMs were calculated for target analytes. The successful application of this combined strategy for the analysis of standard and spiked water samples confirmed the applicability of this new approach for complex environmental samples.

Acknowledgements

The authors would like to thank Iran National Science Foundation (INSF) for financial support of the research project entitled: “Simultaneous determination of carcinogenic aromatic pollutants in environmental samples using gold nanoparticles and multivariate chemometric techniques” (Project No. 94009575) (http://www.insf.org).

References

1. K. Tamakawa, in Comprehensive Analytical Chemistry, ed. P. Yolanda, Elsevier, 2008, vol. 51, pp. 599–651.
2. M. Tobiszewski and J. Namieśnik, Environ. Pollut., 2012, 162, 110–119.
3. H. Parastar, J. R. Radović, M. Jalali-Heravi, S. Diez, J. M. Bayona and R. Tauler, Anal. Chem., 2011, 83, 9289–9297.
4. M. Ahmadvand, H. Sereshti and H. Parastar, J. Chromatogr. A, 2015, 1413, 117–126.
5. J. Płotka-Wasylka, N. Szczepańska, M. de la Guardia and J. Namieśnik, Trends Anal. Chem., 2016, 77, 23–43.
6. J. Li, Y.-B. Wang, K.-Y. Li, Y.-Q. Cao, S. Wu and L. Wu, Trends Anal. Chem., 2015, 72, 141–152.
7. A. Mehdinia and M. O. Aziz-Zanjani, Trends Anal. Chem., 2013, 51, 13–22.
8. J. Tian, J. Xu, F. Zhu, T. Lu, C. Su and G. Ouyang, J. Chromatogr. A, 2013, 1300, 2–16.
9. E. Guihen, Trends Anal. Chem., 2013, 46, 1–14.
10. V. Amendola, M. Meneghetti, M. Stener, Y. Guo, S. Chen, P. Crespo, M. A. García, A. Hernando, P. Pengo and L. Pasquato, in Comprehensive Analytical Chemistry, ed. V. Miguel and I. L.-L. Ángela, Elsevier, 2014, vol. 66, pp. 81–152.
11. D. Hühn and W. J. Parak, in Comprehensive Analytical Chemistry, ed. V. Miguel and I. L.-L. Ángela, Elsevier, 2014, vol. 66, pp. 153–206.
12. H. Wang and A. D. Campiglia, Anal. Chem., 2008, 80, 8202–8209.
13. W. B. Wilson, U. Hewitt, M. Miller and A. D. Campiglia, J. Chromatogr. A, 2014, 1345, 1–8.
14. F. Busetti, A. Heitz, M. Cuomo, S. Badoer and P. Traverso, J. Chromatogr. A, 2006, 1102, 104–115.
15. A. Meudec, J. Dussauze, M. Jourdin, E. Deslandes and N. Poupart, J. Chromatogr. A, 2006, 1108, 240–247.
16. D. L. Poster, M. M. Schantz, L. C. Sander and S. A. Wise, Anal. Bioanal. Chem., 2006, 386, 859–881.
17. M. Jalali-Heravi, H. Parastar and H. Ebrahimi-Najafabadi, J. Chromatogr. A, 2009, 1216, 6088–6097.
18. E. Martendal, D. Budziak and E. Carasek, J. Chromatogr. A, 2007, 1148, 131–136.
19. M. A. Bezerra, R. E. Santelli, E. P. Oliveira, L. S. Villar and L. A. Escaleira, Talanta, 2008, 76, 965–977.
20. H. Parastar, Analyst, 2014, 139, 2574–2582.
21. H. Parastar and R. Tauler, Anal. Chem., 2014, 86, 286–297.
22. J. M. Amigo, T. Skov and R. Bro, Chem. Rev., 2010, 110, 4582–4605.
23. P. Geladi and B. R. Kowalski, Anal. Chim. Acta, 1986, 185, 1–17.
24. S. Wold, M. Sjöström and L. Eriksson, Chemom. Intell. Lab. Syst., 2001, 58, 109–130.
25. I. G. Chong and C. H. Jun, Chemom. Intell. Lab. Syst., 2005, 78, 103–112.
26. S. Basu, S. K. Ghosh, S. Kundu, S. Panigrahi, S. Praharaj, S. Pande, S. Jana and T. Pal, J. Colloid Interface Sci., 2007, 313, 724–734.
27. S. Eustis, PhD Thesis, Georgia Institute of Technology, 2006, pp. 56–57.
28. N. R. Costa, J. Lourenço and Z. L. Pereira, Chemom. Intell. Lab. Syst., 2011, 107, 234–244.
29. D. A. Armbruter, M. D. Tillman and L. M. Hubbs, Clin. Chem., 1994, 40, 1223–1238.
30. M. E. Zorn, R. D. Gibbson and W. C. Sonzogni, Environ. Sci. Technol., 1999, 33, 2291–2295.
31. R. Gabriels, Anal. Chem., 1970, 42, 1439–1440.
32. S. Wold, J. Trygg, A. Berglund and H. Antti, Chemom. Intell. Lab. Syst., 2001, 58, 131–150.
33. N.-P. V. Nielsen, J. M. Carstensen and J. Smedsgaard, J. Chromatogr. A, 1998, 805, 17–35.
34. G. Tomasi, F. van den Berg and C. Andersson, J. Chemom., 2004, 18, 231–241.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra18415d

---