Isoelectronically doped CdSe/Te nanoalloys as alternative solar cell materials: insight from computational analysis

Abstract

Nanocrystals play an important role in various fields of technology, especially in catalysis, optoelectronics, bio-diagnostics, magnetic sensing, etc. These materials are more demanding as their optoelectronic properties can be fine-tuned by external doping and also by varying the dopant composition. Herein, we take the advantages of SCC-DFTB methods and investigate the effects of substitution of Se by Te atoms on the structure and electronic properties of the CdSe_1−xTe_x nanoalloys of different compositions. It has been observed that, incorporation of bigger Te atoms induces structural strain which has a great impact on the overall electronic structure of the CdSe/Te nanoalloys. The charge distributions in the frontier molecular orbitals clearly indicate spatial separation of the electrons and holes in some nanoalloys which promise their potential applications in optoelectronic devices.

---

1. Introduction

Nanoparticles have received much attention in the field of materials science because of their fascinating physico-chemical properties that are dramatically different from their bulk counterparts.¹ This is induced by the significant amount of surface atoms, which have distinct structural and electronic properties compared to the bulk ones, an outcome caused by coordination imperfections. Among nanoparticles with different bonding natures, semiconductor nanocrystals, with the tunability of their electronic and optical properties by the three-dimensional confinement of carriers, have attracted considerable interest.² Semiconductor nanocrystals (NCs) possess great scientific and technological prospects due the ability to engineer their optical properties by the variation of size, shape, and surface properties.^3,4 By utilizing the recent progress in a colloidal synthetic route, one can synthesize semiconductor NCs in a desired way.^5–8 So, proper utilization of a semiconductor NC with a desirable property has now become an open hand practice to the scientists. A large number of II–VI^9–14 and III–V^15–17 semiconductor NCs have been prepared over the past two decades. These NCs are good candidates for electronic and optical devices due to their reduced dimensions enabling one to reduce the size of electronic circuitry.¹ Also, due to the increased oscillator strengths in these NCs as a result of quantum confinement, these are expected to have higher quantum efficiencies in applications such as light emission.^18–20 This is a direct consequence of a greater overlap between the electron and the hole wavefunctions upon size reduction. Moreover, one can tune these properties to suit a specific application by merely changing the size of the nanocrystals. For example, the band gap of CdSe can be varied from 1.9 eV to 2.7 eV by changing the size of the particle from 5.5 nm to 2.3 nm.²¹ Alongwith the band gap of the particle, the photoluminescence can also be varied through the red to the blue region of the visible spectrum.^22,23

New strategies are now being adopted relating to composition control properties of NCs which include impurity doping, alloying, formation of core/shell heterostructures, etc. Doping introduces localized states in between the band gap region of the NCs and thus governs the optical properties of the host NCs.^20,24–26 In a core/shell heterostructure,^13,27 an over-coating is made over a narrow band-gap semiconductor with another semiconductor material having a wider band gap, that ensures efficient confinement of electron–hole pairs in the core, leading to significant improvement of the photoluminescence quantum efficiency.^8,28 The third route for composition control of NCs is through alloying.^8,18,29 Obviously, alloyed nanoparticles show different structural and physical properties in comparison to their mother compounds.^30–32 There is an enhancement in specific properties in many cases upon alloying of metallic QDs which led to widespread applications in electronics, engineering and catalysis.¹⁸ For a variety of alloyed II–VI semiconductors, the band gap varies almost linearly between the band-gaps of the pure materials according to the composition.^18,24 For these heterostructures, electrons and holes are driven to separate into different region of the particles (e.g., cores and shells), making them interesting for applications in photovoltaics.²⁴ Alloyed composition of semiconductor NCs opens up additional perspectives in engineering materials with different electronic and optical properties. In particular, the absolute energy values of conduction and valence bands can precisely be tuned not only by size of the NCs but also by degree of alloying.⁸ In fact, analogous to the magic sizes³³ of the nanoalloys they also display magic compositions, i.e., the compositions at which the alloyed nanoclusters present a special stability. Surface structures, compositions, and segregation properties of nanoalloys are important in determining chemical reactivity and especially catalytic activity.^34–36 It has been experimentally observed that, for many common cation alloyed NCs like CdSe_xS_1−x, CdSe_xTe_1−x, etc. the band gap shows a bowing nature instead of linearity.^{8,20,22,37–39} The deviation from linearity depends on the difference in electro negativity of the two end components. Nonlinear dependence of the band-gap of CdSe_xTe_1−x NCs on composition makes this alloy a desirable candidate for applications in a hybrid NC-polymer solar cell with the purpose of enhancing the power conversion efficiency.^39–41 The superiority of the nanoalloys comes from their wider absorption band, higher conduction band edge, and better chemical stability in comparison to their constituents.^39,42–44

From a theoretical point of view, studying of nanoalloys is a fascinating challenge due to the complexity of their energy landscape. Very recent experiment⁴¹ shows that the valence band edge of CdSe_1−xTe_x exhibits a very weak dependence on ‘x’ for values below 0.5 indicating that the decrease in the optical band gap is mainly due to the decrease in the conduction band edge energy. However, for x > 0.5, both the conduction and valence band edges shift to higher values with an overall increase in the band gap. The experimental trends show that the characteristic red shift of the band gap with low to intermediate Te content (x < 0.5) is determined by relaxation of the lattice constant, whereas for x > 0.5, it is mainly contributed from the difference in electro negativity of the anions.⁴¹ As these nanoalloys are superior to their constituents (CdSe and CdTe) for solar energy harvesting process,³⁹ a proper theoretical knowledge is required for tailoring their photophysical properties so as to utilise them as a better sensitizer. Herein, we employ self consistence charge density functional tight binding (SCC-DFTB) method with the derived set of parameters to compute the fundamental properties like stability, band edge energies and wavefunctions, Mulliken charge, etc. to have a better insight on the optoelectronic properties of the nanoalloys.

2. Model and computation

In the present work we have employed the self-consistent charge density-functional tight-binding (SCC-DFTB) method^45–49 to study the electronic structure of the CdSe_1−xTe_x nanoalloys as a function both size and composition. The SCC-DFTB method compromises accuracy and computational efficiency quite effectively and it is one of the most promising approaches in treating systems composing large number of atoms. The method is basically a parametrized DFT scheme, the total energy of which is expressed as a second order expansion of the DFT Kohn–Sham total energy with respect to charge density fluctuations.^46,48 We have used Slater-type orbitals (STOs) as basis sets and Perdew–Burke–Ernzerhof (PBE)⁵⁰ exchange correlation energy functional and our recently derived SCC-DFTB parameter set.⁵¹ In one of our previous studies we have established the accuracy of our derived SCC-DFTB parameter set for Cd-chalcogenides and their interaction with several different systems by calculating several physical parameters (viz. the lattice constants, cohesive energy, band gap) and electronic structure of materials of various dimensions.^51–53 The close agreement between our parametrized SCC-DFTB and standard ab initio results strengthen the belief that the derived parameter set is reliable to study the Cd-chalcogenide nanostructures.⁵¹ For modelling the nanocrystals, we take wurtzite CdSe bulk structure and then cut the almost spherical stoichiometric quantum dots of different diameters. These are then allowed to relax within a suitable vacuum region using conjugate gradient algorithm, until all forces become smaller than 0.001 eV Å⁻¹. All the calculations were done by using DFTB+ program suite⁴⁹ along with our derived sets of parameters.⁵¹ The doped nanoalloys were designed by properly replacing Se atoms by Te (replacements were done from outer region to inner region) and the corresponding structures were optimized using same procedure as mentioned above.

3. Results and discussion

3.1. Structure and stability

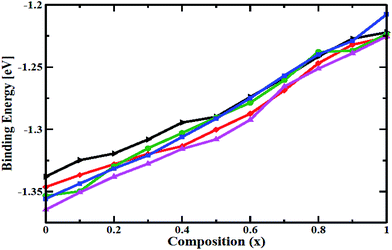
Let us first discuss the structural stability of the individual nanocrystals and the effect of alloying on them. For doing so, initially we took CdSe nanocrystals of different sizes and then substituting the Se atoms gradually by more electro positive Te atoms to form the nanoalloys of different compositions. It should be pointed out that, nanoalloys are chemically more stable than their constituents because of hardened lattice structure and lower rate of interdiffusion.^54,55 However, thermodynamic stability of the nanoalloys largely depends on the relative size of the dopant atoms. Fig. 1 represents the optimized geometry of some nanoalloys where surface dangling bonds are saturated by –OH (in case of Cd atom) or by –H (in case of Se and/or Te atom) groups. Although zinc-blende structure is the energetically preferred phase of bulk CdSe or CdTe at normal temperature and pressure, the relative stability of zinc-blende and wurtzite structures in the nano dimension may depend on the size of the nanoparticles.^37,41,56,57 Sarkar et al.⁵³ showed that binding energy of nanoalloys depends on the size as well as morphology; however, an overall trend of an increasing binding energy is observed when the cluster size increases. Motivated from the above findings, in the present work, we only consider the clusters derived from wurtzite lattice. To interpret the relative stability of the clusters we have calculated the binding energy for the individual clusters. The binding energy (per pair of atoms) of surface passivated nanoalloy of molecular formula Cd_mTe_nSe_(m−n) (OH)_pH_p is given by eqn (1).

E_b = [E_tot − (m_Cdμ_Cd + n_Teμ_Te + (m − n)_Seμ_Se + p_OHμ_OH + p_Hμ_H)]/N (1)

where, N = number of pairs of CdSe and/or CdTe and m/n/p_i denotes the number of ith species present in the nanoalloy and μ_i is the corresponding chemical potential of the species. It should be pointed out that the chemical potential of the elements are obtained from their corresponding bulk values and those of H and OH are calculated from the chemical potentials of gaseous H₂ and H₂O, respectively.

Fig. 1 Optimized geometries of (a) Cd₁₁₇Se₁₁₇, (b) Cd₁₁₇Se₈₁Te₃₆, (c) Cd₁₁₇Se₅₇Te₆₀, (d) Cd₁₁₇Se₃₃Te₈₄, and (e) Cd₁₁₇Te₁₁₇ nanoalloys. The yellow, magenta, green, red and grey balls correspond to the Cd, Se, Te, O and H atoms respectively.

Fig. 2 represents the variation in the binding energy as a function of composition for different nanoalloys. It is clear from the figure that the binding energy increases as the cluster size increases – indicating that, the biggest cluster has the highest stability. This can be taken as a direct consequence of the reduction in the ratio of surface to bulk atoms.^12,14,53 However, it should be mentioned that the binding energy of the individual clusters decreases with increasing concentration of the dopant Te atom which can be attributed by the fact that, incorporation with of more electropositive and bigger size Te atom creates lattice mismatch and induces strain in the cluster. But, on the other hand it is also observed that by introducing the dopant atom (here, Te in case of CdSe cluster) the relative stability of a particular cluster lie within the range of pure CdSe and CdTe nanocluster of that particular size. This observation ensures the formation of the doped clusters and in turns demands the practical realizations of the nanoalloys.

Fig. 2 Variation of binding energy as a function of composition of the nanoalloys of different sizes. Here black, red, green, blue and magenta lines represent 56–56, 66–66, 87–87, 105–105, 117–117 cluster sizes, respectively.

3.2. Band-edge energies and wavefunctions

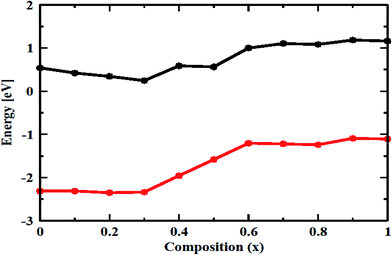
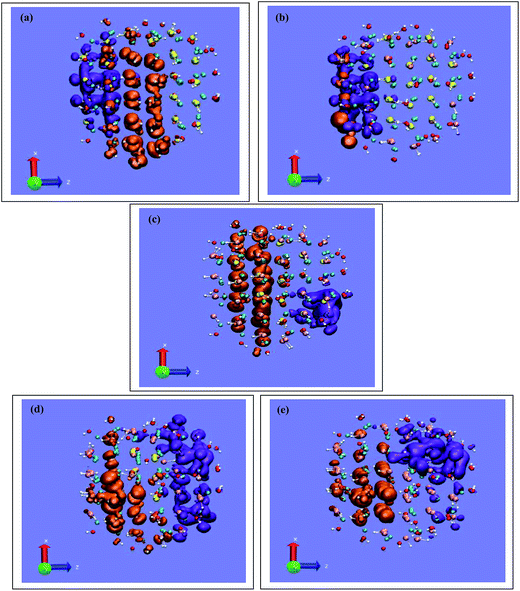
In this part we will focus on how variation of alloying on the individual clusters modifies the band edge energy and density of states of the CdSe_1−xTe_x nanoalloys. It is known that, due to the presence of a high degree of unsaturation in bare cluster, the structural relaxation alone cannot open the HOMO–LUMO gap because of the presence of surface states contributed from the unsaturated atoms on the cluster surface. But, once the surface atoms are passivated, the surface states are removed and consequently there opens the HOMO–LUMO gap. As for example, –SH passivated Cd₅₆Te₅₆ cluster shows an HOMO–LUMO energy gap of 2.02 eV, whereas that of the corresponding bare cluster is 1.31 eV only. Considering the above fact, here in the present study we only consider the passivated clusters and studied the variation of HOMO–LUMO gap as a function of cluster size and degree of alloying, as shown in Fig. 3. Analysis of the figure clearly indicates that in case of pure CdSe nanocrystal, the energy gap is minimum (=2.50 eV) for the smallest cluster size of Cd₅₆Se₅₆. The energy gaps for the bigger clusters are higher than 2.50 eV, however, the relation is not linear as there involve some other guiding factors like shape and symmetry of the nanoalloys. Interestingly, upon incorporation of Te atom in place of Se atom, it shows an overall decreasing trend of band gap with some bowing effect.⁴¹ This nonlinear dependence of the band-gap for the nanoalloys may be properly utilized for enhancing the power conversion efficiency in hybrid solar cell.^39,40 For all the studied clusters we observe that the energy gap gradually decreases with increasing the Te content up to 50% where it achieves the minimum energy gap, thereafter the energy gap increases until it reaches to the value corresponding to the energy gap of pure CdTe nanocrystal. This observation matches excellently with the experimental finding of Hou et al.⁴¹ who observed a strong red shift in the absorption and luminescence spectra for the quantum dots with average diameter of 4.5 ± 0.2 nm. Now, one should have a clear understanding behind this red shift. As can be seen in Fig. 4, up to 30% composition of Te, the HOMO energy of the nanoalloy remains almost at the same position, while that of LUMO goes down. With further increase in the composition of Te up to 50%, the LUMO energy remains same but the HOMO energy goes up quite rapidly thereby decreasing the energy gap very fast. Thus, the strong red shift in the luminescence spectra may be ascribed as the decreasing LUMO energy of the nanoalloys with Te composition below 30%. This result strongly corroborate with the sequence of the valence band edge energy calculated from the half-wave potential of the first anodic current inflection as obtained from cyclic voltammetric experiment.⁴¹ In between 30% and 50%, however, the situation is somewhat different; our calculation predicts that, here, the increase in HOMO energy precedes over the increase in LUMO energy. In any case, experimentally observed red-shift is strongly corroborated with the theoretically predicted HOMO–LUMO energy sequence.^3,41 For further analyses, we have considered the partial density of states (PDOS) of these nanoalloys of different compositions as shown in Fig. 5(a–c). In addition, we have also plotted the DOS of undoped clusters in those figures for the better understanding of the band alignment of the alloyed systems. A deeper analysis reveals that, for the pure CdSe (black lines), the valence and conductance band edges are largely contributed from the Se-p and d orbitals, whereas at the extreme situation, when all the Se atoms are replaced by Te atoms, it is the Te atom whose p and d orbitals participate largely to the frontier bands of the nanoalloys (red lines). In the intermediate Te composition, it is the interplay between Se and Te atom to contribute to the frontier bands. Around 30% Te composition, it is very clear from the Fig. 5(a) that, valence band edge remains almost at the same position as that of the undoped CdSe, whereas conduction band edge is shifted towards the Fermi level and reaches a minimum. For the case of 50% doping, both the valence and conduction band edges are upshifted, but shifting in valence band edge is large compared to the conduction band edge, resulting a overall decrease in the band gap of the system. Further interesting fact we observe by increasing the dopant concentration is that, both the valence and conduction band edges are shifted up in comparison to those of undoped CdSe and ultimately they tend to the valence and conduction band edges of the undoped CdTe, respectively. As for the undoped CdSe and CdTe nanoclusters, the relative band alignment of the system is found to be type-II, where the band offset is large in valence band edge compared to the conduction band edge and hence by increasing the doping concentration of the Te atoms, the band gap of the alloyed system at first decreases, reaches to a minimum value and afterward increase. Thus, the bowing nature of the band gap variation of the CdSe_xTe_1−x nanoalloy as a function of doping concentration can be explained from their relative band alignments/from the above argument. So from the density of states analysis we find that the dopant atoms play an important role in controlling the luminescence properties of nanoalloy QDs. The results corroborate well with the previous experimental and theoretical results.^22,41,54

Fig. 3 Variation of band gap with the change of composition of the nanoalloys of different sizes. Here black, red, green, blue and magenta lines represent 56–56, 66–66, 87–87, 105–105, 117–117 cluster sizes, respectively.

Fig. 4 Variation of HOMO–LUMO energies as a function of composition of the (117–117) nanoalloy. Red and black lines represent HOMO and LUMO energy levels, respectively. The non linear nature of band gap energy with the change of composition is depicted here.

Fig. 5 Projected density of states (PDOS) of Cd₁₁₇Se₈₁Te₃₆ (a), Cd₁₁₇Se₅₇Te₆₀ (b) and Cd₁₁₇Se₃₃Te₈₄ (c) nanoalloys, respectively. Black and red lines show the DOS of pure Cd₁₁₇Se₁₁₇ and Cd₁₁₇Te₁₁₇ in all these pictures. PDOSs of CdSe and CdTe of Cd₁₁₇Se₈₁Te₃₆, Cd₁₁₇Se₅₇Te₆₀ and Cd₁₁₇Se₃₃Te₈₄ nanoalloys are shown with light green and blue lines in (a), magenta and orange in (b) and maroon and cyan in (c), respectively. Fermi energies are set at 0 eV for all the graphs.

Fig. 6 describes the charge density distribution of the band-edge states of different doped nanoalloy QD as well as undoped CdSe and CdTe QD. From the figure, we find that for both CdSe and CdTe undoped nanoclusters, the HOMO and LUMO states are not well separated (Fig. 6(a) and (e)). It is surprising to note that charge separation increases with the increase in percentage of doping and is the maximum at the 50% Te doped cluster where the band edge charge densities are localized to different parts of the nanoalloy. Such kind of size and impurity dependent carrier localization was also reported for CdTe/CdSe core/shell nanocrystals.²⁶ However, from the above fact it can be conclude that, by varying the Te concentration one can easily tune the band gap and also the charge separation in the HOMO and LUMO levels of the alloyed quantum dots. Such a localisation of band edge wavefunctions has been proved to be very crucial for solar energy harvesting process.^39,40 So, one may conclude that, Te doped CdSe nanoalloys, by virtue of their controllable optical properties and carrier dynamics are superior solar energy harvesting materials.

Fig. 6 (a–e) are the charge density plots of the HOMO (orange) and LUMO (blue) of the nanoalloys Cd₁₁₇Se₁₁₇, Cd₁₁₇Se₈₁Te₃₆, Cd₁₁₇Se₅₇Te₆₀, Cd₁₁₇Se₃₃Te₈₄, and Cd₁₁₇Te₁₁₇, respectively. Among all the figures, HOMO and LUMO charge densities are well separated in (c), i.e., for Cd₁₁₇Se₅₇Te₆₀ cluster. The isosurface value of 0.0001 e Å⁻³ is taken into account.

3.3. Mulliken population

An understanding of the surface charge of the nanoparticle is very crucial to study the dynamical processes occurring in these systems. To gain insight the surface charges of these nanoalloys, we perform Mulliken charge distribution analysis of the doped as well as undoped systems. Fig. 7 represents Mulliken populations for the individual atoms as a function of their radial distance for Te doped CdSe nanoalloys of different compositions. Here, it is worth to mention that only the valence electrons are considered for such analysis. From the figure it is clear that the magnitude of positive and negative charges on Cd and Se/Te atoms in the inner region of the quantum dots are almost same. In the inner region, all the atoms are fully coordinated, and there is about 0.40e charge transfer from Cd to Se, for both in case of undoped as well as doped CdSe nanoalloys. On the other hand, interestingly, when all the Se atoms are replaced by Te, the net charge transfer in the core region from Cd to Te becomes relatively low (0.36e) because of the more electropositive nature of Te in comparison to Se. However, the magnitudes of the charges on the Cd atoms in the surface region are not the same, and also the values for both atoms differ from those of the inner region. The surface Se atoms have less negative charges than the core Se atoms, because the coordination of the surface Se atoms is fulfilled by passivating with H atoms. As H atoms are less electropositive than Cd atoms, a lesser amount of charge is transferred to surface Se atoms as compared to bulk Se atoms. On the other hand, the surface Cd atoms have more positive charge than the core Cd atoms. This is so because the surface Cd atoms are fulfilling their coordination by forming a bond with O atoms of passivating –OH groups. Being more electronegative than Se, O atoms are abstracting more charge from surface Cd atoms making them more electropositive. There are two different types of H atoms present in the clusters, one attached to the Se atoms and others the H atoms of the passivated –OH groups, and accordingly they possess different Mulliken charges. The H atoms attached to the Se atoms have less positive charges as compared to H atoms of –OH groups. With increasing the degree of substitution of Se by Te, Te atom enters into the core region of the nanoalloys, and subsequently charge transfer takes place from Cd to Te instead of Se. Situating at the same radial position it is quite obvious that the Te atom will carry less amount of negative charge than Se. Another interesting phenomenon is also being reflected from the Mulliken charge distribution; a careful observation revels that with increasing the dopant concentration, the distribution of charge becomes more asymmetric of the individual atomic species in comparison to their mother QD. Furthermore, it is also found that this asymmetric charge distribution is maximum for the case of 50% dopant concentration (please see Fig. 7(g)), at that point the band gap variation it is minimum as a function dopant concentration. From the above fact, it can be conclude that the system with more symmetric charge distribution possess higher band gap value.

Fig. 7 Mulliken charge of the nanoalloys with different compositions. Black, blue, green, red and gray regions indicate the Mulliken population of charge for Cd, Se, Te, O and H atoms, respectively. Mulliken charges are distributed from centre of quantum dots to its surface.

4. Conclusion

In the present work, we have performed the theoretical calculations on the electronic structures, density of states, and Mulliken population analysis for the CdSe_1−xTe_x nanoalloys within a framework of SCC-DFTB method. The analysis of our calculations confirms that increasing Te content leads to significant reduction of the band gap of the doped nanoalloys and the 50% Te content composition shows a minimum band gap value of 2.45 eV. Furthermore, we also report that substituted nanoalloys have binding energies in between that of undoped CdSe and CdTe clusters, which ensures the formation of the alloyed clusters. From the density of states analysis we show that the dopant plays an important role in controlling the overall charge separation and hence luminescence properties of the nanoalloys. We also emphasize that one can enhance photo anode properties of the studied nanocrystals by maintaining surface area, and crystallite size and the level of doping. Hence, our study may serve as a quantitative theoretical prediction for such properties. We believe that this work may guide future engineering and design of the nanocrystals by manipulating of the electronic structures of these materials with different compositions to achieve more applications in the field of biological imaging and optoelectronic devices.

Acknowledgements

The authors sincerely acknowledge UGC, New Delhi, Govt. of India for partial financial support (Grant No. 43-174/2014(SR)). The financial support from SERB-DST, New Delhi through the project Ref. No. CS-085/2014 is gratefully acknowledged. A. P. sincerely acknowledges UGC Dr DS Kothari Fellowship, Govt. of India.

References

1. A. P. Alivisatos, Science, 1996, 271, 933.
2. C. B. Murray, C. Kagan and M. Bawendi, Annu. Rev. Mater. Sci., 2000, 30, 545–610.
3. G. I. Maikov, R. Vaxenburg, A. Sashchiuk and E. Lifshitz, ACS Nano, 2010, 4, 6547–6556.
4. M. L. Steigerwald and L. E. Brus, Acc. Chem. Res., 1990, 23, 183–188.
5. M. Brust, M. Walker, D. Bethell, D. J. Schiffrin and R. Whyman, J. Chem. Soc., Chem. Commun., 1994, 801–802.
6. M. L. Steigerwald and L. E. Brus, Annu. Rev. Mater. Sci., 1989, 19, 471–495.
7. M. Steigerwald, A. Alivisatos, J. Gibson, T. Harris, R. Kortan, A. Muller, A. Thayer, T. Duncan, D. Douglass and L. Brus, J. Am. Chem. Soc., 1988, 110, 3046–3050.
8. N. Piven, A. S. Susha, M. Döblinger and A. L. Rogach, J. Phys. Chem. C, 2008, 112, 15253–15259.
9. C. Murray, D. J. Norris and M. G. Bawendi, J. Am. Chem. Soc., 1993, 115, 8706–8715.
10. T. Vossmeyer, L. Katsikas, M. Giersig, I. Popovic, K. Diesner, A. Chemseddine, A. Eychmüller and H. Weller, J. Phys. Chem., 1994, 98, 7665–7673.
11. J. Nanda, S. Sapra, D. Sarma, N. Chandrasekharan and G. Hodes, Chem. Mater., 2000, 12, 1018–1024.
12. P. Sarkar and M. Springborg, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 235409.
13. P. Sarkar, M. Springborg and G. Seifert, Chem. Phys. Lett., 2005, 405, 103–107.
14. S. Sarkar, S. Pal and P. Sarkar, J. Mater. Chem., 2012, 22, 10716–10724.
15. A. Guzelian, U. Banin, A. Kadavanich, X. Peng and A. Alivisatos, Appl. Phys. Lett., 1996, 69, 1432–1434.
16. A. Guzelian, J. B. Katari, A. V. Kadavanich, U. Banin, K. Hamad, E. Juban, A. Alivisatos, R. Wolters, C. Arnold and J. Heath, J. Phys. Chem., 1996, 100, 7212–7219.
17. O. I. Micic, C. J. Curtis, K. M. Jones, J. R. Sprague and A. J. Nozik, J. Phys. Chem., 1994, 98, 4966–4969.
18. R. Ferrando, J. Jellinek and R. L. Johnston, Chem. Rev., 2008, 108, 845–910.
19. C. Wang, B. L. Wehrenberg, C. Y. Woo and P. Guyot-Sionnest, J. Phys. Chem. B, 2004, 108, 9027–9031.
20. N. Pradhan, D. Goorskey, J. Thessing and X. Peng, J. Am. Chem. Soc., 2005, 127, 17586–17587.
21. B. Dabbousi, J. Rodriguez-Viejo, F. V. Mikulec, J. Heine, H. Mattoussi, R. Ober, K. Jensen and M. Bawendi, J. Phys. Chem. B, 1997, 101, 9463–9475.
22. Z. Feng, P. Becla, L. Kim, S. Perkowitz, Y. Feng, H. Poon, K. Williams and G. Pitt, J. Cryst. Growth, 1994, 138, 239–243.
23. H. Han, Z. Liu, Z. Wang, J. Zhang, Z. Peng and S. Yuan, J. Phys. Chem. Solids, 1995, 56, 389–391.
24. T. Franzl, J. Müller, T. A. Klar, A. L. Rogach, J. Feldmann, D. V. Talapin and H. Weller, J. Phys. Chem. C, 2007, 111, 2974–2979.
25. D. J. Norris, A. L. Efros and S. C. Erwin, Science, 2008, 319, 1776–1779.
26. L. Zhang, Z. Lin, J.-W. Luo and A. Franceschetti, ACS Nano, 2012, 6, 8325–8334.
27. B. Goswami, S. Pal and P. Sarkar, J. Phys. Chem. C, 2008, 112, 11630–11636.
28. W. Zhang, G. Chen, J. Wang, B.-C. Ye and X. Zhong, Inorg. Chem., 2009, 48, 9723–9731.
29. C. Ghosh, S. Pal, P. Sarkar and T. Frauenheim, Appl. Phys. Lett., 2009, 94, 123105.
30. A. Ceylan, K. Jastrzembski and S. I. Shah, Metall. Mater. Trans. A, 2006, 37, 2033–2038.
31. P. Couchman and W. Jesser, Thermodynamic theory of size dependence of melting temperature in metals, 1977.
32. J. E. Bernard and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36, 3199.
33. P. Dagtepe, V. Chikan, J. Jasinski and V. J. Leppert, J. Phys. Chem. C, 2007, 111, 14977–14983.
34. W. C. Chan and S. Nie, Science, 1998, 281, 2016–2018.
35. M. Bruchez, M. Moronne, P. Gin, S. Weiss and A. P. Alivisatos, Science, 1998, 281, 2013–2016.
36. A. Zaban, O. Micic, B. Gregg and A. Nozik, Langmuir, 1998, 14, 3153–3156.
37. X. Cai, H. Mirafzal, K. Nguyen, V. Leppert and D. F. Kelley, J. Phys. Chem. C, 2012, 116, 8118–8127.
38. Z. Chen, J. Moore, G. Radtke, H. Sirringhaus and S. O'Brien, J. Am. Chem. Soc., 2007, 129, 15702–15709.
39. Z. Pan, K. Zhao, J. Wang, H. Zhang, Y. Feng and X. Zhong, ACS Nano, 2013, 7, 5215–5222.
40. R. Plass, S. Pelet, J. Krueger, M. Grätzel and U. Bach, J. Phys. Chem. B, 2002, 106, 7578–7580.
41. B. Hou, D. Parker, G. P. Kissling, J. A. Jones, D. Cherns and D. J. Fermín, J. Phys. Chem. C, 2013, 117, 6814–6820.
42. B. I. MacDonald, A. Martucci, S. Rubanov, S. E. Watkins, P. Mulvaney and J. J. Jasieniak, ACS Nano, 2012, 6, 5995–6004.
43. L. Liao, H. Zhang and X. Zhong, J. Lumin., 2011, 131, 322–327.
44. J. H. Bang and P. V. Kamat, ACS Nano, 2009, 3, 1467–1476.
45. D. Porezag, T. Frauenheim, T. Köhler, G. Seifert and R. Kaschner, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 12947.
46. M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260.
47. T. A. Niehaus, S. Suhai, F. Della Sala, P. Lugli, M. Elstner, G. Seifert and T. Frauenheim, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 085108.
48. G. Seifert, J. Phys. Chem. A, 2007, 111, 5609–5613.
49. B. Aradi, B. Hourahine and T. Frauenheim, J. Phys. Chem. A, 2007, 111, 5678–5684.
50. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
51. S. Sarkar, S. Pal, P. Sarkar, A. Rosa and T. Frauenheim, J. Chem. Theory Comput., 2011, 7, 2262–2276.
52. S. Sarkar, B. Rajbanshi and P. Sarkar, J. Appl. Phys., 2014, 116, 114303.
53. S. Sarkar, S. Saha, S. Pal and P. Sarkar, J. Phys. Chem. C, 2012, 116, 21601–21608.
54. X. Zhong, M. Han, Z. Dong, T. J. White and W. Knoll, J. Am. Chem. Soc., 2003, 125, 8589–8594.
55. S. Bell and S. Sen, J. Vac. Sci. Technol., A, 1985, 3, 112–115.
56. J. D. Bryan and D. R. Gamelin, Prog. Inorg. Chem., 2005, 54, 47–126.
57. A. H. Reshak, I. Kityk, R. Khenata and S. Auluck, J. Alloys Compd., 2011, 509, 6737–6750.

---