A comparative study of doping effects of V and Cr on a SrAlSi superconductor†
Abstract
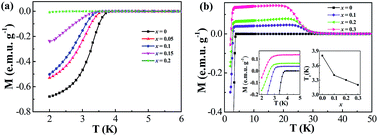
It is well known that the superconducting transition temperature (Tc) is very sensitive to the electronic density of states at the Fermi energy (N(EF)) and the Debye frequency (ΘD) for a BCS superconductor. However, which one plays a leading role in the ternary silicides AeMSi (Ae = Ca/Sr/Ba and M = Al/Ga) system is still unclear. Here, we report a comparative study of doping effects by V and Cr at Al sites in SrAlSi, which has a relatively high Tc among AeMSi systems. It is found that V and Cr atoms can be successfully introduced into SrAlSi with the actual solid solution limit up to 16 at% and 13 at%, respectively. In this case, the incorporation of V and Cr will have nearly identical effects in decreasing ΘD. Hall effect measurements demonstrate that V and Cr have dramatically different effects on the carrier concentration upon doping. In SrAl1−xVxSi, the carrier concentration is decreased by about three orders of magnitude and V dopants lead to the quenching of superconductivity at the highest doping level. In contrast, Cr almost does not change the carrier concentration, leading to a minor change in Tonsetc of 0.6 K. Our results provide solid evidence that the N(EF) should be responsible for the Tc in the transition metal doped AeMSi system.

 Please wait while we load your content...
Please wait while we load your content...