Explaining RANKL inhibition by OPG through quantum biochemistry computations and insights into peptide-design for the treatment of osteoporosis†
Abstract
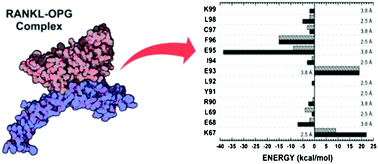
Osteoporosis is a degenerative disease associated with excessive bone resorption, a natural process performed by osteoclasts. In turn, osteoclast maturation is critically regulated by the receptor activator of nuclear factor kB ligand (RANKL), its signalling receptor (RANK), and its decoy receptor osteoprotegerin (OPG). The critical role of the protein triad, RANK–RANKL–OPG, in osteoclastogenesis has made their binding an important target for the rational development of drugs against osteoporosis. Based on this, we have performed a quantum biochemistry investigation of the binding between RANKL and its decoy receptor, OPG, in order to analyse the individual contributions of all amino acid residues involved in the complex formation, providing a deeper understanding of the inhibition process. The role of specific residues in the RANKL–OPG binding was evaluated through quantum biochemistry computations performed within the molecular fractionation with conjugate caps (MFCC) methodology, and inter-residue binding energies were calculated within the framework of density functional theory (DFT). Our simulations, considering water effects (implicit and explicit) and the role of the dielectric constant background, attested the major importance of site II, when compared to site I, over OPG binding and functionality, mainly through interactions performed by the tripeptide OPG core, I94–E95–F96. The obtained results also explain (i) the impact of a specific OPG mutation (F96L) on Paget's disease development; (ii) how some pioneers proposed that peptides efficiently inhibit the RANKL–OPG complex, acting as promising drugs for the treatment of osteoporosis. In conclusion, our quantum biochemistry approach provides a solid base that allows important insights into peptide and drug design for the treatment of osteoporosis based on RANKL–OPG binding inhibition.

 Please wait while we load your content...
Please wait while we load your content...