DFT study of Rh-decorated pristine, B-doped and vacancy defected graphene for hydrogen adsorption

Abstract

Rh adatom stability on graphene, with and without defects has been investigated by density functional theory (DFT) calculations to evaluate the feasibility to achieve a uniform dispersion of the metallic atom. Different defects introduced include B dopants, single vacancies and double 585 and 555-777 type vacancies. An energetic analysis of the hydrogen adsorption capacity for the different Rh decorated graphene structures was also performed. Dispersion force contribution to the adsorption energy was determined in order to obtain a quantitative method to know whether H₂ molecules adsorbed chemically or the adsorption on the Rh decorated graphene supports is controlled by van der Waals forces. Partial density of states (PDOS) for the different systems, were obtained to understand the Rh–C, H₂–Rh (adsorbed) and H–H interactions and magnetic effects, before and after Rh and H₂ adsorption. When H₂ molecules bind to Rh adatoms, an electrostatic interaction occurs due to a charge transfer from the metal to the graphene surfaces after adsorption. Bonding and Bader charge analysis are also included.

---

1. Introduction

The depletion of the non-renewable natural resources used for power generation and the pollution they produce caused the search for alternatives for energy production. The use of energy sources based on renewable resources constitutes an appropriate option to deal with this problem. A highly viable possibility is to replace fossil fuels with hydrogen based energy systems because they are a renewable resource, environmentally friendly and energy-efficient, making them a very promising energy carrier or fuel.^1,2 However, it is not naturally available as a ready to use substance, since uncompressed gas state hydrogen has a very low density and energy content.² Therefore, one of the challenges to be able to apply this material as fuel or energy carrier is to solve the technical problem of storage.

The most conventional candidates for hydrogen storage include liquid and gas hydrogen at high pressure. However, operational safety of the tanks and compressors limit the extent to which the gas can be pressurized.² For storage in liquid state, hydrogen liquefying process adds large amounts of power demand, making it not economically viable. For this reason, attention has been focused on porous carbon-based materials due to their chemical stability, low weight, high surface area and structure possible to be modified. These carbon-based adsorbents include carbon nanotubes (CNTs), carbon nanofibers (CNFs), activated carbon (AC), templated carbon (TC), graphene layers and fullerenes.^3–9 Since its first experimental synthesis in 2004 by Novoselov et al.,¹⁰ graphene has been applied in electrochemical and electrical storage: lithium batteries and supercapacitors,¹¹ and also hydrogen storage technology.^11,12

Unfortunately, at room temperature, hydrogen molecules adsorb physically on the carbon surface,^8,13,14 so the binding energy for hydrogen, lower than 0.1 eV per H₂,¹⁵ is less than the required value to achieve a reversible hydrogen adsorption–desorption at room conditions (0.16–0.4 eV per H₂).^16–18 A way to overcome this situation is by adding alkali, alkali earth^19–22 or transition metal (MT)^23–26 atoms. It has been demonstrated that alkali metal atoms cause a remarkable enhancement in the hydrogen adsorption capacity.^22,27,28 However, it appears that during the doping reaction the alkali atoms can block some carbon microporous adsorption sites, leading to a decrease in the specific surface area and in the maximum adsorption capacity observed at low temperature.²⁹ In addition, special caution needs to be taken to remove any moisture contamination during hydrogen storage measurement in alkali-doped carbon nanotubes or graphite, because moisture drastically increase the weight gain by reaction with (or adsorption on) the alkali species on carbon.³⁰

On the other hand, TM increases the binding ability of hydrogen by Kubas type interaction, due to empty d-orbitals.³¹ Studies on hydrogen adsorption on Ti decorated graphene or CNT^23,24 and on Pd decorated graphene²⁵ demonstrate the hybridization between the TM d orbital with H₂ σ orbitals, forming a Kubas complex.³² In principle, carbon-based materials decorated with light TMs, like Ti, Ni, Sc and V,^9,24,33–35 should be capable of binding multiple hydrogen molecules per metal atom, developing a binding energy between 0.2 and 0.6 eV and may satisfy the U.S. Department of Energy (DOE) goal. However, because the TM–TM interaction is much stronger than the TM-host materials, TM atoms tend to form clusters on the sheet surface decreasing dramatically the hydrogen storage capacity. To avoid it, a number of methods were attempted to enhance the metal binding, including modification of carbon surfaces by B and N doping or forming vacancies.^36–41 Beheshti et al.,³⁶ reported that graphene boron doping could prevent the clustering. Nachimuthu et al.,⁴⁰ found that Ni, Pd and Co atoms are suitable for decorating B-doped graphene surface, which can adsorbed stably on the surface. The effect of vacancy defects on metal atoms binding properties on graphene with hydrogen molecules was particularly investigated by Kim et al.³⁸ using first-principles calculations. They showed that a single vacancy defect enhance efficiently the metal binding and thus its dispersion. Lotfi et al.,³⁹ used density functional theory (DFT) to investigate the TM interaction (Sc, Ti and V) with 585 and 555-777 type double carbon vacancies, concluding that compared with pristine graphene, these defects improve TM binding significantly, which prevents clustering of TM over graphene. Also using DFT calculations, Ling Ma et al.⁴² studied the influence of B-doped and vacancy defects, while Zhou et al.⁴³ a combination of them, on the adsorption of hydrogen on Pd-decorated graphene.

DFT modeling of the hydrogen adsorption on heavy TM like Pd decorated graphene, with and without defects, and CNT has been amply studied.^{25,26,40–46} Instead, Rh decoration of carbon nanostructures for hydrogen storage has not yet been widely investigated. A recent work performed by Luna et al.,⁴⁷ analyzed the hydrogen adsorption on Rh decorating single-walled carbon nanotubes (SWCNTs). Other theoretical studies were performed on Rh/SWCNT^48–51 and Rh–graphene,^51–54 without including H₂ adsorption analysis. Previously, first-principles studies of hydrogen storage on Rh doped boron nitride (BN) sheets and nanotubes were performed,^55,56 showing that Rh atoms are capable of adsorbing up to three hydrogen molecules chemically. Also, the ability for hydrogen storage of Rh doped activated carbon compared with other metals was performed experimentally.⁵⁷

In this work we perform first-principles calculations using DFT to evaluate the stability of Rh on graphene with B dopants and various vacancy defects including single vacancy graphene (SVG), 585 and 555-777 types double vacancy graphene (585 DVG and 555-777 DVG), in order to prevent Rh aggregation. Results were compared with those obtained for Rh decorated pristine graphene. A hydrogen storage capacity analysis for the different systems was also performed. For all systems adsorption energies and electronic structures were calculated determining the type of interaction and mechanism involved between Rh adatom and graphene sheet (pristine and with defects) and among supported Rh and adsorbed hydrogen molecules.

2. Computational method

DFT calculations were performed using the Vienna Ab initio Simulation Package (VASP),^58–61 which employs a plane-wave basis set and a periodic supercell method. The generalized gradient corrected approximation (GGA) functional of Perdew, Burke, and Ernzerhof (PBE) was used.⁶² The Kohn–Sham equations were solved variationally using the projector-augmented-wave (PAW) method.^63,64 Spin polarization was considered in all calculations.

For the plane-wave basis set expansion a cutoff energy of 400 eV was used, overall with the gamma-centered Monkhorst–Pack scheme⁶⁵ with 4 × 4 × 1 k-points grid for the integration over the Brillouin zone. A Gaussian smearing approach was used for the electronic states partial occupations near the Fermi level, with a 0.2 eV smearing width.

Geometry optimizations were obtained by minimizing the total energy of the supercell using a conjugated gradient algorithm to relax ions,⁶⁶ until it converged within 10⁻⁴ eV and the forces on each ion were less than 0.02 eV Å⁻¹.

The Grimme's DFT-D2 method was adopted to account for the van der Waals interactions (vdW), which is optimized for several DFT functional.⁶⁷

Eqn (1) was employed to calculate the vacancy formation energy (E_f) for graphene with point defects,

where E_VG is the total energy of the SVG or DVG supercell, n_C is the number of carbon atoms of the defective graphene and μ_C, the chemical potential, is the energy per carbon atom in the optimized pristine graphene.

Eqn (2), was used to calculate the binding energy for an adatom (E_b) on the different supports considered,

E_b = E_G + E_Rh − E_Rh+G (2)

where E_G is the pristine or defected graphene total energy and E_Rh and E_Rh+G are the isolated Rh atom and the Rh-decorated pristine or defected graphene total energies, respectively. With this definition a positive binding energy corresponds to a stable adsorption on the graphene.

Adsorption energies of the nth H₂ molecule adsorbed on Rh-decorated graphene with B-doped and vacancy defects, up to the maximum capacity, were also calculated employing eqn (3).

E_ads(total) =  E_{Rh+G+(n−1)H2} + E_H2 − E_Rh+G+nH2 (3)

E_ads(total) is the total adsorption energy of the nth H₂ molecule, E_{Rh+G+(n−1)H2} and E_Rh+G+nH2 are the total energies of (n − 1) H₂ and nH₂ molecules adsorbed on Rh-decorated pristine, B-doped or vacancy defected graphene, respectively. E_H2 is the energy of the isolated H₂ molecule.

DFT-D2 method considers the total energy (E_total) as the sum of two terms shown in eqn (4),⁶⁷

E_total = E_KS + E_vdW (4)

where, E_KS and E_vdW are Kohn–Sham and van der Waal energies. Taking into account eqn (4), it is easy to also separate the adsorption energy into two contributions,⁶⁸ expressing the adsorption energy as the sum of the chemical adsorption energy and the dispersive adsorption energy,

E_ads(total) = E_ads-KS + E_ads-vdW (5a)

here E_ads(KS) and E_ads(vdW) are the adsorption energies calculated with Kohn–Sham energies, and with dispersion energies corresponding to van der Waals interactions. In this way, the nature of the bonding can be appreciated through the computed energies.

The graphene surface was built by cleaving the optimized graphite structure. Thus, the graphene unit cell consists of two carbon atoms with lattice parameters a = 2.46 Å. This value is in good agreement with the experimental value,⁶⁹ and other theoretical reports.^40,44 Then an hexagonal optimized 4 × 4 graphene supercell was used for the different systems analyzed, which corresponds to an in-plane lattice constant of 9.84 Å and a vacuum layer of 15 Å to avoid coupling between the adjacent layers. For the Rh/graphene, this setup corresponds to a coverage of one Rh adatom per 32 C atoms. According to other work,⁴² B-doped graphene was modeled by 4 B and 28 C atoms for the graphene sheet and SVG and DVG were built by removing one or two carbons atom from 4 × 4 hexagonal graphene supercell and geometrically optimizing the resulting structures. These last supports were decorated with a Rh adatom and relaxed again to obtain the most stable structures. Finally, the hydrogen adsorption on the different optimized Rh-decorated structures was studied.

In order to analyze the electronic structure, the electronic charges on atoms were computed using Bader analysis⁷⁰ and the atom projected density of states (PDOS) was obtained.

A qualitative study of the bonding between different atoms was also performed using the overlap population (OP) concept in extended structures (OPDOS),^71,72 and Bond Order (BO) as implemented in the DDEC6 method.^73–75

3. Results

3.1 Pristine, B-doped and vacancy defected graphene

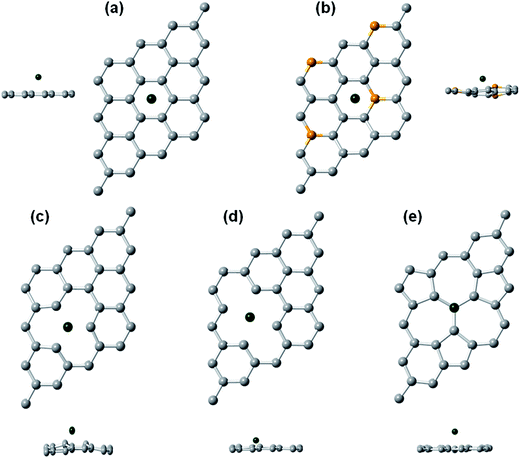
Fig. 1, shows the optimized support structures without Rh adatom. Pictures of pristine graphene were included, as a reference for a better view.

Fig. 1 (a) Pristine graphene, (b) B-doped graphene, (c) SVG, (d) 585 DVG, and (e) 555-777 DVG after geometry optimization. Grey and orange balls represent carbon and boron atoms, respectively.

In B-doped graphene, the C–C bond length remains practically unchanged (1.43 Å) with respect to pristine graphene (1.42 Å). While the C–B bond length, has a value of 1.46 Å.

SVG optimized geometry suffers Jahn–Teller distortion which leads to the saturation of two dangling bonds (C1 and C2 in Fig. 1(c)) toward the missing atom yielding to the formation of five-member and nine-member rings.⁷⁶ The bond length of the saturated dangling bonds (C1 and C2) decreases from 2.46 Å in the pristine graphene to 2.17 Å in the defected graphene, 3.5% larger than the value calculated by Zhou et al. (2.096 Å).⁴³ As a result, the vacancy other neighboring C atom (C3 in Fig. 1(c)) moves out of the graphene plane 0.29 Å, which has been observed in previous studies with values of 0.18–0.47 Å.^76,77 A magnetization in single vacancy graphene was also observed, as was suggested by Hjort et al.⁷⁸ The computed magnetization is 0.73 μ_B, which is lower than values reported by other authors (1.765 and 1.04 μ_B).^43,77 Taking into account that the magnetic moment for a single vacancy does not converge well for small slabs, due to defect–defect interaction,⁷⁷ our calculations were repeated for a 5 × 5 SVG (49 C atoms) slab, obtaining a magnetic moment larger than 1 μ_B. Relaxed DVG systems, are nonmagnetic which satisfies Lieb's theorem.⁷⁹ This result is not strange, since these last systems present reconstruction around the defect resulting in no dangling bonds, conforming structures of two pentagons and one octagon (585 structure, Fig. 1(d)) or three pentagons and three heptagons (555-777 structure, Fig. 1(e)) around the double vacancy defect instead of a hexagonal structure, like pristine graphene.⁸⁰

For the SVG and DVG, formation energies (E_f) were computed according to eqn (1), to examine the stability of vacancy defected graphene. Calculated E_f for SVG was of 7.8 eV, in good agreement with theoretical values from literature in the range 7.4–7.7 eV (ref. 76, 77 and 81) and compares well with the experimental value 7.5 ± 0.5 eV.⁸² In the case of double vacancy graphene values of 6.0 eV for 555-777 DVG and 8.2 eV for 585 DVG were obtained. These results are in good agreement with previous investigations^{44,80,83–85} where the difference lies in the use of a different supercell size, the approximation in the DFT treatment and the equation used to evaluate the E_f. According to the obtained results, the SVG can be more or less stable than the DVG, but in DVG, two C atoms are missing, so the energy per removed atom (3 eV and 4.1 eV) is much lower than SVG, being thermodynamically favored.⁸⁰

3.2 Rh decorated pristine, B-doped and vacancy defected graphene

In order to evaluate the stability of the different supports which will be used for hydrogen storage, the binding energy of a Rh adatom on graphene with B dopants and vacancy defects, considering SVG, 585 DVG and 555-777 DVG, was calculated. Rh adatom on pristine graphene was included for reference. For all graphene sheets a 4 × 4 supercell was employed, to keep the dopant and defect distribution and concentration, and to also fix the Rh coverage in a value that approximates the interaction of an isolated adatom with the graphene sheet. For all supports, different sites for the Rh adsorption were probed and energy was minimized, relaxing all the atoms and obtaining the most stable site for each system, which are shown in Fig. 2. A more significative distortion of the B-doped graphene and SVG surfaces after the Rh adsorption, can be appreciated in Fig. 2, side views.

Fig. 2 (a) Top and side view, of Rh-decorated pristine graphene, (b) B-doped graphene, (c) SVG, (d) 585 DVG, and (e) 555-777 DVG, after geometry optimization with Rh on the most stable site. Grey, orange and green balls represent carbon, boron and rhodium atoms, respectively.

In pristine and B-doped graphene the most stable adsorption sites are the hollow and BC₅ rings hollow sites respectively. The hollow site was also reported by other authors as the most stable site on graphene.⁵⁴ To the best of our knowledge, there is no data in the case of Rh adsorption on B-doped graphene, however Ma et al. found that Pd locates hollow sites.⁴² For graphene with vacancy defects our results indicate that on SVG and 585 DVG, Rh prefers to locate on the center of the defect, as reported for Pd atoms;^42,43 for 555-777 DVG, the Rh atom locates on top of the C atom belonging to the three heptagon rings, unlike Pd atoms which prefer the C–C bridge site common to two heptagonal rings.⁴²

Table 1, lists the binding energies for the Rh atom (E_b), adatom heights (z_C–Rh), sheet distortion (Δz) and magnetic moment (μ) for the Rh-decorated pristine, B-doped and vacancy defected graphene sheets. E_b was calculated using eqn (2), geometric parameters are defined as a previous work;⁸⁶ z_C–Rh is the difference between the adatom z coordinate (perpendicular to graphene layer) and the z coordinates average of the atoms in the graphene layer and Δz is computed as the maximum deviation in z direction of the atoms in the graphene layer from their average positions.

Table 1 Calculated binding energies, geometrical parameters and magnetic moment of Rh adatom over pristine graphene, B-doped graphene, SVG, 585 DVG and 555-777 DVG for the most stable site

System	Eb (eV)	zC–Rh (Å)	Δz (Å)	μ/μB
Pristine	1.96	1.81	0.02	0.74
B-Doped	3.95	1.35	0.47	0.00
SVG	8.37	1.50	0.41	0.00
585 DVG	7.44	0.84	0.13	0.76
555-777 DVG	3.29	1.79	0.16	0.00

---

The results for Rh adatom on pristine graphene are in good agreement with those reported by Manadé et al.⁵⁴ As expected; B dopants and vacancy defects improve the metal binding properties of the graphene sheet giving place to more stable structures. This effect was also reported with other transition metal atoms adsorbed on B-doped graphene,^37,40,42 and on graphene containing vacancies.^38,41–43 It is important to mention that since the Rh adatom binding energy on SVG and 585 DVG is larger than the experimental cohesive energy (5.75 eV) for Rh,⁸⁷ these defects are useful to avoid the formation of clusters and favor the metal atomic dispersion over the defects. Then the hydrogen storage capacity could be enhanced, because the amount of chemisorbed hydrogen molecules can be reduced by cluster formation.^55,88 Finally, in addition to the increase in the binding energy, for all considered defects the adatom distance to the surface is reduced with respect to the pristine graphene, and in some cases Δz reflects the distortion observed in Fig. 2.

3.3 Electronic structure of pristine and defected graphene sheets with a without Rh

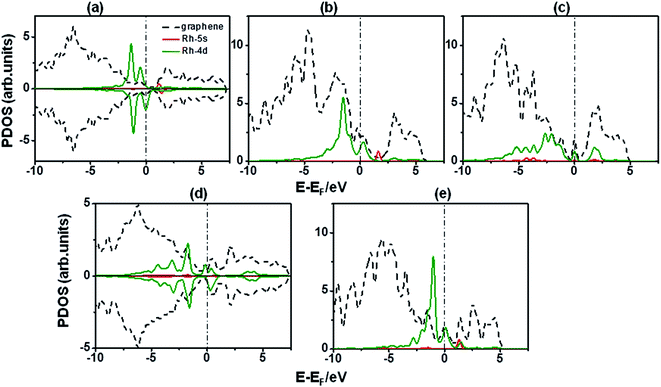
A study of the electronic structure was performed trying to understand in a better way the Rh binding on pristine, B-doped and vacancy defected graphene. Initially the total density of states (TDOS), and the partial density of states (PDOS) projected on s and p orbitals, on C and B atoms for the different supports without Rh adatoms was analyzed and are shown in the Fig. 3.

Fig. 3 Total density of states (TDOS) and partial density of states (PDOS) projected on C 2s and 2p orbitals of (a) pristine graphene, (b) B-doped graphene, (c) SVG, (d) 585 DVG, and (e) 555-777 DVG before the Rh adsorption.

The behavior observed for TDOS in Fig. 3(a)–(e) is very similar to those obtained by Ma et al.⁴² Fig. 3(a) shows that graphene presents a semiconductor character, which changes when it is doped with B, where the Fermi level shifts to the highest occupied molecular orbital (HOMO) level (Fig. 3(b)). This is due to the presence of p states provided by the introduction of B-dopants with the p_z orbital empty, which acts as a strong charge acceptor center, as shown in Fig. 3(a)–(b) PDOS curves. As previously mentioned, the SVG has a magnetic moment, this is mainly due to the asymmetry between up and down p states (see Fig. 3(c)). Similar to B-doped graphene, vacancy defected graphene sheets also show noticeable strong peaks near the Fermi level (see Fig. 3(c)–(e)). This means that there are electron deficient states, which can be associated mainly with p states (see PDOS Fig. 3(c)–(e)), giving to these structures the property to accept electrons coming from the adsorbate.⁴²

Fig. 4(a)–(e) show the PDOS on Rh atom and the graphene sheets for pristine, B-doped and vacancy defect after Rh decoration. In the case of Rh-adatom on pristine graphene the partially occupied 4d states of Rh extend approximately in the range of −6 to 0 eV below the Fermi level. d orbitals are not localized despite of the absence of defects on pristine graphene, indicating hybridization between Rh 4d orbital with C 2p orbitals which is stronger in the range −2 to 0 eV. It can also be observed that graphene states above the Fermi level decrease when compared with pristine graphene without Rh (Fig. 3(a)), meaning that Rh 4d orbitals not only interact with C π orbitals but also with C π* orbitals, probably due to a Dewar interaction^89,90 between graphene and Rh atom. This type of interaction was observed for Ti adsorption on pristine graphene as well.²³ In addition, the shift between spin up and down for the highest two peaks corresponding to Rh d states, and the fact that the spin up states are almost filled contrary to spin down states which are partially filled, make the system magnetize. So, Rh d electrons are the main contribution to the magnetization in this case with a lesser contribution of the C states. Compared to pristine graphene, B-doped and vacancy defected graphene 4d states are shifted toward higher energies offering more unfilled 4d states. It can be inferred that some electrons from the Rh atom are transferred to the B-doped or vacancy defected graphene sheet, filling the acceptor like states and leading to much stronger interaction between Rh adatom and the graphene sheets with defects.⁴²

Fig. 4 Partial density of states (PDOS) projected on Rh-5s orbitals, Rh-4d orbitals and on carbon (and boron) surface atoms for (a) pristine graphene, (b) B-doped graphene, (c) SVG, (d) 585 DVG, and (e) 555-777 DVG after the Rh adsorption.

Partially filled 4d orbitals of Rh adsorbed on B-doped graphene and 555-777 DVG (Fig. 4(b) and (e)), show a stronger hybridization than on pristine graphene, due to the 4d states which are distributed in a wide range below the Fermi energy instead of the more localized behavior observed on pristine graphene (Fig. 4(a)). This phenomena is more noticeable for the other defects, SVG and 585 DVG, where the 4d partially filled orbitals are spread over a much wider range from −8 to −1 eV, resulting in a stronger hybridization among Rh-4d orbitals and C π and π* orbitals (Fig. 4(c) and (d)). For these last cases, Rh-5s orbital changes from almost unfilled to occupied or partially filled orbital, presenting some 5s states below the Fermi level and no states above E_f, which means there is an electron backdonation from C 2p orbitals to Rh-5s orbital that contributes to the Rh bonding to SVG and 585 DVG.⁴²

Bader charges calculated for all the systems decorated with Rh, indicate that there is a transfer in the range of 0.38–0.73 e⁻ from Rh to the graphene surface with and without defects, confirming the behavior observed by the analysis of PDOS. This phenomenon leads to the creation of an electric field on the surface, due to the Rh positive charge and negatively charged graphene which form a dipole.²³

As mentioned before, the introduction of B atoms to dope graphene produces changes in the HOMO, and it is also expected that some changes occur with the introduction of other defects. For that reason, an analysis of the HOMO and the lowest unoccupied molecular orbital (LUMO), was performed for the different systems studied. In this sense, isosurfaces were built for these states before and after the Rh adsorption. Fig. 5 shows the results obtained.

Fig. 5 Isosurfaces for HOMO and LUMO states for (a) pristine graphene, (b) B-doped graphene, (c) SVG, (d) 555-777 DVG, and (e) 585 DVG before and after Rh adsorption.

Fig. 5(a), shows π and π* orbitals of graphene, corresponding to HOMO and LUMO states respectively. After Rh adsorption, due to the interaction between the Rh and C, π electron density corresponding to HOMO states accumulates in the C ring just below the metal. Also, some LUMO states disappear after Rh binding, as expected for a Dewar interaction type between Rh and graphene. The spherical symmetry of the Rh orbital for LUMO, is consistent with the observed Rh-s unoccupied states (Fig. 4(a)), instead for HOMO the presence of a d_z² type orbital can be observed. A similar behavior is observed for B-doped graphene (Fig. 5(b)), with an increment in the HOMO states in graphene nearby the Rh atom. Also, an important decrease in unoccupied π and π* orbitals states can be observed, for LUMO after the Rh adsorption. According to these results, it is again verified that a charge transfer occurs from Rh to the substrate. In the case of SVG (Fig. 5(c)), the electron density accumulates especially in the bond between C1 and C2 carbon atoms and around C3 atom from the vacancy (see Fig. 1(c)), because of Jahn–Teller distortion. Nevertheless, there are considerable unoccupied states near the Fermi level surrounding the vacancy making it available to accept electrons. After the Rh adsorption, LUMO states increase significantly, meaning that the interaction with Rh concentrates electrons around the SVG, where the bonding with Rh occurs, and the π orbitals of carbons C1 and C2 are modified due to the interaction with Rh-d_z² orbital. For DVG substrates, again we can observe different densities for LUMO and HOMO states that are concentrated near the defects. In the case of the 555-777 DVG (Fig. 5(d)), an unoccupied p_z type orbital was observed at the carbon atom shared by the three heptagons, which allow us to infer why this site is the most stable for Rh adsorption. The depletion of the electronic density in the pentagon and heptagon rings corresponding to HOMO after the Rh adsorption, reveals the interactions between Rh-d and C π orbitals. Finally, HOMO electronic densities for the 585-DVG (Fig. 5(e)), show the C–C bond breaking corresponding to the pentagons and the octagon and the formation of C–Rh bonds. At the same time, a decrease in unoccupied states around these C atoms and the appearance of Rh-d orbital can be observed in the LUMO state.

Charge distribution in the adsorption region is shown in Fig. 6. The charge density difference (Δρ) isosurface, is obtained as: Δρ = ρ_Rh–G − ρ_G − ρ_Rh. In this equation, ρ_Rh–G represents the charge density of the system formed by Rh adsorbed on the graphene surfaces with and without defects, while ρ_G and ρ_Rh indicate the charge density of the surfaces without Rh and the Rh atom without surface, respectively.

Fig. 6 Isosurfaces of the charge density differences for (a) Rh/pristine graphene, (b) Rh/B-doped graphene, (c) Rh/SVG, (d) Rh/555-777 DVG, and (e) Rh/585 DVG. The red and blue colors correspond to the charge depletion and accumulation regions respectively, for a value for the isosurfaces of 0.002 e Å⁻³.

An accumulation of charge in the region between the Rh and C atoms occurs, reflecting the bonding between Rh and the substrate. It can also be observed that in all cases the upper part of the Rh atom remains positive, which in addition to some electron accumulation regions in the substrate indicates charge transfer from Rh to substrate predicted before from Bader analysis.

3.4 Study of the H₂ adsorption on the Rh/pristine, Rh/B-doped, Rh/SV and Rh/DV graphene sheets

In this section, H₂ molecular adsorption properties are studied for the different Rh decorated structures. An H₂ molecule is located next to the Rh atom while the system is allowed to relax. Then another H₂ molecule is added and again a geometry optimization is done. The process is repeated until the maximum capacity of the system is reached. For each step, different initial geometries were employed to obtain the ground state.

Table 2, lists the adsorption energies of the nth H₂ molecules adsorbed on Rh-decorated pristine graphene, B-doped graphene and vacancy defected graphene, calculated with eqn. (3) and (5c), for the different supports. Geometrical parameters calculated for each case are also reported; d_Rh–H and d_H–H represent the distance between Rh and H atoms and the H₂ molecule bond length after being adsorbed for the last molecule added, and d_avg(Rh–H) and d_avg(H–H) are the average Rh–H distance and H–H bond length respectively, for all H₂ molecules adsorbed. Based on these results it can appreciated that for all the Rh-decorated supports the first molecule attaches to Rh atom chemically. As can be observed in Fig. 7, the first H₂ molecule conserves the geometry but d_H–H is in the range 0.79–0.96 Å yielding to a rather elongated bond with respect to the isolated molecule of H₂, for which a value of 0.75 Å was calculated.²⁵ The elongation observed when the H₂ molecule adsorbs on to Rh atom is in consonance with Kubas metal–dihydrogen complex in the range 0.8–0.9 Å), staying only slightly deviated from this values for Rh–pristine graphene and Rh–585 DVG. So it can be expected that a Kubas type interaction exists between Rh atom and H₂ molecule, where the H₂ σ and σ* molecular orbitals interact with the metal orbitals having an electron donation and backdonation process.

Table 2 Calculated adsorption energies and geometrical parameters of different number of H₂ molecules on pristine graphene, B-doped graphene, SVG, 585 DVG and 555-777 DVG, for the optimized structures

	H2 molecules	Eads(total) (eV)	Eads(vdW) (eV)	davg(Rh–H) (Å)	davg(H–H) (Å)	dRh–H (Å)	dH–H (Å)
H2/Rh/graphene	1H2	1.08	0.05	1.68	0.96	1.68	0.96
	2H2	0.48	0.10	1.71	0.92	1.71	0.91
	3H2	0.08	0.07	2.43	0.86	3.87	0.75
H2/Rh/B doped-graphene	1H2	0.86	0.09	1.74	0.88	1.74	0.88
	2H2	0.70	0.10	1.73	0.89	1.75	0.87
	3H2	0.08	0.10	2.27	0.84	3.35	0.75
H2/Rh/SVG	1H2	0.30	0.09	1.98	0.79	1.98	0.79
	2H2	0.24	0.11	2.04	0.78	2.03	0.79
	3H2	0.19	0.12	2.10	0.78	2.12	0.78
H2/Rh/585 DVG	1H2	0.19	0.09	1.93	0.82	1.93	0.82
	2H2	0.13	0.13	2.03	0.80	2.04	0.79
H2/Rh/555-777 DVG	1H2	0.89	0.05	1.75	0.88	1.75	0.88
	2H2	0.66	0.08	1.72	0.90	1.73	0.91
	3H2	0.09	0.08	2.23	0.84	3.21	0.76

---

Fig. 7 Optimized structure for the first H₂ molecule adsorbed on the (a) Rh/pristine graphene, (b) Rh/B-doped graphene, (c) Rh/SVG, (d) Rh/585 DVG, and (e) Rh/555-777 DVG.

Furthermore, d_Rh–H lies in the range 1.68–1.98 Å, which is also consistent with the distance in the Pd–H₂ Kubas complex (d_M–H = 1.67–2.05 Å) as cited in literature.³² Therefore, a single H₂ molecule is molecularly chemisorbed on the Rh atom and the interaction between Rh and H₂ in some cases is expected to be similar to a Kubas interaction. The fact that the first molecule is chemically adsorbed can also be observed in the small value of the E_ads(vdW) for all the Rh decorated supports. Based on the value of E_ads(vdW) we can estimate easily how many molecules can be adsorbed chemically for the different systems. For pristine graphene the addition of a third H₂ molecule yield to a E_ads(vdW) value almost equal to that obtained for E_ads(total), meaning that there is no chemical contribution to the binding and it is dominated by van der Waals forces. Instead, in the case of Rh decorated B-doped graphene, the E_ads(total) is smaller than E_ads(vdW) which means that, at the equilibrium adsorption distance, some repulsion occurs between the H₂ molecule and the surface atoms,⁶⁸ so the molecule remains attached only by dispersion interactions. In the same way, 555-777 DVG can adsorbe two molecules chemically, and Rh decorated 585 DVG can adsorb only one molecule chemically, where the second molecule adsorption on Rh adatom is dominated by dispersion forces. This is consistent with the Rh–H distance and H₂ bond lengths, which are approximately 2 Å or less and between 0.78 and 0.96 Å respectively for the chemically adsorbed molecules. When the H₂ molecule is adsorbed physically the Rh–H distance increases to 3.21–3.87 Å and H₂ bond length tends to a value close to the isolated H₂ molecule. Only the SVG Rh-decorated support can adsorb up to three molecules chemically. Comparing E_ads(total) and E_ads(vdW) it can be seen that there is a considerable chemical contribution even in the case of three H₂ molecules adsorbed.

In general the Rh–H distances are equal for the H₂ chemical adsorption on Rh–pristine, Rh–B-doped graphene and Rh–555-777 DVG, as expected in Kubas interaction, but the molecules adsorbed chemically on Rh–SV and Rh–DV-585 graphene show, in some cases, that each pair of Rh–H distances are slightly different, breaking the symmetry expected for a Kubas interaction. The calculation of Bader charges for H atoms in H₂ allow us to verify that one of the atoms has charge depletion and the other has a charge accumulation for each adsorbed H₂ molecule, meaning that the H₂ molecule polarizes. The interaction between the dipole formed on the surface and the H₂ dipole is the responsible for producing different Rh–H distances for each molecule. This effect was also observed by Ma et al.⁴² In addition, there is an electrostatic interaction that contributes to the adsorption energy in these cases. This phenomena was previously observed by Yoon et al.⁹¹ who showed an increase in the binding strength of molecular hydrogen on charged fullerenes, and was also observed on Ca decorated CNT.⁹²

Additional calculations were carried out to test the validity of the employed Grimme's method, with the more accurate vdW-DF2 method for some systems with one H₂ molecule.⁹³

The interactions between H₂ molecules and the supported Rh atom were analyzed using PDOS projected on Rh-s and Rh-d orbitals and on H₂-s states, for Rh/pristine graphene, Rh/B-doped graphene, Rh/SVG and Rh/555-777-DVG after the adsorption of one to three H₂ molecules. In Fig. 8(a) for one H₂ molecule, the system remains magnetized especially due to the contribution of Rh d electrons. Then, as more H₂ molecules are added, the magnetic moment disappears. The same thing occurs for the Rh–585 DVG system, which has a magnetic moment, as was mentioned in the previous section, but when only one H₂ molecule is adsorbed, the system magnetization is zero. Hybridization of the Rh-4d orbitals with H₂-σ orbitals between −9 and −7.5 eV is observed in all the cases, with the presence of a new Rh-4d orbitals peak centered below −8 eV. It can also be observed a small peak corresponding to the Rh-5s orbital, which overlaps with the H₂-σ orbital peak, so there is also a small contribution of the Rh-5s orbital, in the electron donation of the H₂-σ orbital to the Rh atom. On the other hand, there are some very small peaks corresponding to H₂-s states in the range of −2.5 to 0 eV for Rh–pristine graphene, Rh/B-doped graphene, Rh/585 DVG and Rh/555-777 DVG, and between −5 to −2.5 eV for Rh/SVG, that interact very weakly with the Rh-4d orbitals and less with the Rh-5s orbital. These H₂-s states bellow the Fermi energy correspond to the H₂-σ* orbitals, which participate in the backdonation process, confirming Kubas type interaction. The increment in the number of molecules, increases the number of states corresponding to this type of interaction, which can be better visualized when a second H₂ molecule is added. Also in this case, a second H₂-s peak can be visualized around −8 and −7.5 eV that overlaps with other Rh-4d orbitals peak, which is probably related with the hybridization between H₂-σ orbital with the d_xz and d_yz orbitals. In this case, the first peak at more negative energies (centered among −8.75 and −8.25 eV) corresponds to the d_z² orbital, as was described for H₂ and Ti/graphene interaction.²³ In the H₂ adsorption on Rh/SVG, the antibonding H₂-s states, shift to lower energies and seem to be more hybridized with Rh-5s states instead of Rh-4d sates, probably being a lesser effect of electron backdonation. This explains the fact that the distance between the H₂ molecule and the Rh atom is in the order of 1.9–2.1 Å, and d_H–H in the order of 0.78–0.79 Å, with a weaker chemical interaction. But, in contrast to the other systems, SV is the only Rh decorated support that can adsorb with an appreciable chemical contribution up to three molecules, as we mention before. This is not the case for the addition of a third molecule for Rh/pristine graphene, Rh/B-doped graphene and Rh/555-777 DVG, which exhibit an new peak between of the H₂-s states in the range −6 to −5 eV that does not interact with any metal orbital, indicating that the third molecule is only binding with the Rh atom by van der Waals forces, as was concluded before, from the energetic point of view.

Fig. 8 PDOS projected on Rh-5s orbitals, Rh-4d orbitals and on H₂-s states for (a) Rh/pristine graphene, (b) Rh/B-doped graphene, (c) Rh/SVG, and (d) Rh/555-777 DVG after the H₂ adsorption, for one to three H₂ molecules.

As described for the other Rh-decorated supports the first H₂ molecule is adsorbed chemically on Rh/585 DVG. This behavior is observed in Fig. 9(a). The addition of a second H₂ molecule leads to a physical adsorption, which seems to contradict the PDOS observed in Fig. 9(b), in which the hybridization of Rh s and Rh d orbitals with H₂-σ orbital is observed. But this is not the case if the adsorption energy for all the molecules, is calculated employing E_ads(total) =  E_Rh+G + nE_H2 − E_Rh+G+nH2, where E_Rh+G+nH2 is the energy of the Rh-decorated graphene with nH₂ molecules adsorbed. Separating the Kohn–Sham and van der Waals terms in this equation, a value of 0.32 eV for E_ads(total) and 0.22 eV for E_ads(vdW) is obtained, so there is a chemical bond contribution, but it is dominated by van der Waals forces. This small chemical contribution explains the fact that the d_Rh–H have a value of 2.04 Å and d_H–H is 0.79 Å for the second H₂ molecule, instead of the higher values observed for the third molecule on Rh/pristine graphene, Rh/B-doped graphene and Rh/555-777 DVG, which is almost pure physically adsorbed.

Fig. 9 PDOS projected on Rh-5s orbitals, Rh-4d orbitals and on H₂-s states for Rh/585 DVG after the H₂ adsorption for (a) one H₂, and (b) two H₂.

In Table 3, Bader charges for the different amounts of H₂ molecules after the adsorption are reported. A negative value in almost all cases is observed, which means that the H₂ molecule receives electrons because of the electron backdonation process. In addition, values of approximately zero correspond to the cases where the electron donation and backdonation are compensated or the case where there only exists a physical interaction through dispersion forces.

Table 3 Bader charges relative to electron valence, for the adsorption of H₂ on Rh/pristine graphene, Rh/B-doped graphene, Rh/SVG, Rh/585 DVG and Rh/555-777 DVG, for the optimized structures

System	1H2	2H2	3H2
1H2/Rh/graphene	−0.118	—	—
2H2/Rh/graphene	−0.066	−0.065	—
3H2/Rh/graphene	−0.064	−0.065	0.001
1H2/Rh/B-doped graphene	−0.041	—	—
2H2/Rh/B-doped graphene	−0.032	−0.024	—
3H2/Rh/B-doped graphene	−0.024	−0.024	−0.007
1H2/Rh/SVG	−0.043	—	—
2H2/Rh/SVG	−0.001	−0.001	—
3H2/Rh/SVG	0.007	0.009	0.005
1H2/Rh/585 DVG	−0.011	—	—
2H2/Rh/585 DVG	−0.002	0.000	—
1H2/Rh/555-777 DVG	−0.063	—	—
2H2/Rh/555-777 DVG	−0.031	−0.066	—
3H2/Rh/555-777 DVG	−0.027	−0.041	−0.013

---

Fig. 10, shows a summary of the optimized systems for its maximum amount of adsorbed H₂ molecules. In order to obtain a better understanding of the different stages of the metal and hydrogen adsorption on graphene, bond order (BO) per atom and overlap population (OP) calculations were carried out for the SVG support, which contains the maximum number of adsorbed molecules when it is decorated with Rh. The analysis was performed for one to three molecules adsorbed, and the more relevant results for the atoms taken as reference indicated in Fig. 11, are listed in the Tables 4 and 5.

Fig. 10 Geometry of the optimized structure for the maximum capacity of H₂ molecule adsorbed on the (a) Rh/pristine graphene, (b) Rh/B-doped graphene, (c) Rh/SVG, (d) Rh/585 DVG, and (e) Rh/555-777 DVG.

Fig. 11 Selected atoms for bond order and overlap population analysis, (a) top, and (b) side view.

Table 4 Overlap population for selected pairs of atoms for the SVG, Rh/SVG, H₂ isolate molecule and H₂/Rh/SVG, for one to three H₂ molecules, optimized structures

Atoms	Distance/Å	Overlap population (OP)
		SVG	Rh/SVG	H2 free	1H2/Rh/SVG	2H2/Rh/SVG	3H2/Rh/SVG
C1–C2	1.40	0.893	0.856	—	0.851	0.851	0.851
Rh–C1	1.91	—	0.651	—	0.645	0.641	0.646
Rh–H	2.08	—	—	—	0.220	0.190	0.152
H–Hfree	0.75	—	—	0.551	—	—	—
H–Hmolecule1	0.79	—	—	—	0.432	0.438	0.446
H–Hmolecule2	0.79	—	—	—	—	0.436	0.446
H–Hmolecule3	0.78	—	—	—	—	—	0.449
Hmolecule1–Hmolecule2	3.16	—	—	—	—	0.013	0.011
Hmolecule1–Hmolecule3	3.32	—	—	—	—	—	0.016
Hmolecule2–Hmolecule3	3.31	—	—	—	—	—	0.015

---

Table 5 Bond order per atom for selected atoms for the SVG, Rh/SVG, H₂ isolate molecule and H₂/Rh/SVG, for one to three H₂ molecules, optimized structures

Atom	Bond order (BO) per atom
	SVG	Rh/SVG	H2 free	1H2/Rh/SVG	2H2/Rh/SVG	3H2/Rh/SVG
Cclose	3.43	4.05	—	4.05	4.06	4.08
Cfar	3.95	3.99	—	3.99	3.99	3.99
Rh	—	3.41	—	3.83	4.12	4.28
H (H2 free)	—	—	1.00	—	—	—
Hmolecule1	—	—	—	0.87	0.86	0.85
Hmolecule2	—	—	—	—	0.86	0.85
Hmolecule3	—	—	—	—	—	0.85

---

The bonding between the Rh and the graphene surface at the C vacancy region decreases the C–C OP from 0.893 to 0.856 (see Table 4). This is about 4% per bond, so since there are six C–C pairs first neighbor to the metal atom, it means a total decrease of 24%. At the same time, three Rh–C1 bonds are formed. When the H₂ molecules reach the surface, they interact with the Rh atom, forming a Rh–H bond at 2.08 Å for the first H₂ molecule with an OP of 0.220. The subsequent Rh–H OPs for the second and third H₂ molecules are 0.190 and 0.152, respectively. These OPs values indicate that the interaction is stronger with the first H₂ molecule. At the same time, the Rh–C OPs decrease about 1% with the first H₂ molecule and remains practically unchanged after the second and third H₂ adsorption. The H₂ bond length increases about 5% in all cases while its H–H OP decreases about 22%. The interactions between different H₂ pairs are poor, corresponding to an OP below to 0.02, and was evaluated for other pairs of hydrogen atoms with an OP less than 0.001 (not showed in the table).

Table 5 shows the evolution of BO during the adsorption process. For the graphene surface, the C atom close to the vacancy region (C_close) presents a value of 3.43 which is lower than the corresponding value for the carbon far for the adsorption site of Rh atom (C_far) of 3.95. After Rh adsorption, the BO in the C_close increases to 4.05. Subsequent H₂ adsorptions do no present any significant change in C BO. The BO for the Rh atom increases from 3.41 to 3.89, 4.12 and 4.28 when H₂ molecules are considered, while the H BO decreases from 1 in the free molecule to 0.87–0.85 in the adsorbed state, as a result of the antibonding electrons participating in the electron backdonation process. Furthermore, in the successive H₂ molecules adsorption, the molecules conserve practically the same bond order and overlap population, meaning that the chemical mechanism does not change during the successive adsorption verifying again that the change in the adsorption energy is due to van der Waals interaction (see E_ads(vdW) Table 2).

Based on the analysis of this section, the graphene with SV defect is the best choice for hydrogen storage purpose, because it not only helps to stabilize the dispersion of individual Rh atoms but also presents a H₂-molecular adsorption between the physisorbed and chemisorbed states, avoiding the hydrogen dissociation, and with a storage capacity superior to the other systems (3H₂-molecules per Rh atom). The adsorption energies are also in the range 0.19–0.3 eV, typical for a physicochemical interaction and it satisfies the requirement for easy adsorption and desorption of hydrogen under room conditions.^16–18

4. Conclusions

In this work, DFT calculations have been carried out to investigate the stability of Rh atoms adsorbed on pristine graphene, B-doped graphene and with different vacancy defects (SVG, 555-777 DVG and 585 DVG). In addition, hydrogen storage capacity for the different Rh decorated systems was evaluated. Based on binding energies calculated, we can affirm that a good Rh dispersion can be obtained on SVG and 585 DVG, preventing clustering due to the fact that Rh cohesive energy is lower than the binding energies for these defects. Rh atom decorated pristine, B-doped graphene, SVG and 555-777 DVG is capable of adsorbing up to three H₂ molecules, whereas Rh decorated 585 DVG can only adsorb up to two H₂ molecules. The first H₂ molecule is adsorbed chemically on Rh decorated graphene and partially dissociates. When a second molecule is adsorbed, a Kubas type interaction is observed in which the H–H bond is stretched. This interaction dominates the hydrogen adsorption when one or two molecules are chemisorbed on Rh decorated B-doped graphene and 555-777 DVG. In the case of Rh decorated 585 DVG, just one molecule can be adsorbed chemically, while the second molecule adsorption on Rh adatom is dominated by dispersion forces. Also for Rh adatom on pristine graphene, B-doped graphene and 555-777 DVG, the third H₂ molecule is absorbed by small van der Waals forces. Only SVG decorated with Rh, is able to adsorbed up to three molecules chemically, with a lower stretching of H₂ the molecules bond, and energies in the range of 0.19–0.3 eV, which are suitable for a H₂ adsorption–desorption at room conditions. The Rh-4d and Rh-5s orbitals hybridization with the H₂ σ orbital is the main mechanism for the H₂ adsorption, but there is also a contribution of the electrostatic interaction between surface dipole and polarized H₂. Magnetization of Rh decorated graphene and 585 DVG was observed due to the differences in Rh 4d up and down states, but disappears after the hydrogen adsorption. The use of Grimme or vdW-DF2 method show the same tendency in chemisorption results for one H₂ molecule.

Acknowledgements

We acknowledge the financial support given by SGCyT-UNS, CONICET – PIP 2014-2016: GI11220130100436CO and PICT-2014-1351. All authors are members of CONICET. We kindly acknowledge useful discussions with Prof. Ricardo Faccio and Dr Pablo Bechthold and suggestions from the reviewers.

References

1. R. A. Patricio, A. D. Sales, E. M. Sacramento, L. C. de Lima and T. N. Veziroglu, Wind Hydrogen Energy System and the Gradual Replacement of Natural Gas in the State of Ceará-Brazil, Int. J. Hydrogen Energy, 2012, 37, 7355.
2. K. Mazloomi and C. Gomes, Hydrogen as an Energy Carrier: Prospect and Challenges, Renewable Sustainable Energy Rev., 2012, 16, 3024.
3. L. Zubizarreta, A. Arenillas and J. J. Pis, Carbon Materials for H₂ Storage, Int. J. Hydrogen Energy, 2009, 34, 4575.
4. H. Jin, Y. S. Lee and I. Hong, Hydrogen Adsorption Characteristics of Activated Carbon, Catal. Today, 2007, 120, 399.
5. L. Wang and R. T. Yang, Hydrogen Storage on Carbon-Based Adsorbents and Storage at Ambient Temperature by Hydrogen Spillover, Catal. Rev.: Sci. Eng., 2010, 52, 411.
6. S. Hynek, W. Fuller and J. Bentley, Hydrogen Storage by Carbon Sorption, Int. J. Hydrogen Energy, 1997, 22, 601.
7. A. W. C. van den Berg and C. O. Areán, Materials for Hydrogen Storage: Current Research Trends and Perspectives, Chem. Commun., 2008, 6, 668.
8. Y. Yurum, A. Taralp and T. N. Veziroglu, Storage of Hydrogen in Nanostructured Carbon Materials, Int. J. Hydrogen Energy, 2009, 34, 3784.
9. Y. F. Zhao, Y. H. Kim, A. C. Dillon, M. J. Heben and S. B. Zhang, Hydrogen Storage in Novel Organometallic Buckyballs, Phys. Rev. Lett., 2005, 94, 155504.
10. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Electric Field Effect in Atomically Thin Carbon Films, Science, 2004, 306, 666.
11. M. Pumera, Graphene-based Nanomaterials for Energy Storage, Energy Environ. Sci., 2011, 4, 668.
12. A. J. Ferre-Vilaplana, Numerical Treatment Discussion and Ab Initio Computational Reinvestigation of Physisorption of Molecular Hydrogen on Graphene, Chem. Phys., 2005, 122, 104709.
13. B. Panella, M. Hirscher and S. Roth, Hydrogen Adsorption in Different Carbon Nanostructures, Carbon, 2005, 43, 2209.
14. R. Ströbel, J. Garche, P. T. Moseley, L. Jörissen and G. Wolf, Hydrogen Storage by Carbon Materials, J. Power Sources, 2006, 159, 781.
15. D. Henwood and J. D. Carey, Ab Initio Investigation of Molecular Hydrogen Physisorption on Graphene and Carbon Nanotubes, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 245413.
16. R. C. Lochan and M. Head-Gordon, Computational Studies of Molecular Hydrogen Binding Affinities: The Role of Dispersion Forces, Electrostatics, and Orbital Interactions, Phys. Chem. Chem. Phys., 2006, 8, 1357.
17. S. K. Bathia and A. L. Myers, Optimum Conditions for Adsorptive Storage, Langmuir, 2006, 22, 1688.
18. Y. H. Kim, Y. Zhao, A. Williamson, M. J. Heben and S. B. Zhang, Nondissociative Adsorption of H₂ Molecules in Light-Element-Doped Fullerenes, Phys. Rev. Lett., 2006, 96, 016102.
19. C. Ataca, E. Aktürk, S. Ciraci and H. Ustunel, High-capacity Hydrogen Storage by Metallized Graphene, Appl. Phys. Lett., 2008, 93, 043123.
20. C. Ataca, E. Aktürk and S. Ciraci, Hydrogen Storage of Calcium Atoms Adsorbed on Graphene: First-principles Plane Wave Calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 041406.
21. M. Yoon, S. Yang, C. Hicke, E. Wang, D. Geohegan and Z. Zhang, Calcium as the Superior Coating Metal in Functionalization of Carbon Fullerenes for High-capacity Hydrogen Storage, Phys. Rev. Lett., 2008, 100, 206806.
22. K. R. S. Chandrakumar and S. K. Ghosh, Alkali-metal-induced Enhancement of Hydrogen Adsorption in C₆₀ Fullerene: An Ab Initio Study, Nano Lett., 2008, 8, 13.
23. Y. L. Liu, L. Ren, Y. He and H. P. Cheng, Titanium-decorated Graphene for High-capacity Hydrogen Storage Studied by Density Functional Simulations, J. Phys.: Condens. Matter, 2010, 22, 445301.
24. T. Yildirim and S. Ciraci, Titanium-decorated Carbon Nanotubes as a Potential High-capacity Hydrogen Storage Medium, Phys. Rev. Lett., 2005, 94, 175501.
25. I. López-Corral, E. Germán, A. Juan, M. A. Volpe and G. P. Brizuela, DFT Study of Hydrogen Adsorption on Palladium Decorated Graphene, J. Phys. Chem. C, 2011, 115, 4315.
26. H. Xiao, S. H. Li and J. X. Cao, First-principles Study of Pd-decorated Carbon Nanotube for Hydrogen Storage, Chem. Phys. Lett., 2009, 483, 111.
27. K. Srinivasu, K. R. S. Chandrakumar and S. K. Ghosh, Quantum Chemical Studies on Hydrogen Adsorption in Carbon-based Model Systems: Role of Charged Surface and the Electronic Induction Effect, Phys. Chem. Chem. Phys., 2008, 10, 5832.
28. K. Srinivasu, K. R. S. Chandrakumar and S. K. Ghosh, Computational Investigation of Hydrogen Adsorption by Alkali-metal-doped Organic Molecules: Role of Aromaticity, ChemPhysChem, 2009, 10, 427.
29. S. Łoś, M. Letellier, P. Azaïs and L. J. Duclaux, Li Doped Carbons (Activated Microporous Carbons and Graphite): Characterization by Resonance Spectroscopies (ESR and Li NMR) and their Potentiality for Hydrogen Adsorption, Phys. Chem. Solids, 2006, 67, 1182.
30. R. T. Yang, Carbon, 2000, 38, 623.
31. G. J. Kubas, Fundamentals of H₂ Binding and Reactivity on Transition Metals Underlying Hydrogenase Function and H₂ Production and Storage, Chem. Rev., 2007, 107, 4152.
32. G. J. Kubas, Metal–dihydrogen and σ-bond Coordination: the Consummate Extension of the Dewar–Chatt–Duncanson Model for Metal–olefin π Bonding, J. Organomet. Chem., 2001, 635, 37.
33. J. W. Lee, H. S. Kim, J. Y. Lee and J. K. Kang, Hydrogen Storage and Desorption Properties of Ni-dispersed Carbon Nanotubes, Appl. Phys. Lett., 2006, 88, 143126.
34. T. Yildirim, J. Íñiguez and S. Ciraci, Molecular and Dissociative Adsorption of Multiple Hydrogen Molecules on Transition Metal Decorated C₆₀, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 153403.
35. E. Durgun, S. Ciraci and T. Yildirim, Functionalization of Carbon-based Nanostructures with Light Transition-metal Atoms for Hydrogen Storage, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 085405.
36. E. Beheshti, A. Nojeh and P. Servati, A First-principles Study of Calcium-decorated, Boron-doped Graphene for High Capacity Hydrogen Storage, Carbon, 2011, 49, 1561.
37. G. Kim and S. H. Jhi, Optimization of Metal Dispersion in Doped Graphitic Materials for Hydrogen Storage, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 085408.
38. G. Kim, S. H. Jhi, S. Lim and N. Park, Effect of Vacancy Defects in Graphene on Metal Anchoring and Hydrogen Adsorption, Appl. Phys. Lett., 2009, 94, 173102.
39. R. Lotfi and Y. Saboohi, A Comparative Study on Hydrogen Interaction with Defective Graphene Structures Doped by Transition Metals, Phys. E, 2014, 60, 104.
40. S. Nachimuthu, P. J. Lai and J. C. Jiang, Efficient Hydrogen Storage in Boron Doped Graphene Decorated by Transition Metals – A First-principles Study, Carbon, 2014, 73, 132.
41. K. M. Fair, X. Y. Cui, L. Li, C. C. Shieh, R. K. Zheng, Z. W. Liu, B. Delley, M. J. Ford, S. P. Ringer and C. Stampfl, Hydrogen Adsorption Capacity of Adatoms on Double Carbon Vacancies of Graphene: A Trend Study from First Principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 014102.
42. L. Ma, J. M. Zhang, K. W. Xu and V. Ji, Hydrogen Adsorption and Storage on Palladium-decorated Graphene with Boron Dopants and Vacancy Defects: A First-principles Study, Phys. E, 2015, 66, 40.
43. Q. Zhou, C. Wang, Z. Fu, L. Yuan, X. Yang, Y. Tang and H. Zhang, Hydrogen Adsorption on Palladium Anchored Defected Graphene with B-doping: A Theoretical Study, Int. J. Hydrogen Energy, 2015, 40, 2473.
44. D. Sen, R. Thapa and K. K. Chattopadhyay, Small Pd Cluster Adsorbed Double Vacancy Defect Graphene Sheet for Hydrogen Storage: A First-principles Study, Int. J. Hydrogen Energy, 2013, 38, 3041.
45. L. Ma, J. M. Zhang and K. W. Xu, Hydrogen Storage on Nitrogen Induced Defects in Galladium-decorated Graphene : A First-principles Study, Appl. Surf. Sci., 2014, 292, 921.
46. C. M. Ramos-Castillo, J. U. Reveles, R. R. Zope and R. de Coss, Palladium Clusters Supported on Graphene Monovacancies for Hydrogen Storage, J. Phys. Chem. C, 2015, 119, 8402.
47. C. R. Luna, V. Verdinelli, E. Germán, H. Seitz, M. A. Volpe, C. Pistonesi and P. V. Jasen, Hydrogen Adsorption and Associated Electronic and Magnetic Properties of Rh-Decorated (8,0) Carbon Nanotubes Using Density Functional Theory, J. Phys. Chem. C, 2015, 119, 13238.
48. J. X. Zhao and Y. H. Ding, Theoretical Study of the Interactions of Carbon Monoxide with Rh-decorated (8,0) Single-walled Carbon Nanotubes, Mater. Chem. Phys., 2008, 110, 411.
49. P. F. Yang, J. M. Hu, B. T. Teng, F. M. Wu and S. Y. Jiang, Density Functional Study of Rhodium Adsorption on Single-wall Carbon Nanotubes, Acta Phys. Sin., 2009, 58, 3331.
50. P. F. Yang, F. M. Wu, B. T. Teng, S. Liu and J. Z. Jiang, Structural, Curvature and Electronic Properties of Rh Adsorption on Armchair Single-walled Carbon Nanotube, Chin. Phys. B, 2010, 19, 097104.
51. I. Suarez-Martinez, C. P. Ewels, X. Ke, G. Van Tendeloo, S. Thiess, W. Drube, A. Felten, J.-J. Pireaux, J. Ghijsen and C. Bittencourt, Study of the Interface between Rhodium and Carbon Nanotubes, ACS Nano, 2010, 4, 1680.
52. V. Zólyomi, Á. Rusznyák, J. Kürti and C. J. Lambert, First Principles Study of the Binding of 4d and 5d Transition Metals to Graphene, J. Phys. Chem. C, 2010, 114, 18548.
53. K. Nakada and A. Ishii, Migration of Adatom Adsorption on Graphene Using DFT Calculation, Solid State Commun., 2011, 151, 13.
54. M. Manadé, F. Viñes and F. Illas, Transition Metal Adatoms on Graphene: A Systematic Density Functional Study, Carbon, 2015, 95, 525.
55. N. S. Venkataramanan, M. Khazaei, R. Sahara and H. Mizuseki, First-principles Study of Hydrogen Storage over Ni and Rh Doped BN Sheets, Chem. Phys., 2009, 359, 173.
56. L. P. Zhang, P. Wu and M. B. Sullivan, Hydrogen Adsorption on Rh, Ni, and Pd Functionalized Single-Walled Boron Nitride Nanotubes, J. Phys. Chem. C, 2011, 115, 4289.
57. I. Rossetti, G. Ramis, A. Gallo and A. Di Michele, Hydrogen Storage over Metal-Doped Activated Carbon, Int. J. Hydrogen Energy, 2015, 40, 7609.
58. G. Kresse and J. Hafner, Ab Initio Molecular Dynamics for Open-Shell Transition Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115.
59. G. Kresse and J. Hafner, Ab Initio Molecular-Dynamics Simulation of the Liquid-Metal-Amorphous-Semiconductor Transition in Germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251.
60. G. Kresse and J. Furthmüller, Efficiency of Ab Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6, 15.
61. G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
62. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865.
63. P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
64. G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave-Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
65. H. J. Monkhorst and J. D. Pack, Special Points for Brillouin-Zone Integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188.
66. W. H. Press, B. P. Flannery, S. A. Teukolsky and W. T. Vetterling, Numerical Recipies, Cambridge University Press, New York, 1986.
67. S. Grimme, Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction, J. Comput. Chem., 2006, 27, 1787.
68. R. E. Ambrusi, S. G. García and M. E. Pronsato, Formation of Ag Nanowires on Graphite Stepped Surfaces. A DFT Study, Appl. Surf. Sci., 2015, 324, 710.
69. J. Cervenka and C. F. J. Flipse, The Role of Defects on the Electronic Structure of a Graphite Surface, J. Phys.: Conf. Ser., 2007, 61, 190.
70. R. F. W. Bader, Atoms in Molecules – A Quantum Theory, Oxford University Press, Oxford, 1990.
71. R. J. Hoffmann, Solids and Surfaces: A Chemist's View of Bonding in Extended Structures, VCH, New York, 1988.
72. R. Dronskowski, Computational Chemistry of Solid State Materials: A Guide for Materials Scientists, Chemists, Physicists and others, Wiley-VCH, Weinheim, 2005.
73. N. Gabaldon-Limas and T. A. Manz, Introducing DDEC6 atomic population analysis: part 2. Computed results for a wide range of periodic and nonperiodic materials, RSC Adv., 2016, 6, 45727.
74. T. A. Manz and N. Gabaldon-Limas, Introducing DDEC6 atomic population analysis: part 1. Charge partitioning theory and methodology, RSC Adv., 2016, 6, 47771.
75. T. A. Manz and N. Gabaldon Limas, Chargemol program for performing DDEC analysis, Version 3.4.4, 2016, ddec.sourceforge.net.
76. A. A. El-Barbary, R. H. Telling, C. P. Ewels, M. I. Heggie and P. R. Briddon, Structure and Energetics of the Vacancy in Graphite, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 144107.
77. Y. Ma, P. Lehtinen, A. Foster and R. Nieminen, Magnetic Properties of Vacancies in Graphene and Single-Walled Carbon Nanotubes, New J. Phys., 2004, 6, 68.
78. M. Hjort and S. Stafström, Modeling Vacancies in Graphite via the Hückel Method, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 14089.
79. E. H. Lieb, Two Theorems on the Hubbard Model, Phys. Rev. Lett., 1989, 62, 1201.
80. F. Banhart, J. Kotakoski and A. V. Krasheninnikov, Structural Defects in Graphene, ACS Nano, 2010, 5, 26.
81. E. Kaxiras and K. C. Pandey, Energetics of Defects and Diffusion Mechanisms in Graphite, Phys. Rev. Lett., 1988, 61, 2693.
82. P. A. Thrower and R. M. Mayer, Point Defects and Self-Diffusion in Graphite, Phys. Status Solidi A, 1978, 47, 11.
83. S. Kattel, P. Atanassov and B. Kiefer, Stability, Electronic and Magnetic Properties of In-Plane Defects in Graphene: A First-Principles Study, J. Phys. Chem. C, 2012, 116, 8161.
84. L.-J. Zhou, Z. Hou and L.-M. Wu, First-Principles Study of Lithium Adsorption and Diffusion on Graphene with Point Defects, J. Phys. Chem. C, 2012, 116, 21780.
85. G.-D. Lee, C. Z. Wang, E. Yoon, N.-M. Hwang, D.-Y. Kim and K. M. Ho, Diffusion, Coalescence, and Reconstruction of Vacancy Defects in Graphene Layers, Phys. Rev. Lett., 2005, 95, 205501.
86. K. T. Chan, J. B. Neaton and M. L. Cohen, First-Principles Study of Metal Adatom Adsorption on Graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 235430.
87. C. Kittel, Introduction to Solid State Physics, John Wiley & Sons Inc., United States of America, 1996.
88. Q. Sun, Q. Wang, P. Jena and Y. Kawazoe, Clustering of Ti on a C₆₀ Surface and its Effect on Hydrogen Storage, J. Am. Chem. Soc., 2005, 127, 14582.
89. G. J. Leigh and N. Winterton, Modern Coordination Chemistry, The Legacy of Joseph Chatt, Royal Society of Chemistry, Cambridge, UK, 2002.
90. D. Michael and P. Mingos, A Historical Perspective on Dewar's Landmark Contribution to Organometallic Chemistry, J. Organomet. Chem., 2001, 635, 1.
91. M. Yoon, S. Yang, E. Wang and Z. Zhang, Charged Fullerenes as High-Capacity Hydrogen Storage Media, Nano Lett., 2007, 7, 2578.
92. H. Lee, J. Ihm, M. L. Cohen and S. G. Louie, Calcium-Decorated Carbon Nanotubes for High-Capacity Hydrogen Storage: First-Principles Calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 115412.
93. J. Klimeš, D. R. Bowler and A. Michaelides, Chemical accuracy for the van der Waals density functional, J. Phys.: Condens. Matter, 2010, 22, 02220.

---