Searching for pure iron in nature: the Chelyabinsk meteorite

Abstract

Herein we aimed to use thermomagnetic analysis (TMA) to determine the nature of iron and nickel in the Chelyabinsk meteorite, and their effect on the meteorite's magnetism. Our magnetic measurements show that 3% of the meteorite is metallic and consists of two ferromagnetic phases with Curie temperatures of T_C1 = 1049 K and T_C2 = 800 K. Using an Fe–Ni phase diagram, we show that the lower of the two temperatures is due to an Fe–Ni alloy with 51% Ni, while the higher Curie temperature phase is due to a pure or nearly pure (Ni-free) iron phase, for which we can be certain the Ni content is less than 1%. X-ray absorption (XAS) measurements show there are two clearly distinct iron oxidation environments: metallic and 2+, with the 2+ regions differing significantly from the standard FeO phase. We also demonstrate that beneath the immediate surface, iron exists virtually entirely in a metallic state. We are then able to estimate the surface composition using XPS, for which we found that 10% of iron on the surface is still surprisingly unoxidized. Finally, our theoretical calculations show how the density of states for both Fe and Ni atoms is affected for different nickel concentrations.

---

1 Introduction

Pure (impurity-free) iron in nature has never been unambiguously found, and all forms of pure iron we have today are the result of manmade processes. Alloyed iron materials in nature have been the subject of many theories, from meteorite impact to chemical reaction between magma and carbonaceous sediments (decomposed plants turned to rock by heat and pressure over time).¹ To date, very few measurements suggesting near Ni-free iron have been made. There are, however, many reports regarding the existence of metallic (alloyed) iron in meteorites, which are usually identified with measurements of magnetic susceptibility,^2–4 X-ray diffraction,⁵ photoemission,⁶ and Mössbauer spectroscopy.⁷ The existence of metallic iron is always discussed in the context of Fe–Ni alloys, with the resistance to oxidation (rusting) being due to the nickel impurities (similar to stainless steel).

The existence of pure iron (without Ni impurities) in any type of meteorite has not been well established. Experimental methods such as XPS or Mössbauer spectroscopy are extremely difficult to use to detect pure iron because the charge of iron atoms, as well as the binding energies of core level electrons are nearly identical in pure Fe and Fe–Ni alloy.⁸ The only way the distinction can be made between pure Fe-metal and Fe–Ni alloy is with temperature dependent measurements of magnetic susceptibility. That is, pure Fe and Fe–Ni alloys have different Curie temperatures—the temperature at which a material ceases to be ferromagnetic when heated. In the present paper such measurements are performed for the Chelyabinsk meteorite. Specifically, we include the more interesting higher temperatures related to the Curie temperature of pure iron not performed in previous studies.^9,10

The well known meteorite entered Earth's atmosphere on February 15th, 2013 after an intense impact event broke it off its parent body millions of years ago—an event that eventually led to a collision path with Earth.¹¹ Several buildings were damaged, and well over a thousand people were injured by the shockwave, the resulting broken glass, and the thousands of fragments strewn over the area.¹² The largest piece found was 540 kg, recovered from the bottom of Lake Chebarkul; in total, approximately 1000 kg of the meteorite were recovered.¹³ It was classified as an LL ordinary chondrite.¹⁴ This type of meteorite is distinguished from others primarily by the abundance of metal present (≈2%), and the average chondrule diameter (0.6 mm); chondrules are small round masses of olivine or pyroxene.^15,16

2 Experimental details

For our measurements we used an individual 7 g piece of the Chelyabinsk meteorite. The magnetism of the sample was measured from T = 2 to 1300 K with a slowly increasing temperature such that the entirety of the sample was at a uniform temperature. They were performed at the Institute of Metal Physics, Yekaterinburg using Quantum Design's MPMS-XL magnetic property measurement system. These measurements were performed last so the sample would not be chemically or magnetically altered for our other measurements.

X-ray photoelectron spectroscopy (XPS) core-level measurements were performed using a spectrometer based on a classic X-ray optic scheme with a hemispherical quartz monochromator and an energy analyzer working in the range of binding energies from 0 to 1400 eV. This apparatus uses electrostatic focusing and magnetic screening to achieve an energy resolution of ΔE ≤ 0.5 eV for Al Kα radiation (1486.6 eV). The samples were introduced to vacuum (10⁻⁷ Pa) for 24 hours prior to measurement, and only samples whose surfaces were free from micro-impurities were measured and reported herein. The XPS spectra were recorded using Al Kα X-ray emission photons with the spot size on the sample being 100 μm in diameter. An ion neutralizer was used to study the non-conducting samples, and typical signal to noise ratios were greater than 10 000 : 3. Finally, the spectra were processed using ULVAC-PHI MultiPak Software and CasaXPS. The nature of XPS allows for a probing depth of only roughly 3–5 nm, due to the inelastic mean free path of excited electrons, and is thus a very surface sensitive technique.

The X-ray absorption spectroscopy (XAS) measurements were taken at the Resonant Elastic and Inelastic Scattering (REIXS) beamline at the Canadian Light Source. This beamline has an undulator source and the spectrometer uses Rowland circle geometry to disperse the outgoing photons on an energy dispersive microchannel plate detector at an angle of 90° to the incoming photons. Similarly, the X-ray emission (XES) measurements were performed using Beamline 8.0.1 at the Advanced Light Source (ALS) at the Lawrence Berkeley National Laboratory with the same specifications as above.¹⁷ However, Beamline 8.0.1 offers significantly more flux that allowed us to perform the lower yield XES measurements. The main difference between beamlines is the spot size: REIXS's beam spot size is 60 × 10 μm, whereas at Beamline 8.0.1 the spot size is 100 × 1000 μm. This provides some context for the areas probed with each technique given that the metallic grain sizes on the meteorite are on the order of about 50 × 50 μm.¹⁸ Linearly polarized light was used at both beamlines and the samples were held at ultra high vacuum of ∼10⁻⁸ Torr. All XES and XAS spectra were calibrated on the energy scale by measuring standard oxides with well-known calibrations and adjusting accordingly.

3 Magnetic measurements

3.1 Thermomagnetic analysis

Thermomagnetic analysis (TMA) is a technique that involves the heating of a sample under a magnetic field and observing the temperatures where the ferromagnetism declines rapidly; this decrease is an indication that the Curie temperature was reached.^19–21

Fig. 1 shows these decreases in magnetization. The meteorite consists of three magnetic phases—signified by sudden decreases in magnetization as temperature increases. The initial drop at low temperatures is due to paramagnetic compounds in the meteorite, such as chromite, which is only ferromagnetic at very low temperatures, and is of little interest for our present purposes.²²

Fig. 1 Temperature dependence of magnetization of the Chelyabinsk meteorite measured at H = 10 kOe. Inset: dependence. The yellow block shows the error associated with the measurement, leading to a minimum Curie temperature of 1042 K for the higher of the two Curie temperatures, this temperature is very close to that of pure iron (1043 K). The error also corresponds to the yellow bar in Fig. 2.

The Curie temperatures T_C of the two significant drops at higher temperatures correspond to minima of dM/dT.²³ This derivative is shown in the inset in blue; the minima are at T_C1 = 800 K and T_C2 = 1049 K. The 800 K value corresponds to the Curie temperature of taenite—an Fe–Ni alloy with 51% Ni in this case—as shown by a blue dot in the phase diagram of Fe–Ni alloys (Fig. 2). The latter value is near the Curie temperature of metallic iron, but also close to the Curie temperature of kamacite (an Fe–Ni alloy with less than 10% Ni).

Fig. 2 Fe–Ni alloy phase diagram. The black lines separate regions of various crystal structures as a function of temperate and Ni content. The red lines show the Curie temperatures for the respective temperature and Ni content. The two blue dots correspond to the two phases of iron we find experimentally: the 49% Fe–51% Ni alloy, and the 100% ± 1% Fe. Inset: an enlarged version of the very upper left corner to display the error associated with the TMA analysis of Fig. 1. Our experiment suggests 0% Ni, but could be as high as 1% including the error.

The phase diagram of Fig. 2 was reproduced using the most reliable possible information contained in the aggregate studies of Fe–Ni alloys in ref. 24–27. Although it needs to be noted that all experimental data of Fe–Ni Curie temperatures are over 70 years old today, and the most often cited value of T_C = 1043 K (ref. 28) for pure iron may be slightly different than our modern measurements.

Indeed, as can be seen from the phase diagram (Fig. 2), the Curie temperature of kamacite converges to the Curie temperature of pure iron as the amount of Ni in the kamacite decreases (kamacite may exist at any Ni percentage below ≈35%). Our experimental value of 1049 K is higher than that of often cited pure iron at 1043 K. This may seem troublesome at first, but it can be readily explained as the result of our (and others dated) experiment, as will be discussed in detail in the following paragraph. To test for this we also performed TMA measurements on another extremely pure man-made iron sample (refined carbonyl iron; 99.93% iron). This pure iron magnetization curve is shown overlaid and scaled down by a factor of 0.0112 on the meteorite's curve. They are nearly identical matches, but the most convincing evidence is displayed in the inset. The first derivative minimum of the pure iron is <0.5 K from the minimum of the meteorite. This is less than any experimental error, so for all intents and purposes they are essentially equal.

To quantify any error in our experiment we have chosen the steepest points in the first derivative (Fig. 1 inset), i.e. the maxima of the second derivative. This is where the magnetization begins to drastically decrease, and is shown by the yellow background in the figure. From this analysis we can put the absolute lowest possible Curie temperature at 1042 K. The inset of Fig. 2 is an enlarged version of the upper left corner, shown for clarity, it also corresponds to this same error, but converted from Curie temperature to the corresponding Ni percentage. From this inset we can see that the worst possible case is that there may be up to 1% Ni. But of course, as noted by the analysis of ref. 29, we would not expect the meteorite to have kamacite/iron at a single Ni-concentration, but rather some range in the inhomogeneous sample. Although our experiment is mostly in accordance with the authors of that study, they fail to make the connection to the extremely unique finding of pure, unalloyed iron in the meteorite. Therefore, while our measurements indicate that pure iron (no Ni impurities) is present, the associated error puts a cap on the Ni content at less than 1% in the host Fe metal in some regions within the sample.

To discuss this point further: because the meteor is a product of nature, and thus not uniform in composition, we expect it to contain a spectrum of Fe–Ni phases. That is, the 51% Ni phase (taenite) likely consists of several domains hovering around 51%. This is clear from the inset of Fig. 1, which does not show an immediate and extremely sharp drop in magnetization, but instead an initial slight decline followed by a drastic decrease. This is the natural shape of a curve indicative of a Gaussian spread of inhomogeneities in the sample.²³ Remembering that TMA measures the entire bulk of the sample at once, this means that the meteorite contains regions of taenite between 48% and 54% Ni—corresponding to the temperature range in which the magnetization continues to drop. The temperature with the most significant drop in magnetization (800 K), corresponds to the greatest mass of Ni-content in the taenite regions. In other words, only observing the regions of taenite, the most common concentration of Ni-content is 51%, with regions of Ni concentration existing slightly below and above that value.

The exact same analysis can be performed observing only the more interesting low-Ni-kamacite to pure iron gradient regions of the sample. The magnetization drops between ≈1020 K and 1077 K (Fig. 1); this corresponds to a Ni-content between 0% and up to 12%, with the most common being 0% (the minimum of the first derivative). Although in this case, we add error bars using peaks in the second derivative to display the range in which the magnetization drops most drastically. This error was explained to be 1% in the preceding paragraphs. Therefore, our experiment tells us that there are indeed regions of very pure iron (≪1% Ni) surrounded by smaller regions of alloyed Ni–Fe.

In addition to the above information, we can also determine the amount of iron by plotting the pure iron curve in Fig. 1 of M(T) back to 300 K (red line). The value of M here is 2.4 emu g⁻¹. At the same time it is well known that the saturation magnetization value of iron at room temperature is 217 emu g⁻¹ (ref. 30) (we use cgs units where 1 emu g⁻¹ = 1 Am² kg⁻¹); this is in accordance with our experiment as the curve in Fig. 1 is scaled by 0.0112. From these facts we can conclude that a good estimate for the amount of high Curie temperature very pure iron in the sample is 2.4/217 = 1.1% by mass.

The second ferromagnetic phase at 800 K contributes 2.9 emu g⁻¹ at 300 K (the difference between the red dots in Fig. 1). The magnetic saturation of an Fe–Ni alloy with roughly the nickel content we see here is ≈140 emu g⁻¹.³¹ Therefore, the quantity of this second phase can be estimated at 2.9/140 = 2.1% by mass. Hence, the total amount of metal (1.1 + 2.1 = 3.2%) is within the range of the classifying this meteorite as an LL chondrite.

3.2 Curie–Weiss law

Fig. 3 examines of the Chelyabinsk meteorite with respect to the Curie–Weiss law. This describes the magnetic susceptibility of a ferromagnet in the paramagnetic regime above the Curie temperature according to the equation 1/χ = (T − Θ)/C (where C and Θ are the Curie and Weiss constants, respectively).³² The linear nature of the law holds very well in the range T > T_C1. However, the Weiss constant Θ would normally equal the Curie temperature Θ ≈ T_C in pure iron, whereas for the Chelyabinsk meteorite Θ = 49 K ≪ T_C1. This is due to the fact that the measurement probes the entire sample, which contains many other compounds. Thus, we can conclude that the measured susceptibility at high-temperatures is primarily due to other paramagnetic centers in the sample. This is supported by the sharp decline in magnetization at low temperatures in Fig. 1.

Fig. 3 The reciprocal of the magnetic susceptibility with temperatures in the paramagnetic regime (T > T_C1). The linear nature of the law (see text) holds as it should for ferromagnetic materials. Our calculation of magnetic moment per atom from the Curie constant obtained here is 2.19 μ_B. Inset: the low temperature dependence of χ × T. The slope χ₀ agrees with the overall magnetization of the sample at room temperature found in Fig. 1. The y-intercept value C leads us to the conclusions that the paramagnetic part of the meteorite is saturated with spin 1/2 magnetic centers.

We have found that the vast majority of the sample is paramagnetic with weak exchange interactions (although we cannot totally rule out a ferromagnetic component with a very small Curie temperature). In fact, we can estimate the effective magnetic moment per atom (in the paramagnetic regime) quite easily using μ_eff² = 8Cm (where m is the average atomic weight per magnetic atom in the material).³³ If we assume all the ferromagnetism is due to iron and nickel atoms, then m ≈ 57 amu and we obtain μ_eff = 2.19 μ_B.

As was mentioned earlier, and shown in Fig. 1, there is a sharp rise in magnetization when going to very low temperatures. For T < 200 K ≪ T_C the magnetization of the ferromagnetic phases remains effectively unchanged, and the sharp increase of M(T) is due to paramagnetic centers. We can then write χ = χ₀ + C/T, where χ₀ = (M_S1 + M_S2)/H + χ_add = const. (χ_add is an additional susceptibility, either diamagnetic or paramagnetic). In this case, we should expect a linear dependence of χ × T. We observe this experimentally (Fig. 3); the χ₀ value (slope) is 5.3 × 10⁻⁴ cm³ g⁻¹, which is in quite good agreement with our previous experimental value of M_S1 + M_S2 = 5.5 emu g⁻¹ (upper red dot in Fig. 1), equivalent to (M_S1 + M_S2)/H = 5.5 × 10⁻⁴ cm³ g⁻¹. Using the value of the y-intercept from this plot, C = 0.0069 Kcm³ g⁻¹, we find that for paramagnetic centers . This, combined with the fact that in the spin-only approximation S = 1/2 and S = 1 correspond to μ_eff = 1.73 and 2.83 μ_B, respectively, leads us to conclude that the paramagnetic component of the meteorite contains paramagnetic atoms, each with a magnitude of spin 1/2—that is, each atom contributes one free electron to the magnetic moment.

In summary, we have shown that the Chelyabinsk meteorite has essentially an identical Curie temperature with that of pure iron. Since the Curie temperature decreases as impurities are introduced, we can be certain that there are regions in the meteorite that contain iron phases with an extremely small amount of impurities (mainly nickel at ≪1%). This pure phase of iron has be determined to be 1.1% of the meteorite by mass. Such pure iron has never been found naturally occurring and this represents a significant discovery of a relatively rarely occurring elemental form in our universe.

4 Spectroscopic measurements

4.1 X-ray emission measurements

The chemical state of Fe-atoms can be determined with Fe L_2,3 X-ray emission measurements (XES) (3d → 2p_3/2,1/2 decay). The depth probed by XES measurements is about ten times deeper than what is probed by XPS measurements, which only probe the sample to a depth of about 20–30 Å due to the much smaller escape depth of electrons compared to that of photons. Since the beam spot size used here was quite large (100 μm × 1000 μm), we are probing all types of surface domains simultaneously.

Firstly, we look at the I(L₂)/I(L₃) intensity ratio (see Fig. 4 and Table 1 for tabulated integrated intensity ratios). It is related to the probability of radiationless L₂L₃M_4,5 Coster–Kronig (C–K) transitions, and the ratio of total photoabsorption coefficients (μ₃/μ₂) for excitation energies at the L₂ and L₃ absorption thresholds.³⁴ Since the ratio of total photoabsorption coefficients depend only on the excitation energy, the I(L₂)/I(L₃) intensity ratio of RXES spectra taken at the same excitation energy is determined by the C–K transitions alone, which are governed by the number of free d-electrons around a target atom. The I(L₂)/I(L₃) ratio of Fe atoms in a conducting (metallic) state (Fe atoms only interact with other Fe atoms) is therefore highly suppressed. On the other hand, the Fe atoms in the insulating state (Fe–O interaction) show a much larger I(L₂)/I(L₃) ratio (Fig. 4).

Fig. 4 Fe L_2,3 X-ray emission spectra of Chelyabinsk meteorite and reference compounds excited at the L₂-threshold (RXES) and far above the absorption edge (NXES). The ratio of peak heights in the meteorite sample are nearly identical with that of Fe metal. The large beam spot size and bulk sensitivity of this technique, along with the shape of the spectra, demonstrates clearly that beneath the first several atomic layers, the iron is unoxidized in a metallic state.

Table 1 Integrated I(L₂)/I(L₃) ratios for the XES spectra shown in Fig. 4. The smaller ratio in metallic iron compared to the Fe-oxides is indicative of a more conducting Fe state (see text for further discussion of this phenomenon). Our meteorite sample also displays this high degree of conductivity, and therefore is largely found in a metallic state as well

	RXES	NXES
Fe-metal	0.45	0.17
Meteorite	0.41	0.18
FeO	1.16	0.30
Fe2O3	1.39	0.27

---

Based on these measurements it can be concluded that the I(L₂)/I(L₃) ratio both in RXES and NXES spectra of Chelyabinsk meteorite are quite similar to those of metallic iron, but very different from the Fe-oxides. This indicates that metallic iron exists in significant proportions beneath the first several atomic layers, and Fe-oxides are in such low concentrations that we cannot even detect them. That is, we expect the phases of taenite and kamacite-pure iron to exist throughout the entire bulk of the meteorite, with extremely low amount of oxidized iron.

4.2 X-ray absorption measurements

Proceeding to X-ray absorption (XAS) measurements, which is a complementary technique to X-ray emission. It supplies us with similar oxidation and chemical information at the same probing depth (when measuring fluorescence yield). Although in this case our beam spot size was at least two orders of magnitude smaller by area (60 × 10 μm), so we could obtain information from individual domains in the meteorite by moving the beam location around. We found two different environments in which iron atoms were located: metallic and a 2+ oxidation state, with metallic sites being at least ten times less common than oxidized sites, as expected. However, upon probing dozens of sites, a small but detectable nickel signal was always found in the surface sensitive electron yield. It was not observable in the fluorescence yield because the nickel is extremely dilute, and fluorescence yield is roughly two orders of magnitude weaker than electron yield. Even though every metallic iron domain would be impossible to measure given time restraints, this tells us that in the given measured metallic domain there is indeed a small amount of nickel present in the metallic iron, as we would expect from the taenite regions, which are very spatially near the kamacite regions.¹⁸

Included in Fig. 5 is a crystal field multiplet calculation in agreement with the observed 2+ regions.³⁵ Interestingly, the experimental spectrum does not appear nearly identical to FeO, which we would expect, although it is clearly in a 2+ state. FeO has its iron atoms nearly perfectly octahedrally coordinated by oxygen atoms, but in order to achieve agreement with calculations, a warped octahedral environment needed to be used. Crystal field parameters used in the calculation were D_q = 0.08 eV, D_s = 0.04 eV, and D_t = −0.04 eV. These values correspond to a stretching of the surrounding octahedral crystal field along one of its axes. This stretching is significant, up to about 20% longer bond lengths along the stretched axis. Although it is still most likely bonded to oxygen atoms, this large distortion of standard FeO is likely a result of the inhomogeneous surroundings and the magnetism inherent to the sample. This new phase of FeO is something unique to this meteorite, such distorted lattices are not seen in iron oxides on Earth.

Fig. 5 Fe and Ni XAS. Two primary signals of Fe were found at different locations: metallic and 2+ sites. Upper panel: Ni was measured at the metallic sites and a small signal on the surface was found, likely due to taenite. The calculation-experimental agreement establishes that the 2+ Fe atoms are not in the standard FeO crystal environment as one might expect. Instead it is in a deformed octahedral environment, likely due to the many surrounding defects and magnetic interactions.

4.3 XPS measurements

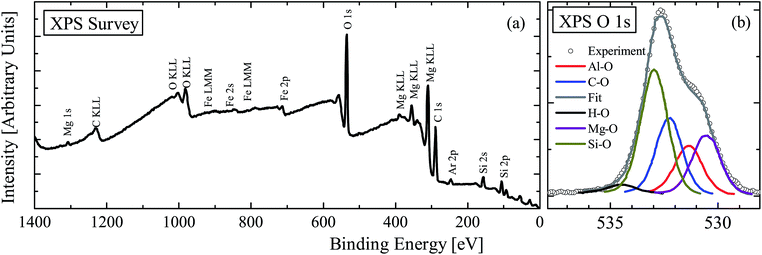
X-ray photoemission measurements probe the binding energies of the elements on the surface (first few nanometers) of a material. This technique is mainly sensitive to the oxidation state of an element. The XPS survey spectrum of the Chelyabinsk meteorite was measured for binding energies in the range of 0–1400 eV (Fig. 6(a)). Clearly present are Mg 1s, C KLL, O KLL, Fe LMM, Fe 2s, Fe 2p, O 1s, Mg KLL, C 1s, Si 2s, and Si 2p lines. Where the notation KLL corresponds to the Auger process wherein a 1s electron (K) is excited, followed by a 2s electron (L₁) decaying to fill the 1s hole, with the 2s → 1s transition energy being imparted to the emission of a 2p electron (L_2,3).

Fig. 6 (a) XPS survey spectrum showing all the major elements present (b) oxygen 1s XPS spectrum and component analysis. The areas under the curves represent the relative contributions from each of the elements bonded to oxygen.

In accordance with these data the surface composition was estimated by multiple authors using both Multipak and CasaXPS software, and the results were very similar, but were averaged, and are shown in the Table 2. The carbon signal in the XPS data is completely or nearly completely due to the sample's interaction with Earth, in which carbon is effectively everywhere, and very “sticky”, so was not included in the surface composition analysis. Also, chamber the experiment was performed in uses argon as a purging mechanism, and was also not included in the analysis.

Table 2 Surface composition of Chelyabinsk meteorite determined by XPS survey analysis. Note: carbon and argon signals were not included in the analysis as they are artifacts on the sample surface due to its interaction with Earth's environment

Element	O	Si	Mg	Al	Fe	Ni
Atomic%	65.0	17.7	10.3	4.3	2.7	0.0
Error	±1.6	±1.5	±2.1	±0.2	±0.6	±0.1

---

The beam spot size used here was 100 μm in diameter, which is relatively large in terms of the grain sizes. Therefore, this gives a reliable composition of the surface of the meteorite as a whole, in agreement with the analysis of ref. 18. It is not too dissimilar from the analysis of ref. 36, but therein a much smaller area was measured (≈7 μm × 7 μm). Notably, the XPS survey spectrum does not find the presence of nickel. Although, at sufficiently low concentrations (less than 0.1%) this technique is not sensitive enough to detect minute amounts of the metal.³⁷ So while very small amounts cannot be completely ruled out, it corroborates the magnetic findings above. Note that the carbon contamination is large, and not part of the native composition of the meteorite (anything in contact with the Earth's crust will have lots of carbon on the surface). Nevertheless, the atomic ratios of the elements in Table 2 (not including carbon) are quite reliable.

The O 1s XPS spectrum of Fig. 6 has a two peak structure due to the multiple bonding environments of oxygen. The large peak is due to C–O and Si–O bonding, whereas the low energy shoulder is the result of Mg–O and Al–O, and there is a small contribution from H–O bonding at the high energy side. The fit was performed by constraining the binding energy differences of the Mg–O, Al–O, and Si–O to their well-known values in MgO, Al₂O₃, and SiO₂. Their FWHMs were only allowed to vary a small amount from the values known for the binary oxides as well. The contributions from each of the oxygen bonding environments can be seen by the quality of the obtained fit, with the area under each curve representative of the quantity of that bonding environment.

Moving on to detailed Fe 2p XPS measurements (Fig. 7), we find contributions from Fe-metal, FeO, and Fe₂O₃, with typical charge-transfer satellites (S1 and S2).³⁸ The presence of an Fe-metal contribution confirms that some of the iron on the surface has not oxidized after being exposed to ambient atmospheric conditions for over a year. A similar effect was found forty years ago in the XPS measurements of Fe 2p spectra of lunar iron.³⁹

Fig. 7 Comparison of XPS Fe 2p spectra of Chelyabinsk meteorite (grey = experiment, pink = maximum entropy deconvolution⁴⁰) with spectra of Fe⁴¹ metal, FeO and Fe₂O₃.³⁸ The black line is a linear sum of the three components. The fit with the experimental data suggests that of the iron on the surface, 10% is metallic, 71% is in a 2+ oxidation state, and 19% in 3+.

Using linear combinations of the Fe-metal, FeO, and Fe₂O₃ an approximation of the percentage of each oxidation state on the surface can be made. This best fit linear sum is shown as the black line in Fig. 7. It is in good agreement with the maximum entropy treated spectrum (pink) of the meteorite. Thus, on the surface, looking at only the iron, a good estimate is that 10% exists in metallic form, 71% in 2+, and 19% in 3+. The 10% in metallic form is likely mostly taenite, as it is highly alloyed with nickel to resist oxidation. Therefore, the pure (or very near pure) Fe iron that contributes to the high Curie temperature phase is likely buried in the interior of the meteorite in order to resist oxidation. Much of the detected Fe³⁺ is also likely the result of Fe²⁺ oxidizing in our atmosphere. In fact, it is quite surprising that the sample is so rust resistant considering it has been exposed to so much moisture, and relatively harsh conditions since landing on Earth's surface. The exact source of this surface resistance to rusting is something that should be investigated further as rust is the source of degradation of many iron-based products we use every day.

5 Ab initio theoretical analysis

To complete the physical interpretation of our experimental data we complement our magnetic and spectroscopic results with theory. To investigate the effect of Ni on the magnetic properties of Fe_xNi_1−x alloy we computed a concentration dependence of the magnetic susceptibility within CPA + DMFT (coherent potential approximation in combination with dynamical mean-field theory).⁴² The susceptibility was calculated as a response to a small external magnetic field. We first assumed that the metallic domain of the meteorite is a solid solution of iron and nickel, and thus should be treated as an alloy. CPA + DMFT accounts for the disorder of atoms and the strong Coulomb interaction between electrons in partially filled shells of Fe and Ni. More details on the methods of dynamic and static mean field theories can be found in ref. 43 and 44.

Herein we consider two characteristic values of Fe concentration (by atomic%) in the alloy: 75% and 95% Fe. Shown in Fig. 8 is the comparison of 3d spectral functions of pure metallic Fe and Ni obtained by the standard band technique (GGA – generalized gradient approximation) and those of Fe_xNi_1−x computed within CPA + DMFT. According to GGA (Fig. 8, shaded regions) the 3d spectral functions of Ni and Fe are qualitatively similar in shape and form a common band with a total width of 4 eV for Ni, and 5 eV for Fe.

Fig. 8 (Upper panel): The total 3d and element-resolved 3d (lower and middle panels) spectral functions of Fe_xNi_1−x (x = 0.95, 0.75) as obtained in CPA + DMFT, shown by black and red lines (normalized in units of [states per eV atom]). The GGA results of elemental Fe and Ni are presented as shaded areas. Alloying iron and nickel causes small changes and shifts to the density of states, which could be measured by high resolution XPS.

For the alloys, disorder and correlations smear the fine details of the GGA spectral functions and shift some of their features. In particular, for both Fe and Ni, in both alloy concentrations, the GGA multi-peak structure in the energy window [−4, −1] eV turns into one broad feature in which intensity decreases with increasing Ni content. In the case of Ni (lower panel) the inclusion of disorder and correlation effects severely dampens the features in the [−1, +1] eV range. In contrast, the same region of the Fe spectral function is less sensitive to disorder and correlations and to a greater degree preserves the form obtained within GGA. The overall form of the total 3d spectral functions in the alloy (Fig. 8, upper panel) shows a mild concentration dependence, and the position of its features is very similar to those of Fe in the middle panel. Because of the similarity of the curves in the upper panel, we would expect only a very small shift in XPS peaks between quite large differences (5% and 25%) of nickel content. This change has been observed, but it is subtle, and high resolution along with great care in calibrating between spectra would be required.^8,45 In cases such as the Chelyabinsk meteorite, where the Ni content is minimal, the task becomes even more challenging.

6 Conclusion

Whether or not unalloyed iron exists in nature is a crucial question regarding the composition of extra-terrestrial objects. It has been scarcely considered as something to search for despite being one of the most important elements in our daily lives, especially since refining techniques have been developed to manufacture nearly pure iron from iron ores. Notwithstanding, the search for pure iron in our celestial objects could help answer basic questions regarding the formation and relative composition of such rocky objects in our solar system, as well as direct experimental evidence resulting from large objects colliding at extreme speeds in vacuum—a relatively frequent event in space that cannot be reproduced on Earth. Herein we have shown that it is extremely likely that this meteorite (and therefore probably many others) contain domains of pure, or very near pure iron within them. This should garner interest in several fields: cosmology, astronomy, physics, chemistry, and the geosciences; all of which are concerned with the elemental makeup of our universe.

Acknowledgements

The CPA-DMFT calculations, XPS and magnetic measurements were supported by Russian Science Foundation (Project 14-22-00004). The XAS measurements were performed at the Canadian Light Source, and XES measurements were performed at the Advanced Light Source, both were supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) and the Canada Research Chair program.

References

1. U. Chandra and G. Parthasarathy, AIP Conf. Proc., 2009, 1195, 886.
2. R. K. Verma and S. Prasad, J. Geophys. Res., 1975, 80, 3755.
3. D. Abbott, R. Mazumder and D. Breger, Lunar and Planet. Sc. XXXVII Conf., 2006, vol. 37, p. 1889.
4. P. Rochette, L. Sagnotti, M. Bourot-Denise, G. Consolmagno, L. Folco, J. Gattacceca, M. L. Osete and L. Pesonen, Meteorit. Planet. Sci., 2003, 38, 251–268.
5. R. R. Jaeger and M. E. Lipschutz, Geochim. Cosmochim. Acta, 1968, 32, 773.
6. M. Kotsugi, T. Wakita, T. Taniuchi, H. Maruyama, C. Mitsumata, K. Ono, M. Suzuki, N. Kawamura, N. Ishimatsu, M. Oshima, Y. Watanabe and M. Taniguchi, IBM J. Res. Dev., 2011, 55(13), 1–13.
7. U. Chandra, P. Sharma, G. Parthasarathy and B. Sreedhar, Am. Mineral., 2010, 95, 870.
8. Y. Nagai, M. Senda and T. Toshima, Jpn. J. Appl. Phys., Part 1, 1987, 26, L1131.
9. N. S. Bezaeva, D. D. Badyukov, M. A. Nazarov, P. Rochette and J. Feinberg, Geochem. Int., 2013, 51, 568–574.
10. L. Nabelek, M. Mazanec, S. Kdyr and G. Kletetschka, Meteorit. Planet. Sci., 2015, 50, 1112–1121.
11. S. Ozawa, M. Miyahara, E. Ohtani, O. N. Koroleva, Y. Ito, K. D. Litasov and N. P. Pokhilenko, Sci. Rep., 2014, 4, 5033.
12. J. Borovicka, P. Spurny, P. Wiegert, P. Kalenda, D. Clark and L. Shrbeny, Nature, 2013, 503, 235–237.
13. M. A. Nazarov, D. D. Badyukov, N. N. Kononkova and I. V. Kubrakova, Meteoritical Bulletin, 2013, 102, 1662.
14. O. P. Popova, P. Jenniskens, V. Emel'yanenko, A. Kartashova, E. Biryukov, S. Khaibrakhmanov, V. Shuvalov, Y. Rybnov, A. Dudorov and V. I. Grokhovsky, et al., Science, 2013, 342, 3132.
15. D. W. Mittlefehldt, Rev. Mineral. Geochem., 2008, 68, 571.
16. E. R. D. Scott and A. N. Krot, ASP Conf. Ser. Proc., 2005, pp. 15–53.
17. J. Jia, T. Callcott, J. Yurkas, A. Ellis, F. Himpsel, M. Samant, J. Stöhr, D. Ederer, J. Carlisle, E. Hudson, L. Terminello, D. Shuh and R. Perera, Rev. Sci. Instrum., 1995, 66, 1394.
18. V. A. Koroteev, S. V. Berzin, Y. V. Erokhin, K. S. Ivanov and V. V. Khiller, Dokl. Earth Sci., 2013, 451, 831.
19. E. Petrovsky and A. Kapicka, J. Geophys. Res., 2006, 111, B12S27.
20. R. F. Butler, Earth Planet. Sci. Lett., 1972, 17, 120–128.
21. D. E. Watson, E. E. Larson, J. M. Herndon and M. W. Rowe, Earth Planet. Sci. Lett., 1975, 27, 101–107.
22. J. Gattacceca, P. Rochette, F. Lagroix, P. Mathe and B. Zanda, Geophys. Res. Lett., 2011, 38, L10203.
23. K. Fabian, V. P. Shcherbakov and S. A. McEnroe, Geochem., Geophys., Geosyst., 2013, 14, 947–961.
24. G. Cacciamani, A. Dinsdale, M. Palumbo and A. Pasturel, Intermetallics, 2010, 18, 1148–1162.
25. L. J. Swartzendruber, V. P. Itkin and C. B. Alcock, J. Phase Equilib., 1991, 12, 288–312.
26. W. Xiong, H. Zhang, L. Vitos and M. Selleby, Acta Mater., 2011, 59, 521–530.
27. I. Garrick-Bethell and B. P. Weiss, Earth Planet. Sci. Lett., 2010, 294, 1–7.
28. CRC Handbook of Chemistry and Physics, ed. W. M. Haynes, T. J. Bruno and D. R. Lide, Taylor and Francis Group, LLC, 95th edn, 2014.
29. N. S. Bezaeva, D. D. Badyukov, M. A. Nazarov, P. Rochette and J. Feinberg, Meteorit. Planet. Sci., 2014, 49, 958–977.
30. J. Crangle and G. M. Goodman, Proc. R. Soc. London, Ser. A, 1971, 321, 477–491.
31. K. H. Gheisari, S. Javadpour and J. T. Oh, J. Phys.: Conf. Ser., 2009, 153, 012051.
32. N. N. Lubinskii, L. A. Bashkirov, A. I. Galyas, S. V. Shevchenko, G. S. Petrov and I. M. Sirota, Inorg. Chem., 2008, 44, 1015–1021.
33. V. Kusigerski, V. Spasojevic and M. Mitric, J. Phys.: Condens. Matter, 1996, 8, 10581.
34. E. Z. Kurmaev, A. L. Ankudinov, J. J. Rehr, L. D. Finkelstein, P. F. Karimov and A. Moewes, J. Electron Spectrosc. Relat. Phenom., 2005, 148, 1.
35. R. J. Green, G. S. Chang, X. Y. Zhang, A. Dinia, E. Z. Kurmaev and A. Moewes, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 115207.
36. D. A. Pavlov, A. I. Bobrov, N. V. Malekhonova, A. V. Pirogov and A. V. Nezhdanov, Sci. Rep., 2014, 4, 4280.
37. A. G. Shard, Surf. Interface Anal., 2014, 46, 175–185.
38. R. Zimmermann, P. Steiner, R. Claessen, F. Reinert, S. Hufner, P. Blaha and P. Dufek, J. Phys.: Condens. Matter, 1999, 11, 1657.
39. A. P. Vinogradov, V. I. Nefedov, V. S. Urusov and N. M. Zhavoronkov, Proceedings of the Third Lunar Science Conference, 1972, vol. 2, p. 1421.
40. J. Laverock, A. R. H. Preston, D. Newby Jr, K. E. Smith and S. B. Dugdale, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 235111.
41. A. N. Hattori, K. Hattori and H. Daimon, Surf. Interface Anal., 2008, 40, 988.
42. A. S. Belozerov, A. I. Poteryaev, S. L. Skornyakov and V. I. Anisimov, J. Phys.: Condens. Matter, 2015, 27, 465601.
43. M. A. Korotin, N. A. Skorikov, V. M. Zainullina, E. Z. Kurmaev, A. V. Lukoyanov and V. I. Anisimov, JETP Lett., 2012, 94, 806.
44. A. I. Poteryaev, S. L. Skornyakov, A. S. Belozerov and V. I. Anisimov, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 195141.
45. K. Berndt, O. Brummer and U. Marx, Phys. Status Solidi B, 1978, 86, K93–K95.

---