Selective excitation and control of the molecular orientation by a phase shaped laser pulse
Abstract
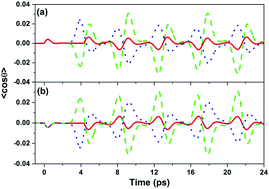
We demonstrate that the selective excitation and further control of molecular orientation can be realized by a dual-color shaped laser pulse with V-style spectral phase modulation. Due to the instructive or destructive interference between the odd and even rotational wave-packet contributions, selective excitation of the molecular orientation is realized in the half rotational periods by the V-style phase modulated femtosecond laser pulse, and the positive and negative molecular orientations can be freely switched by varying the carrier-envelope phase of the shaped laser pulse. Moreover, by varying the modulation position of the V-style phase-shaped femtosecond laser pulse, the maximum degrees of the positive and negative molecular orientation in the half rotational periods can be continuously manipulated. Our scheme can provide a new method for the manipulation of the molecular orientation induced by the phase shaped laser pulse, and also has significant applications in the control of the molecular rotational wave-packet.

 Please wait while we load your content...
Please wait while we load your content...