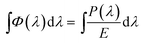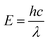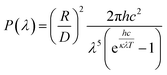DOI:
10.1039/C6RA16173A
(Paper)
RSC Adv., 2016,
6, 81976-81982
The influence of a dye–TiO2 interface on DSSC performance: a theoretical exploration with a ruthenium dye†
Received
22nd June 2016
, Accepted 17th August 2016
First published on 18th August 2016
Abstract
Density functional theory (DFT) and time-dependent DFT (TD-DFT) approaches were applied to explore the influence of a dye–TiO2 interface on DSSC performance by taking a heteroleptic Ru(II) dye as an example. Our analysis was based on the interpretation of the dye–TiO2 geometry, electronic structure, and light harvesting and utilization. The results indicate that an alkaline electrolyte is necessary if the solar cell was fabricated with an Ru dye coordinated to 2,5-bis(N-pyrazolyl)pyridine and bipyridine ligands. The higher average thermodynamic driving force of the a@(TiO2)5(OH) structure ensures a better electron injection ability. Proper modification of the acceptor ligand (4-carboxyl-pyridine fragment) not only expands the absorption coverage, but also improves the ability to capture more photons within effective absorption bands. Despite the absorption coverage being further expanded within the c@(TiO2)5(OH) geometry, the relatively weaker molar absorption coefficient reduces the light harvesting capability. The extra absorption bands in the lower energy region indicate more photons will be captured in the b@(TiO2)5(OH) structure, therefore leading to a higher short-circuit current density. Our results elucidate the effect of the dye–TiO2 interface on DSSC performance and supply a promising way to estimate and screen possible candidates for DSSC application.
1 Introduction
Due to growing demands for energy, accompanied by increasing environmental pollution and consumption of fossil fuels, the search for alternative pollution-free and renewable energy sources has become a subject of great interest. Dye-sensitized solar cells (DSSCs) have attracted attention globally because of their high photoelectric conversion efficiency, pollution-free mode of action, and bargain price since the breakthrough work reported by O'Regan and Grätzel in 1991.1 In recent years, the status of DSSCs has gradually risen to replace that of traditional solar cells. They have become a promising alternative to conventional amorphous silicon and other inorganic semiconductor-based photovoltaic devices,2–4 though their low current conversion slows down their further application. This is especially true when compared with other solid solar cells, such as the perovskite solar cell, which attains a conversion efficiency as high as 20%. From the point of view of the DSSC operating mechanism, the overall efficiency of DSSCs is controlled by the following: (a) the light harvested; (b) electron injection; (c) electron collection on the dye-semiconductor interface; and (d) dye regeneration.3,5,6 Abundant efforts have been made to overcome the bottleneck of DSSC performance by covering one or more of the above aspects. Recently, experimental investigations and theoretical design of Ru(II) center sensitizers have made great progress either by extending the π-conjugation,7 evaluating the role of ancillary ligands,8 or exploring the connection style of the dye on the semiconductor.9 Philippopoulos et al.10 synthesized and evaluated a series of heteroleptic Ru(II) sensitizers and finally concluded that the photovoltaic performance depends remarkably on the number of COOH functional groups. Our previous contribution11 indicated that it is not only the number of COOH groups, but also the substituent position on the electron donor or acceptor ligand that determines the amount of light harvested and the charge injection efficiency, thus affecting the overall efficiency of the DSSC. However, all of these conclusions are based on the electronic properties of a single dye molecule without considering other facts such as the dye-semiconductor interface, due to the computing capacity limit at that time.
Additionally, the study of different substitution sites for the auxiliary anchoring group is rarely mentioned. Considering the direct connection of the anchor group with the semiconductor, it is a crucial element of the dye–TiO2 interface to determine whether the DSSCs are high-efficiency or not. Generally speaking, the interface between the dye and semiconductor plays a vital role in reaching a higher photoelectric conversion efficiency. This is because the interface determines the position where the electron injection happens and where the charge transfer starts. There have been plenty of studies devoted to investigating the interaction between dyes and TiO2 surfaces and the charge transfer mechanism acting between them.12–28 In our current contribution, we push the previous study further by considering the dye–semiconductor interface to explore how the dye–TiO2 interface structure affects the efficiency of DSSCs.
2 Computational details
2.1 DFT and TD-DFT calculations
In this work, all the calculations were performed using the Gaussian 09 program package.29 All ground state geometries of the dye and dye@TiO2 were fully optimized with density functional theory (DFT) at the B3LYP30/LanL2DZ; 6-31G(d) level of theory, which has been successfully applied for the theoretical investigation of ruthenium dyes.11,31,32 Then at the same level of theory the harmonic vibrational frequencies were computed in order to check the nature of the stationary points, namely to check if all the frequencies were real. The electronic properties of the dye and dye@TiO2 in their excited states were explored by a time-dependent density functional theory (TD-DFT) approach. In order to select a proper functional to estimate the excitation energy, we have compared the results of the excited state based on the B3LYP, CAM-B3LYP,33 and LC-BLYP34 with LanL2DZ and 6-31G(d) hybrid basis sets. All the information for the discussion is collected in the ESI.† Solvent effects were considered by using the Polarizable Continuum Model (PCM) of SCRF procedure for dimethylsulfoxide (DMSO).
2.2 The efficiency of DSSCs
At any given wavelength λ, the incident photon to current efficiency (ηIPCE(λ)) is a function of the light harvesting efficiency (ηLHE(λ)), and the efficiency of charge injection (φinject) from the electronic excited state to the conduction band of TiO2, combined with the charge collection efficiency (ηc). (If the dye is different in the main body, but similar in the dye–TiO2 interface, the ηc can be considered to be the same.) Thus the ηIPEC(λ) can be expressed as:| | |
ηIPCE(λ) = φinjectηLHE(λ)ηc
| (1) |
Here, φinject depends on the thermodynamic driving force (D) of electrons injecting from the excited states of the dye to the semiconductor substrate.Obviously, accompanied by an increase of D, the efficiency of the charge injection would be higher, assuming the injection takes place at or near the Franck–Condon region. D can be expressed as:35| | |
D = E* − Ecb = E0 + ΔE − Ecb
| (3) |
where, E* is the redox potential in the excited state; E0 is the redox potential in the ground state, which can be calculated in accordance with the Nernst equation;11 ΔE is the vertical excitation energy which can be obtained from TD-DFT calculations; and Ecb is the conduction band edge of TiO2.
The light harvesting efficiency at the given wavelength λ can be calculated as:36,37
| | |
ηLHE(λ) = 1 − 10−Γσ(λ)
| (4) |
where,
Γ is the surface loading of sensitizers (mol cm
−2) grafted onto the semiconductor. In the current work,
Γ is set to 1.6 × 10
−7 mol cm
−2 according to a previous publication on Ru-based dyes.
10 σ(
λ) is the molecular absorption cross-section (cm
2 mol
−1). It is a function related to the molar absorption coefficient (
ε(
λ)) and can be expressed as follows:
36,38
3 Results and discussion
3.1 Geometry of the dye–TiO2 interface
As illustrated in Fig. 1, for clarity, we label the three Ru(II) complexes [Ru(bpp-1)(bpy)Cl]+, [Ru(bpp-2)(bpy)Cl]+, and [Ru(bpp-3)(bpy)Cl]+ (bpp = 2,6-bis(N-pyrazolyl)pyridine, bpp-1 = 1,1′-(4-carboxypyridine-2,6-diyl)bis(1-H-pyrazole-5-carboxylic acid), bpp-2 = 1,1′-(4-carboxypyridine-2,6-diyl)bis(1-H-pyrazole-3-carboxylic acid), bpp-3 = 1,1′-(4-carboxypyridine-2,6-diyl)bis(1-H-pyrazole-4-carboxylic acid), bpy = 2,2′-bipyridine) as a, b, and c, respectively. Accordingly, we label the corresponding dye-semiconductor structures as a@(TiO2)5, b@(TiO2)5, and c@(TiO2)5, referring to Fig. 2.
 |
| | Fig. 1 Schematic representation of dyes a, b, and c. | |
 |
| | Fig. 2 Optimized dye@(TiO2)5 structures calculated at the B3LYP/LanL2DZ; 6-31G(d) level. | |
The TiO2 surfaces are generated from the optimized bulk geometry exposing the most thermodynamically stable surface: (101) in the case of anatase. In general, nanoparticle surfaces apply the anatase (101) surface to simulate the semiconductor, because this surface has a smaller surface energy and a high efficiency for DSSCs.39,40 In the current work, anatase Ti5O2OH22 (101) models from crystal structures are adopted as the surface of the TiO2 film. In this model, the covalent bonds of the O atoms are saturated by extra H atoms, giving the Ti5O2OH22 semiconductor model. This method not only maintains bond-orientation in the crystal but also avoids the confusion of multiplicity and charge in the whole system. Additionally, these Ti atoms can be divided into two types: one is five-coordinate and the other is six-coordinate. The five-coordinate Ti atoms are located at the anatase (101) surface, which is used as the adsorption site. Meanwhile the six-coordinate Ti atoms make up the bulk of the TiO2 crystal. The calculated bond lengths dl/d2 between the two carboxylate oxygens and connected titanium atoms on the TiO2 films of the a@(TiO2)5, b@(TiO2)5, and c@(TiO2)5 systems are: 2.137/2.298 Å, 2.193/2.247 Å, and 2.192/2.255 Å, respectively. These are comparable with the Ti–O bond lengths in the dye–TiO2 interfaces calculated for larger cluster models, such as 2.12/2.10 Å for the (TiO2)256 model,41 2.08/2.08 Å for the (TiO2)36 model,42 and 2.216/2.166 Å, 2.121/2.172 Å for the (TiO2)28 model.43 This indicates that such small scale models could be sufficient to simulate the real physical properties of TiO2, and this strategy has been successfully applied in a previous study.32,44–46 Additionally, the angles of θ1 and θ2 as shown in Fig. 2 are 129.7°/131.4°, 134.2°/134.6°, and 134.3/134.5° in a@(TiO2)5, b@(TiO2)5, and c@(TiO2)5, respectively. From the point of view of bond lengths and angles, it can be concluded that the three dye–TiO2 interfaces are similar in geometry though the auxiliary anchoring groups are attached to different sites. Meanwhile, the dye–TiO2 interface is where the excited charge will be captured or collected by the semiconductor. Therefore, the similar dye–TiO2 interface geometry would lead to essentially the same charge collection efficiency (ηc) among a, b, and c.
Meanwhile in a real DSSC system, the dye–TiO2 interface may not only be affected by the electrolyte, but may also be affected by temperature and other environmental factors. As a result, the hydrogen atoms of the anchoring group of the dye molecule may be dissociated. We have calculated all possible dye–TiO2 structures which may arise from dehydrogenation processes. The calculations indicate that there are no significant changes in the bond length and angle on the dye–TiO2 interface. From this point of view, we may speculate that, whether dehydrogenated or not, this has little effect on the geometry of the dye–TiO2 interface.
3.2 Electronic structure properties
The appropriate energy level layout of the dye is one of the prerequisites for a fast charge transfer. For DSSC systems, the lowest unoccupied molecular orbital (LUMO) should be higher in energy than the lower edge of the conduction band of TiO2 (ELUMO > −4.0 eV), which should guarantee efficient electron injection from the excited dye into the semiconductor substrate. Meanwhile the highest occupied molecular orbital (HOMO) should lie between the upper edge of the valence band of TiO2, and the redox potential of I−/I3− (in the current case, −4.60 eV > EHOMO > −7.20 eV), which should guarantee efficient dye regeneration and that the excited dyes get an electron from the electrolyte rapidly. The calculated HOMO and LUMO energy values are tabulated in Table 1. The results indicate that the dye itself fully matches the above-mentioned energy level requirements, namely, there are possibilities that dyes a, b, and c could act as sensitizers in DSSCs.
Table 1 The HOMO and LUMO energy levels (in eV) for all dyes and dye–TiO2 interfaces.
| Dye |
a |
a@(TiO2)5(2H) |
a@(TiO2)5(1H) |
a@(TiO2)5(OH) |
| ELUMO |
−3.10 |
−4.06 |
−3.79 |
−3.48 |
| EHOMO |
−6.08 |
−6.33 |
−5.88 |
−5.44 |
| Dye |
b |
b@(TiO2)5(2H) |
b@(TiO2)5(1H) |
b@(TiO2)5(OH) |
| ELUMO |
−3.11 |
−4.08 |
−3.87 |
−3.69 |
| EHOMO |
−6.04 |
−6.25 |
−5.68 |
−5.21 |
| Dye |
c |
c@(TiO2)5(2H) |
c@(TiO2)5(1H) |
c@(TiO2)5(OH) |
| ELUMO |
−3.06 |
−4.04 |
−3.91 |
−3.77 |
| EHOMO |
−6.06 |
−6.26 |
−5.71 |
−5.49 |
The dye itself alone does not constitute a real DSSC. The sensitizer should be attached to TiO2 and soaked in the electrolyte at least. The energy levels of all possible dye–TiO2 structures are listed in Table 1. The calculations reveal that the HOMO and LUMO energy levels are pushed down to an even lower position by attaching the TiO2 fragment, meaning that dyes a, b, and c might not be capable of DSSC application from the point of view of their energy levels. However, if the electrolyte can be tuned into an alkaline environment, the energy value of the LUMO would be higher than −4.0 eV, as shown in the last two rows in Table 1, which means that the alkaline electrolyte solution is necessary when building DSSCs with the dyes a, b, or c, otherwise the cell may not work. Therefore, in the following sections, we only talk about the dye–TiO2 structures in the forms of a@(TiO2)5(OH), b@(TiO2)5(OH), c@(TiO2)5(OH), that is to say, all the hydrogens of the carboxyl groups are dissociated.
As is known to us, the open-circuit photovoltage (Voc) is also a crucial parameter to evaluate the efficiency of a DSSC device. Proper charge population improves the Voc. The correlation of charge population and experimental Voc indicates that when more charges are populated in acceptor groups it results in a larger Voc.47 The molecular orbital composition reveals that more than 90% of the charge would populate the bpp ligands in a, b, and c. In particular, as the substituent positions of the –COOH group change on pyrazole fragments in a, b, and c, more and more charges (from 60% in a, to 68% in b, and 79% in c, see Table 2 and Fig. 3) populate the 4-carboxyl-pyridine fragment (abbreviated as, cpy), which acts as a charge acceptor fragment and a tunnel to transfer charge from the dye to the conduction band of the semiconductor. Therefore, it can be predicted that the Voc could be further improved if the cell is fabricated with dye c.
Table 2 The composition of the HOMO and LUMO for all of the isolated dyes
| Dye |
Orbital |
Composition |
| Ru |
Cl |
bpy |
cpyraa |
cpyb |
| Refers to 1-H-pyrazole-3-carboxylic acid or something similar. Refers to 4-carboxyl-pyridine. |
| a |
LUMO |
0.08 |
0 |
0 |
0.31 |
0.60 |
| HOMO |
0.64 |
0.16 |
0.13 |
0.07 |
0 |
| b |
LUMO |
0.08 |
0 |
0 |
0.22 |
0.68 |
| HOMO |
0.66 |
0.16 |
0.12 |
0.06 |
0 |
| c |
LUMO |
0.08 |
0 |
0 |
0.12 |
0.79 |
| HOMO |
0.66 |
0.17 |
0.12 |
0.06 |
0 |
 |
| | Fig. 3 The HOMO and LUMO diagrams of dyes a, b, and c at the PCM-B3LYP/Lanl2DZ; 6-31G(d) level of theory. | |
Moreover, in order to better understand the nature of the charge transfer process, we present several important orbitals in Fig. 4. As shown in Fig. 4, in the current case, the HOMO is primarily populated on the dyes, whereas the LUMO is delocalized onto the TiO2. This kind of electronic structure is consistent with dye@TiO2 electronic character in DSSC application. In other words, the electronic properties of a dye@TiO2 system can also be described by the smaller (TiO2)5 cluster model.
 |
| | Fig. 4 The HOMO and LUMO diagrams of dye@(TiO2)5 at the PCM-B3LYP/Lanl2DZ; 6-31G(d) level of theory. | |
3.3 Light harvesting and utilization
The DSSCs that are currently used to turn sunlight into electricity can only absorb and use a small fraction of that light, which means that an abundant amount of solar energy goes unused. Harvesting more energy from sunlight requires a broad band absorption which can cover as much as possible of the solar spectral irradiance in the visible and near infrared region. In this work, the fitted Gaussian type absorption curves of the dye–TiO2 interfaces are illustrated in Fig. 5 and the corresponding character vertical excitations calculated from TD-DFT are listed in Table 4. The half-width at half height is set to 0.1 eV in gaussview, so that the character molar extinction values can be compared with the experimental values. At first glance, the molar absorption coefficients decrease but the absorption bands are widened in b and c as compared with that of a. But one cannot take it for granted that all the absorption bands in the lower energy region really contribute to the photon to electricity transfer process. According to the operation mechanism of DSSCs, to guarantee a beneficial charge transfer process, on the one hand, the value of the redox potential of the dye in the excited state, E*, should be higher in value than the conduction band of the semiconductor; on the other hand, the energetics of the excited states should be high enough to provide a thermodynamic driving force (D) to accomplish the charge injection (namely, a larger D is better). If the vertical excitations which contribute to the absorption band satisfy the above-mentioned requirements, then the exact absorption band is the so-called valid absorption band. And only the valid absorption band has the ability to contribute the final photon to the electricity conversion efficiency.
 |
| | Fig. 5 The absorption spectrum at the B3LYP/LanL2DZ; 6-31G(d) level in DMSO solvent. | |
The redox potentials of a, b, and c in the ground state are calculated to be −5.08 V, −4.85 V, and −5.36 V, which are 1.08 V, 0.85 V, and 1.37 V below the conduction band of TiO2, respectively, as shown in Table 3. Therefore, the vertical excitation energy should not be less than 1.08 eV in a, otherwise the final excited state would not have enough energy to transfer the electron to the conduction band of TiO2. As reported in Table 4, the main excitation energies are greater than 1.08 eV, therefore all absorption bands of a are valid. Similarly, the absorption bands of b and c in the current case are all effective. From this point of view, it can be deemed that the electronic structure of the dye–TiO2 interface will be changed significantly by proper modification of the acceptor segment. In addition, according to eqn (2), the average driving force of a, b, and c goes in the order of a (1.82) > b (1.49) > c (1.11), indicating that a would be optimal in the performance of the charge injection.
Table 3 Calculated redox potential (E0, in V) and Gibbs free energy (ΔGsol, in au)
| Dye@(TiO2)5 |
a@(TiO2)5(OH) |
b@(TiO2)5(OH) |
c@(TiO2)5(OH) |
| ΔGsol |
0.187 |
0.178 |
0.197 |
| E0 |
−5.083 |
−4.852 |
−5.365 |
Table 4 Selected calculated excitation energies (ΔE, eV), wavelengths (λ, nm), oscillator strengths (f), and driving forces (D, eV) for all of the dye@(TiO2)5 complexes
| Dye@(TiO2)5 |
Excitationa (|CI coeff.|) |
ΔE |
D |
λ |
f |
| H represents HOMO, L represents LUMO. |
| a@(TiO2)5(OH) |
H → L+9(0.63) |
2.35 |
1.27 |
527 |
0.1056 |
| H−1 → L+6(0.71) |
2.52 |
1.44 |
492 |
0.0691 |
| H−1 → L+16(0.45) |
3.32 |
2.24 |
374 |
0.0375 |
| H → L+18(0.77) |
3.41 |
2.33 |
364 |
0.0146 |
| b@(TiO2)5(OH) |
H−1 → L+1(0.94) |
1.59 |
0.74 |
779 |
0.0484 |
| H−3 → L+1(0.74) |
1.86 |
1.01 |
666 |
0.0209 |
| H−1 → L+6(0.88) |
2.24 |
1.39 |
553 |
0.0903 |
| H−3 → L+6(0.88) |
2.50 |
1.65 |
496 |
0.0740 |
| H → L+16(0.63) |
2.84 |
1.99 |
437 |
0.0674 |
| H−13 → L+1(0.89) |
3.06 |
2.21 |
406 |
0.0371 |
| c@(TiO2)5(OH) |
H−5 → L+1(0.95) |
1.89 |
0.53 |
656 |
0.0127 |
| H−5 → L+5(0.85) |
2.25 |
0.89 |
552 |
0.0196 |
| H−5 → L+6(0.78) |
2.33 |
0.97 |
533 |
0.1852 |
| H−3 → L+14(0.35) |
2.92 |
1.56 |
425 |
0.0365 |
| H → L+17(0.44) |
2.98 |
1.62 |
416 |
0.0256 |
However, the weak molar absorption coefficient of c may limit light harvesting and utilization. There is another factor we should take into account, the ηLHE(λ). We have shown the ηLHE(λ) profile of each dye in Fig. 6, and it is obvious that b@(TiO2)5(OH) covers a wider range and a higher ηLHE(λ) at 600–900 nm than the others. But only taking into account ηLHE(λ) does not make any sense, because the photon number varies with the change in wavelength.
 |
| | Fig. 6 The plot of the ηLHE(λ) curves for all structures. | |
The DSSC is used to convert an excited photon into an electric current. If more photons were captured, there would be more electrons to be excited, thereby resulting in more charges being injected into the conduction band of TiO2, and finally improving the short-circuit current density (Jsc) of the solar cell. Jsc is related to the integral photon flux density (Φ(λ)) over the whole absorption coverage. The Φ(λ) is defined as the number of photons per second per unit area and per unit wavelength, and it can be evaluated using the following equation at a given wavelength (λ),
| |
 | (6) |
thus, the total photon number per second per unit area within the whole spectrum coverage can be calculated using the following equation:
| |
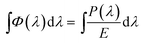 | (7) |
where,
P(
λ) is the spectral power density in W m
−2 m
−1; and
E is the energy of the photon at the wavelength of light (
λ).
E can be expressed as:
| |
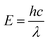 | (8) |
where,
h is Planck's constant, 6.626 × 10
−34 J s; and
c is the speed of light, 3.0 × 10
8 m s
−1.
Additionally, the maximal photon generated current (Jph) can be expressed as:
| |
 | (9) |
where,
q is the elementary charge, 1.6 × 10
−19 C.
Here, the flow of electric charge across a surface per second per unit area over the whole spectrum is equivalent to the maximum short-circuit density (Jmaxsc) the cell can produce.
On the one hand, the experimentally determined sun irradiance is too complicated to be expressed within a simple formula; on the other hand, the spectral irradiance of the sun is well approximated by the emission of a blackbody with a temperature of about 5778 K.48 Hence, the power density at the given wavelength can be rewritten as:
| |
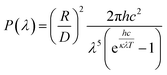 | (10) |
where,
R is the radius of the sun, 0.695 × 10
9 m;
D is the distance from the sun to the earth, 1.496 × 10
11 m;
κ is the Boltzmann's constant, 1.3806488 × 10
−23 J K
−1; and
T is the temperature of the blackbody. Here,
T = 5778 K.
In fact, the radiation absorbed by dyes is not absolutely complete, and with the consideration of the practical conditions, we introduce ηLHE(λ) for obtaining the actual absorption. From eqn (6) and (10), the exact part of the photon flux density (Φ(λ)) generated by the dyes per second per unit area at the given wavelength (λ) can be rewritten as (λ in m):
| |
 | (11) |
Finally, the Jph for a@(TiO2)(OH), b@(TiO2)(OH), and c@(TiO2)(OH) can be obtained according to eqn (9). The Jph which can be generated by a@(TiO2)(OH), b@(TiO2)(OH), and c@(TiO2)(OH) within the absorption coverage between 300–900 nm is calculated to be 15.1 mA cm−2, 31.2 mA cm−2, and 16.0 mA cm−2, respectively. As mentioned above, the flow of electric charge across a surface per second per unit area over the whole spectrum is equivalent to the short-circuit density (Jmaxsc), therefore, it can be inferred that the b@(TiO2)(OH) structure can generate the largest Jmaxsc. That is to say, the Jmaxsc of the solar cell will be further improved if the cell is fabricated with b as compared to the other two structures.
4 Conclusion
DFT and TD-DFT approaches were applied to explore the influence of the interface between the dye and the semiconductor on DSSC performance. In this work, dye–TiO2 structures with the (TiO2)5 cluster model were investigated theoretically. Though the dye–TiO2 structure remains as it was when H+ dissociates from the –COOH anchoring group due to the change of pH in the electrolyte environment, the LUMO of the dye–TiO2 structure was pushed to a higher energy level, which is advantageous for a rapid charge transfer process. More charge would populate the charge acceptor ligand (4-carboxyl-pyridine fragment) if the auxiliary anchoring group on the pyrazole fragment is located far away from the Ru(II) core. A higher average thermodynamic driving force indicates that the a@(TiO2)5(OH) structure is more conductive to electron injection. Though the absorption coverage is further expanded within the c@(TiO2)5(OH) geometry, the relatively weaker molar absorption coefficient hinders the improvement of light utilization. With the help of solar radiation's power density, our calculation reveals that a larger Jmaxsc is obtained within the absorption coverage between 300–900 nm in the b@(TiO2)5(OH) structure, namely a higher short-circuit current density could be expected if the solar cell is fabricated with dye b in an alkaline electrolyte. In a nutshell, we hope that this theoretical investigation will be helpful for improving and designing new sensitizers in DSSCs, so as to satisfy the growing demands of the DSSC field.
Acknowledgements
This work was supported by the State Key Development Program for Basic Research of China (Grant No. 2013CB834801), the Natural Science Foundation of China (Grant No. 21573088 and 21203071), and the China Post-Doctoral Science Foundation (Grant No. 2015T80297).
References
- B. O'Regan and M. Grätzel, Nature, 1991, 353, 737–740 CrossRef.
- M. Grätzel, Nature, 2001, 414, 338–344 CrossRef PubMed.
- A. Hagfeldt, G. Boschloo, L. C. Sun, L. Kloo and H. Pettersson, Chem. Rev., 2010, 110, 6595–6663 CrossRef CAS PubMed.
- G. Boschloo and A. Hagfeldt, Acc. Chem. Res., 2009, 42, 1819–1826 CrossRef CAS PubMed.
- M. Grätzel, J. Photochem. Photobiol., C, 2003, 4, 145–153 CrossRef.
- M. Law, L. E. Greene, J. C. Johnson, R. Saykally and P. Yang, Nat. Mater., 2005, 4, 455–459 CrossRef CAS PubMed.
- H. Ozawa, K. Fukushima, A. Urayama and H. Arakawa, Inorg. Chem., 2015, 54, 8887–8889 CrossRef CAS PubMed.
- T. Jella, M. Srikanth, R. Bolligarla, Y. Soujanya, S. P. Singh and L. Giribabu, Dalton Trans., 2015, 44, 14697–14706 RSC.
- J. Chen, J. Wang, F. Q. Bai, L. Hao, Q. J. Pan and H. X. Zhang, Dyes Pigm., 2013, 99, 201–208 CrossRef CAS.
- A. I. Philippopoulos, A. Terzis, C. P. Raptopoulou, V. J. Catalano and P. Falaras, Eur. J. Inorg. Chem., 2007, 5633–5644 CrossRef CAS.
- J. Wang, F.-Q. Bai, B.-H. Xia, L. Feng, H.-X. Zhang and Q.-J. Pan, Phys. Chem. Chem. Phys., 2011, 13, 2206–2213 RSC.
- C. Barolo, M. K. Nazeeruddin, S. Fantacci, D. Di Censo, P. Comte, P. Liska, G. Viscardi, P. Quagliotto, F. De Angelis, S. Ito and M. Grätzel, Inorg. Chem., 2006, 45, 4642–4653 CrossRef CAS PubMed.
- P. Qin, H. J. Zhu, T. Edvinsson, G. Boschloo, A. Hagfeldt and L. C. Sun, J. Am. Chem. Soc., 2008, 130, 8570–8571 CrossRef CAS PubMed.
- M. Nilsing, S. Lunell, P. Persson and L. Ojamae, Surf. Sci., 2005, 582, 49–60 CrossRef CAS.
- M. Nilsing, P. Persson and L. Ojamae, Chem. Phys. Lett., 2005, 415, 375–380 CrossRef CAS.
- P. Persson and M. J. Lundqvist, J. Phys. Chem. B, 2005, 109, 11918–11924 CrossRef CAS PubMed.
- M. J. Lundqvist, M. Nilsing, S. Lunell, B. Akermark and P. Persson, J. Phys. Chem. B, 2006, 110, 20513–20525 CrossRef CAS PubMed.
- P. Persson, M. J. Lundqvist, R. Ernstorfer, W. A. Goddard and F. Willig, J. Chem. Theory Comput., 2006, 2, 441–451 CrossRef CAS PubMed.
- M. Nilsing, P. Persson, S. Lunell and L. Ojamae, J. Phys. Chem. C, 2007, 111, 12116–12123 CAS.
- H. Wolpher, S. Sinha, J. X. Pan, A. Johansson, M. J. Lundqvist, P. Persson, R. Lomoth, J. Bergquist, L. C. Sun, V. Sundstrom, B. Akermark and T. Polivka, Inorg. Chem., 2007, 46, 638–651 CrossRef CAS PubMed.
- S. Ghosh, G. K. Chaitanya, K. Bhanuprakash, M. K. Nazeeruddin, M. Grätzel and P. Y. Reddy, Inorg. Chem., 2006, 45, 7600–7611 CrossRef CAS PubMed.
- M. K. Nazeeruddin, Q. Wang, L. Cevey, V. Aranyos, P. Liska, E. Figgemeier, C. Klein, N. Hirata, S. Koops, S. A. Haque, J. R. Durrant, A. Hagfeldt, A. B. P. Lever and M. Grätzel, Inorg. Chem., 2006, 45, 787–797 CrossRef CAS PubMed.
- M. S. Lowry and S. Bernhard, Chem.–Eur. J., 2006, 12, 7970–7977 CrossRef CAS PubMed.
- J. R. Li, M. Nilsing, I. Kondov, H. B. Wang, P. Persson, S. Lunell and M. Thoss, J. Phys. Chem. C, 2008, 112, 12326–12333 CAS.
- D. P. Hagberg, T. Marinado, K. M. Karlsson, K. Nonomura, P. Qin, G. Boschloo, T. Brinck, A. Hagfeldt and L. Sun, J. Org. Chem., 2007, 72, 9550–9556 CrossRef CAS PubMed.
- H. Qin, S. Wenger, M. Xu, F. Gao, X. Jing, P. Wang, S. M. Zakeeruddin and M. Grätzel, J. Am. Chem. Soc., 2008, 130, 9202–9203 CrossRef CAS PubMed.
- W. H. Howie, F. Claeyssens, H. Miura and L. M. Peter, J. Am. Chem. Soc., 2008, 130, 1367–1375 CrossRef CAS PubMed.
- H. N. Tian, X. C. Yang, R. K. Chen, R. Zhang, A. Hagfeldt and L. C. Sunt, J. Phys. Chem. C, 2008, 112, 11023–11033 CAS.
- M. Frisch, G. Trucks, H. B. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. Petersson, Gaussian 09, Revision A. 02, Gaussian, Inc., Wallingford, CT, 2009, vol. 19, pp. 227–238 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- L. Salassa, C. Garino, G. Salassa, R. Gobetto and C. Nervi, J. Am. Chem. Soc., 2008, 130, 9590–9597 CrossRef CAS PubMed.
- K. Syres, A. Thomas, F. Bondino, M. Malvestuto and M. Grätzel, Langmuir, 2010, 26, 14548–14555 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- Y. Tawada, T. Tsuneda, S. Yanagisawa, T. Yanai and K. Hirao, J. Chem. Phys., 2004, 120, 8425–8433 CrossRef CAS PubMed.
- A. Furube, R. Katoh, T. Yoshihara, K. Hara, S. Murata, H. Arakawa and M. Tachiya, J. Phys. Chem. B, 2004, 108, 12583–12592 CrossRef CAS.
- M. K. Nazeeruddin, A. Kay, I. Rodicio, R. Humphry-Baker, E. Mueller, P. Liska, N. Vlachopoulos and M. Graetzel, J. Am. Chem. Soc., 1993, 115, 6382–6390 CrossRef CAS.
- J. Zhang, J.-Z. Zhang, H.-B. Li, Y. Wu, Y. Geng and Z.-M. Su, Phys. Chem. Chem. Phys., 2014, 16, 24994–25003 RSC.
- M. Grätzel, Inorg. Chem., 2005, 44, 6841–6851 CrossRef PubMed.
- U. Diebold, N. Ruzycki, G. Herman and A. Selloni, Catal. Today, 2003, 85, 93–100 CrossRef CAS.
- M. Lazzeri, A. Vittadini and A. Selloni, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 155409 CrossRef.
- P.-P. Sun, Q.-S. Li, L.-N. Yang, Z.-Z. Sun and Z.-S. Li, Phys. Chem. Chem. Phys., 2014, 16, 21827–21837 RSC.
- N. Santhanamoorthi, K.-H. Lai, F. Taufany and J.-C. Jiang, J. Power Sources, 2013, 242, 464–471 CrossRef CAS.
- K. Chaitanya, X.-H. Ju and B. M. Heron, RSC Adv., 2015, 5, 3978–3998 RSC.
- K. Syres, A. Thomas, F. Bondino, M. Malvestuto and M. Grätzel, Langmuir, 2010, 26, 14548–14555 CrossRef CAS PubMed.
- M. Xie, J. Wang, H.-Q. Xia, F.-Q. Bai, R. Jia, J.-G. Rim and H.-X. Zhang, RSC Adv., 2015, 5, 33653–33665 RSC.
- M. Xie, J. Chen, J. Wang, C.-P. Kong, F.-Q. Bai, R. Jia and H.-X. Zhang, Theor. Chem. Acc., 2015, 134, 1–14 CrossRef CAS.
- C.-R. Zhang, L. Liu, J.-W. Zhe, N.-Z. Jin, Y. Ma, L.-H. Yuan, M.-L. Zhang, Y.-Z. Wu, Z.-J. Liu and H.-S. Chen, Int. J. Mol. Sci., 2013, 14, 5461–5481 CrossRef CAS PubMed.
- G.-S. Wu, T. Wen, Z.-W. Wang and S.-P. Liu, Telecom Power Technology, 2013, 1, 007 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra16173a |
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.