Recent application of calculations of metal complexes based on density functional theory
Abstract
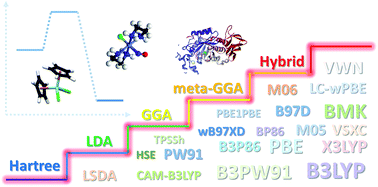
Density functional theory (DFT) has become a widely applied computational tool in most chemistry fields. Because of its applicability, DFT calculations involving metal complexes are reviewed. The achievements in the applications of DFT and the diverse DFT usage modes are shown. Developments of exchange–correlation functionals and weak interaction corrections are concisely illustrated. Moreover, practical applications of different functionals are compared and suggestions regarding the selection of functionals are presented. There are basically two methods of obtaining highly accurate exchange–correlation functionals, and borrowing the concept of orbitals from ab initio method is still unavoidable in DFT for the foreseeable future.

 Please wait while we load your content...
Please wait while we load your content...