Thermal decomposition kinetics of light polycyclic aromatic hydrocarbons as surrogate biomass tar†
Abstract
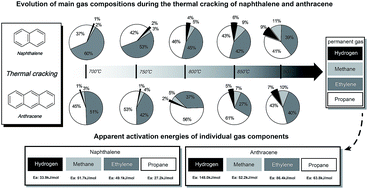
Thermal decomposition of the two light polycyclic aromatic hydrocarbons (PAHs) naphthalene and anthracene as tar model compounds was investigated with a lab-scale fluidized bed reactor. Pyrolysis kinetics for the four main gaseous products, namely hydrogen, methane, ethylene and propane, were evaluated. Experimental results indicated that naphthalene with two fused benzene rings was easier to be decomposed than anthracene with three fused benzene rings. The apparent activation energies of hydrogen, methane, ethylene and propane for naphthalene were 33.9 kJ mol−1, 51.7 kJ mol−1, 49.1 kJ mol−1 and 27.2 kJ mol−1, respectively. The apparent activation energies of hydrogen, methane, ethylene and propane for anthracene were 148.0 kJ mol−1, 52.2 kJ mol−1, 86.4 kJ mol−1 and 63.8 kJ mol−1, respectively. The most probable reaction mechanisms describing the evolution profiles of individual gas components from the pyrolysis of the two PAHs were three-dimensional diffusion for hydrogen, methane, and propane, as well as chemical reaction for ethylene.

 Please wait while we load your content...
Please wait while we load your content...