Synthesis of potential biosorbent from used stevia leaves and its application for malachite green removal from aqueous solution: kinetics, isotherm and regeneration studies
Abstract
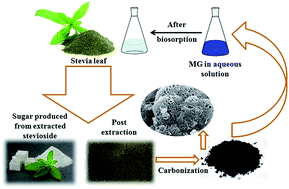
To develop a highly efficient, low-cost adsorbent from waste materials, powdered activated carbon (AC) was synthesized from used stevia leaves post the extraction of the glycosides used for producing a natural sweetener. The modification of the chemical characteristics of the biosorbent surface was achieved by impregnating it with sodium hydroxide (NaOH) at two different weight ratios. The AC biosorbent was applied for the removal of hazardous dye malachite green from an aqueous solution and the effects of the key operating parameters, such as initial dye concentration, agitation time, adsorbent dosage, solution pH, and the presence of electrolyte on the dye removal efficiency, were analyzed. The adsorption data were fitted to different isotherm and kinetic models to predict the adsorption mechanism. The Freundlich isotherm model showed the best fit to the adsorption equilibrium data and the adsorption kinetics followed a pseudo-second order model. A thermodynamic study was carried out and the data showed the endothermic and non-spontaneous nature of the process in the studied temperature range. The high adsorption efficiency shown after the regeneration studies indicated the high potential for the adsorbent to be used as a highly efficient, low-cost biosorbent.

 Please wait while we load your content...
Please wait while we load your content...