In situ monitoring of colloid packing at an air/water interface using visible laser diffraction
Chi-Chih Ho *ab,
Wen-Yi Linc and
Fan-Gang Tsenga
*ab,
Wen-Yi Linc and
Fan-Gang Tsenga
aDepartment of Engineering and System Science, National Tsing Hua University, Hsinchu, Taiwan
bNano Science and Technology Program, Taiwan International Graduate Program, Academia Sinica, National Tsing Hua University, Taiwan. E-mail: chichih@gate.sinica.edu.tw
cDepartment of Materials Science and Engineering, National Tsing Hua University, Hsinchu, Taiwan
First published on 10th August 2016
Abstract
A diffractive method using a visible laser to directly monitor colloids trapped at an air/water interface under isothermal compression is discussed. Upon merely measuring the ratio of first- and second-order diffractions on the screen, the center-to-center distance of adjacent colloids can be determined. Complicated instruments such as advanced optical microscopy, geometries of the apparatus and particle tracking analysis are not necessarily required. The equation of estimation is established based on the theory of Ewald sphere construction. Fabricating and precise monitoring of a colloidal monolayer can be achieved in parallel by this noninvasive method.
Introduction
The like-charged colloids trapped at a polar/nonpolar interface have practical applications in fabricating array-typed nanomaterials and nanostructures.1,2 The obtained nanostructure arrays can give service as functional layers in photovoltaics,3 plasmonic sensors4,5 and magnetic storage.6 Previous studies suggested that interactions among the tri-phases can cause asymmetric electrostatic stresses that deform the liquid interface,7 leading to abundant phenomena, including long-range ordering.8–10 To experimentally explore the behavior of colloids trapped at an air/water interface, advanced optical microscopy (OM) is often employed to directly visualize the trajectory of colloids,11 followed by image processing12,13 to acquire the physics. However, the resolution and scope of views are restricted to the diffraction limit at visible frequencies and the size of the lens. In addition, the analysis relies heavily on high quality images and, therefore, requires the stability of the system to be strictly controlled. The Wilhelmy plate is an alternative that can mechanically monitor the colloid packing, by the surface pressure changes that can frequently be seen in the Langmuir–Blodgett (L–B) transfer technique.14 However, the method is an invasive detection method at the local colloidal monolayer and cannot distinguish the ordering of the structure. Considering recent interest in developing the rapid fabrication of a wafer-scaled colloidal crystal monolayer,15,16 a complementary tool for efficiently inspecting and investigating the growth of a crystal or packing behavior is demanded.Previous reports have utilized visible light diffraction to noninvasively inspect the crystal quality, polycrystallinity, orientations and lattice displacement of a colloidal monolayer that was packed on a solid support.17–19 In this report, visible laser diffraction is applied to directly monitor the center-to-center distance (d) of adjacent colloids packed on a liquid surface. We discuss the interplay between d and diffraction patterns by conducting Ewald sphere construction, showing that the d value is merely associated with the incident wavelength and the distance ratio of first- and second-order diffraction spots. The method does not require the measurement of the Bragg angles, the sample-to-screen distance, or other geometries of the apparatus.20 The area of the analyzed colloidal monolayer, depending on the size of the beam spot, is often arranged in a millimeter square. Furthermore, the macroscopic lattice information of the colloidal crystal monolayer can be acquired in the presence of dynamic flow, such as a continuous dilation, compression or convection.
Experimental
For the experiment, a home-made L–B trough (32 mm by 80 mm, Teflon border) with the bottom sealed with optically transparent glass is illustrated in Fig. 1(A). The monodispersed polystyrene microsphere suspension was purchased from Thermo scientific 4010A with a diameter equal to 1019 nm and a coefficient of variation <3%. The L–B trough was then filled with Millipore deionized water (18.2 MΩ), which was first ultrasonicated for several minutes to avoid trapped bubbles. The water surface was descummed very carefully with a sucking tip to remove interfacial contamination such as dust or other amphiphilic molecules. The 4010A was concentrated to 10 wt%, followed by addition of an equal volume of ethanol. After ultrasonicating the mixture for 15 minutes, the suspension was slowly injected onto the L–B trough via a conduit plate using a syringe pump with an injection rate of around 0.5 μL per minute. By slowly moving the Teflon barrier of the L–B trough, a polycrystalline colloidal monolayer at the air/water interface with uniform and continuous coverage can thus be prepared.17,21 | ||
| Fig. 1 (A) Apparatus arrangement including L–B trough, laser beam and camera. (B) Illustration of the wave scattered by regularly-spaced PS colloids. (C) Arrangement of PS colloids on water surface. | ||
A diode laser with wavelength in the visible frequency, power around 100 mW, and spot size ∼2 mm in diameter was incident normal to the colloidal monolayer on the water surface from the bottom side. The size of a single domain can be fabricated to be larger than the laser beam size. A thin grid paper served as a projection screen that was mounted around 4 mm above the water surface to catch the diffraction spots, which were then reordered by a monochrome camera. In the present case, the monolayer is composed of regularly spaced colloids each acting as a scattering center for a grating diffraction, as depicted in Fig. 1(B) and (C).22 A high speed Phantom V7.3M camera was employed to capture the images of the colloids. The image analysis was conducted by ImageJ software and a program developed by J. Crocker et al.
Results and discussion
The compression begins with the trough being fully filled with deionized water (18.2 MΩ cm), followed by injection of an appropriate amount of PS colloid onto the water surface. Fig. 2 illustrates that the PS colloidal monolayer at the trough center undergoes a transition from a disordered state, with a non-closely packed arrangement to a close-packed hexagonal structure, while the monolayer is gradually compressed. In stage 1, the PS colloids with a low areal fraction were randomly distributed on the water surface, as evidenced by the laser beam diffraction pattern and observation of the OM image captured by the high speed camera in Fig. 2(A1 and B1). Some portions of the colloids can be ordered even without sufficient area confinement: see the iridescence around the border in stage 1, which was disclosed by previous reports.7,8 As the compression arrives at stage 2, the interparticle distance is close to the diameter of the PS colloid by the reduction of surface area. A semicrystalline feature was revealed by looking at the concentric Debye ring and OM images in Fig. 2(A2) and (B2). After reaching a sufficient compression, the monolayer film exhibited a uniform iridescent color and six-fold symmetric diffraction pattern under white light and laser beam illumination, as shown in Fig. 2(A3), indicating the existence of structural ordering. The OM images, in Fig. 2(B3), help to verify the transformation of the PS colloidal monolayer to hexagonal ordering with a non-closely packed structure. Further compression can cause the PS colloids to reduce their center-to-center distance, without destroying the local ordering, leading to a closely-packed structure, see Fig. 2(B4) in stage 4. During the interval between stages 3 and 4, the second-order diffractive spots were seen to escape from the central spot and eventually disappeared. This continuous response of diffraction patterns is the consequence of the varying periodicity in the grating made from a regularly-spaced colloidal monolayer.In this section, we apply the Ewald sphere construction to elaborate the relationship between diffraction pattern and d. The 2D colloidal crystal with a triangular lattice is defined by the primitive translation vectors (a, b). These vectors have identical length equal to d and are separated by an angle of 60° in Fig. 3(A). The corresponding reciprocal basis vectors have a unit cell defined by (a*, b*), which is given by a·b* = b·a* = 2π, as drawn in Fig. 3(B). The length of a* is reciprocal to d as follows:
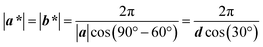 | (1) |
 | ||
| Fig. 3 (A) Triangular lattice of PS array. (B) Corresponding vectors in reciprocal space (C) and (D) 3-D sketch of Ewald sphere construction and reciprocal vectors. | ||
Owing to the lack of periodicity in the z direction in real space, a wave traveling along this direction is not continuously scattered. Therefore, the vectors along the z direction can be assumed to have any value in reciprocal space, and are pictured as hexagonally arranged columns (Bragg's rods).23,24 The diffraction condition is allowed at the intersection of Bragg's rods and the circumference of the Ewald sphere,25 as graphically sketched in Fig. 3(C). Looking closely at the Ewald construction in Fig. 3(D), two triangles ΔOO′E and ΔOO′F are observed sharing an identical sample-to-screen distance, where O, E and F are the positions of the 2D crystal sample, the first-order diffraction spot and second-order diffraction spot, respectively. Thus, the ratio of Bragg angles, the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2 and tan
θ2 and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1, can be simply calculated as r2/r1. On the other hand, the ratio of tan
θ1, can be simply calculated as r2/r1. On the other hand, the ratio of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ2 and tan
θ2 and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ1 can also be obtained from another two triangles within the Ewald sphere in reciprocal space, the triangles ΔOAD and ΔOBC. The lengths of
θ1 can also be obtained from another two triangles within the Ewald sphere in reciprocal space, the triangles ΔOAD and ΔOBC. The lengths of  and
and 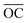 are equal to |ki| = 2π/λ, the radius of the Ewald sphere.
are equal to |ki| = 2π/λ, the radius of the Ewald sphere.
The lengths of  and
and  are the maginitudes of a* and 2a* + b*, equivalent to |a*| and
are the maginitudes of a* and 2a* + b*, equivalent to |a*| and  . Using Pythagoras' theorem to compute
. Using Pythagoras' theorem to compute  and
and  , one obtains eqn (2) below:
, one obtains eqn (2) below:
 | (2) |
By inserting eqn (1) into eqn (2), the derived center-to-center distance d is associated with r2/r1 and the length of the wave vector, as shown in eqn (3). Eventually, the geometric factors, such as the Bragg angles and screen-to-sample distance, can be eliminated from the calculations.
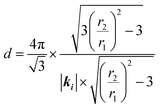 | (3) |
The validity of eqn (3) is firstly examined with PS colloids with an average diameter of 1019 nm (Thermo scientific 4010A) closely-packed on an optically transparent glass, as shown in Fig. 4(A). The colorful iridescence results from light diffracted through a 2D grating under white light illumination, also known as structural color.26 While a 470 nm-long laser was incident into the selected monocrystalline domain, a clear diffraction pattern was projected onto the screen, as shown in Fig. 4(B). By plotting greyscale intensity as a function of pixel numbers through the white broken lines in the inset of Fig. 4(B), the distances of the 1st and 2nd diffraction spots from the incident center can be estimated in Fig. 4(C). The measured r2/r1 is ∼3.65 from calculation of the peak-to-peak value of pixel numbers, producing a d value equal to 1027 nm that adequately matches the diameter of 1019 nm.
We also verified the relation between image analysis and diffraction calculation for that colloidal monolayer at the air/water interface. Fig. 5(A) is the diffraction recorded from a 532 nm-long laser passing through a non-closely packed crystal in the L–B trough. Afterwards, a microscope equipped with a high speed camera was mounted to record the arrangement of colloids at an almost identical position, as shown in Fig. 5(B). The vacancy mixture with a monolayer colloidal crystal is thermodynamically favorable. Two hundred of the acquired images were analyzed by a pair correlation function, which is depicted in Fig. 5(C), showing a nearly perfect crystal feature. The locations of the first and second peaks, from a fitted Gaussian, are 1312 nm and 2278 nm and they were theoretically assigned to d and 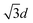 . On the other hand, according to the diffraction result, the calculated d is valued at 1265 nm by inserting the r2/r1 ratio and wavelength into eqn (3). By comparing the two experimental quantities, we calculated the percentage error to be around 3.6%, which we suggest is an acceptable error for our accuracy check.
. On the other hand, according to the diffraction result, the calculated d is valued at 1265 nm by inserting the r2/r1 ratio and wavelength into eqn (3). By comparing the two experimental quantities, we calculated the percentage error to be around 3.6%, which we suggest is an acceptable error for our accuracy check.
To demonstrate the opportunity for dynamic monitoring, a colloidal monolayer was formed on a water surface and subject to isothermal compression at a rate of 3 μm per second.27 A laser beam was incident normal to a monocrystalline domain located at the center of a Langmuir trough. Before beginning compression, the diffraction pattern can exhibit third-order diffraction spots, as shown in the top panel of Fig. 6(A). The appearance of third-order diffraction spots resulted from the third reciprocal basis vector being enclosed within the Ewald sphere, indicating a relatively large d existing in the current stage in Fig. 6(A). To clearly trace the trajectory of diffraction changes during compression, we painted the first-, second- and third-order diffraction spots as red, green and blue, respectively, using pseudo color. The superposition of diffraction patterns shows that the diffraction spots escape radially from the central spot, as shown by the direction of the arrow in the middle panel of Fig. 6(A). The phenomenon results from the reciprocal interplay between d in real space and |a*| in reciprocal space, as mentioned in eqn (1), so that reducing d can expand the size of the reciprocal lattice. The third and second spots were observed to be distinct on the screen and eventually leave the first-order diffraction spots on the screen. This is because the expanding second and third reciprocal basis vectors have traveled across the exterior surface of the Ewald sphere so that the diffraction conditions are no longer permitted. The continuous changes in r2/r1 were converted to d nm by eqn (3) until the second order diffraction spots became distinct and are plotted as a function of compression time in Fig. 6(B). The second-order diffraction spots were supposed to be extinct when the second reciprocal basis meets the surface of the Ewald sphere as the colloidal monolayer undergoes a sufficient compression. The condition can be mathematically expressed as  . Thus a critical value of d can be derived, equal to 1064 nm, which is the detection limit of a 532 nm-long laser by the present method. In the range of 1392 nm to 1064 nm, the d monotonically reduced in a non-linear fashion without breaking the local ordering and changing the crystal orientation. The trend initially reduced slowly, next shifted to a steeper slope, and then reached a constant value, where the van der Waals' attraction may predominate over the system, leading to an irreversible aggregation. The further compression can collapse the colloidal monolayer, leading to breakage, lattice distortion or multilayers, as revealed by the distorted diffraction patterns.27 Here, we demonstrated the diffractive analysis of packing behavior fixed on a local crystal. Future work would focus on the design of a mobile laser beam to perform a full surface scan during compression.
. Thus a critical value of d can be derived, equal to 1064 nm, which is the detection limit of a 532 nm-long laser by the present method. In the range of 1392 nm to 1064 nm, the d monotonically reduced in a non-linear fashion without breaking the local ordering and changing the crystal orientation. The trend initially reduced slowly, next shifted to a steeper slope, and then reached a constant value, where the van der Waals' attraction may predominate over the system, leading to an irreversible aggregation. The further compression can collapse the colloidal monolayer, leading to breakage, lattice distortion or multilayers, as revealed by the distorted diffraction patterns.27 Here, we demonstrated the diffractive analysis of packing behavior fixed on a local crystal. Future work would focus on the design of a mobile laser beam to perform a full surface scan during compression.
Conclusions
Optimizing the occasion of transferal of a colloidal monolayer onto a support is of great interest in the L–B transfer technique, which continues to play an important role in recent progress in fabricating array-typed nanomaterials.15 In addition to the existing Wilhelmy plate and advanced OM techniques, we suggest an alternative to monitor the packing behavior of colloidal material on a liquid surface using laser beam diffraction. The diffractive method has the advantages of noninvasive detection, nanoscale sensitivity and readily obtained interparticle distance from the optical response. According to eqn (3), the center-to-center distance of adjacent colloids can be read merely by relying on recording the ratio of first- and second-order diffractions, excluding the geometry of the apparatus. The accuracy of the d values was verified with close-packed and non-closely packed samples, which gave adequate agreement. The detection of d, as well as the colloid size, was limited in this method by the appearance of second-order diffraction and the nature of visible frequencies being arranged between around 400 nm and 700 nm. For example, the detecting limit of d using a purple laser with a wavelength around 405 nm is about 810 nm. Assisted by the presented diffractive method, the stage of a perfect and packed monolayer film could be judged and be deposited prior to collapse, thus lowering the transferral failure. We anticipate that the diffractive method can offer further service in mapping the crystalline state over the whole two-dimensional colloidal film to reveal the distribution of crystal orientations, bending of the lattice, accumulation of stress/strain or jammed states.Acknowledgements
We thank the instrument support from NanoCore facility, Dr Wen-Tau Juan in institute of physics and Dr Yu-Tai Tao in institute of chemistry at Academia Sinica, Taiwan.References
- J. Zhang, Y. Li, X. Zhang and B. Yang, Adv. Mater., 2010, 22, 4249 CrossRef CAS PubMed.
- A. Nemiroski, M. Gonidec, J. M. Fox, P. Jean-Remy, E. Turnage and G. M. Whitesides, ACS Nano, 2014, 8, 11061 CrossRef CAS PubMed.
- S. Jeong, E. C. Garnett, S. Wang, Z. Yu, S. Fan, M. L. Brongersma, M. D. McGehee and Y. Cui, Nano Lett., 2012, 12, 2971 CrossRef CAS PubMed.
- H.-Y. Hsieh, J.-L. Xiao, C.-H. Lee, T.-W. Huang, C.-S. Yang, P.-C. Wang and F.-G. Tseng, J. Phys. Chem. C, 2011, 115, 16258 CAS.
- C.-C. Ho, K. Zhao and T.-Y. Lee, Nanoscale, 2014, 6, 8606 RSC.
- W. G. Wang, A. Pearse, M. Li, S. Hageman, A. X. Chen, F. Q. Zhu and C. L. Chien, Sci. Rep., 2013, 3, 1948 CAS.
- M. G. Nikolaides, A. R. Bausch, M. F. Hsu, A. D. Dinsmore, M. P. Brenner, C. Gay and D. A. Weitz, Nature, 2002, 420, 299 CrossRef CAS PubMed.
- W. Chen, S. Tan, T.-K. Ng, W. T. Ford and P. Tong, Phys. Rev. Lett., 2005, 95, 218301 CrossRef PubMed.
- P. A. Kralchevsky and N. D. Denkov, Curr. Opin. Colloid Interface Sci., 2001, 6, 383 CrossRef CAS.
- R. Aveyard, B. P. Binks, J. H. Clint, P. D. I. Fletcher, T. S. Horozov, B. Neumann, V. N. Paunov, J. Annesley, S. W. Botchway, D. Nees, A. W. Parker, A. D. Ward and A. N. Burgess, Phys. Rev. Lett., 2002, 88, 246102 CrossRef CAS PubMed.
- V. Prasad, D. Semwogerere and R. W. Eric, J. Phys.: Condens. Matter, 2007, 19, 113102 CrossRef.
- W. K. Kegel and A. van Blaaderen, Science, 2000, 287, 290 CrossRef CAS PubMed.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298 CrossRef CAS.
- P. V. Petkov, K. D. Danov and P. A. Kralchevsky, Langmuir, 2014, 30, 2768 CrossRef CAS PubMed.
- P. Gao, J. He, S. Zhou, X. Yang, S. Li, J. Sheng, D. Wang, T. Yu, J. Ye and Y. Cui, Nano Lett., 2015, 15(7), 4591–4598 CrossRef CAS PubMed.
- A. S. Hall, S. A. Friesen and T. E. Mallouk, Nano Lett., 2013, 13, 2623 CrossRef CAS PubMed.
- X. Meng and D. Qiu, Langmuir, 2014, 30, 3019 CrossRef CAS PubMed.
- H. J. Schöpe, A. B. Fontecha, H. König, J. M. Hueso and R. Biehl, Langmuir, 2006, 22, 1828 CrossRef PubMed.
- F. Xue, Z. Meng, F. Qi, M. Xue, F. Wang, W. Chen and Z. Yan, Analyst, 2014, 139, 6192 RSC.
- J.-T. Zhang, X. Chao, X. Liu and S. A. Asher, Chem. Commun., 2013, 49, 6337 RSC.
- C.-C. Ho, P.-Y. Chen, K.-H. Lin, W.-T. Juan and W.-L. Lee, ACS Appl. Mater. Interfaces, 2011, 3, 204 CAS.
- B. van Duffel, R. H. A. Ras, F. C. de Schryver and R. A. Schoonheydt, J. Mater. Chem., 2001, 11, 3333 RSC.
- R. D. Meade, K. D. Brommer, A. M. Rappe and J. D. Joannopoulos, Appl. Phys. Lett., 1992, 61, 495 CrossRef CAS.
- C. Dux and H. Versmold, Phys. Rev. Lett., 1997, 78, 1811 CrossRef CAS.
- B. D. Cullity and S. R. Stock, Elements of X-ray diffraction, Prentice Hall, 2001, p. 98 Search PubMed.
- P. Vukusic and J. R. Sambles, Nature, 2003, 424, 852 CrossRef CAS PubMed.
- R. Aveyard, J. H. Clint, D. Nees and V. N. Paunov, Langmuir, 1999, 16, 1969 CrossRef.
| This journal is © The Royal Society of Chemistry 2016 |




