Binuclear iron carbonyl complexes of thialene

Abstract

Thialene (C₈H₆S) is an isomer of benzothiophene and related to azulene by replacement of a C=C unit in the seven-membered ring by a sulfur atom. The geometries of binuclear iron carbonyl complexes of thialene (C₈H₆S)Fe₂(CO)_n (n = 6, 5, 4) have been investigated using density functional theory for comparison with the corresponding azulene derivatives. The lowest energy (thialene)Fe₂(CO)₆ structures have a bis(tetrahapto)-η⁴,η⁴-thialene ligand bonded to two separate Fe(CO)₃ units without involvement of the sulfur atom. This differs from the isomeric (benzothiophene)Fe₂(CO)₆ structure known experimentally in which an iron atom has inserted into a carbon–sulfur bond to give a ferrathianaphthalene system. The only low-energy (thialene)Fe₂(CO)₅ structure has a pentahapto-trihapto-η⁵,η³ thialene ligand bonded to an Fe₂(CO)₅ unit, again without involvement of the sulfur atom. This structure is related to the experimental structure of azulene diiron pentacarbonyl, (η⁵,η³-C₁₀H₈)Fe₂(CO)₅ by replacement of the uncomplexed C=C double bond in the seven-membered ring with the sulfur atom in the thialene six-membered ring. The potential energy surface of the unsaturated (thialene)Fe₂(CO)₄ is very complicated but does not include any low-energy structures with formal Fe=Fe double bonds. Thermochemical considerations suggest (thialene)Fe₂(CO)₅ as a realistic synthetic objective, which is potentially accessible from reactions of thialene with Fe₂(CO)₉ or (benzalacetone)Fe(CO)₃ under mild conditions.

---

1. Introduction

Interaction of transition metal complexes with sulfur heterocycles is relevant, among other things, to understanding processes for the removal of sulfur from petroleum.¹ In this connection, sulfur heterocycles derived from aromatic hydrocarbons by replacement of a –CH=CH– unit with a sulfur atom, such as thiophene and benzothiophene, are among the sulfur compounds found in petroleum. For this reason the reactions of such sulfur heterocycles with various transition metal complexes are of interest.

Possible reagents for the desulfurization of aromatic sulfur heterocycles include iron carbonyls. In this connection, reactions of iron carbonyls with thiophene result in insertion of the iron atom into the C₄S ring to give initially a six-membered FeSC₄ ferrathiabenzene ring (Fig. 1). However, the initial ferrathiabenzene complex obtained from thiophene eliminates FeS to give sulfur-free tricarbonylferrole iron tricarbonyl thereby resulting in desulfurization of thiophene.² The corresponding ferrathianaphthalene complex derived from benzothiophene is stable towards an analogous desulfurization reaction.^3,4

Fig. 1 Insertion of iron carbonyl into the C₄S rings of thiophene and benzothiophene to give initially ferrathiabenzene and ferrathianaphthalene derivatives, respectively.

An isomer of benzothiophene is thialene, which is derived from azulene by replacement of a –CH=CH– unit in the seven-membered ring with a sulfur atom, thereby leading to a six-membered C₅S ring (Fig. 2).⁵ The resemblance between thialene and azulene is so close that both have an unusual deep blue color. Azulene, as a non-benzenoid aromatic hydrocarbon, is reactive towards metal carbonyls. The binuclear iron and molybdenum carbonyl complexes of azulene have been known⁶ since 1958 and have been shown by X-ray crystallography to have the (η⁵,η⁵-azulene)Mo₂(CO)₆ (ref. 7) and (η⁵,η³-azulene)Fe₂(CO)₅ (ref. 8) structures (Fig. 3). Furthermore, the complete series of binuclear (azulene)Fe₂(CO)_n (n = 6, 5, 4, 3, 2, 1) derivatives has been studied by density functional theory.⁹

Fig. 2 Relationship of thialene to azulene as compared with the relationship of thiophene to benzene.

Fig. 3 Structures of the binuclear azulene metal carbonyl complexes of iron and molybdenum.

We now report a density functional theory study of the binuclear (thialene)Fe₂(CO)_n (n = 6, 5, 4) complexes, which are the species most likely to be realized experimentally as compared with thialene complexes of other metal carbonyls. We find the six-membered C₅S ring in thialene to be much more resistant towards insertion of an iron atom as compared with the five-membered C₄S ring of the isomeric benzothiophene. In addition, the relationship between aromatic hydrocarbons and their analogous sulfur heterocycles extends to the iron carbonyl complexes for azulene and its sulfur analogue, thialene. We thus predict the product obtained from thialene and iron carbonyls to be (η⁵,η³-thialene)Fe₂(CO)₅ related to the experimentally known (η⁵,η³-azulene)Fe₂(CO)₅ by replacement of the uncomplexed –CH=CH– unit in the latter complex with a sulfur atom thereby contracting the seven-membered C₇ ring into a six-membered C₅S ring.

2. Theoretical methods

Electron correlation effects were considered by employing density functional theory (DFT) methods, which have evolved as a practical and effective computational tool, especially for organometallic compounds.^10–16 Thus three DFT methods were used in this study. The B3LYP method is the standard hybrid HF/DFT method using the combination of the three parameter Becke functional (B3) with the Lee–Yang–Parr (LYP) generalized gradient correlation functional.^17,18 The BP86 method combines Becke's 1988 exchange functional with Perdew's 1986 gradient corrected correlation functional.^19,20 The M06-L method, developed by Truhlar's group,²¹ is a hybrid meta-GGA DFT method constructed using three strategies: constraint satisfaction, modeling the exchange-correlation hole, and empirical fits. Since the M06-L energy differences among different spin states are found to be closer to experimental results,²² and various spin state structures are involved in this paper, we therefore adopt the energy order predicted by the M06-L method. However, the BP86 and B3LYP results are reported in the ESI.†

All structural optimizations were performed using double-ζ plus polarization (DZP) basis sets. The DZP basis sets used for hydrogen, carbon, oxygen, and sulfur atoms add one set of polarization functions with orbital exponents α_p(H) = 0.75, α_d(C) = 0.75, α_d(O) = 0.85, α_d(S) = 0.70 to the standard Huzinaga–Dunning contracted DZ sets.^23–25 The loosely contracted DZP basis set for iron is the Wachters primitive set²⁶ augmented by two sets of p functions and a set of d functions, contracted following Hood, Pitzer, and Schaefer,²⁷ designated as (14s11p6d/10s8p3d). The relative energies were refined with single point calculations using the M06-L functional and basis sets of triple-ζ quality, i.e. Dunning's cc-pVTZ basis sets.^28,29

Vibrational frequencies and infrared intensities were determined analytically. Since the BP86 method has been shown to predict vibrational frequencies closer to experimental values without using any scaling factors, only the BP86 ν(CO) frequencies are discussed in the text. The results obtained by the other methods are reported in the ESI.†

All computations were carried out using the Gaussian 09 program³⁰ with the ultrafine grid option for evaluating integrals numerically. Unless otherwise indicated, the optimized structures are genuine minima with no imaginary vibrational frequencies.

Each (C₈H₆S)Fe₂(CO)_n structure in the present paper is designated as nS-m or nT-m, where n is the number of CO groups, m orders the structures according to their M06-L/DZP relative energies, and S and T represents singlet and triplet spin states, respectively. Thus the lowest energy singlet (C₈H₆S)Fe₂(CO)₆ structure is designated 6S-1 and the lowest energy triplet (C₈H₆S)Fe₂(CO)₄ structure is designated 4T-1.

3. Results

3.1. (C₈H₆S)Fe₂(CO)_n (n = 6, 5)

Three low-energy (C₈H₆S)Fe₂(CO)₆ singlet structures are found, namely the trans structure 6S-1 with the two Fe(CO)₃ groups on opposite sides of the thialene ligand, and the cis structures 6S-2 and 6S-3 with the two Fe(CO)₃ groups on the same side of the thialene ligand (Fig. 4). Structure 6S-1 has the lowest energy, with structures 6S-2 and 6S-3 lying 9.7 and 17.6 kcal mol⁻¹ (M06-L/cc-pVTZ, the same below) respectively, above 6S-1. Other possible (C₈H₆S)Fe₂(CO)₆ structures were also examined. However, their energies were found to be so high (more than 20 kcal mol⁻¹ above 6S-1 by M06-L) that these structures are not likely to be chemically significant. Therefore they are not discussed in this paper.

Fig. 4 The low-energy (C₈H₆S)Fe₂(CO)₆ structures predicted by the M06-L/DZP method. The relative energies (kcal mol⁻¹) are shown in parentheses, in which the first one is from the M06-L/DZP method, and the second one is the single point energy from M06-L/cc-pVTZ.

The (C₈H₆S)Fe₂(CO)₆ structures 6S-1 and 6S-2 have six terminal CO groups evenly distributed between the two iron atoms, leading to two Fe(CO)₃ moieties (Fig. 4). The Fe–C distances indicate that the thialene ligand is bonded to each Fe(CO)₃ moiety as a tetrahapto(η⁴,η⁴-C₈H₆S) ligand. This gives each iron atom has the favored 18-electron configuration.

The other (C₈H₆S)Fe₂(CO)₆ structure 6S-3 has five terminal CO groups and one bridging CO group (Fig. 4). The Fe–C distances suggest a pentahapto-trihapto (η³,η⁵-C₈H₆S) ligand (Fig. 4). In structure 6S-3, the predicted Fe⋯Fe distance of ∼3.7 Å indicates the lack of a direct iron–iron bond. Thus 6S-3 is a rather rare example of a binuclear metal carbonyl structure with a bridging CO group but no metal–metal bond. In 6S-3 each iron atom has the favored 18-electron configuration even without an iron–iron bond.

Only one low-energy (C₈H₆S)Fe₂(CO)₅ structure 5S-1 was found (Fig. 5). Other singlet as well as all triplet (C₈H₆S)Fe₂(CO)₅ structures were found to lie at least 20 kcal mol⁻¹ above 5S-1 and thus are not likely to be chemically significant. Structure 5S-1 has five terminal CO groups. The Fe–C distances in 5S-1 suggest a pentahapto-trihapto-η⁵,η³-C₈H₆S ligand. The predicted Fe–Fe distance of 2.762 Å (M06-L) in 5S-1 corresponds to a formal single bond, giving each iron atom the favored 18-electron configuration. The B3LYP method predicts a structure similar to M06-L. However, the BP86 method predicts a structure with four terminal CO groups and one bridging CO group (see ESI†).

Fig. 5 The only low-energy (C₈H₆S)Fe₂(CO)₅ structure.

Table 1 lists the theoretical harmonic ν(CO) frequencies for the (C₈H₆S)Fe₂(CO)_n (n = 6, 5) structures. The terminal ν(CO) frequencies range from 1955 to 2036 cm⁻¹, in the typical region for terminal CO groups. The six predicted ν(CO) frequencies for 6S-1 are close to the previously predicted values for lowest energy trans-(azulene)Fe₂(CO)₆ isomer, which is related to 6S-1 by substituting a –CH=CH– unit for the sulfur atom.⁹ The bridging CO group not accompanied by an iron–iron bond in 6S-3 exhibits an unusually low ν(CO) frequency of 1775 cm⁻¹. The bridging CO group in the BP86 optimized (C₈H₆S)Fe₂(CO)₅ structure 5S-1 exhibits a lower ν(CO) frequency at 1849 cm⁻¹ in accord with expectation.

Table 1 Harmonic ν(CO) vibrational frequencies (in cm⁻¹) predicted by the BP86 method for (C₈H₆S)Fe₂(CO)_n (n = 6, 5) structures. The infrared intensities (in km mol⁻¹) are in parentheses

	BP86
6S-1	1957(585), 1963(647), 1974(702), 1978(755), 2008(1915), 2029(366)
trans-(Azulene)Fe2(CO)6 (ref. 9)	1950(554), 1959(663), 1972(695), 1976(731), 2002(1891), 2027(494)
6S-2	1962(929), 1966(114), 1974(814), 1983(502), 2011(1041), 2036(738)
6S-3	1775(177), 1955(287), 1964(230), 1979(1209), 2000(1285), 2028(809)
5S-1	1849(299), 1955(151), 1971(884), 1992(1184), 2019(879)

---

3.2. C₈H₆SFe₂(CO)₄

The potential energy surface for the (C₈H₆S)Fe₂(CO)₄ system is complicated with ten structures (five singlet and five triplet structures) within 10 kcal mol⁻¹ of the global minimum 4T-1 (Fig. 6 and 7). Structure 4T-1 has one bridging CO group and three terminal CO groups and a pentahapto-trihapto-η⁵,η³-C₈H₆S ligand, as indicated by the Fe–C distances. The predicted Fe–Fe distance of 2.631 Å suggests a formal single bond, giving each iron atom in 4T-1 a 17-electron configuration corresponding to a binuclear triplet.

Fig. 6 The low-energy triplet (C₈H₆S)Fe₂(CO)₄ structures predicted by the M06-L/DZP method. The relative energies (kcal mol⁻¹) are shown in parentheses, in which the first one is from the M06-L/DZP method, and the second one is the single point energy from M06-L/cc-pVTZ.

Fig. 7 The low-energy singlet (C₈H₆S)Fe₂(CO)₄ structures predicted by the M06-L/DZP method. The energies (kcal mol⁻¹) relative to 4T-1 are shown in parentheses, in which the first one is from the M06-L/DZP method, and the second one is the single point energy from M06-L/cc-pVTZ.

The other low-energy triplet (C₈H₆S)Fe₂(CO)₄ structures 4T-2, 4T-3, 4T-4, and 4T-5 have four terminal CO groups, which are evenly distributed between the two iron atoms, leading to two Fe(CO)₂ moieties (Fig. 6). Structures 4T-2 and 4T-3 are nearly degenerate in energy with 4T-1 within 2 kcal mol⁻¹, while structures 4T-4 lies 6.4 kcal mol⁻¹ above 4T-1. Structures 4T-2, 4T-3, and 4T-4 are cis structures with both Fe(CO)₂ moieties on the same side of the thialene ligand. This allows the iron atoms to be close enough together to form formal single bonds with Fe–Fe distances ranging from 2.525 to 2.723 Å. All three (C₈H₆S)Fe₂(CO)₄ structures 4T-2, 4T-3 and 4T-4 are indicated by their Fe–C distances to have pentahapto-trihapto-η⁵,η³-C₈H₆S ligands. This gives each iron atom in these structures a 17-electron configuration for a binuclear triplet. This assumes that the iron atoms bonded to five and three carbon atoms of the thialene ligand have formal positive and negative charges, respectively. The closeness in energy of these three triplet cis-(η⁵,η³-C₈H₆S)Fe₂(CO)₄ structures suggests a fluxional system.

The (C₈H₆S)Fe₂(CO)₄ structure 4T-5, lying 5.0 kcal mol⁻¹ in energy above 4T-1, is a trans structure, in which the two Fe(CO)₂ moieties are located on opposite sides of the thialene ligand (Fig. 6). The trans geometry of 4T-5 keeps the iron atoms far enough apart to prevent direct iron–iron bonding. Instead 4T-5 has a short Fe–S distance of 2.477 Å forming an S→Fe dative bond to donate two electrons from the sulfur atom to one iron atom. Thus the thialene ligand is bonded to one iron atom as a pentahapto ligand using five carbon atoms and to the other iron atom as a tetrahapto ligand using three carbon atoms and sulfur lone-pair coordination. Each iron atom in 4T-5 thus receives five electrons from the thialene ligand, albeit in different ways. This gives each iron atom a 17-electron configuration corresponding to a binuclear triplet, even in the absence of a direct iron–iron bond.

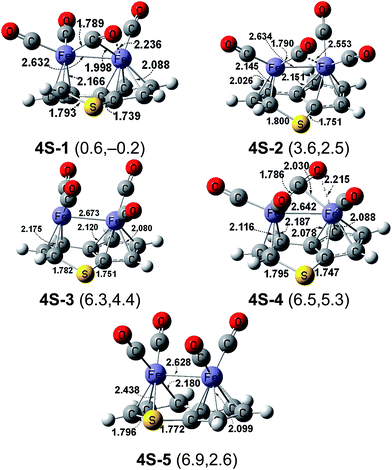
The singlet (C₈H₆S)Fe₂(CO)₄ structures 4S-1 and 4S-4 have similar geometries (Fig. 7). The former lies slightly below 4T-1 (by 0.2 kcal mol⁻¹), while the latter lies above 4T-1 by 5.3 kcal mol⁻¹. Both 4S-1 and 4S-4 have a pentahapto-trihapto-η⁵,η³-C₈H₆S ligand, one bridging η²-μ-CO group, and three terminal CO groups. They differ only in the relative positions of the terminal CO groups. The bridging η²-μ-CO groups in both 4S-1 and 4S-4 are four-electron donors, i.e., η²-μ-CO groups, as indicated by the short Fe–O distances of 2.236 Å and 2.215 Å and the corresponding unusually low ν(CO) frequencies of 1757 and 1753 cm⁻¹ (BP86), respectively. The predicted Fe–Fe distance of ∼2.63 Å in 4S-1 and 4S-4 can be interpreted as a formal single bond thereby giving each iron atom in 4S-1 and 4S-4 the favored 18-electron configuration.

The singlet (C₈H₆S)Fe₂(CO)₄ structure 4S-2, lying 2.5 kcal mol⁻¹ in energy above 4T-1, has a pentahapto-trihapto-η⁵,η³-C₈H₆S ligand, three terminal CO groups, and one semibridging CO group (Fig. 7). The semibridging group in 4S-2 has a short Fe–C distance of 1.790 Å and a long Fe–C distance of 2.553 Å. The predicted Fe→Fe distance of 2.634 Å can be interpreted as a formal dative bond from the iron atom bearing two terminal CO groups to the iron atom bearing only one terminal CO group. This interpretation gives the former iron atom the favored 18-electron configuration but the other iron atom only a 16-electron configuration.

The singlet (C₈H₆S)Fe₂(CO)₄ structures 4S-3 and 4S-5, lying 4.4 and 2.6 kcal mol⁻¹ in energy, respectively, above 4T-1, each have four terminal CO groups (Fig. 7). The predicted Fe–Fe distance of 2.673 Å in 4S-3 suggests a formal single bond to give one iron atom the favored 18-electron configuration but the other iron atom only a 16-electron configuration. The iron atom in 4S-3 with the 16-electron configuration appears to be the one with a gap in its coordination sphere trans to the Fe–Fe bond (the left iron atom in Fig. 7). Structure 4S-5 has a similar geometry to 4S-3, but the short Fe–S distance of 2.438 Å suggests an S→Fe dative bond donating two electrons from the sulfur atom to the iron atom. This leads to a bonding scheme of a pentahapto-tetrahapto thialene ligand to the central Fe₂ unit in the cis structure 4S-5 very similar to that in the trans-structure 4T-5. However, 4S-5 with its cis configuration has an Fe–Fe bonding distance of 2.628 Å in contrast to 4T-5, where the iron atoms are obviously too far apart for a direct bond. The added feature of the Fe–Fe single bond in 4S-5 combined with the donation of five electrons from the thialene ligand to each iron atom gives both iron atoms the favored 18-electron configuration.

The theoretical harmonic ν(CO) frequencies for the (C₈H₆S)Fe₂(CO)₄ structures are reported in Table 2. The ν(CO) frequencies of the terminal CO groups occur in a typical range from 1926 to 2008 cm⁻¹. As expected, the ν(CO) frequencies for the bridging CO groups are significantly lower. Thus, for the two-electron-donor bridging CO groups, the ν(CO) frequencies are 1819 cm⁻¹ in 4T-1 and 1834 cm⁻¹ in 4S-2. The ν(CO) frequencies for the four-electron-donor bridging η²-μ-CO groups in 4S-1 and 4S-4 are even lower, at 1757 and 1753 cm⁻¹ respectively.

Table 2 Harmonic ν(CO) vibrational frequencies (in cm⁻¹) predicted by the BP86 method for ten (C₈H₆S)Fe₂(CO)₄ structures. The infrared intensities (in km mol⁻¹) are in parentheses. Bridging ν(CO) frequencies are listed in bold

	BP86
4T-1	1819(361), 1956(491), 1965(1369), 2002(996)
4T-2	1932(75), 1945(946), 1962(953), 1999(1131)
4T-3	1931(84), 1945(623), 1956(1292), 2005(1133)
4T-4	1926(34), 1942(941), 1955(1189), 1996(1119)
4T-5	1941(563), 1943(1074), 1980(2418), 1995(12)
4S-1	1757(362), 1950(249), 1963(1103), 2004(1059)
4S-2	1834(292), 1951(921), 1962(824), 2005(981)
4S-3	1927(156), 1955(584), 1961(1046), 2006(1083)
4S-4	1753(382), 1948(286), 1963(1144),2008(925)
4S-5	1933(5), 1953(1122), 1961(685), 2003(1159)

---

3.3. Thermochemistry

Table 3 shows the CO dissociation energies for the reactions (C₈H₆S)Fe₂(CO)_n → (C₈H₆S)Fe₂(CO)_n−1 + CO (n = 6, 5) based on the lowest-energy structures. The dissociation energy for the loss of one CO group from (C₈H₆S)Fe₂(CO)₆ (6S-1) to give (C₈H₆S)Fe₂(CO)₅ (5S-1) is 9.3 kcal mol⁻¹ (M06-L/cc-pVTZ), while that for the loss of one CO group from (C₈H₆S)Fe₂(CO)₅ (5S-1) to give (C₈H₆S)Fe₂(CO)₅ (4T-1) is much larger at 40.3 kcal mol⁻¹. The latter is comparable with the typical range for metal carbonyl derivatives, as suggested by the experimental dissociation energies for Ni(CO)₄, Fe(CO)₅, and Cr(CO)₆ of 27, 41, and 37 kcal mol⁻¹, respectively.³¹ However, the relatively low dissociation energy of (C₈H₆S)Fe₂(CO)₆ to give (C₈H₆S)Fe₂(CO)₅ of 9.3 kcal mol⁻¹ suggests facile formation of the pentacarbonyl rather than the hexacarbonyl from thermal reactions of thialene with iron carbonyls. This may relate to the energy released by forming an Fe–Fe bond in going from (C₈H₆S)Fe₂(CO)₆ to give (C₈H₆S)Fe₂(CO)₅.

Table 3 Energies (kcal mol⁻¹) for dissociation of a carbonyl group from the C₈H₆SFe₂(CO)_n (n = 6, 5) derivatives and the disproportionation energy for C₈H₆SFe₂(CO)₅ based on the lowest-energy structures predicted by the M06-L/DZP methods. Those refined using the M06-L/cc-pVTZ single point energies are also listed

Reaction	DZP	cc-pVTZ
(C8H6S)Fe2(CO)6 (6S-1) → (C8H6S)Fe2(CO)5 (5S-1) + CO	11.5	9.3
(C8H6S)Fe2(CO)5 (5S-1) → (C8H6S)Fe2(CO)4 (4T-1) + CO	42.1	40.3
2(C8H6S)Fe2(CO)5 (5S-1) → (C8H6S)Fe2(CO)6 (6S-1) + (C8H6S)Fe2(CO)4 (4T-1)	30.6	31.1

---

Table 3 also gives the energy of the disproportionation reaction 2(C₈H₆S)Fe₂(CO)₅ (5S-1) → (C₈H₆S)Fe₂(CO)₆ (6S-1) + (C₈H₆S)Fe₂(CO)₄ (4T-1), based on the lowest-energy structures. The disproportionation energy predicted by the M06-L method for 5S-1 is substantially endothermic at 31.1 kcal mol⁻¹. Both the dissociation and disproportionation energies suggest that the lowest energy (C₈H₆S)Fe₂(CO)₅ derivative 5S-1 is viable and a likely product from reactions of thialene with iron carbonyls.

3.4. NBO analysis of the Fe–Fe bonds

Table 4 reports the Wiberg bond indices (WBIs) and the bond distances for the iron–iron bond in the singlet (C₈H₆S)Fe₂(CO)_n (n = 6, 5, 4) derivatives determined by NBO analysis³² using the M06-L method. Results are not included for the triplet structures, since the WBI values are a less reliable indicator of metal–metal bond orders in higher spin state structures. The WBI values are consistent with the formal Fe–Fe bond orders based on the iron–iron distances and electron counting. For the formal iron–iron single bonds, the WBIs range from 0.32 to 0.37 except for 4S-3 with an abnormally high WBI of 0.55 for a formal iron–iron single bond. This abnormally high WBI may relate to the 16-electron configuration of one of the iron atoms in 4S-3. The C₈H₆SFe₂(CO)₆ structures having Fe⋯Fe distances clearly too long for a direct bond have much lower WBIs ranging from 0.04 to 0.10.

Table 4 The Fe–Fe distances (in Å), the Fe–Fe Wiberg bond indices (WBI), and the natural atomic charges on the Fe atoms (Q_Fe) for the singlet (C₈H₆S)Fe₂(CO)_n structures predicted by the M06-L method

	Fe–Fe, distance	Formal Fe–Fe, bond order	WBIs	QFe
6S-1	—	0	0.09	−1.48/−1.53
6S-2	4.103	0	0.04	−1.52/−1.55
6S-3	3.662	0	0.10	−1.17/−1.52
5S-1	2.762	1	0.32	−1.02/−1.36
4S-1	2.632	1	0.37	−0.52/−1.36
4S-2	2.634	1	0.33	−1.14/−0.49
4S-3	2.673	1	0.55	−0.97/−0.63
4S-4	2.642	1	0.34	−0.52/−1.33
4S-5	2.628	1	0.37	−0.92/−1.01

---

The natural charges on the iron atoms predicted by the M06-L method are also reported in Table 4. In general, a larger number of CO groups bonded to an iron atom leads to a more negative natural charge. In this connection, the iron atoms bonded to three CO groups in 6S-1, 6S-2, and 6S-3 have negative natural charges ranging from −1.48 to −1.55, and that in 5S-1 has a negative natural charge of −1.36. The iron atom bonded to 2½ CO groups in 6S-3 (i.e., two terminal CO groups and one bridging CO group) has a natural charge of −1.17. The iron atoms bonded to two carbonyl groups in 5S-1, 4S-3, and 4S-5 have natural charges ranging from −0.92 to −1.02. These observations of natural charge confirm the favored 18-electron configuration for the iron atom. The iron atom with a 16-electron configuration in 4S-3 with an obviously vacant coordination site (the “left” iron atom in Fig. 6) has a less negative natural charge than would be expected for an iron atom bearing two CO groups, namely −0.63 rather than −0.9 to −1.0. The presence of a four-electron donor η²-μ-CO group makes the natural charge on the iron atom directly bonded to the oxygen atom significantly less negative, e.g., around −0.5 in 4S-1 and 4S-4, both of which have this structural feature. These significantly negative natural charges on all of the iron atoms in the (thialene)Fe₂(CO)_n complexes discussed in this paper imply that the π-back-bonding of a carbonyl group, although strong compared with that of most other ligands in inorganic chemistry, is not strong enough to remove all of the negative charge introduced by the forward σ bonding.

4. Discussion

Previous experimental^33,34 and theoretical³⁵ studies suggest that reactions of benzothiophene with iron carbonyls lead to insertion of iron into a carbon–sulfur bond to give a (C₈H₆S)Fe₂(CO)₆ complex having a ferrathianaphthalene structure containing a six-membered FeSC₄ ring system bonded to an exocyclic Fe(CO)₃ group as a tetrahapto ligand with an Fe–Fe bond as well as an Fe–S bond and two Fe–C bonds (Fig. 1). None of the six carbon atoms in the benzene ring of benzothiophene are within bonding distance of the (C₈H₆S)Fe₂(CO)₆ complex derived from benzothiophene in this manner. By contrast, the isomeric lowest-energy (C₈H₆S)Fe₂(CO)₆ derivative 6S-1 derived from thialene (Fig. 4) retains the thialene bicyclic structure with no iron insertion into a C–S bond. Thus in 6S-1 thialene bonds to each Fe(CO)₃ moiety as a tetrahapto ligand similar to butadiene in the butadiene-iron tricarbonyl^36–38 (η⁴-C₄H₆)Fe(CO)₃. In this way all eight thialene carbon atoms in 6S-1 are within bonding distance of one of the iron atoms, whereas the sulfur atom is not within bonding distance of either iron atom. In fact the next two higher energy (thialene)Fe₂(CO)₆ structures 6S-2 and 6S-3, like 6S-1, also have distinct 1,3-diene subunits of the thialene ligand coordinating to each Fe(CO)₃ moiety without involvement of the sulfur atom. The Fe(CO)₃ units in 6S-1 are located on opposite sides of the thialene ligand so that there is no iron–iron bond. Even the higher energy (thialene)Fe₂(CO)₆ structures 6S-2 and 6S-3, with both Fe(CO)₃ moieties on the same side of the thialene ligand, have the ligand bent enough so that the two iron atoms are too far apart to form a direct iron–iron bond. Nevertheless 6S-3 has a bridging CO group even though it lacks a direct iron–iron bond (Fig. 4). Such bridging CO groups not supported by a metal–metal bond are rare in metal carbonyl chemistry. An iron–iron bond is not needed to hold the two halves of 6S-3 together since both iron atoms are bonded to the same thialene ligand. The bridging CO group in 6S-3 not supported by an Fe–Fe bond has a significantly lower ν(CO) frequency than comparable bridging CO groups supported by Fe–Fe bonds.

The difference between the (C₈H₆S)Fe₂(CO)₆ complexes derived from benzothiophene (Fig. 1) and thialene (Fig. 4) appears to arise from the location of the sulfur atom in a five-membered ring in benzothiophene but in a six-membered ring in thialene. A smaller five-membered ring containing a sulfur atom would be expected to be more susceptible towards C–S bond cleavage than a six-membered ring containing a sulfur atom, because of increased ring strain. The (thialene)Fe₂(CO)₆ structure 6S-1 appears to be reasonably favorable, since the next lowest energy (thialene)Fe₂(CO)₆ structure 6S-2 lies ∼10 kcal mol⁻¹ in energy above 6S-1 (Fig. 4).

The predicted CO dissociation energy of (thialene)Fe₂(CO)₆ to (thialene)Fe₂(CO)₅ of ∼9 kcal mol⁻¹ is rather low for a metal carbonyl derivative using the experimental CO dissociation energies of the simple mononuclear carbonyls Cr(CO)₆, Fe(CO)₅, and Ni(CO)₄ of 27, 41, and 37 kcal mol⁻¹, respectively,³¹ as reference points. This suggests that the favored binuclear thialene iron carbonyl might be the pentacarbonyl (thialene)Fe₂(CO)₅. However, only one low-energy structure, namely 5S-1, was found for (thialene)Fe₂(CO)₅ (Fig. 5). Structure 5S-1 is derived from the lowest energy (azulene)Fe₂(CO)₅ structure (Fig. 3) by replacing the uncomplexed C=C double bond with a sulfur atom similar to the generation of the thiophene structure from benzene. Structure 5S-1 thus has a pentahapto-trihapto thialene ligand, exclusively terminal CO groups, and an Fe–Fe distance of ∼2.76 Å suggesting a formal single bond. This Fe–Fe distance in the (thialene)Fe₂(CO)₅ structure 5S-1 is comparable to the experimental Fe–Fe distance of 2.782 Å in (azulene)Fe₂(CO)₅.⁸

The complicated energy surface of the unsaturated (thialene)Fe₂(CO)₄ system contains five triplet structures and five singlet structures within ∼6 kcal mol⁻¹ of the lowest energy structure. The triplet and singlet structures are thus of comparable energies. All of these (thialene)Fe₂(CO)₄ structures except for the triplet structure 4T-5 (at 5.0 kcal mol⁻¹ above the lowest energy structure 4T-1) have the cis configuration with both iron atoms on the same side of the thialene ligand to allow for the possibility of direct iron–iron bonding. The lowest energy triplet (thialene)Fe₂(CO)₄ structures can be derived by removal of a CO group from the Fe(CO)₃ moiety of the (thialene)Fe₂(CO)₅ structure. The Fe–Fe distance changes relatively little during this CO removal process, suggesting retention of the single bond rather than major shortening to a formal double bond. Retaining the formal single bond in (thialene)Fe₂(CO)₄ gives each iron atom the 17-electron configuration for a binuclear triplet.

A singlet electronic state (thialene)Fe₂(CO)₄ requires an Fe=Fe double bond for each iron atom to have the favored 18-electron configuration. However, reduction of the Fe–Fe distance from ∼2.76 Å only to ∼2.63 Å is hardly sufficient to convert a formal single bond to a formal double bond. In any case one of the CO groups in each of the two low-energy singlet (thialene)Fe₂(CO)₄ structures 4S-1 and 4S-4 is a four-electron donor bridging η²-μ-CO group with a bonding Fe–O distance of ∼2.22 Å to one of the iron atoms. In such structures a formal Fe–Fe single bond combined with the typical pentahapto-trihapto bonding of the thialene ligand found in most (thialene)Fe₂(CO)_n (n = 5, 4) structures is sufficient to give each iron atom the favored 18-electron configuration. The singlet structures 4S-2 and 4S-3 have only two-electron donor CO groups so that only one iron atom can have the favored 18-electron configuration with the formal Fe–Fe bond. The other iron atom must necessarily have a 16-electron configuration.

In all of the (thialene)Fe₂(CO)_n (n = 6, 5, 4) structures discussed so far, the Fe⋯S distance is too long to suggest any participation of the sulfur lone pair in the ligand–metal bonding. The single structure with a direct Fe–S interaction indicated by a short Fe–S distance of ∼2.44 Å is the singlet (thialene)Fe₂(CO)₄ structure 4S-5, lying ∼3 kcal mol⁻¹ above 4T-1. Adding the sulfur lone pair to the single π electron on each of the eight thialene carbon atoms makes the η⁵,η⁴-thialene ligand in 4S-5 a 10-electron donor to the central Fe₂ unit. Dividing these ten electrons equally between the two iron atoms combined with the Fe–Fe bond gives both iron atoms in 4S-5 the favored 18-electron configuration.

Conspicuously absent among this plethora of (thialene)Fe₂(CO)₄ structures are low-energy singlet structures with short enough Fe=Fe distances to correspond clearly to the formal double bonds required to give each iron atom the favored 18-electron configuration. Instead the low-energy singlet (thialene)Fe₂(CO)_n structures have either a single four-electron bridging η²-μ-CO group (4S-1 and 4S-4 in Fig. 7), participation of the sulfur lone pair in the thialene–metal bonding (4S-5), or a 16-electron configuration for one of the iron atoms (4S-2 and 4S-3). This contrasts with the (azulene)Fe₂(CO)₄ system in which the lowest energy structure optimized by BP86 has all two-electron donor CO groups and a short Fe=Fe distance of ∼2.48 Å suggesting a formal double bond.⁹

5. Summary

Thialene (C₈H₆S) is an isomer of benzothiophene related to azulene by replacement of a C=C unit in the seven-membered ring by a sulfur atom. The geometries of binuclear iron carbonyl complexes of thialene (C₈H₆S)Fe₂(CO)_n (n = 6, 5, 4) have been investigated by density functional theory. The lowest energy (thialene)Fe₂(CO)₆ structures have a bis(tetrahapto)-η⁴,η⁴-thialene ligand bonded to two separate Fe(CO)₃ units without involvement of the sulfur atom. This differs from the isomeric (benzothiophene)Fe₂(CO)₆ structure known experimentally in which an iron atom has inserted into a carbon–sulfur bond to give a ferrathianaphthalene system. The only low-energy (thialene)Fe₂(CO)₅ structure has a pentahapto-trihapto-η⁵,η³-thialene ligand bonded to an Fe₂(CO)₅ unit, again without involvement of the sulfur atom. This structure is related to the experimental structure of azulene diiron pentacarbonyl, (η⁵,η³-C₁₀H₈)Fe₂(CO)₅ by replacement of the uncomplexed C=C double bond in the seven-membered ring with a sulfur atom. The potential energy surface of the unsaturated (thialene)Fe₂(CO)₄ is very complicated but does not include any low-energy structures with formal Fe=Fe double bonds. Instead triplet structures are found having pentahapto-trihapto-η⁵,η³-thialene ligands and formal Fe–Fe single bonds. Low-energy singlet (thialene)Fe₂(CO)₄ structures have four-electron donor η²-μ-CO groups. A higher-energy (thialene)Fe₂(CO)₄ structure (4S-5) ∼3 kcal mol⁻¹ above the global minimum provides the only example of a (thialene)Fe₂(CO)_n complex encountered in this work where the thialene sulfur atom as well as the eight carbon atoms are involved in bonding to the central Fe₂ system.

Thialene iron carbonyls have not yet been synthesized. Thermochemical considerations (Table 3) suggest (η⁵,η³-thialene)Fe₂(CO)₅ (i.e., 5S-1 in Fig. 5) analogous to (η⁵,η³-azulene)Fe₂(CO)₅ (Fig. 3) as a realistic synthetic objective. This thialene iron carbonyl complex is potentially accessible from the reaction of thialene with Fe₂(CO)₉ under mild conditions. Alternatively, the use of (benzalacetone)Fe(CO)₃ as a generator of Fe(CO)₃ fragments under mild conditions³⁹ might provide an alternative reagent for binding iron carbonyl fragments to thialene.

Acknowledgements

This research was supported by Funds for Sichuan Distinguished Scientists (Grant No. 2015JQ0042 – China), Funds for the Youth Innovation Team of the Education Department of Sichuan Province (Grant No. 14TD0013 – China), the National Natural Science Foundation of China (Grant No. 11174236) and the U.S. National Science Foundation (Grant CHE-1361178).

References

1. R. J. Angelici, in Encyclopedia of Inorganic Chemistry, ed. R. B. King, 2nd edn, Wiley, 2005, pp. 1860–1877.
2. H. D. Kaesz, R. B. King, T. A. Manuel, L. D. Nichols and F. G. A. Stone, J. Am. Chem. Soc., 1960, 82, 4749.
3. R. B. King and F. G. A. Stone, J. Am. Chem. Soc., 1960, 82, 4557.
4. A. E. Ogilvy, M. Draganjac, T. B. Rauchfuss and S. R. Wilson, Organometallics, 1988, 7, 1171.
5. R. F. X. Klein and V. Horak, J. Org. Chem., 1986, 51, 4644.
6. R. Burton and G. Wilkinson, Chem. Ind., 1958, 1205.
7. M. R. Churchill and P. H. Bird, Chem. Commun., 1967, 746.
8. M. R. Churchill, Inorg. Chem., 1967, 6, 190.
9. H. Wang, Z. Sun, Y. Xie, R. B. King and H. F. Schaefer, Organometallics, 2010, 29, 630.
10. M. Brynda, L. Gagliardi, P. O. Widmark, P. P. Power and B. O. Roos, Angew. Chem., Int. Ed., 2006, 45, 3804.
11. N. Sieffert and M. Buhl, J. Am. Chem. Soc., 2010, 132, 8056.
12. P. Schyman, W. Lai, H. Chen, Y. Wang and S. Shaik, J. Am. Chem. Soc., 2011, 133, 7977.
13. R. D. Adams, W. C. Pearl, Y. O. Wong, Q. Zhang, M. B. Hall and J. R. Walensky, J. Am. Chem. Soc., 2011, 133, 12994.
14. R. Lonsdale, J. Olah, A. J. Mulholland and J. N. Harvey, J. Am. Chem. Soc., 2011, 133, 15464.
15. L. Crawford, D. J. Cole-Hamilton, E. Drent and M. Bühl, Chem.–Eur. J., 2014, 20, 13923.
16. H. Zhekova, M. Krykunov, J. Autschbach and T. Ziegler, J. Chem. Theory Comput., 2014, 10, 3299.
17. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
18. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
19. A. D. Becke, Phys. Rev. A, 1988, 38, 3098.
20. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822.
21. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
22. Y. Zeng, S. Wang, H. Feng, Y. Xie and R. B. King, Int. J. Mol. Sci., 2011, 12, 2216.
23. S. Huzinaga, J. Chem. Phys., 1965, 42, 1293.
24. T. H. Dunning, J. Chem. Phys., 1970, 53, 2823.
25. T. H. Dunning and P. J. Hay, in Methods of Electronic Structure Theory, ed. H. F. Schaefer, Plenum, New York, 1977, pp. 1–27.
26. A. J. H. Wachters, J. Chem. Phys., 1970, 52, 1033.
27. D. M. Hood, R. M. Pitzer and H. F. Schaefer, J. Chem. Phys., 1979, 71, 705.
28. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007; D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358.
29. N. B. Balabanov and K. A. Peterson, J. Chem. Phys., 2005, 123, 064107.
30. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009.
31. L. S. Sunderlin, D. Wang and R. R. Squires, J. Am. Chem. Soc., 1993, 115, 12060.
32. F. Weinhold and C. R. Landis, Valency and Bonding: A Natural Bond Order Donor–Acceptor Perspective, Cambridge University Press, Cambridge, England, U. K., 2005, pp. 32–36.
33. R. B. King and F. G. A. Stone, J. Am. Chem. Soc., 1960, 82, 4557.
34. A. E. Ogilvy, M. Draganjac, T. B. Rauchfuss and S. R. Wilson, Organometallics, 1988, 7, 1171.
35. R. Jin, X. Chen, Q. Du, H. Feng, Y. Xie, R. B. King and H. F. Schaefer, New J. Chem., 2015, 39, 7040.
36. O. Reihlen, A. Gruhl, G. Hessling and O. Pfrengle, Liebigs Ann. Chem., 1930, 482, 161.
37. B. F. Hallam and P. L. Pauson, J. Chem. Soc., 1958, 642.
38. O. S. Mills and G. Robinson, Acta Crystallogr., 1963, 16, 758.
39. R. B. King and M. N. Ackerman, J. Organomet. Chem., 1973, 60, C57–C59.

---

Footnote

† Electronic supplementary information (ESI) available: Tables S1–S4: harmonic vibrational frequencies (in cm⁻¹) and infrared intensities (in parentheses, in km mol⁻¹) for the (thialene)Fe₂(CO)_n (n = 6, 5) structures 6S-1, 6S-2, 6S-3, and 5S-1; Tables S5–S9: harmonic vibrational frequencies (in cm⁻¹) and infrared intensities (in parentheses, in km mol⁻¹) for the (thialene)Fe₂(CO)₄ structures 4T-n (n = 1–5); Tables S10–S14: harmonic vibrational frequencies (in cm⁻¹) and infrared intensities (in parentheses, in km mol⁻¹) for the (thialene)Fe₂(CO)₄ structures 4S-n (n = 1–5); Tables S15–S18: Cartesian coordinates and total energies for the (thialene)Fe₂(CO)_n (n = 6, 5) structures 6S-n (n = 1–3) and 5S-1; Tables S19–S23: Cartesian coordinates and total energies for the (thialene)Fe₂(CO)₄ structures 4T-n (n = 1–5); Tables S24–S28: Cartesian coordinates and total energies for the (thialene)Fe₂(CO)₄ structures 4S-n (n = 1–5); Table S29: total energies (E, in hartree), relative energies (E, in kcal mol⁻¹), and Fe–Fe and S–Fe distances (in Å) for the (thialene)Fe₂(CO)₆ and (thialene)Fe₂(CO)₅ structures 6S-n (n = 1–3) and 5S-1; Table S30: total energies (E, in hartree), relative energies (E, in kcal mol⁻¹), and Fe–Fe and S–Fe distances (in Å) for the (thialene)Fe₂(CO)₄ structures 4T-n (n = 1–5); Table S31: total energies (E, in hartree), relative energies (E, in kcal mol⁻¹), and Fe–Fe and S–Fe distances (in Å) for the (thialene)Fe₂(CO)₄ structures 4S-n (n = 1–5); Table S32: harmonic ν(CO) vibrational frequencies (in cm⁻¹) predicted by the BP86 method for (thialene)Fe₂(CO)_n (n = 6, 5) structures; Table S33: harmonic ν(CO) vibrational frequencies (in cm⁻¹) predicted by the BP86 method for (C₈H₆S)Fe₂(CO)₄ structures; Fig. S1: the (thialene)Fe₂(CO)₆ structures 6S-n (n = 1 to 3); Fig. S2: the (thialene)Fe₂(CO)₅ structure 5S-1; Fig. S3: the triplet (thialene)Fe₂(CO)₄ structures 4T-n (n = 1 to 5); Fig. S4: the singlet (thialene)Fe₂(CO)₄ structures 4S-n (n = 1 to 5); complete Gaussian reference. See DOI: 10.1039/c6ra14458f

---