A polysulfobetaine hydrogel for immobilization of a glucose-binding protein
Peter Kasák†
*a,
Jaroslav Mosnáčekb,
Martin Dankob,
Igor Krupa†a,
Gabriela Hlouškováb,
Dušan Chorvátc,
Marina Koukakid,
Spyridoula Karamanoue,
Anastassios Economoude and
Igor Lacík*b
aCenter for Advanced Materials, Qatar University, 2713 Doha, Qatar. E-mail: peter.kasak@qu.edu.qa
bPolymer Institute of the Slovak Academy of Sciences, Dúbravská cesta 9, 845 41 Bratislava, Slovakia. E-mail: igor.lacik@savba.sk
cInternational Laser Center, Ilkovičova 3, 841 04 Bratislava, Slovakia
dIMBB-FoRTH, 71110 Iraklio, Crete, Greece
eKU Leuven, Department of Microbiology and Immunology, Rega Institute for Medical Research, Laboratory of Molecular Bacteriology, B-3000 Leuven, Belgium
First published on 31st August 2016
Abstract
A hydrogel based on sulfobetaine methacrylate monomer N-(methacryloyloxyethyl)-N,N-dimethyl-N-(3-sulfopropyl)ammonium betaine and N,N-bis(methacryloyloxyethyl)-N-methyl-N-(3-sulfopropyl)ammonium betaine used as a crosslinker was investigated as a potential material for biosensor applications. The glucose diffusion coefficient of 1.2 × 10−10 m2 s−1 was determined from the glucose release experiment. Inverse size-exclusion chromatography was performed to determine the molecular weight cut-off of the hydrogel to be 8 kDa with respect to pullulans that corresponds to a viscosity radius of 2.1 nm. The narrow pore-size distribution suggests that using the sulfobetaine crosslinker suppresses the composition drift and results in a homogeneous hydrogel network. Furthermore, a glucose biosensor construct comprising the periplasmic glucose-binding protein of Escherichia coli fused to cyan and yellow fluorescent proteins was effectively entrapped in the hydrogel exhibiting no leakage for at least 7 days. The glucose-binding protein showed stability of its secondary structure and sensitivity to glucose as assessed by circular dichroism and Förster (fluorescence) resonance energy transfer measurements under physiological conditions and a physiological range of glucose concentration, respectively.
1. Introduction
Prevalence of the health deterioration resulting from diabetes calls for urgent attention to easily accessible and precise monitoring of blood glucose levels in diabetic patients. Current analytical methods for direct glucose detection include electrochemical impedance spectroscopy,1 amperometry,2 liquid chromatography,3 polarimetry,4 and capillary electrophoresis.5 Personal glucometers utilize the reaction between glucose and glucose oxidase, the principle behind the electrochemical amperometric sensor.6–8 In some cases, small molecules of molar mass similar to that of glucose but easily detectable, preferably by UV/vis spectroscopy, are used instead of direct glucose detection.9,10 A typical substitute for glucose is its fluorescently labelled derivative that is detected by confocal laser scanning microscopy (CLSM) or fluorimetry.11Hydrogel polymer networks are employed in several applications related to biology, biotechnology, bioelectronics and medicine12–17 due to their ability to immobilize various biological species in a non-destructive manner. The immobilization of enzymes and proteins in hydrogels is frequently used in biosensors which allow for localization of entrapped sensor species and improvement of their performance, selectivity and stabilization.18–22 The hydrogel properties need to be tailored in such manner as to prevent malfunction and leakage of sensoric proteins, but without hindering their sensing functions. At the same time, an understanding of the diffusion of the solute of interest within the hydrogel and the permeation properties of the hydrogel is essential for the optimal functional immobilization.
Immobilization of proteins was carried out in various types of natural (e.g. hyaluronic and alginic acid, chitosan) and synthetic (e.g. poly(ethylene glycol), poly(lactic acid), poly(N-vinylpyrrolidone), poly(hydroxyethyl methacrylate)) hydrogel polymer networks and in sol–gel processes.23,24 Sulfobetaine-based hydrogels were identified as an appropriate material to satisfy several required properties for immobilization of biological species. They are highly ionic and exhibit a low biofouling character, which makes them suitable for designing non-biofouling25 and blood compatible materials26 or surfaces appropriate for implants.27–29 These properties result from the unique nature of sulfobetaines that are inner salts of positive ammonium and negative sulphate groups on different atoms in a monomer molecule with overall neutral charge.30,31 Physical and mechanical properties of hydrogels prepared from sulfobetaine polymers can be modulated by changing the monomer concentration.32 A crucial role is also played by the type and content of the crosslinker. It is recommended to use crosslinkers with chemical structures similar to the structure of the monomer to prevent composition drift that results in lowering the mechanical properties due to an increased heterogeneity of hydrogel network.33
Fluorescence protein biosensors based on Förster (fluorescence) resonance energy transfer (FRET) coupled with measurement of glucose concentration34 is one of the most commonly used approaches for detection. The protein constructs such as glucose/galactose-binding protein and its genetically engineered modifications have been applied for this purpose.19,35,36 An advantage of using these protein constructs is in their complete reversibility, fairly simple application, and independence on oxygen concentration and pH. However, most of those systems were used in solution34,37,38 and by chemical immobilization on optical fibre,39,40 hydrogel41 or beads.42 Physical immobilization is rare and is limited to entrapment within a dialysis membrane.43
Due to our interest in development and construction of an implantable glucose biosensor44,45 based on a hydrogel waveguide containing an entrapped glucose-sensitive protein,46 we developed a sulfobetaine hydrogel matrix for physical entrapment of genetically engineered glucose biosensor construct (GBPfluo5). Moreover, while the non-biofouling character of zwitterionic sulfobetaine hydrogels is well documented,32,47 the information on glucose diffusion and permeability in this type of material is, to our knowledge, scarce. These are essential hydrogel characteristics since the glucose diffusion is the limiting step for sensing the glucose level in the environment of sensing protein. This was the reason why in this work we focused on determination of these hydrogel characteristics. The diffusion coefficient was determined by measuring the glucose release from the sulfobetaine-based hydrogel employing a clinical analytical glucometer. The molecular weight cut-off and pore-size distribution were determined by means of an inverse size-exclusion chromatography. Hydrogels based on N-(2-methacryloyloxyethyl)-N,N-dimethyl-N-(3-sulfopropyl)ammonium betaine (SBDMA) monomer and N,N-bis(2-methacryloyloxyethyl)-N-methyl-N-(3-sulfopropyl)ammonium betaine (CL1) crosslinker33 were prepared by free radical polymerization in the absence (polySBDMA) and in the presence of glucose biosensor construct, GBP-Fluo5, used as a sensoric protein (polySBDMA-GBPfluo-5) (Scheme 1). Stability, long term performance in sensing the glucose levels and leaching of the GBP-Fluo5 protein from hydrogel were tested.
2. Experimental
Materials and reagents
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm). GBP-Fluo5 was purified from the cell lysate supernatant by Ni2+–NTA (Qiagen) affinity chromatography. The resin was washed once with a high-salt solution (1 M NaCl, 50 mM Tris–HCl pH 8.0, 5 mM imidazole, 10% glycerol) and once with a low-salt solution (50 mM NaCl, 50 mM Tris–HCl pH 8.0, 5 mM imidazole, 10% glycerol) and the protein was eluted with 150 mM imidazole solution. Protein was dialyzed for 12 hours at 4 °C in AIF in the presence of 50% glycerol v/v and was stored at −80 °C.
000 rpm). GBP-Fluo5 was purified from the cell lysate supernatant by Ni2+–NTA (Qiagen) affinity chromatography. The resin was washed once with a high-salt solution (1 M NaCl, 50 mM Tris–HCl pH 8.0, 5 mM imidazole, 10% glycerol) and once with a low-salt solution (50 mM NaCl, 50 mM Tris–HCl pH 8.0, 5 mM imidazole, 10% glycerol) and the protein was eluted with 150 mM imidazole solution. Protein was dialyzed for 12 hours at 4 °C in AIF in the presence of 50% glycerol v/v and was stored at −80 °C.Formation of polySBDMA and polySBDMA-GBP-Fluo5 hydrogels
The polySBDMA hydrogels were prepared according to the protocol described recently.33 SBDMA aqueous solution (2.0 M, 1 mL), crosslinker CL1 (1 mol% to SBDMA) and 40 μL per 1 mL of 0.22 M APS aqueous solution (final APS concentration equals 8.8 mM) were placed in a vial. The solution was purged with argon and stirred for 30 min to ensure that oxygen is removed and all the components are dissolved. In the case of polySBDMA hydrogel, a 14 μL aliquot per 1 mL (0.093 M) of TMEDA (the accelerator) was added and stirred for an additional 30 seconds. The solution was inserted between two glass plates with a glass spacer (dimensions ∼ L × W × T = 55 × 20 × 2 mm) and closed with a paraffin film. After a polymerization process at 23 ± 1 °C polySBDMA hydrogel slabs were immersed and stored in ultrapure water for further characterization.In the case of polySBDMA-GBPfluo-5 hydrogel, the process of hydrogel formation was identical apart from using PBS buffer as the solvent instead of water to dissolve all the components. After addition of TMEDA, GBP-Fluo5 and BSA solutions were added in the amount to provide final concentration in a hydrogel of 1 × 10−5 M GBP-Fluo5 and 0.45 × 10−3 M BSA and stirred for 30 seconds. For perfusion tests, samples in the shape of cylinders (diameter of 1 mm, length of 15 mm) were prepared by insertion of the solution into a sterile catheter BBraun Vasofix® Safety 20 G Pink. The inserting side was sealed gently with a stopper and the opposite catheter end was protected by sterile rubber. After a polymerization process at 23 ± 1 °C, polySBDMA-GBP-Fluo5 hydrogels were immersed and stored in PBS for further characterization.
Determination of glucose diffusion coefficient
PolySBDMA hydrogel with dimensions of 20 × 20 × 2 mm was saturated by glucose by immersion of hydrogel in 300 mM glucose solution for 12 hours. The hydrogel was positioned onto a custom-made stand with four needles fixing the hydrogel in its position and allowing for an exposure of the entire surface by the surrounding solution placed in a 25 mL beaker and covered by 10 mL of ultrapure water, which was constantly stirred by a magnetic stirrer. In the selected periods of time between 1 to 120 min, the entire solution with the released glucose was removed and replaced by another 10 mL of ultrapure water with zero glucose concentration. This protocol was selected in order to keep the boundary conditions as close as possible to the applied model (described below). The concentration of released glucose from the hydrogel to water was analyzed in water using a commercial glucose analyzer (HITACHI 917, Roche) at a hospital certified laboratory. The measurements were performed on five replicates.Molecular weight cut-off and pore-size distribution
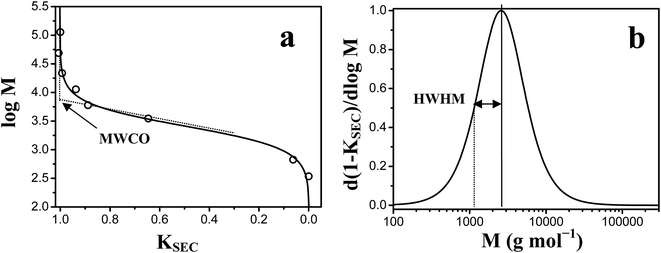
The molecular weight cut-off (MWCO) of polySBDMA hydrogels was determined by using inverse size-exclusion chromatography (ISEC) following the principles developed for characterization of hydrogel microcapsules.51,52 Narrow dispersity pullulan standards (Polymer Laboratories, Ltd., UK) of the average molecular weights in the range between 667 and 113![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da and saccharose (342 Da) were injected onto a glass column 10 × 50 mm (Omnifit, UK), fitted with two adjustable plungers. The column was filled with 4 mL of polySBDMA hydrogel pieces of around 1 mm3 in size, which were obtained by pressing the hydrogel slabs through the stainless steel sieve. The column was attached to a Waters SEC set-up consisting of a Waters 515 pump, Rheodyne Injector 7725i with 100 μL loop and Waters 2410 DRI detector. 0.9 wt% NaCl was used as an eluent at a flow rate of 0.03 mL min−1. The ISEC set-up run at the room temperature was equilibrated for 24 hours until a stable baseline was obtained. WinGPC®7.2 software (Polymer Standards Service, Mainz, Germany) was used for data acquisition and evaluation. The data evaluation of these characteristics was based on determination of the partition coefficient KSEC of different pullulan standards injected on the column formed by the hydrogel following the work of Brissova et al.51,52 The chromatographic partition coefficient KSEC for each ith pullulan standard was determined from eqn (1):
000 Da and saccharose (342 Da) were injected onto a glass column 10 × 50 mm (Omnifit, UK), fitted with two adjustable plungers. The column was filled with 4 mL of polySBDMA hydrogel pieces of around 1 mm3 in size, which were obtained by pressing the hydrogel slabs through the stainless steel sieve. The column was attached to a Waters SEC set-up consisting of a Waters 515 pump, Rheodyne Injector 7725i with 100 μL loop and Waters 2410 DRI detector. 0.9 wt% NaCl was used as an eluent at a flow rate of 0.03 mL min−1. The ISEC set-up run at the room temperature was equilibrated for 24 hours until a stable baseline was obtained. WinGPC®7.2 software (Polymer Standards Service, Mainz, Germany) was used for data acquisition and evaluation. The data evaluation of these characteristics was based on determination of the partition coefficient KSEC of different pullulan standards injected on the column formed by the hydrogel following the work of Brissova et al.51,52 The chromatographic partition coefficient KSEC for each ith pullulan standard was determined from eqn (1):| KSEC = (Vi − Vt)/(V0 − Vt), | (1) |
Mechanical properties
Mechanical properties of the hydrogels were tested using a Texture Analyzer TA-XT2i (Stable Micro Systems, Godalming, UK) equipped with a force transducer of 1 mN resolution and Texture Expert software version 1.16 used for data acquisition and evaluation. The mechanical stability was measured on hydrogel cylinders of 3.83 mm diameter and 1 mm thickness in compression mode using a vertically moving mobile probe of 4 mm diameter at a constant speed of 0.5 mm s−1. The cylinders were deformed up to about 90% of their initial height with the force displacement data recorded at a frequency of 100 Hz. The force (expressed in grams) exerted by the probe on the hydrogel was recorded as a function of the displacement. The initial height values were determined from the compression stress–strain curves based on the probe position at which the force values started to increase. Average values and standard deviations were obtained from the analysis of ten replicates. Young's modulus and stress at compression of 40% were evaluated from the stress–strain curves using the approach described recently.53Circular dichroism
Circular dichroism (CD) measurements were carried out on a Jasco J-810 spectropolarimeter. The spectra were recorded in acrylic cell with 10 mm optical path for GBP-Fluo5 either in solution or entrapped in 1 mm thick hydrogel slab at 37 °C (in both cases, the concentration of GBP-Fluo5 was equal to 1 × 10−5 M). For this measurement polySBDMA-GBP-Fluo5 was prepared without BSA to prevent its spectra interfering with those of GBP-Fluo5.Static glucose sensing of free GBP-Fluo5 protein
GBP-Fluo5 protein was dissolved in AIF solution (concentration was equal to 1 × 10−5 M). Measurements were performed in the thermostated measurement cell (10 mm optical path) at 37 °C in a spectrofluorimeter (Shimadzu RF-5301PC, Japan). Experiments were carried out for glucose concentration range from 0 to 23 mM at the excitation wavelength for CFP of 433 nm. The ratio between the fluorescence intensities at 527 nm (YFP emission) and 475 nm (CFP emission) was evaluated as an indicator for change in FRET.Glucose sensing of entrapped GBP-Fluo5 protein in a perfusion system
PolySBDMA-GBP-Fluo5 hydrogel cylinders of 1 mm thickness were tested in a custom-made set-up in an acrylic cell using an excitation light of 405 nm from laser diode connected to one end of a cylinder and Ocean Optics QE 65000 (Ocean Optics, Dunedin, FL) light detector operated in the range from 200 to 1100 nm in 5 mm distance from a cylinder and at 90° angle to the excitation light beam. The measurements were performed under continuous perfusion with 0.5 mL min−1 flow of glucose solutions in AIF in the concentration range from 0 to 20 mM.Cycle-type glucose sensing of entrapped GBP-Fluo5 protein
The cycle-type of experiment was designed to determine the stability of GBP-Fluo5 protein entrapped in SBDMA hydrogel at 37 °C up to 7 days. The fluorescence spectra of polySBDMA-GBP-Fluo5 hydrogel cylinders were repeatedly determined for 5 and 10 mM glucose solutions in AIF. In this experiment, polySBDMA-GBP-Fluo5 hydrogel cylinder was stored in 5 mM glucose solutions in AIF at 37 °C in an incubator. After measuring the spectra, a cylinder was immersed to 10 mM glucose solution in AIF for 30 min followed by determining the fluorescence spectra. Then a cylinder was placed back to 5 mM glucose solution in AIF until the next cycle was performed.3. Results and discussion
Glucose diffusion coefficient in polySBDMA hydrogels
The diffusion coefficient of glucose in polySBDMA hydrogel was determined by the glucose release method described recently for characterization of glucose diffusion in the silica hydrogels.11 Fig. 1 shows the experimental dependence of glucose concentration in solution surrounding the hydrogel as a function of time. The experimental data were divided into two regions,54,55 i.e. those of “short times” and “long times”, which correspond to the short and long stages of diffusion, respectively. The short-time approximation is valid for the first 60% of the total released glucose, corresponding to the first 8 minutes of the release experiment. The experimental data can be fitted by the Ritger–Peppas model described by eqn (2):
 | (2) |
 | ||
| Fig. 1 The dependence of the fractional glucose release from polySBDMA hydrogel to solution on time. The dashed line for Mt/M∞ = 0.6 at t = 8 min separates the experimental data evaluated by short-time and long-time approximations, respectively. The inset shows the short-time experimental data fitted by eqn (2). | ||
The fitting of experimental data in a short-time region by eqn (2) is shown in the inset of Fig. 1. The obtained fitting parameters k and n were 0.1280 ± 0.0004 min−1 and 0.460 ± 0.003, respectively. The n-value close to 0.5 indicates that the glucose diffusion in polySBDMA can be characterized by the Fickian diffusion and, hence, this model can be used for estimation of the diffusion coefficients.10,55
Based on the Ritger–Peppas model,54,55 the short-time, DE, and long-time, DL, diffusion coefficients were determined from eqn (3) and (4), respectively:
 | (3) |
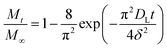 | (4) |
These equations are approximations of the equation that is obtained by solving the Fick's second law of diffusion under the following boundary conditions:56
| t = 0, −δ/2 < x < δ/2, c = c1 |
| t > 0, x = ±δ/2, c = c0 |
The experimental data in both the short and long stages of diffusion fitted by eqn (3) and (4) are shown in Fig. 2. The diffusion coefficients DE and DL were estimated to be 1.10 ± 0.05 × 10−10 m2 s−1 and 1.21 ± 0.03 × 10−10 m2 s−1, respectively. As can be seen, both fits gave similar values, thus it can be concluded that the diffusion coefficient of glucose in this polySBDMA hydrogel is approximately 1.2 × 10−10 m2 s−1. This value for the polySBDMA hydrogel with the solid content of 40% is comparable to values previously determined for glucose diffusion in biological materials such as bovine cornea (1.6 × 10−10 m2 s−1) and only slightly lower than those for human cornea (2.5–3 × 10−10 m2 s−1),57 hydrogels prepared by the sol–gel technique with the solid content of 11% (2.0 × 10−10 m2 s−1),11 poly(ethylene glycol)/poly(acrylic acid) hydrogels with the solid content of 30% (2.2 × 10−10 m2 s−1),58 and agar gel with the low solid content of 1.5% (2.2 × 10−10 m2 s−1).59
 | ||
| Fig. 2 Fitting of experimental data for glucose release from polySBDMA hydrogel with the short-time (a) and long-time (b) models using eqn (3) and (4). | ||
Estimation of equilibrium times for diffusion and release of glucose
The determination of glucose diffusion coefficient in polySBDMA hydrogels allows for discussions of some practical consequences for using this hydrogel in a glucose sensing device, where the glucose diffusion to entrapped GBP-Fluo5 is the limiting step for sensing the glucose level. Since this is related to hydrogel thickness and direction of glucose diffusion, these two factors are considered of general importance for all applications based on solute diffusion. Moreover, in the case of ionic types of hydrogels, the presence of electrolytes needs to be considered. In our case, the polymer chains of sulfobetaine-based hydrogel are in water in a collapsed conformation due to coulombic attraction between positively and negatively charged moieties.30 In the presence of an electrolyte that screens the interactions between these charged moieties, the polymer network is expanded30 and, consequently, the transport of glucose is expected to be enhanced compared to that in pure water. Therefore the diffusion coefficient determined in ultrapure water in this work is considered as the value, which may be increased in the physiological environment containing various ions.The hydrogel thickness has a strong influence on reaching the equilibrium between the glucose concentration in the hydrogel and the hydrogel surroundings. The equilibrium time is proportional to the square of the hydrogel thickness.56 In addition, the equilibrium time is related to the direction of the diffusion, i.e., the equilibrium times for egress and ingress can differ. In the case of glucose release (egress) from the hydrogel, the diffusion of glucose from a small finite volume into the infinity space has to be considered, whereas in the case of glucose diffusion into the hydrogel (ingress), glucose diffuses from the infinity space into the small volume of the hydrogel. Because of the glucose gradients and volume considerations, one intuitively feels that, at comparable experimental conditions, the time for complete glucose release from the hydrogel will be shorter than the time needed to reach an equilibrium situation for the glucose diffusion into the hydrogel. In the text below, the situations for both directions of glucose diffusion and reaching the equilibrium glucose concentration in the hydrogel and its surrounding solution are described in more detail.
The time needed to reach an equilibrium of glucose between the glucose concentration in the surrounding medium and the hydrogel matrix is important when the hydrogel serves as an immobilization matrix for the glucose sensing protein detecting the glucose diffusion from the external solution (e.g. blood or interstitial fluids). The equilibrium time can then be understood as a delay between the concentrations of glucose in the solution and in the hydrogel. Consequently, since the equilibrium time is proportional to the square of thickness of the hydrogel, the hydrogel should be as thin as possible to avoid significant delays between glucose concentrations in hydrogel and solution, as can be estimated from data shown in Fig. 3.
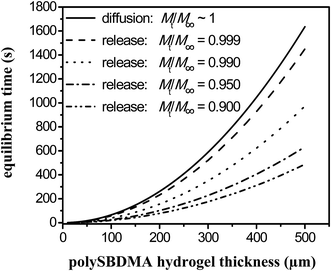 | ||
| Fig. 3 Estimation of the equilibrium time for diffusion into a hydrogel (ingress) and different values of fractional release of glucose from a hydrogel (egress) Mt/M∞ as a function of hydrogel thickness using eqn (9) and (10), respectively. | ||
To analyze the situation of glucose diffusion from the solution into the hydrogel correctly, one would need to describe the diffusion process into the small finite volume numerically. A simplified estimation of this situation can be proposed. The flow of glucose into the hydrogel and the total amount of glucose which penetrates across the hydrogel–solution interface into the hydrogel, can be approximately expressed by eqn (5):60
 | (5) |
After the integration of eqn (4) to (5), the total amount of glucose that penetrates across the interface into the hydrogel (in the infinity space approximation) can be estimated as follows:
 | (6) |
Eqn (6) can be rewritten to eqn (7), in which the amount, i.e., the concentration, of glucose in the hydrogel is expressed:
 | (7) |
Eqn (7) is determined by the surface area A, the thickness δ, and the glucose concentration in the solution kept constant at M0. Strictly speaking, this equation cannot precisely express a real situation due to the finite thickness of the real hydrogel. However, in the first approximation we may consider a simplification:
 | (8) |
The equilibrium time te, which corresponds to the time when the glucose concentration in the hydrogel is equal to the glucose concentration of surrounding solution, can then be expressed as:
 | (9) |
The dependence of equilibrium time on the thickness of polySBDMA hydrogel with D equal to 1.2 × 10−10 m2 s−1 calculated from eqn (9) is shown in Fig. 3 as the solid line.
Glucose release from the hydrogel to the solution is considered when glucose concentration in the hydrogel is higher than that in its surrounding. When glucose concentration in the surroundings is equal to zero, glucose diffuses from the hydrogel and this process can be analyzed using the Ritger–Peppas model for the release of solute from the hydrogel. For this analysis, eqn (4) describing the “long-time” diffusion is rewritten to eqn (10) providing the time when the initial glucose concentration is completely released (or released to the given value of fractional release at the long stage of the glucose release experiment):
 | (10) |
Fig. 3 shows the times estimated to achieve the selected fractional releases of glucose, between 90.0 and 99.9% of initial glucose concentration, from the hydrogel of specific thickness using the diffusion coefficient of 1.2 × 10−10 m2 s−1. From mathematical reason (ln(0)), it is not possible to consider that the release would equal 100%. Hence, a release equal to 99.9% is considered as the “complete release”. These results thus show differences between the diffusion into the hydrogel and the release from the hydrogel into the solution as long as the values equal to tr < te. Even in the case of 99.9% release of glucose, the equilibrium time of this release is lower than the equilibrium time for complete diffusion into the hydrogel.
Molecular weight cut-off and pore-size distribution for the polySBDMA hydrogel
Inverse size-exclusion chromatography was applied to obtain the information on MWCO and the PSD of the polySBDMA hydrogel. The representative elution curves of pullulan standards and saccharose are shown in Fig. 4. Standards with a wide range of molecular weights were used including both those which are completely excluded from the hydrogel pores (i.e. high molecular weight pullulans) and those which completely penetrate into the pores (i.e. low molecular weight pullulans and saccharose). Fig. 4 reveals that the pullulan standards with molecular weights above 11.8 kDa (in the range from 22 to 113 kDa) are excluded from the pores of the hydrogel, because their elution curves are independent of their molecular weight. The subsequent evaluation of chromatographic partition coefficient for each ith pullulan standard and data fitting by the Boltzmann function results in the calibration curve are shown in Fig. 5a. The exclusion limit determining the MWCO value is about 8.5 kDa. This value obtained by pullulan standards can be converted to the viscosity radius Rη equal to 2.1 nm,51 which can be further converted to the MWCO value of 19 kDa towards globular proteins.51 The first derivative of the Boltzmann fit of the calibration curve is shown in Fig. 5b and provides the information on the PSD expressed as the HWHM value. The molecular weight range between 1.2 and 2.5 kDa obtained from the pullulan standards corresponds to the hydrodynamic radius difference of 0.44 nm. This relatively narrow PSD is consistent with the previously determined crosslink distance of this hydrogel of 3.0 ± 0.5 nm.33 These characteristics lead to two immediate consequences. First, this type of polySBDMA hydrogel is capable of permanently entrapping GBP-Fluo5, which has a molecular weight of 91.4 kDa and a hydrodynamic radius Rη of 3.9 nm.49 Second, in case such hydrogel with the entrapped protein is used under in vivo conditions (e.g. in an implant), the effective attack of the GBP-Fluo5 by the host's immune system should be prevented. The hydrogel can thus serve as an immunoprotective barrier preventing most of the complement proteins from permeating into the hydrogel matrix.61 This feature in combination with the biocompatibility and non-biofouling properties of a polySBDMA hydrogel makes this material highly attractive as the immobilization matrix for sensing proteins used for in vivo applications.Stability and glucose sensitivity of GBP-Fluo5 entrapped in the polySBDMA hydrogel
The data obtained from permeability analysis of polySBDMA hydrogel shows that this hydrogel should be suitable for permanent entrapment of GBP-Fluo5. The leaching of GBP-Fluo5 tested in PBS solution for 6 weeks at 37 °C was insignificant and less than 2% as determined by Bradford and fluorescence measurements.The conformational stability of GBP-Fluo5 after its entrapment into the hydrogel was studied by means of circular dichroism (CD). The CD spectrum of proteins at the near-UV end of the spectrum provides information about secondary structures of a polypeptide chain such as α-helix, β-sheet, and coil,62 and, therefore, it can be used to monitor changes in conformation of protein under different conditions. Fig. 6 shows indistinguishable CD spectra, in the range from 200 to 350 nm, of GBP-Fluo5 in PBS solution and in the polySBDMA-GBP-Fluo5 hydrogel after preparation and after storage for one week in PBS solution at 37 °C. This data reveals that the GBP-Fluo5 retains its original secondary structure after entrapment in the hydrogel.
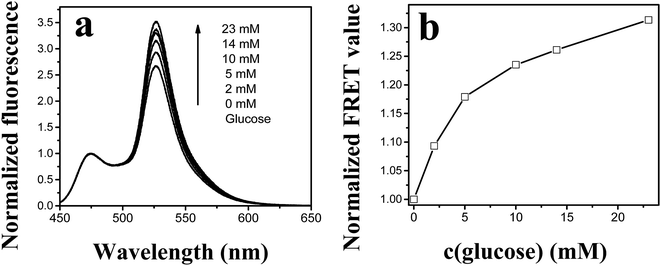
Fig. 7 demonstrates the glucose sensitivity of the GBP-Fluo5 in AIF solution investigated by a fluorescence spectroscopy in the physiological glucose concentration range between 0 and 23 mM. FRET, as a non-radiative coupling, was observed between the donor CFP part of GBP-Fluo5 construct emitting fluorescence at 475 nm and the acceptor YFP part of GBP-Fluo5 construct with an absorption maximum at 470 nm and emitting fluorescence at 527 nm. The FRET is expressed as a ratio between the intensity of fluorescence emissions at 527 nm and 475 nm. The increase in fluorescence emission with increased glucose concentration is well-visible by normalizing the fluorescence spectra to the fluorescence intensity at the maximum of CFP emission at 475 nm as (Fig. 7a). The resulting FRET values, normalized to the FRET at zero glucose concentration as shown in Fig. 7b, increase by about 30% for glucose concentrations between zero and 23 mM, which represents a sufficient GBP-Fluo5 sensitivity to precisely monitor the glucose levels in the physiological range.
Subsequently, the glucose sensitivity of GBP-Fluo5 entrapped in the polySBDMA-GBP-Fluo5 hydrogel was followed by the real-time changes in the FRET values in a perfusion system. In hydrogel formation, BSA was used as a stabilizing agent for protein.63 BSA does not interfere with measuring the glucose levels by fluorescence and FRET analysis. The data obtained in the perfusion system, carried out using a custom-made set-up consisting of a 405 nm excitation laser diode and an Ocean Optics light detector, are shown in Fig. 8. First, the glucose concentration was increased from 0 to 20 mM, successively via glucose concentrations of 2, 5, 10 and 15 mM, that was associated with increased FRET values from 2.94 to 3.5. Subsequently, the concentration of glucose was decreased from 20 mM to 2 mM resulting in decreased FRET values to about 3.2 (Fig. 8a). The equilibrium in glucose concentration was achieved during the first 20–25 minutes after changing the glucose solutions of different glucose concentrations. These values are consistent with the time estimated to reach the equilibrium derived from the glucose diffusion experiments (Fig. 3) considering the release of glucose from a hydrogel matrix with a thickness of 0.5 mm that is the maximum diffusion distance for a cylindrical geometry with diameter of 1 mm used in this experiment. Hence, the diffusion coefficients for glucose determined in pure water may be considered as the diffusion characteristic for this hydrogel also in a more complex fluids containing small electrolytes, such as AIF, which likely do not significantly contribute to hydrophilicity of hydrogel responsible for the glucose transport. Due to very low concentration of GBP-Fluo5 (∼10−5 M), the effect of its presence in hydrogel on glucose uptake is also not expected.
Plotting FRET values as a function of glucose concentration (Fig. 8b) leads to estimation of KD value for GBP-Fluo5 entrapped in polySBDMA hydrogel equal to 8.2 mM. This value is in the proper range with respect to the potential application for clinical in vivo glucose detection since the sensor must operate minimally in the range of glucose concentration between 0.5 and 20 mM.64 The high sensitivity of GBP-Fluo5 protein in the hypoglycemic range is noteworthy. There is approximately a 10% decrease in FRET values for a decrease in glucose concentration from 5 to 1 mM that is a considerable change to the overall signal change in the hypo and hyperglycemic ranges. Therefore, this protein may be deemed as the hypoglycemia indicator. The comparison of data for GBP-Fluo5 in solution (Fig. 7b) and entrapped in a hydrogel (Fig. 8b) shows that although the sensing GBP-Fluo5 molecule is the same in both static and perfusion experiments, the relative increase in FRET signal upon increasing the glucose concentration is slightly different, i.e., about 30% in the former case and about 20% in the latter case. This is due to used excitation wavelengths as well as the sensitivities at particular wavelength of individual detectors of these two different set-ups used for FRET detection.
Fig. 8c shows the cycle-type of experiment, which is based on determination of FRET changes during repeatedly changing the glucose concentrations between 5 and 10 mM performed over 7 days at 37 °C. The FRET values of around 3.0 and around 3.3 periodically change in correlation with the actual glucose levels of 5 and 10 mM, respectively. These data confirm repeatability in glucose sensing and stability of entrapped GBP-Fluo5 as well as applicability of this hydrogel–protein combination under body temperature. The photograph of cylindrical waveguide is shown in Fig. 8d.
Finally, the mechanical properties of both polySBDMA and polySBDMA-GBP-Fluo5 hydrogels were investigated. The stress at the compression to 40% deformation were determined to be 91 ± 17 and 92 ± 20 kPa and Young's moduli were 57 ± 12 and 55 ± 15 kPa for these hydrogels, respectively. These results demonstrate that the presence of GBP-Fluo5 and the immobilization process do not influence the mechanical stability of the polySBDMA hydrogel. These values are in the same range as those determined in our previous investigations on SBDMA-based hydrogels.33
4. Conclusion
A polySBDMA hydrogel was prepared and characterized in terms of glucose diffusion and porosity. Label-free glucose diffusion measurement determined by the egress of the glucose from the hydrogel was established and the diffusion coefficient was estimated to be approximately 1.2 × 10−10 m2 s−1. A careful evaluation of the data using the Ritger–Peppas model confirmed faster release of the glucose from the hydrogel than its diffusion into the hydrogel. A delay between the concentration of the glucose in the solution was shown to be significantly affected by the thickness of the hydrogel. The application of the inverse size-exclusion chromatography allowed to define the quantities of molecular weight cut-off and pore-size distribution of the hydrogel to be of 8 kDa (to pullulan) and 0.44 nm, respectively. The GBP-Fluo5 glucose biosensor protein was synthesized and permanently entrapped in the polySBDMA hydrogel. It retained its ability to undergo glucose-dependent changes at a physiological range of glucose, which were monitored as changes in the FRET emission. These results, together with highly biocompatible and non-biodegradable character of polySBDMA, constitute a promising approach for the preparation of fluorescent biosensors for real-time in situ glucose monitoring.Acknowledgements
The research was supported by the Sixth Framework Program of the EU, IP-031867, P. Cezanne and by the Slovak Research and Development Agency under the contract No. APVV-0486-10 and APVV-14-0858. J. M. and IL thank also to projects VEGA-2/0142/14 and VEGA-2/0198/14, respectively. D. Behulova, MD, from Children Faculty Hospital (DFNsP) in Bratislava is acknowledged for the possibility to measure the glucose concentrations using the clinical glucometer. We are grateful to Mrs E. Hipka from the Polymer Institute SAS for the technical assistance with the glucose egress measurements. This contribution is the result of the project implementation: Centre for materials, layers and systems for applications and chemical processes under extreme conditions supported by the Research & Development Operational Programme funded by the ERDF.Notes and references
- R. K. Shervedani, A. H. Mehrjardi and N. Zamiri, Bioelectrochemistry, 2006, 69, 201–208 CrossRef CAS PubMed.
- C. Wu, H. Sun, Y. Li, X. Liu, X. Du, X. Wang and P. Xu, Biosens. Bioelectron., 2015, 66, 350–355 CrossRef CAS PubMed.
- S. Moldoveanu, W. Scott and J. Zhu, J. Sep. Sci., 2015, 38, 3677–3686 CrossRef CAS PubMed.
- R. Rawer, W. Stork and C. F. Kreiner, Graefe's Arch. Clin. Exp. Ophthalmol., 2004, 242, 1017–1023 CrossRef CAS PubMed.
- H. Guo, W. Jiang, X. Pang, F. Wu and F. Liu, Anal. Methods, 2012, 4, 265–269 RSC.
- L. C. Clark and C. Lyons, Ann. N. Y. Acad. Sci., 1962, 102, 29–45 CrossRef CAS PubMed.
- J. Wang, Chem. Rev., 2008, 108, 814–825 CrossRef CAS PubMed.
- P. Benvenuto, A. K. M. Kafi and A. Chen, J. Electroanal. Chem., 2009, 627, 76–81 CrossRef CAS.
- M. V. Kuzimenkova, A. E. Ivanov, C. Thammakhet, L. I. Mikhalovska, I. Y. Galaev, P. Thavarungkul, P. Kanatharana and B. Mattiasson, Polymer, 2008, 49, 1444–1454 CrossRef CAS.
- L. Serra, J. Domenech and N. A. Peppas, Biomaterials, 2006, 27, 5440–5451 CrossRef CAS PubMed.
- I. Krupa, T. Nedelčev, D. Chorvát Jr, D. Račko and I. Lacík, Eur. Polym. J., 2011, 47, 1477–1484 CrossRef CAS.
- A. S. Hoffman, Adv. Drug Delivery Rev., 2012, 64, 18–23 CrossRef.
- P. M. Kharkar, K. L. Kiick and A. M. Kloxin, Chem. Soc. Rev., 2013, 42, 7335–7372 RSC.
- M. R. Aguilar and J. San Román, Smart Polymers and their Applications, Woodhead Publishing Limited, 2014 Search PubMed.
- N. A. Peppas, J. Z. Hilt, A. Khademhosseini and R. Langer, Adv. Mater., 2006, 18, 1345–1360 CrossRef CAS.
- B. Yu, C. Wang, Y. M. Ju, L. West, J. Harmon, Y. Moussy and F. Moussy, Biosens. Bioelectron., 2008, 23, 1278–1284 CrossRef CAS PubMed.
- R. Baronas, F. Ivanauskas, I. Kaunietis and V. Laurinavicius, Sensors, 2006, 6, 727–745 CrossRef.
- F. Jia, B. Narasimhan and S. Mallapragada, Biotechnol. Bioeng., 2014, 111, 209–222 CrossRef CAS PubMed.
- R. Gupta and N. K. Chaudhury, Biosens. Bioelectron., 2007, 22, 2387–2399 CrossRef CAS PubMed.
- R. C. Rodrigues, C. Ortiz, A. Berenguer-Murcia, R. Torres and R. Fernández-Lafuente, Chem. Soc. Rev., 2013, 42, 6290–6307 RSC.
- R. A. Sheldon, Adv. Synth. Catal., 2007, 349, 1289–1307 CrossRef CAS.
- J. R. Retama, B. Lopez-Ruiz and E. Lopez-Cabarcos, Biomaterials, 2003, 24, 2965–2973 CrossRef CAS PubMed.
- M. Hamidi, A. Azadi and P. Rafiei, Adv. Drug Delivery Rev., 2008, 60, 1638–1649 CrossRef CAS PubMed.
- T. Vermonden, R. Censi and W. E. Hennink, Chem. Rev., 2012, 112, 2853–2888 CrossRef CAS PubMed.
- J. B. Schenoff, Langmuir, 2014, 30, 9625–9636 CrossRef PubMed.
- D. Dong, J. Li, M. Cui, J. Wang, Y. Zhou, L. Luo, Y. Wei, L. Ye, H. Sun and F. Yao, ACS Appl. Mater. Interfaces, 2016, 8, 4442–4455 CAS.
- S. Chen and S. Jiang, Adv. Mater., 2008, 20, 335–338 CrossRef CAS.
- Z. Zhang, M. Zhang, S. Chen, T. A. Horbett, B. D. Ratner and S. Jiang, Biomaterials, 2008, 29, 4719–4725 CrossRef CAS PubMed.
- Z. Zhang, T. Chao, L. Liu, G. Cheng, B. D. Ratner and S. Jiang, J. Biomater. Sci., Polym. Ed., 2009, 20, 1845–1859 CrossRef CAS PubMed.
- A. B. Lowe and C. L. McCormick, Polyelectrolytes and polyzwitterions: Synthesis, properties, and applications, ACS Books, Washington DC, 2006 Search PubMed.
- P. Sobolčiak, P. Kasák and I. Lacík, Chem. Pap., 2011, 105, 918–925 Search PubMed.
- Z. Zhang, T. Chao and S. Jiang, J. Phys. Chem. B, 2008, 112, 5327–5332 CrossRef CAS PubMed.
- P. Kasák, I. Krupa, Z. Kroneková and I. Lacík, Polymer, 2011, 52, 3011–3020 CrossRef.
- M.-S. Steiner, A. Duerkop and O. S. Wolfbeis, Chem. Soc. Rev., 2011, 40, 4805–4839 RSC.
- F. Khan, L. Gnudi and J. C. Pickup, Biochem. Biophys. Res. Commun., 2008, 365, 102–106 CrossRef CAS PubMed.
- J. Galbán, I. Sanz-Vicente, E. Ortega, M. Del Barrio and S. De Marcos, Anal. Bioanal. Chem., 2012, 402, 3039–3054 CrossRef PubMed.
- B. S. Der and J. D. Dattelbaum, Anal. Biochem., 2008, 375, 132–140 CrossRef CAS PubMed.
- H. V. Hsieh, D. B. Sherman, S. A. Andaluz, T. J. Amiss and J. B. Pitner, J. Diabetes Sci. Technol., 2012, 6, 1286–1295 CrossRef PubMed.
- J. Siegrist, T. Kazarian, C. Ensor, S. Joel, M. Madou, P. Wang and S. Daunert, Sens. Actuators, B, 2010, 149, 51–58 CrossRef CAS.
- R. W. Jacobson, K. Weidemaier, J. Alarcon, C. Herdman and S. Keith, US Pat. 2005/0113658 A1, Becton Dickinson and Co., 2005.
- S. Joel, K. B. Turner and S. Daunert, ACS Chem. Biol., 2014, 9, 1595–1602 CrossRef CAS PubMed.
- T. Saxl, F. Khan, M. Ferla, D. Birch and J. Pickup, Analyst, 2011, 136, 968 RSC.
- H. V. Hsieh, J. B. Pitner, T. J. Amiss, C. M. Nyez, D. B. Sherman and D. J. Wright, US Pat. 2007/0281368 A1, 2007.
- L. Schenkman, M. Koukaki, S. Karamanou, and A. Economou, IEEE Eng. Med. Biol. Soc., 2007, vol. 1, pp. 6060–6063 Search PubMed.
- C. Strohhöfer, T. Förster, D. Chorvát Jr, P. Kasák, I. Lacík, M. Koukaki, S. Karamanou and A. Economou, Phys. Chem. Chem. Phys., 2011, 13, 17852–17863 RSC.
- T. Förster, C. Strohhöfer, K. Bock, P. Kasák, M. Danko, Z. Kroneková, T. Nedelčev, I. Krupa and I. Lacík, Transducers, 2009, 2009, 1218–1221 Search PubMed.
- Q. Shao and S. Jiang, Adv. Mater., 2015, 27, 15–26 CrossRef CAS PubMed.
- N. Fogh-Andersen, B. M. Altura, B. T. Altura and O. Siggaard-Andersen, Clin. Chem., 1995, 41, 1522–1525 CAS.
- E. A. Kapellios, S. Karamanou, M. F. Sardis, M. Aivaliotis, A. Economou and S. A. Pergantis, Anal. Bioanal. Chem., 2011, 399, 2421–2433 CrossRef CAS PubMed.
- K. Deuschle, S. Okumoto, M. Fehr, L. L. Looger, L. Kozhukh and W. B. Frommer, Protein Sci., 2005, 14, 2304–2314 CrossRef CAS PubMed.
- M. Brissova, M. Petro, I. Lacík, A. C. Powers and T. Wang, Anal. Biochem., 1996, 242, 104–111 CrossRef CAS PubMed.
- M. Brissova, I. Lacík, A. C. Powers, A. V. Anilkumar and T. Wang, J. Biomed. Mater. Res., 1998, 39, 61–70 CrossRef CAS PubMed.
- I. Krupa, T. Nedelčev, D. Račko and I. Lacík, J. Sol-Gel Sci. Technol., 2010, 53, 107–114 CrossRef CAS.
- P. L. Ritger and N. A. Peppas, J. Controlled Release, 1987, 5, 37–42 CrossRef CAS.
- P. L. Ritger and N. A. Peppas, J. Controlled Release, 1987, 5, 23–36 CrossRef CAS.
- J. Crank, The Mathematics of Diffusion, Claredon Press, Oxford, 2nd edn, 1975 Search PubMed.
- D. Myung, K. Derr, P. Huie, J. Noolandi, K. P. Ta and C. N. Ta, Ophthalmic Res., 2006, 38, 158–163 CrossRef CAS PubMed.
- D. Myung, N. Farooqui, D. Waters, S. Schaber, W. Koh, M. Carrasco, J. Noolandi, C. W. Frank and C. N. Ta, Curr. Eye Res., 2008, 33, 29–43 CrossRef CAS PubMed.
- L. Weng, S. Liang, L. Zhang, X. Zhang and J. Xu, Macromolecules, 2005, 38, 5236–5242 CrossRef CAS.
- J. J. Pérez-Bueno, R. Ramírez-Bon, Y. V. Vorobiev, F. Espinoza-Beltrán and J. González-Hernández, Thin Solid Films, 2000, 379, 57–63 CrossRef.
- A. M. A. Rokstad, I. Lacik, P. de Vos and B. L. Strand, Adv. Drug Delivery Rev., 2014, 67–68, 111–130 CrossRef CAS PubMed.
- N. J. Greenfield, Nat. Protoc., 2007, 1, 2876–2890 CrossRef PubMed.
- B. S. Chang and R. R. Mahoney, Biotechnol. Appl. Biochem., 1995, 22, 203–214 CAS.
- J. C. Pickup, F. Hussain, N. D. Evans and N. Sachedina, Biosens. Bioelectron., 2005, 20, 1897–1902 CrossRef CAS PubMed.
Footnote |
| † Previous address: Polymer Institute of the Slovak Academy of Sciences, Dúbravská cesta 9, 845 41 Bratislava, Slovakia. |
| This journal is © The Royal Society of Chemistry 2016 |