Mechanical and structural properties of graphene-like carbon nitride sheets

Abstract

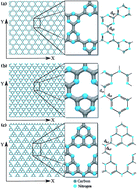
Carbon nitride-based nanostructures have attracted special attention (from theory and experiments) due to their remarkable electromechanical properties. In this work we have investigated the mechanical properties of some graphene-like carbon nitride membranes through fully atomistic reactive molecular dynamics simulations. We have analyzed three different structures of these CN families, the so-called graphene-based g-CN, triazine-based g-C₃N₄ and heptazine-based g-C₃N₄. The stretching dynamics of these membranes was studied for deformations along their two main axes and at three different temperatures: 10 K, 300 K and 600 K. We show that g-CN membranes have the lowest ultimate fracture strain value, followed by heptazine-based and triazine-based ones, respectively. This behavior can be explained in terms of their differences in density values, topologies and types of chemical bonds. The dependency of the fracture patterns on the stretching directions is also discussed.

---

Introduction

Since the predictions made by Liu and Cohen,^1–3 carbon nitrides (CN) have been of particular interest in the search for new functional materials. Their theoretical calculations have pointed out that CN crystals should present extremely high bulk modulus, of the order of 427 GPa.^1–3 Cubic-C₃N₄ is predicted to exhibit higher bulk modulus than that of diamond,⁴ while β-C₃N₄ can exhibit a tunable electronic character, going from metallic to insulating depending on the morphology.⁵ These promising results motivated many different experimental investigations on distinct CN forms. Successful synthesis of materials like small β-C₃N₄ crystals, amorphous CN films^6,7 and nanofibers made from C₃N₄ and CN have been reported.⁸

The recent isolation of graphene membranes,⁹ with its unique electrical and mechanical properties^10–12 and various applications in nanotechnology,^13–16 has renewed the interest in two dimensional materials. Other two dimensional structures, such as boron nitride¹⁷ and silicene,¹⁸ among others, have been object of recent investigations. However, bidimensional CN structures have not been thoroughly investigated yet, in spite of their very promising mechanical and electronic properties.^19–22

The successful synthesis of the carbon nitride graphitic phase is still a topic of debate. However, some evidence of its synthesis has been reported,^23–29 while the synthesis of its polymeric phase, melon, is well documented.^30,31 These materials are porous, low-density, hard, chemically inert, biocompatible structures,³² with unusual optical and electronic properties.^27,28,33,34 These properties can be, in principle, exploited in a large class of technological applications.

Understanding the mechanical properties of novel materials is essential in order to enable the design of applications. In this work we have investigated the mechanical and fracture patterns of three members of the two dimensional CN family (Fig. 1): graphene-based g-CN, triazine-based g-C₃N₄ and heptazine-based g-C₃N₄. We have carried out fully atomistic reactive molecular dynamics simulations considering different stretching directions (along their main axes) and at different temperatures. We expect this work to provide an extensive analysis on the behavior of graphitic CN structures under mechanical stress, as well as motivate further investigations.

Fig. 1 Structural schemes of the investigated sheets: (a) graphene-based g-CN; (b) triazine-based g-C₃N₄, and; (c) heptazine-based g-C₃N₄ membranes. The insets show their corresponding unit cell and highlights some important bond-lengths.

Methodology

All calculations were carried out with reactive classical molecular dynamics methods using the ReaxFF force field,³⁵ as implemented in the LAMMPS package.³⁶ ReaxFF was developed in order to simulate large systems while keeping an accurate description of bond formation and bond break processes. This method employs total energy description based on partial energy contributions, such as bond elongation, van der Waals forces and Coulomb interactions, among others. The ReaxFF ability to dynamically describe hybridization changes and charge redistribution (allowing the description of creating/breaking bonds), makes it suitable for the present study.

ReaxFF parameters are obtained from experiments and/or DFT calculations. The mean deviation between the heat of formation predicted by this method and experimental data is no larger than 2.9 kcal mol⁻¹ for hydrocarbon systems.³⁷ To further assess the suitability of the employed parameter set,³⁵ we compared the predicted structures of β-C₃N₄ and graphitic-C₃N₄ with other values previously reported in the literature.⁴ The differences on bond-length and lattice parameter values were of 1% and 2% respectively, thus corroborating the adequacy of the used parameter set for this family of structures.

The investigated models consist of three different carbon nitride membranes called here: graphene-based g-CN, triazine-based g-C₃N₄ and heptazine-based g-C₃N₄, as shown in Fig. 1. The considered membranes in this work have dimensions around of 160 × 150 Å, where the g-CN structure has 6068 atoms, triazine-based g-C₃N₄ and heptazine-based g-C₃N₄ ones, 9240 and 8624 atoms, respectively. All structures were considered with periodic boundary conditions along the X and Y directions. To assure that each structure was at equilibrium before the start of the stretching process, we first thermalized them. In order to do this, we ran the molecular dynamics simulations under the NPT ensemble, i.e., with fixed number of atoms, pressure and temperature values. External pressure was set to zero, so we had no initial stress on any structure. The value of the chosen temperature was controlled during the stretching process through a Nosé–Hoover chain thermostat.³⁸ Three different temperatures values were considered (10 K, 300 K and 600 K), in order to determine how dependent the mechanical properties are on thermal effects.

The stretching process was simulated through the gradual increase of the lattice parameter along the periodic directions. A timestep of 0.05 fs was used together with a constant strain rate of 10⁻⁶ per fs. The increased stretching is maintained until complete rupture of the membranes, which means typical simulation times of the order of 10⁶ fs. The methodology used in this work has been successfully applied in the study of the mechanical properties of many other structures.^39–44

From the simulated stretching processes we can obtain the stress–strain curves. In the linear region of the stress–strain curve we have calculated the Young's modulus, which can be defined as

where ε_i is the strain along direction i and σ_ii is the in-plane virial stress tensor component along direction i, defined aswhere V is the volume of the membrane, N is the number of atoms, v the velocity, r the position and f the force per atom. As the membrane is only one atom-thick and atomic volumes are not very well-defined, we opt to calculate all Young's moduli as a function of this thickness d, effectively writing the volume V as V = Ad, where A is the surface area of the membrane.

In order to have a better estimation of the spatial stress distribution during the stretching regime, we have also calculated the von Mises stress per atom i, defined as

Results and discussions

The three distinct membranes, graphene-based g-CN, triazine-based g-C₃N₄ and heptazine-based g-C₃N₄ (Fig. 1) were stretched at a constant rate until complete rupture. Table 1 summarizes the critical strain values (i.e., strain values at the point where fracture starts) for the three structures at three different temperatures, and for two distinct strain directions. We can see a clear difference for these values for each structure. This can be explained by the considerable difference in the strain energies associated with each stretched membrane. In the case of graphene-based g-CN, there are C–C single bonds, which are naturally weaker than resonant C–N bonds. The presence of these bonds decreases the strain energy associated with the stretched membrane, therefore making it easier to fracture. In the cases of heptazine-based and triazine-based g-C₃N₄, both present the same types of bonds, i.e., single and double C–N bonds, but the pore density and, therefore, the number of these chemical bonds in their unit cells, is considerably different for each case. Heptazine-based structures show a lower density of chemical bonds than triazine-based structures, meaning a lower strain energy associated with the former. From these arguments, we can understand the variation on the critical strain values due to their different topologies. The decrease of the strain rate values with the increase of temperature is an expected effect, as higher thermal energy increases the fluctuations, thus making bond breaking easier.

Table 1 Critical strain values

Direction	Temperature (K)	g-CN	Heptazine g-C3N4	Triazine g-C3N4
X	10	0.132	0.149	0.183
Y	10	0.172	0.178	0.204
X	300	0.114	0.129	0.150
Y	300	0.150	0.140	0.170
X	600	0.100	0.104	0.130
Y	600	0.120	0.120	0.137

---

The distinct morphologies of each membrane type lead to different fracture patterns. Also, these patterns depend on the direction of the applied strain. We applied strain along the two principal directions, X and Y, as defined in Fig. 2–4. Fig. 2 shows that, when stretching a graphene-based g-CN sheet along the X direction, stress accumulates on the C–C single bonds that are almost parallel to that direction. These are the first bonds to break. When the strain is applied along the Y direction, the C–C single bonds are parallel to the stretching direction, thus much less stress is built up before the fracturing process starts, ultimately breaking these single bonds.

Fig. 2 MD snapshots showing the stretch process considering (a and b) X and (c and d) Y directions for the g-CN membrane. The insets show the beginning of the fracture process. The von Mises stress values indicate the stress distribution during the process by color scale labeled in the figure.

Fig. 3 MD snapshots showing the stretch process considering (a and b) X and (c and d) Y directions for the triazine g-C₃N₄ membrane. The insets show the beginning of the fracture process. The von Mises stress values indicate the stress distribution during the process by color scale labeled in the figure.

Fig. 4 MD snapshots showing the stretch process considering (a and b) X and (c and d) Y directions for the heptazine g-C₃N₄ membrane. The insets show the beginning of the fracture process. The von Mises stress values indicate the stress distribution during the process by color scale labeled in the figure.

For triazine-based g-C₃N₄ membranes, as shown in Fig. 3, the stress also builts up mostly into the single bonds, in this case C–N. When stretching along the X direction, fracture yields rough edges, while stretching along the Y direction fracture yields very clean edges. This is due to the single C–N bonds which are aligned with that direction, breaking in succession.

A very similar behavior is observed in the case of heptazine-based g-C₃N₄ membranes, as shown in Fig. 4. This should be expected as, despite presenting larger macro-cycles, the heptazine-based membranes present a very similar structure to that of triazine-based membranes. The types of chemical bonds are almost the same, as well as, their alignment with the stretching directions, X and Y. Therefore, while the critical strain values vary significantly between each of these structures, due to the different density (number) of chemical bonds, the stress and fracture patterns are very similar.

Stress–strain curves for all the considered structures and temperatures are presented in Fig. 5. In general, the stress–strain curves start with a linear region where the Young's modulus can be calculated, going through a non-linear region and until the total rupture. Analyzing the stress–strain curves, we observe that for the graphene-based g-CN membranes a direct transition from linear regime to the fracture occurs. For the triazine g-C₃N₄ and heptazine g-C₃N₄, after the linear region, the stress is momentarily relieved and another linear region can be observed, leading to a complete fracture afterwards. This stress decrease can be attributed to an internal rearrangement of bond lengths and angles. Similar behavior in membranes formed by carbon, nitrogen and boron was observed using the Tersoff potential.⁴⁵

Fig. 5 Stress–strain curves of the carbon nitride sheets (g-CN, heptazine g-C₃N₄ and triazine g-C₃N₄) for different directions and temperatures.

The Young's modulus for all considered structures, directions and temperatures were obtained by fitting the linear region of the stress–strain curves. For instance, considering the room temperature (300 K) and the X direction, the obtained value for g-CN was 1663 GPa Å, while for triazine g-C₃N₄ 1668 GPa Å and heptazine g-C₃N₄ 1247 GPa Å, as can be seen along with another results in Table 2. Our results are in good agreement with previously theoretical values obtained from a recent work with Tersoff potential for the case of triazine-based g-C₃N₄.⁴⁵

Table 2 Young's modulus values

Structure	Temperature (K)	Young's modulus (GPa Å)	Direction
g-CN	10 K	1675	X
Heptazine	10 K	1356	X
Triazine	10 K	1890	X
g-CN	10 K	1516	Y
Heptazine	10 K	1397	Y
Triazine	10 K	1920	Y
g-CN	300 K	1663	X
Heptazine	300 K	1247	X
Triazine	300 K	1668	X
g-CN	300 K	1349	Y
Heptazine	300 K	1299	Y
Triazine	300 K	1733	Y
g-CN	600 K	1571	X
Heptazine	600 K	1197	X
Triazine	600 K	1578	X
g-CN	600 K	1333	Y
Heptazine	600 K	1229	Y
Triazine	600 K	1575	Y

---

Comparing the calculated value of the Young's modulus for graphene (3570 GPa Å (ref. 46)) with the values herein reported, CN membranes values are lower by 53% for g-CN and triazine g-C₃N₄ and 65% for heptazine g-C₃N₄. This decrease is due to differences in the chemical structure of the carbon nitride sheets when compared to graphene, namely the presence of pores, decreasing the density of chemical bonds, as well as the presence of single bonds.

Summary and conclusions

We have investigated the mechanical and fracture patterns of a series of two-dimensional CN structures: g-CN, triazine g-C₃N₄ and heptazine g-C₃N₄ (Fig. 1). The study was carried out through fully atomistic reactive molecular dynamics simulations using the ReaxFF force field. The Young's moduli for the carbon nitride membranes are smaller when compared with the Young's modulus for graphene. This can be understood by presence of pores and single C–N bonds in the carbon nitride membranes. More interestingly, graphene-based g-CN goes abruptly from elastic to brittle behavior, while triazine and heptazine g-C₃N₄ structures go through significant structural reconstructions with multiple elastic stages. This differentiated behavior can be explained by the differences in the density of chemical bonds and how the rings are oriented in relation to the stretching directions, resembling an arch-type effect recently reported to silicene membranes.⁴²

Acknowledgements

This work was supported in part by the Brazilian Agencies CAPES, CNPq and FAPESP. The authors thank the Center for Computational Engineering and Sciences at Unicamp for financial support through the FAPESP/CEPID Grant # 2013/08293-7. J. M. S. acknowledges the support from CAPES through the Science Without Borders program (project number A085/2013).

References

1. M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 32, 7988.
2. A. Y. Liu and M. L. Cohen, Science, 1989, 245, 841–842.
3. A. Y. Liu and R. M. Wentzcovitch, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 10362.
4. D. M. Teter and R. J. Hemley, Science, 1996, 271, 53–55.
5. Y. Miyamoto, M. L. Cohen and S. G. Louie, Solid State Commun., 1997, 102, 605–608.
6. C. Niu, Y. Z. Lu and C. M. Lieber, Science, 1993, 261, 334–337.
7. K. M. Yu, M. L. Cohen, E. Haller, W. Hansen, A. Y. Liu and I. Wu, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 5034.
8. M. Terrones, P. Redlich, N. Grobert, S. Trasobares, W.-K. Hsu, H. Terrones, Y.-Q. Zhu, J. P. Hare, C. L. Reeves, A. K. Cheetham, H. W. K. Manfred Ruhle and D. R. M. Walton, Adv. Mater., 1999, 11, 655–658.
9. K. S. Novoselov, A. K. Geim, S. Morozov, D. Jiang, Y. Zhang, S. Dubonos, I. Grigorieva and A. Firsov, Science, 2004, 306, 666–669.
10. C. Berger, Z. Song, X. Li, X. Wu, N. Brown, C. Naud, D. Mayou, T. Li, J. Hass and A. N. Marchenkov, Science, 2006, 312, 1191–1196.
11. A. K. Geim, Science, 2009, 324, 1530–1534.
12. C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388.
13. R. Joshi, P. Carbone, F. Wang, V. Kravets, Y. Su, I. Grigorieva, H. Wu, A. Geim and R. Nair, Science, 2014, 343, 752–754.
14. X. Yang, C. Cheng, Y. Wang, L. Qiu and D. Li, Science, 2013, 341, 534–537.
15. L. Feng, L. Wu and X. Qu, Adv. Mater., 2013, 25, 168–186.
16. Y. Tao, Y. Lin, Z. Huang, J. Ren and X. Qu, Adv. Mater., 2013, 25, 2594–2599.
17. W. Auwärter, T. Kreutz, T. Greber and J. Osterwalder, Surf. Sci., 1999, 429, 229–236.
18. P. Vogt, P. De Padova, C. Quaresima, J. Avila, E. Frantzeskakis, M. C. Asensio, A. Resta, B. Ealet and G. Le Lay, Phys. Rev. Lett., 2012, 108, 155501.
19. Y. Zheng, J. Liu, J. Liang, M. Jaroniec and S. Z. Qiao, Energy Environ. Sci., 2012, 5, 6717–6731.
20. X. Wang, X. Chen, A. Thomas, X. Fu and M. Antonietti, Adv. Mater., 2009, 21, 1609–1612.
21. Y. Wang, Y. Di, M. Antonietti, H. Li, X. Chen and X. Wang, Chem. Mater., 2010, 22, 5119–5121.
22. E. Perim and D. S. Galvao, ChemPhysChem, 2014, 15, 2367–2371.
23. J. Li, C. Cao and H. Zhu, Nanotechnology, 2007, 18, 115605.
24. Y. Zhao, D. Yu, H. Zhou, Y. Tian and O. Yanagisawa, J. Mater. Sci., 2005, 40, 2645–2647.
25. D. Wei, Y. Liu, Y. Wang, H. Zhang, L. Huang and G. Yu, Nano Lett., 2009, 9, 1752–1758.
26. M. Zelisko, Y. Hanlumyuang, S. Yang, Y. Liu, C. Lei, J. Li, P. M. Ajayan and P. Sharma, Nat. Commun., 2014, 5, 4284.
27. G. Algara-Siller, N. Severin, S. Y. Chong, T. Björkman, R. G. Palgrave, A. Laybourn, M. Antonietti, Y. Z. Khimyak, A. V. Krasheninnikov and J. P. Rabe, Angew. Chem., 2014, 126, 7580–7585.
28. A. Thomas, A. Fischer, F. Goettmann, M. Antonietti, J.-O. Müller, R. Schlögl and J. M. Carlsson, J. Mater. Chem., 2008, 18, 4893–4908.
29. E. Kroke, M. Schwarz, E. Horath-Bordon, P. Kroll, B. Noll and A. D. Norman, New J. Chem., 2002, 26, 508–512.
30. B. V. Lotsch, M. Döblinger, J. Sehnert, L. Seyfarth, J. Senker, O. Oeckler and W. Schnick, Chemistry, 2007, 13, 4969–4980.
31. M. Döblinger, B. V. Lotsch, J. Wack, J. Thun, J. Senker and W. Schnick, Chem. Commun., 2009, 1541–1543.
32. F. Cui and D. Li, Surf. Coat. Technol., 2000, 131, 481–487.
33. M. Deifallah, P. F. McMillan and F. Corà, J. Phys. Chem. C, 2008, 112, 5447–5453.
34. S.-D. Mo, L. Ouyang, W. Ching, I. Tanaka, Y. Koyama and R. Riedel, Phys. Rev. Lett., 1999, 83, 5046.
35. J. Budzien, A. P. Thompson and S. V. Zybin, J. Phys. Chem. B, 2009, 113, 13142–13151.
36. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
37. A. C. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 9396–9409.
38. G. J. Martyna, M. E. Tuckerman, D. J. Tobias and M. L. Klein, Mol. Phys., 1996, 87, 1117–1157.
39. A. Nair, S. Cranford and M. Buehler, EPL, 2011, 95, 16002.
40. S. W. Cranford and M. J. Buehler, Carbon, 2011, 49, 4111–4121.
41. A. P. Garcia and M. J. Buehler, Comput. Mater. Sci., 2010, 48, 303–309.
42. T. Botari, E. Perim, P. Autreto, A. C. van Duin, R. Paupitz and D. Galvao, Phys. Chem. Chem. Phys., 2014, 16, 19417–19423.
43. B. D. Jensen, K. E. Wise and G. M. Odegard, J. Comput. Chem., 2015, 36, 1587–1596.
44. J. M. de Sousa, G. Brunetto, V. R. Coluci and D. S. Galvao, Carbon, 2016, 96, 14–19.
45. B. Mortazavi, G. Cuniberti and T. Rabczuk, Comput. Mater. Sci., 2015, 99, 285–289.
46. F. Liu, P. Ming and J. Li, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 064120.

---