DOI:
10.1039/C6RA13878K
(Paper)
RSC Adv., 2016,
6, 115354-115363
Molecular dynamics simulation of a LixMn2O4 spinel cathode material in Li-ion batteries
Received
28th May 2016
, Accepted 12th November 2016
First published on 25th November 2016
Abstract
In this study molecular dynamics simulations and a particle-level mathematical model were used to study the state of charge (SOC) dependent mechanical properties such as yield stress, ultimate stress and Young’s modulus of lithium manganese oxide as a cathode material in Li-ion batteries during electrochemical cycling. The molecular model was applied on a unit cell of LiMn2O4, containing 56 ions (8 lithium ions, 8 trivalent manganese ions, 8 tetravalent manganese ions and 32 oxygen atoms) that was replicated in 2 × 2 × 2 cubic structure. The volume changes of LixMn2O4 was investigated as a function of the SOC (0 < x < 1). MD simulations indicated that the lattice volume of LixMn2O4 varied by 6.87% in one half cycle. This large volume change was attributed to lithium compositional changes during electrochemical cycling. MD simulations showed that at low SOC values LixMn2O4 behaves as a brittle material and at high SOC values behaves as a ductile material. Furthermore, due to the existence of two phase of LixMn2O4 in the range of low SOC values, we observed that the elastic properties increase as the SOC decreases from 0.375 to 0. By employing visualization techniques it was clear that the LiMn2O4 fracture process is initiated by void formation in a nearby material’s surface and consequently leads to surface fracture. Using long MD simulations, mean square displacement (MSD) calculations indicated that there are three different regimes in the MSD curves: ballistic, caging and diffusive. Also the SOC-dependent Li ion diffusion coefficients were investigated and revealed that due to the greater availability of vacant sites at low SOC values the Li ion diffusion coefficient is higher than at high SOC values.
1 Introduction
In recent years development of LiMn2O4 spinel oxides as an electrode material for Li-ion batteries has been of considerable interest in this research area. In fact, due to its low toxicity, low cost, high operating voltage and high energy density,1,2 this material is preferred over lithium cobalt oxide and lithium nickel oxide. However this material has some drawbacks and one of the most important of them is large volume changes in the charging and discharging operation of the battery.3 These volume changes in the electrochemical cycles induce a special type of stress in the LixMn2O4 structure which is referred to as “electrochemical shock” by Woodford and his co-workers.4 Electrochemical shock will result in fracture phenomena in the electrode’s active material and finally these fractures result in mechanical damage to the electrode and accelerate dissolution of the active electrode material. These processes over several electrochemical cycles will degrade the battery’s performance and life span.5,6
However in research work performed by Woodford and his co-workers,4,7 electrochemical shock in intercalation materials such as LiMn2O4, has been studied extensively. They have presented three different electrochemical shock mechanisms that can be the cause of fracturing of the electrode materials: (1) diffusion-induced, (2) phase transformation (two-phase coherency) and (3) anisotropic microfractures. They also present a practical and useful classification for these electrochemical shock mechanisms according to C-rate sensitivity. Their observations have shown that only the diffusion-induced mechanism is C-rate sensitive and becomes important at high C-rates. In the case of LiMn2O4 as an intercalation material, due to the cubic structure and isotropic Vegard coefficient the third mechanism, anisotropic microfracture, is not active but the second mechanism, two phase coherency stresses, can be active over some composition ranges where LixMn2O4 has two solid solution phases. In a computational study, Lee and his co-workers2 have shown that LixMn2O4, has two phases over a range of 0.25 < x < 0.5. In all intercalation materials such as LiMn2O4, diffusion-induced electrochemical shock is active especially at high C-rates.7
The molecular dynamics (MD) method has been used widely to investigate the mechanical and diffusive properties of ion-intercalation materials.1,2,8–17 In the case of LiMn2O4 as an ion-intercalation material, Lee et al. have used MD simulations to study the state of charge (SOC) dependent elasticity of LixMn2O4.2 They did not consider the C-rate (strain rate) effect in their MD deformation simulation, when the strain rate influence on mechanical properties must be considered in such studies. Another aspect of any ion-intercalation material is the diffusive properties of all species in the system. Extensive efforts have been devoted to study lithium and manganese diffusion in the LiMn2O4 system.8,18–20 Kumar et al., in a multi-scale simulation study, used a macroscopic model and an atomic-scale model in order to investigate the transport properties and stress analysis of LixMn2O4 and LiC6 as cathode and anode materials in Li-ion batteries.20 The objective of this study is to investigate the SOC-dependent mechanical properties, fracture behaviour and ion diffusion of LixMn2O4 as an electrode material from a molecular point of view. In order to reach these goals we employed an atomic-scale model, a particle-level mathematical model4 and Vegard coefficients concept.21
This paper is organized as follows: in Section 2.1 the MD simulation setup and procedure are described. In Section 2.2 a particle-level model developed by Woodford et al. is employed to find the C-rate effect on the rate of Li concentration change in electrochemical cycling. In Section 3.1 we provide a series of results in order to validate the molecular model. In Section 3.2, the results of the deformation simulation and mechanical properties are presented. In Section 3.3, ion diffusion properties of LiMn2O4 are presented.
2 Simulation methods
2.1 MD simulation
In this MD study, the interatomic interactions are described by the Gilbert-Ida-type pair potential function represented by:| |  | (1) |
In eqn (1), the first term represents electrostatic interactions and the second term represents short range van der Waals interactions. Zi is the effective atomic charge of atom i, e is the elementary electric charge, rij is the interatomic distance between atoms i and j, f0 is a constant number (f0 = 4.184 kJ−1 mol−1), ai is the atomic radius of atom i and bi is the atomic compressibility parameter of atom i. Numerical values of these parameters reported by Suzuki et al.18 are listed in Table 1. The Ewald method is used for computing the long-range coulombic interactions.
Table 1 Potential function parameters2
| Ions |
Z
i
|
a
i
|
b
i
|
| Li+ |
+1.0 |
1.043 |
0.080 |
| Mn3+ |
+1.4 |
1.038 |
0.070 |
| Mn4+ |
+2.4 |
0.958 |
0.070 |
| O2− |
−1.2 |
1.503 |
0.075 |
The unit cell of LiMn2O4, contains 56 ions (8 lithium ions, 8 trivalent manganese ions, 8 tetravalent manganese ions and 32 oxygen atoms) and these atoms are located in a cubic structure in the Fd3m space group. The atomic coordinates of these 56 particles were taken from a study performed by Sickafus and his co-workers.22 The cutoff distance for pair interactions is set to 10 Å which is greater than the size of one unit cell, 8.24 Å, therefore at least two unit cells are needed for the MD simulations. On the other hand, increasing the size of the simulation box applies extra computational load that is not necessary. For these reasons a 2 × 2 × 2 simulation box was used in this study. The unit cell of LiMn2O4 and 2D and 3D views of the simulation box are shown in Fig. 1.
 |
| | Fig. 1 The structure of LiMn2O4: (a) the unit cell of LiMn2O4 (front-half), (b) 2D view of the MD simulation box, (c) 3D view of the MD simulation box, red: Li+, blue: Mn3+, yellow: Mn4+, white: O2−. | |
Structural optimization was carried out using the Polack–Ribiere conjugate gradient (PRCG) method.23 All MD simulations in this study were performed using the LAMMPS MD package which is a classical molecular dynamics code, and an acronym for Large-scale Atomic/Molecular Massively Parallel Simulator.24 In these simulations the NPT and NVT ensembles were used during the equilibration and production phases. For the NPT ensemble, the number of particles N and the pressure and temperature of the system P and T are kept constant. For the NVT ensemble, the number of particles N and the volume and temperature of the system V and T are kept constant. A Nose–Hoover thermostat25,26 was used to regulate the system’s temperature at specific temperatures. The time step was set to 1 fs and periodic boundary conditions were used in the x, y and z directions. In our MD simulations the Li ion elimination technique was employed. The LixMn2O4 structure was simulated in nine different states of charge (SOC) (x = 1, 0.875, 0.750, 0.625, 0.5, 0.375, 0.25, 0.125, 0). The SOC is defined as the lithium concentration in the LixMn2O4 structure that is denoted by x. With the elimination of each Li ion from the spinel structure, one Mn3+ ion switches to Mn4+ ion in order to maintain system neutrality. As an example, with elimination of the first Li ion from the LiMn2O4 structure, the SOC will be 0.875 and the number of Li ions in the structure is 7 and the number of available sites for these Li ions is 8, therefore, the Li ions have 8 possible states when located in the LixMn2O4 lattice structure. On the other hand, the number of Mn3+ ions is 7 and the number of available sites for these ions is 16, therefore the Mn3+ ions have 128 possible states when located in the structure. Using this procedure, we can evaluate the total number of possible crystal structures for each SOC. Results of these calculations are listed in Table 2.
Table 2 The possible configurations of LixMn2O4 at each SOC
| SOC |
Number of Li-ions |
Possible configurations |
| 0 |
0 |
1 |
| 0.125 |
1 |
128 |
| 0.250 |
2 |
3360 |
| 0.375 |
3 |
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 360 360 |
| 0.500 |
4 |
127![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 400 |
| 0.625 |
5 |
244![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 608 608 |
| 0.750 |
6 |
224![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 224 224 |
| 0.875 |
7 |
91![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520 520 |
| 1.000 |
8 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 870 870 |
In order to reduce the computational time, we use one step MD simulations to specify the potential energy of all possible structures and the structures with minimum potential energy. As shown in Fig. 2, we use a MATLAB® script file to generate about 700![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 possible initial structures for the one step MD simulations. MATLAB® is a high-performance language for technical computing, visualization, and programming.
000 possible initial structures for the one step MD simulations. MATLAB® is a high-performance language for technical computing, visualization, and programming.
 |
| | Fig. 2 MATLAB-LAMMPS linking for running one step MD simulations on all possible structures. | |
Initial simulations were performed at 300 K and atmospheric pressure using the NPT ensemble. These simulations consist of two phases: equilibration and production. The equilibration phase was a simulation for 20 ps. In the production phase, the system was simulated for 30 ps in order to find the final structure of LiMn2O4 at each SOC. In the next stage long NVT simulations were performed at various temperatures (i.e. 300 K, 600 K, 1000 K, 2000 K, 2500 K and 3000 K) for 1–2 ns in order to calculate the mean square displacement (MSD) of all species in the system. The long MD simulations are necessary for understanding the ion dynamics in the LiMn2O4 spinel structure. In the final stage of our study, in order to investigate the mechanical properties of the LiMn2O4 at various SOC values, deformation simulations were performed using the NPT ensemble at 300 K for 50 ps. In the deformation simulations, the system was deformed under uniaxial strain (i.e. compositional strain) applied at different strain rates. These strain rates correspond to different operational C-rates in Li-ion batteries. In Section 2.2 we use a particle-level model for establishing the connection between the applied strain rates and operational C-rates. To evaluate the stress–strain relationship we use an atomic-level stress tensor in the form of the virial stress. That is expressed as follows:27
| |  | (2) |
where
i and
j are the atomic indices,
Ω is the total volume,
mi is the mass of atom
i,
![[u with combining dot above]](https://www.rsc.org/images/entities/b_i_char_0075_0307.gif) i
i is the displacement vector of atom
i relative to a reference position,
rij =
ri −
rj, and
fij is the interatomic force applied on atom
i by atom
j.
2.2 Particle-level simulation
In this work we study the mechanical properties of LiMn2O4 during the charging and discharging processes, therefore the operational C-rate should be considered as an important parameter in MD simulations. The C-rate parameter describes the charging rate of the lithium-ion cell and has units of h−1. To determine the strain rate equivalent to each C-rate in the MD deformation simulations, we used a particle-level model that was developed by Woodford et al.4 This model starts with a diffusion equation that describes the electrochemical cycling of the cathode particle.| |  | (3) |
where X is the lithium composition which is normalized to take values 0 ≤ X ≤ 1, and J is the flux which is proportional to the gradient of the diffusion potential Φ
The diffusion potential, Φ, can be represented by
| |  | (5) |
By substituting eqn (5) into (4) the diffusion equation can be expressed as
| |  | (6) |
where
D(
X) is the chemical-diffusivity of lithium ions that is defined as
4| |  | (7) |
Table 3 lists values of the model parameters for LiMn2O4 as an active cathode material. For numerical calculations we use a dimensionless form of the above equations by normalizing all lengths to the particle radius, r, and defining dimensionless variables:
| |  | (8) |
| |  | (9) |
Table 3 The required parameters of the particle-level model for LiMn2O4 (ref. 4)
| Property |
Symbol |
Unit |
Value |
| Young’s modulus |
E
|
GPa |
200 |
| Poisson’s ratio |
ν
|
— |
0.3 |
| Lithium diffusivity |
D
|
cm2 s−1 |
2.2 × 10−9 |
| Partial molar volume of lithium |
Ω
|
cm3 mol−1 |
3.26 |
| Maximum lithium concentration |
c
max
|
mol m−3 |
2.37 × 104 |
| Density |
ρ
|
g cm−3 |
2.37 × 104 |
| Theoretical capacity |
α
|
mA h g−1 |
148 |
Based on these dimensionless variables, the boundary conditions are
| | 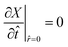 | (10) |
| |  | (11) |
where the dimensionless current,
I, is expressed as follows:
| |  | (12) |
In the last equation α is the theoretical charge capacity, ρ is the particle density, cmax is the maximum lithium concentration, F is the faraday constant and the D0 is the lithium diffusivity coefficient. Because of the chemo-mechanical nature of a Li-ion battery, there are interconnections between the mechanical and chemical aspects of any intercalation material such as LiMn2O4 that are shown in Fig. 3. In the next step the Vegard relation that is expressed21,28 as eqn (13), will be used to determine the applied strain rates.
 |
| | Fig. 3 The interconnections between mechanical and chemical aspects of any intercalation material. The relation between concentration, c, and strain, ε, can be represented by the Vegard relation. | |
ε
c represents the compositional strain and βij are the Vegard coefficients. Because of the cubic structure of LiMn2O4, it has isotropic Vegard coefficients.7 Therefore all Vegard coefficients are considered the same and equal to 0.016 based on Chung et al.’s report.21
3 Results and discussion
3.1 Validation
The calculated lattice parameter for LiMn2O4, is 8.22 Å, which is in good agreement with the value of 8.24 Å which was reported previously in experimental work.29–31 In Table 4 these experimental values are listed. For each SOC, the value of the equilibrium lattice constant was calculated and the results are shown in Fig. 4. Based on this figure it is clear that the equilibrium lattice constant in the charging process (i.e. a lithium concentration decrease) decreases. This trend is in good agreement with experimental observations.32,33 The lattice constant at x = 1 is 8.22 Å and decreases to 8.04 Å at x = 0 in one electrochemical half-cycle. Therefore the volume change of the spinel structure is 6.87%, and is in good agreement with other work.2,34 The equilibrium structure of LiMn2O4 was investigated using the radial distribution function (RDF), g(r), that describes the spatial arrangement of ions about a central ion in the LiMn2O4 lattice using the following equation:| | 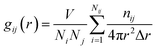 | (14) |
where Ni and Nj are the number of ions in the unit cell, V is the volume of the unit cell, nij is the number of ions in the spherical shell between radius r and radius r + Δr centered on the ion, i. The results of the RDF analysis at 300 K are shown in Fig. 5. It can be seen that both curves have one sharp peak corresponding to the first nearest neighbor shell. The average interatomic distances are 2.00 Å and 1.8 Å for the Mn3+–O and Mn4+–O bonds respectively, and are in good agreement with computational and experimental studies carried out by Ishizawa and Tateishi and their co-workers.19,29 Furthermore, Fig. 6a–c indicates that the Mn ions migrate slightly from their 16d sites, and this phenomena also has been reported by Suzuki et al.18
Table 4 The calculated lattice constants of LiMn2O4 and λ-MnO2 and a comparison with their experimental values
| |
Calculated |
Experimental29–31 |
| LiMn2O4 |
8.22 |
8.24 |
|
λ-MnO2 |
8.04 |
8.05 |
 |
| | Fig. 4 Equilibrium lattice constant of LiMn2O4 at different SOC values. | |
 |
| | Fig. 5 Radial distribution function of the Mn3+–O and Mn4+–O interactions at 300 K. | |
 |
| | Fig. 6 Radial distribution function of the Mn–Mn interactions at two different SOC values at 300 K: (a) Mn3+–Mn3+, (b) Mn3+–Mn4+ and (c) Mn4+–Mn4+. | |
3.2 Mechanical properties
To investigate the SOC-dependent mechanical properties of LiMn2O4, we performed a series of room temperature uniaxial deformation MD simulations at 6 different SOC values (i.e. x = 1, 0.625, 0.5, 0.375, 0.25, and 0) and various strain rates. In Fig. 7, the result of the particle-level simulation is shown. In this figure there is a plateau between the dimensionless time of 5–20 for low rates of <2C. In fact the double-well shape of chemical diffusivity D(X)7 clearly affects the dimensionless Li-ion concentration drop inside the particle ΔX(t). During the electrochemical charge cycle, initially the dimensionless Li-ion concentration drop increases, then depending on the operational C-rate, decreases to a lower value (a plateau) and finally increases again to a maximum. Woodford et al.7 showed that the decrease in the dimensionless Li-ion concentration drop at intermediate times happens when the Li composition (SOC) is X ≈ 0.6, where the chemical diffusivity D(X) is locally maximized. This pattern was also reported by Bohn et al.35 It can be seen from this figure that the rate of the Li-ion concentration drop from the particle surface toward the particle center is increased as the C-rate increased. Based on these results and employing the Vegard relation, the average values of the lithium composition change rate at different C-rates and the values of strain rates corresponding to each C-rate, are listed in Table 5.
 |
| | Fig. 7 Lithium composition profile at particle surface at different C-rates. | |
Table 5 The average of the lithium composition change rate at different C-rates and corresponding strain rates for use in MD simulations
| C-rate (h−1) |

|
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c (ps−1)
c (ps−1) |
| 0.5C |
0.04 |
0.001 |
| 1C |
0.08 |
0.002 |
| 2C |
0.16 |
0.004 |
| 5C |
0.40 |
0.010 |
| 10C |
0.80 |
0.020 |
Fig. 8 illustrates the tensile stress–strain curves. According to this figure, it is obvious that the yield and ultimate stress values are strongly dependent on the SOC (i.e. x in LixMn2O4). For further insight into the ductility and brittleness of the LiMn2O4 system during electrochemical operation, we focus on the yield point that denotes the stage after which plastic deformation starts and the ultimate tensile strength that denotes the maximum stress value in the stress–strain curve. Fig. 8 indicates that at high SOC values (the beginning of the battery charging operation), LixMn2O4 behaves as a ductile material and at low SOC values (the end of the battery charging operation), LixMn2O4 behaves as a brittle material and does not show plastic behaviour, so in the stress strain curve, the breaking point of the ultimate tensile stress occurs immediately after the elastic limit end. Therefore for brittle states of LixMn2O4 the yield stress is equal to the ultimate tensile stress. Fig. 9 illustrates the SOC-dependent mechanical properties of the LixMn2O4 system at three different strain rates of 4 × 10−3 ps−1, 10 × 10−3 ps−1 and 20 × 10−3 ps−1. This figure indicates that as the SOC decreases from 1 to 0.375 the yield and ultimate stresses also decrease and as the SOC decreases from 0.375 to 0 the yield and ultimate stresses increase. In order to gain further insight into this pattern, we refer to the Lee et al.’s paper.2 As discussed in their report, the mechanical properties of LiMn2O4 are generally composed of three terms: the kinetic energy contribution, the long-range coulombic interactions and the pair interactions. They also concluded that the kinetic energy contribution and long-range coulombic interactions do not change during the electrochemical charge cycle. In fact, the only responsible phenomenon for the mechanical properties’ changes during electrochemical cycling is pair-interactions. There are 10 types of pair-interactions in the LiMn2O4 system: Li+–Li+, Li+–Mn3+, Li+–Mn4+, Li+–O2−, Mn3+–Mn3+, Mn3+–Mn4+, Mn3+–O2−, Mn4+–Mn4+, Mn4+–O2− and O2−–O2−. During electrochemical cycling (Li-ion insertion and extraction), the amounts of these ions (Li+, Mn3+ and Mn4+) change and consequently the pair-interactions also change. These variations determine the pattern of the mechanical properties’ changes. In Fig. 9, the increase of stresses at low SOC values, can be due to the two phases’ coherency stresses as one of the three electrochemical shock mechanisms that are mentioned in Section 1 and reported by Woodford et al.4,7 The existence of two phases of LixMn2O4 over the range of low SOC values has also been reported by Lee et al.2 The calculated lattice constants of LiMn2O4 at different SOC values in their work indicated that there are lattice constant fluctuations in the range of 0.25 < SOC < 0.5. Also there are studies about lattice constant criterion for miscibility gaps in any solid solution.36,37 These studies imply that fluctuations of lattice constant will be interpreted as a sign of two phase co-existence. Therefore, in the case of LiMn2O4 as an ion-intercalation material, there is a two phase region in the range of 0.25 < SOC < 0.5. Woodford and his co-workers7 also reported this hypothesis.
 |
| | Fig. 8 Stress–strain curves for different SOC values at three strain rates (a) 4 × 10−3 ps−1 (2C), (b) 10 × 10−3 ps−1 (5C) and (c) 20 × 10−3 ps−1 (10C). | |
 |
| | Fig. 9 Yield stress (a) and ultimate stress (b) values as a function of SOC at three different strain rates (C-rates) 4 × 10−3 ps−1 (2C), 10 × 10−3 ps−1 (5C) and 20 × 10−3 ps−1 (10C). | |
Another point that we notice from Fig. 8 is that the strain rate is independent of the elastic properties of the LixMn2O4 system. Furthermore, Fig. 10 illustrates that for the LiMn2O4 system (SOC = 1) at different strain rates, the stress profile increases linearly up to about 20 GPa, which is the yield stress. This figure confirms that the yield stress, ultimate stress and the Young’s modulus (E) of LiMn2O4 is independent of the strain rate but as is shown in Fig. 8, the Young’s modulus is considerably dependent on the SOC, which is also reported by Lee et al.2 By employing the linear regression method on the elastic region of the stress–strain curves, we calculate the SOC-dependent Young’s modulus of LixMn2O4 that is in good agreement with reported values by Lee et al.2 In Fig. 11 the result of the Young’s modulus calculations is shown.
 |
| | Fig. 10 Stress–strain curve of LiMn2O4 under uniaxial tensile strain at different strain rates (different C-rates). The C-rate independence of the elastic properties can be seen. | |
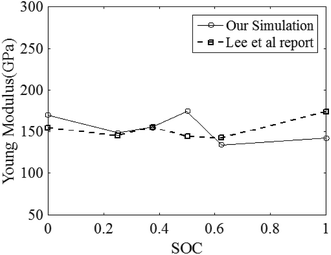 |
| | Fig. 11 Calculated Young’s modulus E of LixMn2O4 as a function of the SOC. | |
An investigation of fracture behaviour of LiMn2O4 was carried out by considering a 5 × 5 × 5 simulation box in order to observe the fracture process clearly. Fig. 12 illustrates the atomic model situation at different strains. As can be seen that a fracture is initiated with void formation followed by necking and finally surface fracture occurs.
 |
| | Fig. 12 A snapshot of the atomic configuration of LiMn2O4 at 300 K upon tensile loading at several strain values: (a) elastic behaviour at low strains, (b) formation of voids at higher strains and fracture initiation, (c) necking and subsequent surface fracture. The red, blue, yellow and white particles represent Li, Mn3+, Mn4+ and O respectively. | |
3.3 Ion diffusion
In order to investigate the diffusion properties of all ionic species and the effect of Li-ion concentration (i.e. SOC) and temperature on the diffusivity of the Li-ion in the LiMn2O4 cathode material, the mean square displacement (MSD) of all particles was calculated using the following formula:9,19| | 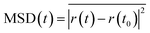 | (15) |
where the overline represents the average over all of the species of the same type in the simulation box, r(t) represents the atom coordinates at time, t, and t0 is the original position at t = t0. By post-processing the direct simulation results, the Li-ion trajectories were investigated and have been shown in Fig. 13a, these trajectories confirm that the migration of lithium ions in LixMn2O4 is through 3-D pathways. This result has also been reported by many researchers.29,38,39 Further investigations into the diffusive behavior of Mn and O showed that these species have no diffusive behavior and only vibrate around their original positions. This behavior has been shown in Fig. 13b and c and also reported by Ouyang et al.8
 |
| | Fig. 13 3D trajectory plots of all ionic species in the LiMn2O4 spinel structure. (a) The migration of Li-ions through 3D-pathways. This view reveals the existence of 3-D channels for Li-ion migration in electrochemical cycling. (b and c) Mn and O species do not have diffusive behavior inside the spinel structure and only vibrate around their original positions. | |
An ion-intercalation material as a cathode material in a real battery at its operational temperature is subjected to voltage and reduction-oxidation effects, therefore there are faster diffusion rates in an active cathode material than we obtain in an MD simulation at the same temperature. Nevertheless the MD simulation can be considered to be a test for comparative material performance. For the MSD and diffusivity coefficient study, duo to computationally restricted MD calculations, simulations were performed at elevated temperatures. The diffusion coefficient of Li ions can be obtained from the MSD data by the Einstein relation as follows:
| |  | (16) |
As can be seen in Fig. 14, the MSD calculations reveal that there is no Li ion diffusion for LixMn2O4 in the fully discharged state (i.e. x = 1) because in this stoichiometric composition there is no available vacant site for Li ion diffusion but at the SOC = 0.875 diffusion of the Li ions clearly occurs. Due to having simulations as long as 2 ns, three regimes can be seen in the MSD curves: ballistic, caging and diffusive. In short time periods the Li ions hop by ballistic motion: this is the so called ballistic regime. After this, the caging regime is due to presence of Mn and O ions where the Li ions are trapped in their original sites and only vibrate. Finally in the diffusive regime, which occurs in nano-scale time periods, the Li ions can migrate freely to the neighboring positions, as shown in Fig. 15. For the SOC = 0.5 the calculated MSDs of the Li ions at various elevated temperatures are presented in Fig. 16 over a short time period of 40 ps for better illustration. In order to evaluate the Li ion diffusivity coefficients at room temperature for various SOC values, the Arrhenius relation was used as below:
| | D = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ea/kBT) exp(−Ea/kBT) | (17) |
where
Ea is the activation energy,
A is the prefactor,
kB is the Boltzmann constant and
T is the temperature. Assuming the identical diffusion mechanism at lower and elevated temperatures, the room temperature diffusion coefficient can be determined by extrapolation of the Arrhenius plot to room temperature. The Arrhenius plots (ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D vs.
D vs. 1/
T) for different SOC values are shown in
Fig. 17. For the SOC = 0.125 (Li-poor state), SOC = 0.875 (Li-rich state) and SOC = 0.5, the calculated diffusion coefficients at 300 K are summarized in
Table 6.
 |
| | Fig. 14 Mean square displacement (MSD) plot of Li ions at 600 K for a SOC = 1 (LiMn2O4) and SOC = 0.875 (LixMn2O4, x = 0.875). It can be seen clearly that the Li ions’ diffusion does not occur in a fully discharged state (SOC = 1). | |
 |
| | Fig. 15 Mean square displacement (MSD) plot of Li ions in LixMn2O4 (x = 0.875) for 2 ns at 600 K. | |
 |
| | Fig. 16 MSD plots of Li in LixMn2O4 (x = 0.5) at several elevated temperatures for diffusion coefficient calculations (a short time period is used for better illustration). | |
 |
| | Fig. 17 The Arrhenius plots (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D vs. 1/T) of Li ion diffusion coefficients for different SOC values obtained from the MSD calculations. D vs. 1/T) of Li ion diffusion coefficients for different SOC values obtained from the MSD calculations. | |
Table 6 The calculated Li ion diffusion coefficients in LixMn2O4 as a function of SOC (i.e. x) at 300 K
| SOC |
Li ion diffusion coefficient (cm2 s−1) |
| 0.125 |
1.69 × 10−8 |
| 0.5 |
9.26 × 10−9 |
| 0.875 |
5.08 × 10−9 |
The results of Fig. 17 and Table 6 imply that at low SOC values, due to much availability of vacant sites, Li ion diffusion occurs with greater ease. This conclusion about the SOC-dependent Li ion diffusivity in the LixMn2O4 spinel structure has been reported by other researchers.20,40 From Fig. 17 it is evident that at lower temperatures, the Li ion diffusion coefficient is more dependent on the SOC.
4 Conclusions
In this study a series of molecular dynamics simulations were performed to investigate the SOC-dependent mechanical and diffusion properties of a LiMn2O4 active cathode material. Initially we calculated the lattice constant of LixMn2O4 as a function of the SOC using MD simulations. The lattice constant of LixMn2O4 was calculated to be 8.04 Å for x = 0 and 8.22 Å for x = 1. As the state of charge changes, the lattice constant and volume of the LixMn2O4 structure changes by 2.23% and 6.87% respectively at one half cycle.
From the stress–strain analysis, it can be concluded that during electrochemical cycling decreasing the SOC from 1 to 0.375 leads to a decrease in the elastic properties, but with a further decrease in the SOC from 0.375 to 0, the elastic properties increase, possibly due to the existence of two phases of LixMn2O4 at low SOC values that induce coherency stresses on LixMn2O4. Our simulation results indicate that the SOC-dependence of elastic properties of LixMn2O4 must be considered in any microscopic or macroscopic Li-ion battery simulation study. Further investigation are required on the existence of the two phases of the LixMn2O4 crystalline material at low SOC values and on the two phases of coherency stresses induced on LixMn2O4 as an intercalation material during electrochemical cycling. In the last section of this work we investigated the diffusion properties of LixMn2O4 by performing long MD simulations. It was confirmed that Li ion migration occurs through 3D channels and also Mn and O ions does not diffuse and only vibrate around their original sites. Another point about the LixMn2O4 system is the existence of three different regimes in the MSD curves that was revealed by performing MD simulations for as long as 2 ns. The effect of the SOC on diffusive behavior was investigated and it can be concluded that at low SOC values the diffusion rate is higher than at high SOC values. The SOC dependence of Li ion diffusivity, especially at lower temperatures such as room temperature, implies that in order to gain accurate results in macroscopic modeling of Li-ion batteries, the Li ion diffusion coefficients must be considered as a function of lithium concentration (i.e. SOC).
Nomenclature
|
x
| Lithium content in LiMn2O4 structure or SOC |
|
X
| Dimensionless lithium concentration (—) |
|
a
| Lattice constant of LiMn2O4 (Å) |
|
Z
i
| Effective charge of atom i (—) |
|
a
i
| Atomic radius of atom i (Å) |
|
b
i
| Atomic compressibility parameter of atom i (—) |
|
r
ij
| Distance between atoms i and j (Å) |
|
E
| Young’s modulus (GPa) |
|
ν
| Poisson’s ratio (—) |
|
D
| Lithium diffusivity (m2 s−1) |
|
Ω
| Partial molar volume of lithium (m3 mol−1) |
|
c
max
| Maximum lithium concentration (mol m−3) |
|
ρ
| Density (kg m−3) |
|
α
| Theoretical charge capacity (A h kg−1) |
|
F
| Faraday constant (A s mol−1) |
|
t
| Time (s) |
![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif)
| Dimensionless time (—) |
|
r
| Radial position (m) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif)
| Dimensionless radial position (—) |
|
Î
| Dimensionless current (—) |
|
V(X) | Open-circuit voltage (V vs. Li+/Li) |
|
σ
c
| Compositional stress (GPa) |
|
ε
c
| Compositional strain (—) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c
c
| Rate of compositional strain (ps−1) |
References
- M. Nakayama, M. Kaneko, Y. Uchimoto, M. Wakihara and K. Kawamura, J. Phys. Chem. B, 2004, 108, 3754–3759 CrossRef CAS.
- S. Lee, J. Park, A. M. Sastry and W. Lu, J. Electrochem. Soc., 2013, 160, A968–A972 CrossRef CAS.
-
Z. Zhang and S. Zhang, Rechargeable Batteries: Materials, Technologies and New Trends, Springer International Publishing, 2015 Search PubMed.
- W. H. Woodford, Y.-M. Chiang and W. C. Carter, J. Electrochem. Soc., 2010, 157, A1052–A1059 CrossRef CAS.
- K. An, P. Barai, K. Smith and P. P. Mukherjee, J. Electrochem. Soc., 2014, 161, A1058–A1070 CrossRef CAS.
- C.-F. Chen, P. Barai and P. P. Mukherjee, J. Electrochem. Soc., 2014, 161, A2138–A2152 CrossRef CAS.
- W. H. Woodford, Y.-M. Chiang and W. C. Carter, J. Electrochem. Soc., 2013, 160, A1286–A1292 CrossRef CAS.
- C. Y. Ouyang, S. Q. Shi, Z. X. Wang, H. Li, X. J. Huang and L. Q. Chen, Europhys. Lett., 2004, 67, 28 CrossRef CAS.
- P. Zhang, Y. Wu, D. Zhang, Q. Xu, J. Liu, X. Ren, Z. Luo, M. Wang and W. Hong, J. Phys. Chem. A, 2008, 112, 5406–5410 CrossRef CAS PubMed.
- S. C. Jung and Y.-K. Han, Electrochim. Acta, 2012, 62, 73–76 CrossRef CAS.
- R. Fallahzadeh and N. Farhadian, Solid State Ionics, 2015, 280, 10–17 CrossRef CAS.
- M. M. Islam, A. Ostadhossein, O. Borodin, A. T. Yeates, W. W. Tipton, R. G. Hennig, N. Kumar and A. C. T. van Duin, Phys. Chem. Chem. Phys., 2015, 17, 3383–3393 RSC.
- K. Sau and P. P. Kumar, J. Phys. Chem. C, 2015, 119, 1651–1658 CAS.
- H. Wang and H. B. Chew, Extreme Mechanics Letters, 2016, 9, 503–513 CrossRef.
- M. T. McDowell, S. Xia and T. Zhu, Extreme Mechanics Letters, 2016, 9, 480–494 CrossRef.
- R. S. Ledwaba, M. G. Matshaba and P. E. Ngoepe, IOP Conf. Ser.: Mater. Sci. Eng., 2015, 80, 012024 CrossRef.
- S. Lee and S. S. Park, J. Phys. Chem. C, 2012, 116, 25190–25197 CAS.
- K. Suzuki, Y. Oumi, S. Takami, M. Kubo, A. Miyamoto, M. Kikuchi, N. Yamazaki and M. Mita, Jpn. J. Appl. Phys., 2000, 39, 4318 CrossRef CAS.
- K. Tateishi, D. du Boulay, N. Ishizawa and K. Kawamura, J. Solid State Chem., 2003, 174, 175–181 CrossRef CAS.
- U. Kumar, A. K. Metya, N. Ramakrishnan and J. K. Singh, J. Electrochem. Soc., 2014, 161, A1453–A1460 CrossRef CAS.
- D.-W. Chung, P. R. Shearing, N. P. Brandon, S. J. Harris and R. E. Garcia, J. Electrochem. Soc., 2014, 161, A422–A430 CrossRef CAS.
- K. E. Sickafus, J. M. Wills and N. W. Grimes, J. Am. Ceram. Soc., 1999, 82, 3279–3292 CrossRef CAS.
- E. Polak and G. Ribière, Rev. Franç. Inform. Rech. Opér., 1969, 3, 35–43 Search PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695 CrossRef.
- A. K. Subramaniyan and C. Sun, Int. J. Solids Struct., 2008, 45, 4340–4346 CrossRef.
- R. E. Garcia, Y.-M. Chiang, W. Craig Carter, P. Limthongkul and C. M. Bishop, J. Electrochem. Soc., 2005, 152, A255–A263 CrossRef CAS.
- N. Ishizawa, D. du Boulay, M. Hayatsu, S. Kuze, Y. Matsushima, H. Ikuta, M. Wakihara, Y. Tabira and J. R. Hester, J. Solid State Chem., 2003, 174, 167–174 CrossRef CAS.
- Y. Xia and M. Yoshio, J. Electrochem. Soc., 1996, 143, 825–833 CrossRef CAS.
- J. Dahn, E. Fuller, M. Obrovac and U. von Sacken, Solid State Ionics, 1994, 69, 265–270 CrossRef CAS.
- K. Kanamura, H. Naito, T. Yao and Z.-i. Takehara, J. Mater. Chem., 1996, 6, 33–36 RSC.
- B. Xu and S. Meng, J. Power Sources, 2010, 195, 4971–4976 CrossRef CAS.
- Y. Qi, L. G. Hector, C. James and K. J. Kim, J. Electrochem. Soc., 2014, 161, F3010–F3018 CrossRef CAS.
- E. Bohn, T. Eckl, M. Kamlah and R. McMeeking, J. Electrochem. Soc., 2013, 160, A1638–A1652 CrossRef CAS.
- L. M. Foster, J. Electrochem. Soc., 1974, 121, 1662–1665 CrossRef CAS.
- Y. Iwamura, S. Yamamori, H. Negishi and M. Moriyama, Jpn. J. Appl. Phys., 1985, 24, L581 CrossRef.
- M. Nakayama, M. Kaneko and M. Wakihara, Phys. Chem. Chem. Phys., 2012, 14, 13963–13970 RSC.
- H. Xia, Z. Luo and J. Xie, Prog. Nat. Sci.: Mater. Int., 2012, 22, 572–584 CrossRef.
- R. T. Cygan, H. R. Westrich and D. H. Doughty, MRS Online Proc. Libr., 2011, 496, 109 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here. 

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 360
360![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400
400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 608
608![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 224
224![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520
520![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 870
870![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 possible initial structures for the one step MD simulations. MATLAB® is a high-performance language for technical computing, visualization, and programming.
000 possible initial structures for the one step MD simulations. MATLAB® is a high-performance language for technical computing, visualization, and programming.
![[u with combining dot above]](https://www.rsc.org/images/entities/b_i_char_0075_0307.gif) i is the displacement vector of atom i relative to a reference position, rij = ri − rj, and fij is the interatomic force applied on atom i by atom j.
i is the displacement vector of atom i relative to a reference position, rij = ri − rj, and fij is the interatomic force applied on atom i by atom j.






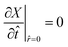



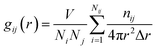




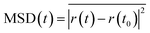

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ea/kBT)
exp(−Ea/kBT)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D vs. 1/T) for different SOC values are shown in Fig. 17. For the SOC = 0.125 (Li-poor state), SOC = 0.875 (Li-rich state) and SOC = 0.5, the calculated diffusion coefficients at 300 K are summarized in Table 6.
D vs. 1/T) for different SOC values are shown in Fig. 17. For the SOC = 0.125 (Li-poor state), SOC = 0.875 (Li-rich state) and SOC = 0.5, the calculated diffusion coefficients at 300 K are summarized in Table 6.


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D vs. 1/T) of Li ion diffusion coefficients for different SOC values obtained from the MSD calculations.
D vs. 1/T) of Li ion diffusion coefficients for different SOC values obtained from the MSD calculations.![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif)
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif)
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c
c










