A first-principles study of the avalanche pressure of alpha zirconium
Qing Peng *ab,
Wei Jia,
Jie Liana,
Fei Gaoc,
Shuming Pengd,
Hanchen Huange and
Suvranu Dea
*ab,
Wei Jia,
Jie Liana,
Fei Gaoc,
Shuming Pengd,
Hanchen Huange and
Suvranu Dea
aDepartment of Mechanical, Aerospace and Nuclear Engineering, Rensselaer Polytechnic Institute, Troy, NY 12180, USA. E-mail: qpeng.org@gmail.com
bSchool of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China
cDepartment of Nuclear Engineering and Radiological Science, University of Michigan, Ann Arbor, MI 48109, USA
dInstitute of Nuclear Physics and Chemistry, China Academy of Engineering Physics, Mianyang 621900, China
eDepartment of Mechanical and Industrial Engineering, Northeastern University, Boston, MA 02115, USA
First published on 15th July 2016
Abstract
We investigate the stability of a monovacancy in alpha zirconium under various strains and pressures by examining the vacancy formation energy through first-principles calculations. There is a maximum formation energy of 2.35 eV under uniaxial strain corresponding to a c/a ratio of 1.75. Under volumetric strain, the formation energy increases as the strain increases. The formation energy as a function of the volumetric stress or pressure was also examined, with a minimum value of 2.00 eV at zero pressure. Using the equations of state method, we find that the formation volume of the vacancies decreases as the pressure increases, with a value of 0.6 unit-atom-volume at zero pressure. The formation enthalpy increases monotonically as the pressure increases. We predict that the avalanche pressure of alpha zirconium is −15 GPa, where vacancy formation is exothermic, causing avalanche swelling and the failure of the material.
1 Introduction
A monovacancy is a basic unit mediating mass transportation in a crystal, generally associated with self-interstitial atoms (SIAs) – another basic unit. Mechanical and kinetic processes in metals, such as dislocation climbs and self-diffusion, are associated with the evolution of vacancies. The mechanical properties of metals are greatly affected by the vacancy concentrations, which are determined by the vacancy formation energy at finite temperatures. Vacancy formation energy, the energy cost to generate a monovacancy, is a measurement of the stability of the monovacancy in the crystal. It also contributes to the self-diffusion coefficient via the monovacancy mechanism in metals.1 For example, the formation of a large vacancy loop was observed to be much easier in the presence of edge dislocations.2 Therefore, the vacancy formation energy serves as an important parameter in the understanding of the mechanical behavior of metals.On the other hand, strain greatly affects the stability of defects including vacancies. Strains have a profound influence on the properties of materials through changing the atomic structures. In materials with hexagonal-close-packed (HCP) crystal structures, the mechanical properties are anisotropic, and can be enhanced by applied strains. For example, the nucleation probability of the interstitial loops is increased on planes perpendicular to an applied strain compared to parallel ones.3–5 As a result, strain causes the transportation of atoms from planes parallel to the strain direction, to those perpendicular to the strain direction. In addition, the strain can drive the dislocation glide on planes inclined to the strain direction, as well as the dislocation climb due to the interstitial bias of the dislocations.6 More fundamentally, such anisotropic movements of dislocations are a result of the preferred absorption of point-defects under strain.4,6 A recent molecular dynamics study suggests that the anisotropic diffusion of vacancies becomes a dominant bias over the conventional dislocation bias caused by first order elastic interactions between the point defects and the sink (dislocation core, void, grain boundary, etc.).7 The influence of different atomic grain boundaries in the thermodynamic and kinetic properties of defects was also investigated.8 Furthermore, strain is widely present in micro-structures, including α zirconium (α-Zr) which has an HCP structure, due to thermal fluctuations, the presence of defects, manufacturing, or use as a structural material. However, a quantitative knowledge of the strain effect on the stability of the monovacancy in α-Zr is still lacking.
In HCP metals, two kinds of strains are important: uniaxial strain along the c direction, and volumetric strain. The volumetric strain is particularly interesting since it is closely related to irradiation swelling.9 Under uniaxial strain along the c direction, the c/a ratio of the crystal will change, in addition to the preferred absorption of point defects. There are 29 elements with HCP structures in their α phase, for which the c/a ratio ranges from 1.472 (yttrium) to 1.886 (cadmium). The c/a ratio determines the most close-packed plane in which the dislocation loop nucleation is energetically favorable. The ideal c/a ratio (1.633) corresponds to the c/a ratio in an fcc (face centered cubic) structure, which is more isotropic than an HCP structure. The most close-packed planes in an HCP structure are the prism plane {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0} for c/a < 1.633 and the basal planes (0001) for c/a > 1.633.
0} for c/a < 1.633 and the basal planes (0001) for c/a > 1.633.
The structural integrity of zirconium (Zr) and Zr alloys is of great importance due to safety issues as they are commonly used as the cladding material of fuel rods in nuclear reactors. However, due to harsh working conditions with large doses of radiation, in addition to the anisotropic HCP crystal structure, Zr has significant shape changes, even without external stress, known as radiation growth.4,7,10–18 Knowledge of the mechanism of radiation growth is critical in the design of improved alloys or the prediction of the future behavior of current alloys in service in nuclear reactors. Models based on classical inter-atomic potentials are problematic for the characterization of zirconium;19–30 part of the reason is that HCP transition metals, particularly those with c/a ratios different from the ideal value of 1.633, are poorly described by empirical inter-atomic potentials.31–33
Experimentally, it is not easy to determine the formation energy of the monovacancy precisely, because this quantity is affected by the local environment, such as the presence of impurities around the vacancy. Very pure samples are therefore required to obtain reliable results,34 and quantitative studies of the strain effects are even more challenging. Thus precise predictions rely on ab initio density functional theory (DFT) calculations.
The ultimate goal is to investigate the fundamental mechanism of the radiation growth in α-Zr, which is closely related to the stabilities of both the monovacancy and the SIAs. The stabilities of the SIAs were reported in our previous work, in which we concluded that the basal octahedral (BO) configuration is the most stable configuration,35 as confirmed by other first-principles calculations.36,37 A further study on the axial ratio (c/a) dependence of the stability of SIAs in HCP structures shows that the axial ratio dominates the relative stability of SIAs over volumetric strains.38 Below the ideal value of c/a = 1.633, the basal octahedral configuration is the most stable. Above the ideal value, the off-plane SIAs are more stable than the in-plane ones. In addition, the pressure dependent stabilities were reported recently.39 Furthermore, the diffusion of point defects in α-Zr was also studied.40–43 This shows that the Zr-vacancy plays a dominant role in the diffusion of helium in the ZrC system.44 However, the stabilities of the Zr-vacancies under strain are still elusive.
This work aims to provide accurate and reliable information about the stability of the vacancy in Zr. Therefore we studied the vacancy formation energy under various strains, in both tension and compression, axially along the c direction, and volumetrically using DFT calculations. The paper is organized as follows. Section 2 presents the details of the DFT calculations. Section 3 presents the results and analysis, followed by discussion in Section 4 and the conclusions in Section 5.
2 Density functional theory calculations
We studied the stabilities of vacancies by examining the formation energy using DFT calculations with the super cell method.45–47 Four super cells with N = 36, 96, 180, and 288 atoms were examined, which contain 3 × 3 × 2, 4 × 4 × 3, 5 × 6 × 3, and 6 × 6 × 4 primitive unit cells, respectively.Our DFT calculations were carried out using the Vienna Ab initio Simulation Package (VASP),48,49 which is based on Kohn–Sham Density Functional Theory (KS-DFT),50 with the generalized gradient approximation developed by Perdew, Burke and Ernzerhof (PBE) as the exchange–correlation function.51 The core electrons are replaced by the projector augmented wave (PAW) approach,52 which has twelve electrons (4s24p65s24d2) explicitly included as valence electrons.
The cutoff energy for the kinetic energy of the wave-functions was carefully selected to be 400 eV after convergence tests. A Gamma-centered k-mesh is required to sample the irreducible Brillouin zone in HCP structures to preserve the HCP symmetry. Here we used 7 × 7 × 7, 5 × 5 × 5, 3 × 3 × 3, and 3 × 3 × 3 Gamma-centered k-meshes for the four systems, respectively. The integration over eigenvalues is performed using the smearing technique with the Methfessel–Paxton function and a smearing width of 0.05 eV,53 which results in a convergence of the total energy with a fluctuation of less than 2 meV per cell.
The vacancy structures are optimized using the conjugate gradient method. The criterion to stop the relaxation of the electronic degrees of freedom is set as the total energy change being smaller than 10−5 eV. The optimized atomic geometry was achieved through minimizing the Hellmann–Feynman forces acting on each atom until the maximum forces on the ions were smaller than 0.03 eV Å−1. All the parameters selected will ensure the convergence of the formation energies with fluctuations of less than 0.05 eV per cell.
3 Results and analysis
We first examined the convergence of the total energy (Etot) of the primitive unit cell (2-atom cell) of α-Zr with respect to the kinetic energy cutoff Ecut for the wave functions. A dense k-mesh of 25 × 25 × 17 was used for high accuracy, which corresponds to 585 irreducible k points. The averaged energy per atom (Etot/atom) converges to −8.456 eV at Ecut = 400 eV.There is only one configuration for a monovacancy in α-Zr, in contrast to the various configurations of a SIA in α-Zr,35 or a monovacancy in compounds,54 or a monovacancy in vacancy clusters.55 Due to the layered structure of an HCP crystal, the vacancy is always in a basal plane.
3.1 Elastic properties
The lattice constants are obtained by relaxing the primitive unit cell with a cutoff energy of 1300 eV for wave functions and a cutoff energy of 2000 eV for augmentation charges for high accuracy. The elastic tensor is determined by performing six finite distortions (δε = 0.015) of the HCP lattice and deriving the elastic constants from the strain–stress relationship, where stresses were calculated ab initio by properly applied strains after a convergence test of δε.56 All internal relaxations were performed. The bulk modulus B was calculated using57
 | (1) |
The results for the lattice constant a, the c/a ratio, the bulk modulus B, and the elastic constants in HCP C11, C33, C44, C66 obtained from ab initio calculations are summarized and compared with previous studies and experiments in Table 1. They are in good agreement with both experiments58–61 and previous ab initio calculations.46,62–66
| a (Å) | c/a | B (GPa) | C11 (GPa) | C33 (GPa) | C44 (GPa) | C66 (GPa) | |
|---|---|---|---|---|---|---|---|
| Present | 3.238 | 1.600 | 93.6 | 142.7 | 165.3 | 28.8 | 38.8 |
| Expt58 | 3.23 | 1.593 | 97 | 155 | 173 | 36 | 44 |
| Expt59 | 3.231 | 1.593 | 96.5 | 144.0 | 166.0 | 33.0 | 35.0 |
| Expt60 | 3.231 | 1.593 | 93.3 | 143.4 | 164.8 | 32.0 | 39.0 |
| Expt61 | 3.230 | 1.594 | 97.2 | 155.4 | 173.0 | 36.3 | 41.4 |
| DFT62 | 3.23 | 1.604 | 92 | 142 | 164 | 29 | 39 |
| DFT46 | 3.23 | 1.600 | 94 | 146 | 156 | 28 | 42 |
| DFT63 | 3.232 | 1.603 | 94.1 | 139.4 | 162.7 | 25.5 | 34.0 |
| DFT64 | 3.24 | 1.598 | 93.4 | 141.1 | 166.9 | 25.8 | 36.8 |
| DFT65 | 3.236 | 1.597 | 96.0 | 146.7 | 163.3 | 26.0 | 39.1 |
| FP-LMTO66 | — | — | 100.3 | 153.1 | 171.2 | 22.4 | 44.9 |
3.2 Vacancy formation energy
In this study a vacancy is generated by removing a single atom from a system with N atom sites while keeping the system’s volume unchanged (constant volume).The formation energy is the energy cost of generating a defect configuration, which is used to quantify the stability of the vacancy configuration as compared to the ideal system. The vacancy formation energies are calculated at the rescaled constant volume condition with the super cell method as45–47
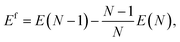 | (2) |
The vacancy formation energy is 2.06, 2.02, 2.00, and 1.97 eV for N = 36, 96, 180, and 288, respectively. Our results are in good agreement with previous calculations.67 With the increase of the system size, the formation energy decreases. However, the formation energy is indistinguishable at N ≥ 96 when the numerical errors in the DFT calculations are considered.
3.3 Strain effects
The effect of strain on the stability of the vacancy is of great importance. We studied two modes of strain: the uniaxial strain along the c direction, and a volumetric strain. In these modes, both compressive and tensile strains are examined. The vacancy formation energy under strain ε is calculated with the super cell method as,45–47
 | (3) |
 , V0 is the volume in the strain free state, V is the volume after homothetic deformation, and ε could be either uniaxial or volumetric strain. E(N − 1; V; ε) is the total energy of the system with a vacancy, which has N − 1 atoms and the volume is fixed as V first, then a strain ε is applied. The total energies are obtained after the systems are relaxed. It is worth noting that we applied artificially large strains in order to easily find the differentiable energies in the DFT calculations. We exclude the phase change in our model by using a constraint of HCP symmetry once a large strain has been applied.
, V0 is the volume in the strain free state, V is the volume after homothetic deformation, and ε could be either uniaxial or volumetric strain. E(N − 1; V; ε) is the total energy of the system with a vacancy, which has N − 1 atoms and the volume is fixed as V first, then a strain ε is applied. The total energies are obtained after the systems are relaxed. It is worth noting that we applied artificially large strains in order to easily find the differentiable energies in the DFT calculations. We exclude the phase change in our model by using a constraint of HCP symmetry once a large strain has been applied.
The formation energies under various c/a ratios calculated from three systems, with system sizes N = 36, 96, and 180, are plotted in Fig. 1. The formation energies increase with the c/a ratio at first, then decrease after a maximum. The maximum formation energy is at a c/a ratio of 1.75 (uniaxial strain of 0.09375), with a value of 2.34, 2.36, and 2.32 eV for N = 36, 96, and 180, respectively.
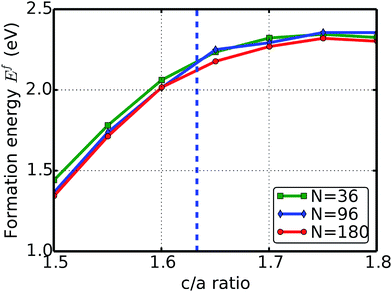 | ||
| Fig. 1 Uniaxial strain. The formation energy of a vacancy with respect to the c/a ratio (uniaxial strain). The dashed vertical line is the ideal c/a ratio (1.633). | ||
The behavior of the formation energy with respect to the c/a ratio can be understood as the following. Consider an atom with a unit-atom-volume Ω0. When the c/a ratio increases, the distance between two neighboring atomic layers enlarges. As a consequence, the Ω0 stretches along the c direction. The monovacancy formation energy is the energy gain due to the internal electronic structure rearrangement when one atom is removed. The larger Ω0 provides more space for the rearrangement of the atomic structure and the electronic charge density, which has a greater energy gain. As a result, the vacancy formation energy increases with the c/a ratio.
However, the monovacancy is always in a basal plane. When the c/a ratio becomes larger than the ideal value of 1.633, the electronic charge density decreases with the distance to the basal plane. Thus the energy gain from the rearrangement of the electronic charge density becomes saturated at a certain c/a ratio, which is 1.75 in this study.
 | ||
| Fig. 2 Volumetric strain. The variation of the formation energy of a vacancy with respect to volumetric strains in α-Zr. | ||
As the volumetric strain is applied, the total energy of the system includes the contribution from the external work which is discussed in the following subsections. However, the unit-atom-volume Ω0 swells in three-dimensions instead of stretching along the c direction only. As a result, the ratio of the increase in the vacancy formation energy to the strain is bigger than that for the uniaxial strain.
3.4 Equations of state
In our previous work, we introduced a generalized EOS method (EOS stands for “equations of state”) to study the formation energy, formation volume, and formation enthalpy of defects in an HCP crystal.39 Many analytic semi-empirical relations have been proposed to describe the EOS of various classes of solids.68–70 It is generally believed that for strains less than 30%, most EOS are similar in accuracy.71,72 Here we use the Murnaghan EOS.68 The pressure–volume relationship is expressed by the Murnaghan EOS as68
 | (4) |
 | (5) |
 | (6) |
So far the total energy of the system at any state of pressure and volume can be obtained. Now consider two systems, with and without a vacancy. We can have two sets of EOS and thus the total energies of the two systems at all states.
For each system, we calculated the total energies corresponding to seven volumes. Two systems were studied, with a vacancy and the ideal system (without a vacancy). The results of E(V) as a function of V are plotted in the upper panel of Fig. 3.
 | ||
| Fig. 3 EOS. The total energy as a function of volume (top) and the equation of state of pressure vs. volumetric strain (bottom) for the ideal system and the vacancy (179-atom) system. | ||
The fitting parameters of the vacancy and ideal systems are summarized in Table 2. Our EOS parameters agree with experiments,73,74 where B is measured as 92–102 GPa and B′ is 3.1–4.0. Using these parameters, the EOS of eqn (4) can be obtained, as plotted in the bottom panel of Fig. 3. It shows that the EOS of the ideal and vacancy systems are very similar. We only show the data within the volumetric strain range of −0.3 to 0.3 due to the limitation of the accuracy of the EOS for small strains (<30%).72 A pressure of 50 GPa corresponds to a volumetric strain of −0.26, and a pressure of −15 GPa corresponds to a volumetric strain of 0.26. We will use the pressure range of −15 GPa to 50 GPa for further study.
A pressure-induced phase transition is not directly observed from the relaxation of atoms in the static model, but through results from the comparison of the enthalpy of different possible atomic structures.65,76,77 Although real samples of Zr cannot sustain such high pressures, the theoretical study is still useful since it provides the properties of materials under high pressure, including insights into the stabilities and transition paths.
3.5 Pressure effects
Corresponding to a boundary condition of constant pressure, the formation energy at pressure P is defined as47,78
 | (7) |
For accuracy reasons, we chose the biggest super cell with a system size of N = 180 for the pressure effect study. The formation energies of a vacancy at a constant pressure Ef(P) as a function of pressure P are plotted in Fig. 4. The formation energy increases rapidly in the tensile mode but slowly in the compressive mode. When the pressure is larger than 10 GPa, the formation energy Ef(ε) increases linearly with respect to the pressure.
 | ||
| Fig. 4 Pressure effect. The formation energy of a vacancy at constant pressure Ef(P) as a function of pressure P. | ||
To have a better understanding of the effect of pressure on the formation energy of a single vacancy, we rewrote eqn (7) as:
| Ef(P) = Ed(P) + μ(P), | (8) |
| Ed(P) = E(N − 1; P) − E(N; P), | (9) |
 | (10) |
To illustrate the explicit pressure effect, we take the difference between the finite pressure and zero pressure:
| ΔEf(P) = Ef(P) − Ef(0), | (11) |
| ΔEd(P) = Ed(P) − Ed(0), | (12) |
| Δμ(P) = μ(P) − μ(0), | (13) |
We have calculated the contribution of the two components to the total formation energy in percentages as illustrated in the bottom panel of Fig. 5. It is clear that the contribution from the first component Ed decreases monotonically with an increase in pressure, from 77.41% at −15 GPa to 40.36% at 50 GPa. This behavior is opposite to that of the second component, the chemical potential energy μ, which increases monotonically with respect to pressure, from 22.59% at −15 GPa to 59.64% at 50 GPa.
The behavior of Δμ as a function of the pressure P could be understood as the following: with a larger pressure, the distance between atoms are on average reduced. As a result, the strength of the bonds are enhanced. It requires more work to introduce one more atom to the system, thus Δμ increases. For the same reason, it becomes relatively easier to remove an atom from the system, as shown by the decrease in the contribution from the change of the threshold displacement energy ΔEd as displayed in Fig. 5.
It is worth mentioning that there is a crossover of the two curves of the two components in Fig. 5 at a pressure of 26 GPa. This value of pressure is coincident with the phase change of zirconium from the ω to the β phase at a pressure of 22–33 GPa.79 This indicates that the vacancy might play a role in this phase change.
 | (14) |
Formation volumes of the vacancy at constant pressure Ωf(P) as a function of pressure P are shown in Fig. 6. The unit of Ωf(P) is Ω0 = V (N; P = 0)/N, the unit-atom-volume at zero pressure of the ideal system for convenience. In this study, Ω0 = 23.52 Å3. The formation volume decreases monotonically with respect to the pressure. The formation volume at zero pressure Ωf(0) is 0.6Ω0. This is the first time that the formation volume of α-Zr has been reported from ab initio DFT calculations. Compared with empirical many-body potentials, our results are smaller than those reported by Pasianot et al.(0.8Ω0)26 and Ackland et al.(0.74Ω0).25
| Hf(P) = Ef(P) + PΩf(P) | (15) |
The formation enthalpy of the vacancy (Hf(P)) as a function of pressure P is plotted in Fig. 7. The formation enthalpy Hf(P) monotonically increases with pressure. When the pressure is larger, the external forces have done more work on the vacancy and thus the formation enthalpy becomes larger.
The component of PΩf(P) is plotted in the bottom panel in Fig. 6. There is a maximum around P = 25 GPa due to the slow decrease of the formation volume with respect to the pressure.
It is also worth noting that the formation enthalpy is negative when the pressure is −15 GPa. This indicates that the generation of the vacancy is energetically favorable. In other words, the vacancy formation is exothermic. Such a trend will create a large amount of vacancies in an avalanche style and cause the system to fail. Because vacancies are inevitably presented in bulk α-Zr at finite temperatures, our results indicate a critical swelling pressure, namely the avalanche pressure, under which avalanche swelling occurs, leading to material failure. The region of negative formation enthalpy is the avalanche region, illustrated in Fig. 7. Our study reveals that the avalanche pressure is Pa = −15 GPa for alpha zirconium, as illustrated in Fig. 7.
4 Conclusions
In summary, we studied the stability of a monovacancy under various strains in HCP-zirconium by examining the vacancy formation energies using ab initio DFT calculations. We found that the vacancy formation energy converges with the system size at N ≥ 96 and the kinetic energy cut-off of 400 eV. There is a maximum in the curve of vacancy formation energy versus c/a ratio at c/a = 1.75, which corresponds to the uniaxial strain along the c direction with a strain value of 0.094. The formation energy at constant volume monotonically decreases with respect to the volumetric strain. However, the formation energy at constant pressure has a minimum at zero pressure, which is 2.00 eV. The formation enthalpy increases monotonically with respect to the pressure. We reported the vacancy formation volume of α-Zr as a function of pressure for the first time, which monotonically decreases with respect to the pressure, and the particular value at zero pressure is 0.6 unit-atom-volume. We predicted that at the avalanche pressure of −15 GPa, the formation enthalpy becomes negative, thus forming a vacancy is exothermic, leading to avalanche swelling and the failure of the bulk α-Zr.Acknowledgements
We would like to acknowledge the generous financial support from the Defense Threat Reduction Agency (DTRA) Grant # BRBAA08-C-2-0130, the U.S. Nuclear Regulatory Commission Faculty Development Program under contract # NRC-38-08-950, and U.S. Department of Energy (DOE) Nuclear Energy University Program (NEUP) Grant # DE-NE0000325.References
- W. Frank, U. Breier, C. Elsasser and M. Fahnle, Phys. Rev. Lett., 1996, 77, 518 CrossRef CAS PubMed.
- W. Zhou, J. Tian, J. Zheng, J. Xue and S. Peng, Sci. Rep., 2016, 6, 21034 CrossRef CAS PubMed.
- A. D. Brailsfo and R. Bullough, Philos. Mag., 1973, 27, 49 CrossRef.
- G. S. Was, Fundamentals of Radiation Materials Science: Metals and Alloys, Springer, 2007 Search PubMed.
- S. Di, Z. Yao, M. R. Daymond, X. Zu, S. Peng and F. Gao, Acta Mater., 2015, 82, 94–99 CrossRef CAS.
- L. K. Mansur, Philos. Mag. A, 1979, 39, 497 CrossRef CAS.
- C. H. Woo and X. Liu, Philos. Mag., 2007, 87, 2355–2369 CrossRef CAS.
- A. Arjhangmehr and S. A. H. Feghhi, Sci. Rep., 2016, 6, 23333 CrossRef CAS PubMed.
- P. T. Heald and M. V. Speight, Philos. Mag., 1974, 30, 869 CrossRef CAS.
- C. H. Woo, J. Nucl. Mater., 1988, 159, 237 CrossRef CAS.
- C. H. Woo, Radiat. Eff. Defects Solids, 1998, 144, 145–169 CrossRef CAS.
- R. A. Holt, J. Nucl. Mater., 1980, 90, 193 CrossRef CAS.
- R. A. Holt, J. Nucl. Mater., 1988, 159, 310 CrossRef CAS.
- V. Fidleris, J. Nucl. Mater., 1988, 159, 22 CrossRef CAS.
- R. Bullough and M. H. Wood, J. Nucl. Mater., 1980, 90, 1 CrossRef CAS.
- S. R. Macewen, R. H. Zee, R. C. Birtcher and C. Abkomeit, J. Nucl. Mater., 1984, 123, 1036–1040 CrossRef CAS.
- S. N. Buckley, Symposium on Uranium and Graphite at the Institute of Metals, Paper 6, London, 1962, p. 47 Search PubMed.
- E. J. Savino and C. E. Laciana, J. Nucl. Mater., 1980, 90, 89 CrossRef CAS.
- D. J. Bacon, J. Nucl. Mater., 1988, 159, 176 CrossRef CAS.
- D. J. Oh and R. A. Johnson, J. Mater. Res., 1988, 3, 471 CrossRef CAS.
- F. Willaime and C. Massobrio, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 11653 CrossRef CAS.
- M. Igarashi, M. Khantha and V. Vitek, Philos. Mag. B, 1991, 63, 603 CAS.
- A. G. Mikhin, Y. Osetsky and V. G. Kapinos, Philos. Mag. A, 1994, 70, 25 CrossRef CAS.
- A. S. Goldstein and H. Jonsson, Philos. Mag. B, 1995, 71, 1041 CrossRef CAS.
- G. J. Ackland, S. J. Wooding and D. J. Bacon, Philos. Mag. A, 1995, 71, 553–565 CAS.
- R. Pasianot and A. Monti, J. Nucl. Mater., 1999, 264, 198–205 CrossRef CAS.
- M. Wen, C. H. Woo and H. C. Huang, J. Comput.-Aided Mater. Des., 2000, 7, 97 CrossRef CAS.
- W. Y. Hu, B. W. Zhang, B. Y. Huang, F. Gao and D. J. Bacon, J. Phys.: Condens. Matter, 2001, 13, 1193 CrossRef CAS.
- C. H. Woo, H. Huang and W. J. Zhu, Appl. Phys. A: Mater. Sci. Process., 2003, 76, 101 CrossRef CAS.
- M. I. Mendelev and B. S. Bokstein, Philos. Mag., 2010, 90, 637 CrossRef CAS.
- L. G. Zhou and H. Huang, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 045431 CrossRef.
- L. G. Zhou and H. Huang, J. Eng. Mater. Technol., 2013, 135, 011010 CrossRef.
- R. F. Zhang, J. Wang, I. J. Beyerlein and T. C. Germann, Philos. Mag. Lett., 2011, 91, 731 CrossRef CAS.
- W. Frank, U. Breier, C. Elsasser and M. Fahnle, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 7676 CrossRef CAS.
- Q. Peng, W. Ji, H. Huang and S. De, J. Nucl. Mater., 2012, 429, 233–236 CrossRef CAS.
- G. D. Samolyuk, S. I. Golubov, Y. N. Osetsky and R. E. Stoller, Philos. Mag. Lett., 2013, 93, 93–100 CrossRef CAS.
- G. Vérité, C. Domain, C.-C. Fu, P. Gasca, A. Legris and F. Willaime, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 134108 CrossRef.
- Q. Peng, W. Ji, H. Huang and S. De, J. Nucl. Mater., 2013, 437, 293–296 CrossRef CAS.
- Q. Peng, W. Ji, J. Lian, X.-J. Chen, H. Huang, F. Gao and S. De, Sci. Rep., 2014, 4, 5735 CAS.
- G. Samolyuk, A. Barashev, S. Golubov, Y. Osetsky and R. Stoller, Acta Mater., 2014, 78, 173–180 CrossRef CAS.
- Y. Fan, S. Yip and B. Yildiz, J. Phys.: Condens. Matter, 2014, 26, 365402 CrossRef PubMed.
- J. Zheng, H. Zhang, X. Zhou, J. Liang, L. Sheng and S. Peng, Adv. Condens. Matter Phys., 2014, 929750 Search PubMed.
- O. V. Lopatina, L. A. Svyatkin, Y. M. Koroteev and I. P. Chernov, Phys. Solid State, 2015, 57, 1719–1725 CrossRef CAS.
- X. Yang, Y. Lu and P. Zhang, J. Nucl. Mater., 2015, 465, 161–166 CrossRef CAS.
- M. J. Gillan, J. Phys.: Condens. Matter, 1989, 1, 689 CrossRef CAS.
- F. Willaime, J. Nucl. Mater., 2003, 323, 205–212 CrossRef CAS.
- Z. Chen, N. Kioussis, N. Ghoniem and D. Seif, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 094102 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef CAS.
- Q. Peng, W. Ji and S. De, Nanoscale, 2013, 5, 695–703 RSC.
- Q. Peng, X. Zhang and G. Lu, Modell. Simul. Mater. Sci. Eng., 2010, 18, 055009 CrossRef.
- Y. Le Page and P. Saxe, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 104104 CrossRef.
- G. Steinle-Neumann, L. Stixrude and R. E. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 791–799 CrossRef CAS.
- E. S. Fisher and C. J. Renken, Phys. Rev., 1964, 135, A482–A494 CrossRef.
- E. A. Brandes, Smithells Metals Reference Book, Butterworth, London, 1983 Search PubMed.
- Interatomic Potentials and Crystalline Defects, Metals, Thermal and Mechanical Data, ed. S. Allard, Pergamon Press, New York, 1969, vol. 16 Search PubMed.
- S. Simmons and H. Wang, Single Crystal Elastic Constants: A Handbook, MIT Press, Cambridge, MA, 1971 Search PubMed.
- C. Domain, R. Besson and A. Legris, Acta Mater., 2002, 50, 3513 CrossRef CAS.
- H. Ikehata, N. Nagasako, T. Furuta, A. Fukumoto, K. Miwa and T. Saito, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 174113 CrossRef.
- Y.-J. Hao, L. Zhang, X.-R. Chen, Y.-H. Li and H.-L. He, J. Phys.: Condens. Matter, 2008, 20, 235230 CrossRef PubMed.
- B.-T. Wang, P. Zhang, H.-Y. Liu, W.-D. Li and P. Zhang, J. Appl. Phys., 2011, 109, 063514 CrossRef.
- E. Clouet, J. M. Sanchez and C. Sigli, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 094105 CrossRef.
- O. Le Bacq, F. Willaime and A. Pasturel, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 8508–8515 CrossRef CAS.
- F. D. Murnaghan, Proc. Natl. Acad. Sci. U. S. A., 1944, 30, 244–247 CrossRef CAS.
- P. Vinet, J. R. Smith, J. Ferrante and J. H. Rose, J. Phys. C: Solid State Phys., 1986, 19, L467 CrossRef CAS.
- P. Vinet, J. R. Smith, J. Ferrante and J. H. Rose, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 1945–1953 CrossRef CAS.
- R. Jeanloz, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 805–807 CrossRef.
- R. E. Cohen, O. Gulseren and R. J. Hemley, Am. Mineral., 2000, 85, 338–344 CrossRef CAS.
- S. N. Vaidya and G. C. Kennedy, J. Phys. Chem. Solids, 1972, 33, 1377–1389 CrossRef CAS.
- Y. Zhao, J. Zhang, C. Pantea, J. Qian, L. L. Daemen, P. A. Rigg, R. S. Hixson, G. T. Gray, Y. Yang, L. Wang, Y. Wang and T. Uchida, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 184119 CrossRef.
- C. W. Greeff, Modell. Simul. Mater. Sci. Eng., 2005, 13, 1015–1027 CrossRef CAS.
- S. Zhang, Y. Zhu, X. Zhang, S. Zhang, L. Qi and R. Liu, Comput. Mater. Sci., 2010, 50, 179–183 CrossRef CAS.
- I. Schnell and R. C. Albers, J. Phys.: Condens. Matter, 2006, 18, 1483 CrossRef CAS.
- G. Ho, M. T. Ong, K. J. Caspersen and E. A. Carter, Phys. Chem. Chem. Phys., 2007, 9, 4951–4966 RSC.
- H.-R. Wenk, P. Kaercher, W. Kanitpanyacharoen, E. Zepeda-Alarcon and Y. Wang, Phys. Rev. Lett., 2013, 111, 195701 CrossRef PubMed.
- S. Mukherjee, R. E. Cohen and O. Gulseren, J. Phys.: Condens. Matter, 2003, 15, 855–861 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2016 |



