Self-gradient mechanism, morphology and damping analysis of a thickness continuous gradient epoxy–polyurethane interpenetrating polymer network†
Xuesong Lv*a,
Zhixiong Huang*a,
Minxian Shia,
Yun Fanb and
Guanbin Gao*c
aKey Laboratory of Advanced Technology for Specially Functional Materials, Ministry of Education, Wuhan University of Technology, 122 Luoshi Road, Wuhan, Hubei Province 430070, China. E-mail: 345829300@qq.com; Tel: +86 151 7249 7866
bCollege of Foreign Languages and Literature, Luojia College, Wuhan University, Hubei 430064, PR China
cState Key Laboratory of Advanced Technology for Materials Synthesis and Processing, Wuhan University of Technology, Wuhan, Hubei Province 430070, PR China
First published on 8th November 2016
Abstract
A simple and affordable gradient-distributing interpenetrating polymer network (IPN) composite was created that takes advantage of the relatively poor compatibility and the curing rate discrepancy between epoxy (EP) and polyurethane (PU) resins. Organic element content analysis (CHNS/O) and attenuated total reflection infrared spectroscopy (ATR-FTIR) reveal that the PU content is a gradient that changes along the direction of the thickness. Morphology analysis by scanning electron microscopy (SEM) and atomic force microscopy (AFM) proves that it has a continuously changing modulus with no stratified structure. Dynamic thermomechanical analysis (DMA) and fatigue testing demonstrate that the composite has better performances than traditional homogeneous IPNs with the same compositions.
1. Introduction
Damping materials are an active area of research that has gone through several types of concepts (such as the polymer blend, copolymer and IPN).1–5 Single-component polymers were first used as vibration elimination materials. However, they have limited damping temperature regions as well as damping frequencies, and usually the glass transition regions (Tg) accompanied with their damping frequencies are not suitable for practical applications. Then, concepts such as copolymers and polymer blends arose to overcome this problem.6–9 Damping temperature range of these materials can be expanded to some degree. But owing to the relatively poor compatibility between resins, there are usually two separated damping peaks on the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ–temperature curves. What is more, the damping factors of those materials are decreased at the same time. To modify polymers with inorganic fillers or fibers (carbon black, mica powder, fiberglass, etc.) is another way to improve their damping performance. But this method can only increase the damping factor unilaterally; it usually does little to expand the damping temperature range of polymers. Subsequently, the IPN concept appeared and has proved to be the most promising technology to generate the desired damping materials. Because of the synergetic effect introduced by the forced compatibility of the individual components, IPNs have multifarious outstanding properties including damping performance when compared to other composites. So far, much attention has been paid to EP–PU IPNs for further improvement of the integrated performance. However, most modifications of PU–EP IPN composites are focused on improvements in mechanical properties; only a few papers deal with the damping properties of PU/EP IPN composites.10–12
δ–temperature curves. What is more, the damping factors of those materials are decreased at the same time. To modify polymers with inorganic fillers or fibers (carbon black, mica powder, fiberglass, etc.) is another way to improve their damping performance. But this method can only increase the damping factor unilaterally; it usually does little to expand the damping temperature range of polymers. Subsequently, the IPN concept appeared and has proved to be the most promising technology to generate the desired damping materials. Because of the synergetic effect introduced by the forced compatibility of the individual components, IPNs have multifarious outstanding properties including damping performance when compared to other composites. So far, much attention has been paid to EP–PU IPNs for further improvement of the integrated performance. However, most modifications of PU–EP IPN composites are focused on improvements in mechanical properties; only a few papers deal with the damping properties of PU/EP IPN composites.10–12
Traditional damping polymers are all limited in extensive use because the damping capacity is always an inverse relationship between Young's modulus and temperature changes.13 Thus, polymers cannot be used alone as structures but rather are attached to metal, ceramic or fiber-reinforced composite substrates to work as free-damping or constrained-layer damping structures.14–16 This is an efficient way to increase the stiffness of the structures, but this ‘sandwich structure’ will cause some surface problems, such as stress concentration, and joint failure after periods of vibration.
In 1984, the concept of functionally graded materials (FGMs) was first introduced by Japanese materials scientist M. Niino.17–19 FGMs are a class of composites with a continuous variation in material properties from one surface of the composite to another.17 The universally acknowledged problems of the classical constrained composites, such as the abrupt changing of the stress distribution at the interface as well as the low resistance to temperature shocks, can be solved with this technology. Since this new technology arrived, several methods of fabricating FGMs have been developed: powder processing, thermal spraying, chemical vapor deposition, physical vapor deposition, combustion synthesis, diffusion treatments and sedimentation.20,21 Fast and efficient technology has accelerated the manufacture of FGMs; however, the common problems of fabrication methods are equipment and material waste as well as restriction in product sizes.22 In a few cases where large-scale FGMs are manufactured, they are usually elaborate layered structures rather than truly continuous gradient materials.23,24
Recently, some methods for generating polymer gradient materials (PGMs) have also been reported.25–35 Gradient IPNs exhibit an enhanced fracture strain and more energy to break. However, their damping properties and fatigue analysis have not been reported.25–37 In addition, most PGM manufacturing processes mentioned in the literature are time-consuming and also rely heavily on devices.
Nature offers interesting examples of organisms with gradient structures.38–40 Recent studies have shown that mussel byssus can minimize interfacial stresses between adjoining stiff and soft tissue, and most important is that up to 70% of the total absorbed energy can be dissipated by the byssus.41–44
Inspired by the mussel byssus, this study explores a simple, inexpensive and repeatable way to fabricate size-controllable gradient damping materials. The driving forces in the formation of the compositional gradient IPNs are relatively poor compatibility and curing time dissimilarity between resins.
With the replacement of constrained-layer damping structures, the soft side of a PGM can be directly generated on a substrate while the rigid face is exposed outside. This type of gradient composite can be used as a replacement of the constrained-layer damping structures.45 This kind of composite will greatly reduce the interfaces in structures and the stress concentration to lengthen the service life of damping structures.
2. Experimental
2.1. Materials
Double-pack polyurethane (PU) 130T was purchased from Ausbond, of which component A (PU-a for short, 1.11 g cm−3) is the isocyanate resin and component B (PU-b, 0.98 g cm−3) is the polyalcohol. Viscosity after mixing of the two components is 1600 CPS at 25 °C. Low-viscosity epoxy LY-1564 (EP-1564, 1.06 g cm−3) was acquired from Huntsman (1200–1300 CPS at 25 °C). Curing agent 2,4,6-tris(dimethylaminomethyl)phenol (DMP-30, analytically pure) was bought from Shanghai Deyin Chemical Company. Solid phosphoric acid (chemically pure, sieved through 600 mesh) was obtained from Shanghai Yunlong Chemical Reagent Works.In order to minimize the side reactions of the resins (especially those of the isocyanate root), all the materials mentioned above were dried at 70 °C under −0.1 MPa in a vacuum oven for more than 3 hours before use.
Redistilled water was self-made and diiodomethane (analytically pure) was got from Sinopharm Chemical Reagent.
2.2. Preparation of the IPN materials
For a clear comparison of the damping properties of the IPNs, three kinds of samples were prepared: homogeneous IPN, continuous gradient IPN and graded sample.For the homogeneous sample (PU to EP equal to 4/6 by weight), 11.11 g (22.22%) PU-a, 8.89 g (17.78%) PU-b (according to the recommended dosage, PU-a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PU-b is 5/4 by weight), 1.00 g solid phosphoric acid and 30.00 g (60.00%) EP were mixed together. After stirring for several minutes, 2.4 g (8%) DMP-30 of the EP mass was dropped into the mixture. Then, the colorless liquid was put into a vacuum drying oven after a complete stir. Until there were no bubbles generated (about 4 minutes, 10 °C), the mixture was then cast into a mold and placed in a vacuum oven at a temperature of 80 °C for 12 hours. The solid phosphoric acid in this recipe was used to control the side reactions of isocyanate root.
PU-b is 5/4 by weight), 1.00 g solid phosphoric acid and 30.00 g (60.00%) EP were mixed together. After stirring for several minutes, 2.4 g (8%) DMP-30 of the EP mass was dropped into the mixture. Then, the colorless liquid was put into a vacuum drying oven after a complete stir. Until there were no bubbles generated (about 4 minutes, 10 °C), the mixture was then cast into a mold and placed in a vacuum oven at a temperature of 80 °C for 12 hours. The solid phosphoric acid in this recipe was used to control the side reactions of isocyanate root.
For the continuous gradient IPN, the recipe of the component ratios and the preparation procedure were the same as for the homogeneous one mentioned above, but the defoaming mixture was cured differently. The casting samples were horizontally placed in the vacuum oven for 24 hours (10 °C) and then postcured at 80 °C for another 12 hours.
Besides, to simulate the gradient structure, a third type of specimen (the graded sample), which consists of 6 layers of homogeneous IPN whose component ratios of PU to EP were 0/100, 6/94, 12/88, 25/75, 50/50, 100/0 separately, was made and cured at 80 °C by a layer-by-layer method. Processing procedure of each layer is also the same as for the homogeneous IPN. Thickness of each layer was 0.4 mm.
2.3. Characterization
The self-gradient phenomenon of the mixture is a comprehensive result of surface tension and adhesion of the liquid resins to the mold.Surface tensions of the cured resins are determined according to the Owens two-liquid method with redistilled water and diiodomethane.49–51 According to his theory, the contact angles between cured resins and the detecting liquids are required. They were measured using a Newjc2000X contact angle analyzer. Volume of each liquid drop was controlled to within 5 μL. Surface tensions of the cured resins can be worked out according to the following formulas:
 | (1) |
| γSV = γdSV + γpSV | (2) |
The adhesion energies Wa between the mold and the liquid resins can be calculated according to formula (3) if surface tensions of liquid resins and their contact angles with the mold are known:46,47
Wa = γLV(1 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) θ)
| (3) |
Surface tensions of the liquid resins were measured by an automatic surface tension instrument (QBZY-1, FANGRUI, China) with the BZY-A method at 10 °C (temperature of the procuring process). Contact angles between liquid resins and mold were measured as mentioned above.
Solidification curves of the resins were investigated using a Malvern Gemini 200 rheometer in oscillatory shear mode (standard parallel plate, 25 μm diameter, 1 mm gap) at 25 °C and 1 Hz. Deformation was controlled within 1% strains, which were shown to be in the linear viscoelastic limit of all the materials. EP and PU were both cured with 4% DMP-30 to simulate the real environment in the mixture.
Infrared absorption spectrum of the gradient IPN was recorded with a Nicolet 6700 using the ATR mode. For a vivid representation of the gradient structure, SEM and AFM were employed. Samples were fractured through a XJUF-5.5 cantilever beam impact tester (Chengde Jinhe) at an impact velocity of 3.5 m s−1 at 5 °C (air temperature). When a specimen was impact fractured, it would generate two fractured surfaces. One of fractured surfaces was sent for SME observation (JSM-IT300, JEOL) under an operating voltage of 20.0 kV. Another surface was used for AFM scanning. Modulus distributions of the fractured surfaces were obtained in air with Peak Force QNM mode using the J scanner of a MultiMode8 scanning probe microscope (Veeco Instruments) at room temperature after the absolute calibration method according to the literature.48–50 The fracture surface should be carefully polished by 5000 mesh abrasive papers using a PHOENIX 4000 lapping and polishing machine and vacuum drying before testing in case of the breakage of the probes.
Damping properties was recorded using a DMA/STDA 861e analyser (Mettler Toledo). Samples were standard, obtained with a hole-puncher (ϕ8.79 mm × 2.17 mm). Specimens were scanned from −50 °C to 130 °C with a heating rate of 1.5 °C min−1 in air atmosphere (shear mode, 1 Hz). The stress that the instrument produces was 2 N with an amplitude of 10 μm. In order to avoid the temperature imbalance at the beginning of the test, a temperature interval from −30 °C to 130 °C was chosen.
Fatigue testing was also carried out using the DMA/STDA 861e analyser. Samples for fatigue testing were the same as for the damping measurement. They were tested at 20 °C in air atmosphere (shear mode, 100 Hz) with an amplitude of 15 μm for 28 hours.
2.4. Reaction mechanism
Nitrogen atoms in tertiary amine (DMP-30) have larger electrophilicity than carbon atoms; they are the nucleophilic reagent. The lone pair electrons of the nitrogen atom of tertiary amine (DMP-30) will trigger the ring-opening reaction of the epoxy groups and generate the oxygen anion active center. The produced oxygen anion still has chemical activity and will trigger more ring-opening reactions.51,52 Therefore, reactions continue until all the epoxy groups open their rings and the liquid is cured finally. Curing mechanism is shown in Scheme 1.Electrons of the carbon atoms in the isocyanate root are attracted by the oxygen atoms and nitrogen atoms simultaneously. Thus carbon atoms in the isocyanate roots are electron-deficient units. Tertiary amine DMP-30 will catalyze both of the reactions between isocyanate root and hydroxyl group or hydrone. Generally speaking, DMP-30 has more of an effect on the reaction between isocyanate and the hydrone. But in this experiment, water has been eliminated beforehand. Besides, addition of the phosphoric acid will also restrict the side reactions of the isocyanate. Carbon atoms in the isocyanate roots will be attacked by the nucleophilic reagent and turn into an astatic intermediate complex.53–56 This intermediate complex has a higher reactivity and it will continue to react with the dihydric alcohol (PU-b). Because of the relatively large steric effect of benzene ring, resins will be catalyzed and cured mildly according to the stepwise polymerization and result in the polyurethane elastomers (Scheme 2).
Tertiary amine DMP-30 will accelerate the curing rates of both EP and PU components. But DMP-30 has more impact on the PU phase, which will gel and cure faster than EP to some extent. Discrepancy of curing rate between EP and PU phase is one of the driving forces for the self-gradient phenomenon of the mixture (other factors are the difference of the surface tension and low viscosity).
3. Results and discussion
If the mixture resins could cure and result in the gradient structure without any external factors, they should be incompatible or partially compatible at least.57–59 And this is the most important foundation for phase separation, gradient or layered structure. If the first element is met, then factors such as the surface/interface difference, adsorption of the mold to resins and the whole system energy should be taken into consideration. They are the parameters that determine the final gradient or layered structure. If all the factors above are satisfied (thermodynamic factors), viscosity and curing rate of the mixture are the other two factors that could influence the final structure. Only a suitable viscosity and curing rate help to form the gradient IPN structure.3.1. Thermodynamic factor analysis of the self-gradient mechanism
To have an insight into the compatibilities between epoxy and PU-a or PU-b, EP and PU-a, EP and PU-b (both of them were mixed with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio) were respectively mixed and bubbles removed. Then the mixtures were cast into tubes and sealed for 24 hours. EP-1564 is colorless and transparent while PU-b is yellowish and transparent. The color of PU-a is also faint yellow and transparent like PU-b, but it has a larger viscosity.
1 volume ratio) were respectively mixed and bubbles removed. Then the mixtures were cast into tubes and sealed for 24 hours. EP-1564 is colorless and transparent while PU-b is yellowish and transparent. The color of PU-a is also faint yellow and transparent like PU-b, but it has a larger viscosity.
Fig. 1 shows the compatibility results of the resins. The tube on the left contains epoxy and PU-b. Epoxy and PU-b have a layered structure with a distinct interface. The upper layer is PU-b and the colorless bottom layer is epoxy. This may be caused by the density disparity of resins (density of PU-b is 0.98 g cm−3 while that of epoxy is 1.06 g cm−3). From this phenomenon we can say that epoxy LY-1564 and PU-b are incompatible or only partially compatible. The mixture in the tube on the right-hand side is epoxy and PU-a. This also presents a layered structure with a fuzzy transition zone. Resin in the upper layer should be epoxy with a certain amount of PU-a dissolved in it (density of PU-a is 1.11 g cm−3). The turbidity of the resin at the bottom may be caused by two reasons. One reason is that the viscosity of the mixture (PU-a and epoxy) is too high, and more time is needed for the complete layering process; another might be the side reactions of the isocyanate root that could generate some undissolved substances.
 | ||
| Fig. 1 Compatibility of the resins. The left-hand tube contains the mixture of PU-b and epoxy while the right-hand one is filled with epoxy and PU-a. | ||
The experiment described above proved that EP-1564 and PU-a, EP-1564 and PU-b are incompatible or only partially compatible. They are thermodynamic incompatible (or partially miscible), and they have the tendency to form the layered or the gradient structures. For a further understanding of the gradient mechanism, other factors (such as the surfaces, etc.) were also studied.
Surface energies of the cured resins were determined from the contact angles according to the Owens two-liquid method. Contact angle measurements were repeated at least three times and the average values are presented in Table 1.
| H2O | CH2I2 | EP-1564 | PU | ||
|---|---|---|---|---|---|
| Contact angle | H2O | 74.39° | 110.18° | ||
| CH2I2 | 35.87° | 21.95° | |||
| γLVd (mN m−1) | 21.8 | 49.5 | |||
| γLVp (mN m−1) | 51.0 | 1.30 | |||
| γLV (mN m−1) | 72.8 | 50.8 | |||
| γSVd (mN m−1) | 37.79 | 1.91 | |||
| γSVp (mN m−1) | 5.46 | 51.22 | |||
| γSV (mN m−1) | 43.25 | 53.13 |
Liquid PU has a greater tendency to wet the mold than EP-1564 at the very beginning (Fig. 2g–i) because contact angles between PU monomers and the mold are both smaller than that of EP. Besides, the computations also proved that the surface tension of the cured PU is bigger than that of the EP (Table 1). According to surface energy theory,60 a resin that has a larger surface tension would be more likely to distribute at the bottom than that with lower surface tension. If complete phase separation occurs before curing, then it is more likely that the PU phase is mainly distributed at the bottom of the samples. The liquid EP-1564 will be extruded to the top surface.
The self-gradient phenomenon of the mixture is a comprehensive result of surface tension and adhesion (resins to the mold). Adhesion energies between mold and liquid resins can be determined according to formula (3). Surface tensions of each liquid and the corresponding contact angles (between mold and the liquids) are acquired. Surface tensions of the liquid monomer are acquired by the automatic surface tension instrument with the BZY-A method. Corresponding contact angles can be found in Fig. 2g–i.
Adhesion energy between mold and PU-a is 78.66 mN m−1, that between mold and PU-b is 63.99 mN m−1 and that between EP-1564 and mold is 68.68 mN m−1 (Table 2). This self-gradient phenomenon can be explained separately: at the beginning as the initially liquid resins and the cured products at the end.58 Adhesion energy between mold and PU-a is the largest, so it has the greatest ability to wet the mold. When the mixture is cast into the mold, the viscosity (Fig. 4) is not too high and the liquid resins have an excellent ability to flow. Monomer PU-a has more of a propensity to wet the mold and react with PU-b at the bottom of the samples under the catalysis of DMP-30 (according to the rheological measurement in Fig. 4, curing rate of PU is faster than that of EP). Surface tension of liquid EP-1564 is 46.65 mN m−1, but this decreases to 43.23 mN m−1 after curing. Surface tensions of liquid PU-a and PU-b are 42.56 mN m−1 and 34.45 mN m−1 respectively, but they increase to 51.26 mN m−1 after complete curing. PU gels and cures faster. When the surface tension of PU is larger than that of EP-1564, the PU phase will accelerate and migrate to the bottom and the EP-1564 will be extruded to the top surface according to surface tension theory.61 However, the mixture cannot separate completely due to the rising system viscosity, which will prevent macroscopic phase separation.
| Mold–** | Mold–1564 | Mold–PU-a | Mold–PU-b |
| Contact angle | 60.65° | 31.88° | 31.08° |
| Surface tension (mN m−1) | 46.64 | 42.61 | 34.41 |
| Adhesion energy (mN m−1) | 68.68 | 78.66 | 63.99 |
Presume that if the macro-phase separation of the mixture occurs before curing, then it would have two possible kinds of state, as Fig. 3 illustrates (interfaces that need to be calculated are those between air–resins, resin–resin and resins–mold). The system which has a lower system energy is more stable. If samples are in the first state (Fig. 3a) at last, then the total surface energy of this specimen will be calculated using formula (4). Correspondingly, if the second state (Fig. 3b) is more stable, then the related data will be achieved via formula (5). According to formula (6), the system which has lower system energy is more stable.
| γ1 = γEP + γPU–EP + γmold–PU | (4) |
| γ2 = γPU + γPU–EP + γmold–EP | (5) |
| γ1 − γ2 = γEP + γmold–PU − γPU − γmold–EP | (6) |
The interfacial tension γPU–EP is equal to γEP–PU. The interfacial tensions between solid layers can be worked out indirectly using the Sell–Neumann empirical equation62–64 (formula (7)) and they are listed in Table 3.
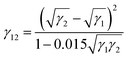 | (7) |
| 1564–PU | 1564–mold | PU–mold | |
|---|---|---|---|
| γ12 (mN m−1) | 1.713 | 0.739 | 4.515 |
The system with a lower energy will be more stable.58,59 Applying the interfacial energies into formula (4)–(6), we see that the first assumption is more stable (γ1 − γ2 < 0), and the mixture has a greater tendency to undertake phase separation progress towards the first assumption. But, in fact, complete phase separation cannot proceed due to the rising viscosity of the mixture.
3.2. Kinetic analysis of the self-gradient mechanism
Gelation of the resins will restrict the molecular diffusion and the self-gradient behavior. Under the influence of anion active agent DMP-30, the EP and PU components have different curing rates. To investigate whether the mixture has enough time to form the self-gradient structure before gelation or not, solidification curves were recorded. EP-1564, PU (with 4% of DMP-30 by weight to simulate the real environment) and their mixture (8% DMP-30) were respectively tested with a rheometer at 25 °C. A higher temperature than that of the real curing environment (10 °C) was employed to shorten the testing time.When gelation occurs, the shear elastic modulus G′ is equal to the loss modulus G′′; tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ (G′′/G′) at this time is 1.0. Fig. 4 shows that at the beginning, G′′ is bigger than G′. With time progressing, G′ grows faster than G′, and tan
δ (G′′/G′) at this time is 1.0. Fig. 4 shows that at the beginning, G′′ is bigger than G′. With time progressing, G′ grows faster than G′, and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ decreases. But within the testing time of 2 hours, the loss factors of EP and PU are both higher than 1.0. This indicates that EP, PU and their mixture are all in the liquid state. However, loss factor of PU (tan
δ decreases. But within the testing time of 2 hours, the loss factors of EP and PU are both higher than 1.0. This indicates that EP, PU and their mixture are all in the liquid state. However, loss factor of PU (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = 1.21) is lower than that of EP (tan
δ = 1.21) is lower than that of EP (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ = 4.05). This means that PU gels faster than EP. An anomaly in Fig. 4a is that G′′ decreases at the beginning and, for the time interval from 5000 s to 5800 s, a plateau can be seen. This may be caused by the gelation in tiny areas within the resin and then the “dilution effect” by the oscillation of the parallel plate. This explanation can also be used for Fig. 4b. Fig. 4c displays the curing parameters of the mixture. Within the testing time, the mixture also does not gel. On the contrary, it only takes half an hour for the mixture to cure at 80 °C in the oven. Solidification curve of the mixture looks like that of Fig. 4b except for the plateau which appears around 2500 s (about 1000 s earlier than that of PU). This is caused by the synergistic effect of the components when curing.
δ = 4.05). This means that PU gels faster than EP. An anomaly in Fig. 4a is that G′′ decreases at the beginning and, for the time interval from 5000 s to 5800 s, a plateau can be seen. This may be caused by the gelation in tiny areas within the resin and then the “dilution effect” by the oscillation of the parallel plate. This explanation can also be used for Fig. 4b. Fig. 4c displays the curing parameters of the mixture. Within the testing time, the mixture also does not gel. On the contrary, it only takes half an hour for the mixture to cure at 80 °C in the oven. Solidification curve of the mixture looks like that of Fig. 4b except for the plateau which appears around 2500 s (about 1000 s earlier than that of PU). This is caused by the synergistic effect of the components when curing.
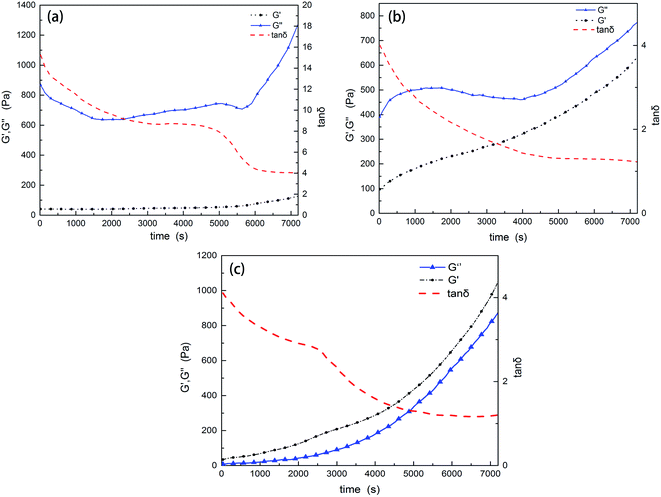 | ||
| Fig. 4 Rheological tests of the resins. (a) The curing curve of EP-1564, (b) that of PU, and (c) that of the mixture. Within the testing period of 2 hours, neither of the resins are gels. | ||
The rheological test results show that curing rates are different between the two resins and PU gels faster than EP-1564. Within the testing time of 7200 s (25 °C), the mixture is still not a gel, which allows the components to exhibit the gradient phenomenon. Another conclusion is that EP-1564 has a characteristic low viscosity. After 2 hours of reaction, G′ is still lower than 200 Pa. Considering the compositions used in this experiment (EP/PU = 6/4), the mixture does have a suitable viscosity to undergo the self-gradient process. According to surface tension theories, the resin which gelates earlier will distribute mainly in the bottom. Other resins in the mixture will be extruded to the surface.
Experiments described in Sections 3.1. and 3.2. demonstrate that the mixture does satisfy the self-gradient conditions in terms of thermodynamics and dynamics factors.
3.3. ATR-FTIR analysis
To have an insight into the gradient structure, infrared spectroscopic analysis was first employed. FTIR spectral regions of interest should be separated sufficiently far to reflect the gradient. This is because the content of the components changes continuously along the direction of thickness without any abrupt variations. Regions near h/8, h/2 and 7h/8 (from bottom to surface) along the thickness direction in the fracture surface were chosen for the ATR-FTIR analysis. Fig. 5 plots the ATR-FTIR spectra.Absorption bands at 3392 cm−1 and 1641 cm−1 are the characteristic peaks of the amine group. It is clear that there is little absorption near the surface layer (7h/8), which indicates little distribution of the PU phase. On the contrary, absorption bands in the middle and bottom regions reveal quite an amount of contents. The peak at 1738 cm−1 is the characteristic absorption of the ester group (in elastomer).65,66 The band at 1180 cm−1 corresponds to the carbon–oxygen single bond asymmetrical stretching vibration of the ester group. Only near the bottom is there enough content to show a distinct absorption versus the other locations. Bands at this point prove that the PU phase (ester group) is mainly concentrated in the bottom areas. Peaks at 1657 cm−1 and 1540 cm−1 as well as at 1240 cm−1 are ascribed to the acylamino groups.67 This proves that only a trace of the PU phase is located near the surface. Bands around 1296 cm−1, 1102 cm−1 and 1035 cm−1 offer evidence of the ether bonds. It is well known that PU contains abundant ether bonds relative to EP. The obvious absorption differences of the ether bonds also reveal gradient distribution of the PU phase along the direction of the samples. Bands around 1600 cm−1, 1580 cm−1, 1500 cm−1 and 1450 cm−1 are attributed to the vibrations of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching deformation of quinoid and benzene ring respectively.68 Because of the intense absorptions of PU, characteristic peaks of EP are hard to observe. Since the mechanism analysis above has proved that the mixture can create a gradient structure, we can safely say that the mixture resin has generated a gradient structure through the stepwise curing process.
C stretching deformation of quinoid and benzene ring respectively.68 Because of the intense absorptions of PU, characteristic peaks of EP are hard to observe. Since the mechanism analysis above has proved that the mixture can create a gradient structure, we can safely say that the mixture resin has generated a gradient structure through the stepwise curing process.
3.4. Morphology observation
Next, we used SEM and AFM to understand the gradient structure. These were performed on two fractured surfaces generated at the same point. One of the fractured surfaces was used for SEM scanning after the specimen was fractured (along the direction of the thickness) at a high speed at −30 °C. The other was used for nanoindentation. Fig. 6 shows the SEM observation of the gradient and the homogeneous IPNs. | ||
| Fig. 6 Fracture morphology of (a) the continuous gradient IPN and (b) the homogeneous one. (c)–(e) are partial enlargements (magnified by 500 times) of the positions marked in (a). | ||
Fig. 6a shows an image acquired from the gradient sample. Quite different from Fig. 6b which was scanned from the homogeneous IPN, the fractured surface of the gradient IPN can be divided into three parts. Left side (top) is brittle rupture. Bright crazing can be seen clearly especially in the partial enlarged view in Fig. 6c, which reveals the good toughening effect via a slight content of PU phase. Morphology on the right-hand side of the sample belongs to the elastic fracture. Region in the middle is the transition zone from brittle to elastic. Fig. 6b is an image of the homogeneous IPN cured at 80 °C. Fracture appearance in the homogeneous IPN is almost the same except for some phase separation and agglomeration.
Fig. 6d is a magnified image of the marked region in the middle part in Fig. 6a. Morphology in this area is quite interesting. A wrinkled and reticulate interfingering structure can be seen. Besides, a layered structure can also be found when looking from top right to bottom left. This may be caused by two reasons. Firstly, the temperature in the middle of the sample increases with the progress of the curing reaction, and this will accelerate the curing rate of epoxy. Secondly, with the PU monomer migrating towards the bottom, PU content decreases. A small quantity of PU will dissolve into EP as is shown in the right-hand tube in Fig. 1. And curing rate of PU will decrease for the relatively low content. The joint effects would result in the dissolution of EP and PU curing at the same rate, generating the wrinkled and reticulate interfingering structure.
Fig. 6e is obtained from the bottom of the gradient sample. Morphology in this region is also relatively smooth. Phase separation occurs on a very small scale. The phase domain size is about 1 μm except some agglomeration. This may be caused the relatively fast curing rate of PU at the bottom which will extrude EP out. The small quantity of EP that is trapped in PU will cure and phase separation with PU phase.
EP and PU have completely disparate mechanical properties and responses to pressure. Thus nanoindentation of AFM technology is very suitable for the detection of the gradient structure. Fig. 7 presents the AFM results of an approximate layered structure from upper left to lower right (the degree of tilt when the samples were tested).
The modulus shown in Fig. 7a is acquired near the surface of the specimen (7h/8), which is shown via purple and yellow-green colors (high modulus). The traces of red indicate little PU phase separated near the surface. The distribution histogram (Fig. 7d) shows that the modulus in this region is around 220 MPa. The small peak near 290 MPa indicates a slight phase separation near the surface of the specimen. In fact, a slight phase separation is expected to some degree because the high modulus of the pure EP on surface of the specimen will protect the soft inner parts. The modulus gradient composites can be used as replacements for the constrained damping structures when directly generated on substrates. This avoids the stress concentrations for only one interface exists in the structure. The adhesion force of this region is about 9.0 nN (Fig. 7g).
Fig. 7b is the modulus map obtained from the middle part (h/2). Different from that from Fig. 7a, the modulus there is about 100 MPa, nearly half of that shown in Fig. 7d. The adhesion force in this area is mainly around 17.5 nN (Fig. 7h), which is approximately 10 nN higher than that on the surface.
Fig. 7c comes from the bottom of the specimen (h/8). An analogous “layered” structure can be seen in this region. The thickness of the “sub-layers” is about 0.5 μm. Different from Fig. 7a, this region is mainly composed of the low-modulus PU phase. The surface of the bottom sides is so soft that even light kneading can leave a fingerprint. Only trace amounts of EP dissolve near the bottom. This phenomenon can be caused by the earlier-gelled PU phase which extruded other resins in the mixture. However, this process would have been frozen before complete phase separation. The relatively poorly dissolved components will spread layer-by-layer and finally cure to result in a gradient “sub-layered” structure. The adhesion force in this region is around 27.5 nN (Fig. 7i), which is 10 nN higher than that at the middle parts.
Based on the relationship between the composition ratios, curing time and migration rate of the resins as well as the thickness of the samples, designed structure composites can be fabricated by adjusting the experimental parameters.
3.5. Damping analysis of the IPN composites
Fig. 8a presents the damping curves of the continuous gradient IPN, the homogeneous IPN and the graded sample. The peak values of the gradient IPN are (29.95 °C, 1.59), (40.41 °C, 1.58) and (82.57 °C, 1.40) respectively; besides, some shoulder peaks can also be observed. The damping temperature range ΔT (in which the loss factor value is larger than 0.3) varies from −21.03 °C to 122.56 °C (covering a range of 143.6 °C) with an integral area TA69 of 172.56. Ideal working temperature (ΔT) of the homogeneous IPN is located from −12.31 °C to 117.32 °C (129.63 °C) with only one distinct damping peak (65.50 °C, 1.78). The corresponding TA value is 158.17. Unexpectedly, the graded IPN composite has the widest damping temperature range which ranges from −28.17 °C to 118.96 °C (147.13 °C). But it has the poorest damping factors with an integral area (TA) of 83.93. Obviously, the continuous gradient IPN composite has the best damping capacity of the three samples. And it is more suitable for use at normal temperatures. | ||
Fig. 8 (a) Loss factors (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) of the three kinds of IPN and (b) a schematic illustration of the gradient structure. δ) of the three kinds of IPN and (b) a schematic illustration of the gradient structure. | ||
Three factors are responsible for the excellent damping capacity of this continuous gradient composite.
First, interface friction is the main effect of the damping property.70 The number of interfaces is directly affected by the solubility of the components. Because of the relatively poor compatibility of the resins (more than one damping peak of the homogeneous IPN), the IPN unavoidably phase separates to produce a multiphase structure according to the thermodynamic factors.
Second, reactions of the components happen immediately when resins are mixed together. This cast specimens will gel and finally cure before complete phase separation. The relatively poor compatibility and curing rate difference result in a gradient structure. This can be considered as a composite stacked up together with infinite layers of IPN materials71,72 (as is shown in Fig. 7 and 8b). Each layer has its own glass transition temperature (Tg), which ranges from the Tg of PU to that of EP. Countless Tg values can be linked together, and the glass transition temperature changes from very low (pure PU) to normal temperature. This goes even further to the Tg of EP. Thus, the gradient composite has a broader temperature range. In fact, innumerable molecular chains run through the adjacent layers and link the layers together (Fig. 7). At a certain temperature, one layer may be at its Tg while the one close to the layer is not; hence, it has different responses during vibration compared to the neighboring layer. However, the molecular chains going across the adjacent layers will limit the deformation and increase the vibration friction.73 Indeed, friction occurs not only in each layer, but also between the close layers.
The third factor is the molecular structure. The ether bond and the carbon–carbon bond in the EP or PU phase have a lower barrier potential and more flexibility for thermal motion versus the rigid phenyl, urethane, allophanate, biuret group, etc.74 In the IPN structure, the rigid EP chains restrict the flexible bonds. Because of the forced miscibility between the phase boundaries,75 they have greater friction force during vibration than a single-component material. Besides, there are innumerable hydrogen bonds between the polar molecules. These undergo bond breaking as well as reforming during vibration. This results in more energy dissipation.76,77
The graded composite was formed by six layers of homogeneous IPNs, of which one layer is the pure PU (Tg of pure PU is −20.15 °C). Compared to any ratios of the PU/EP IPN, pure PU has the lowest glass transition temperature. So it can play a role at very low temperature. Similarly, it will also keep its function at high temperature because another layer is the pure EP (Tg of pure EP is 97.05 °C). Though the graded IPN has the broadest temperature interval, the glass transition temperatures are separated for its graded component ratio. At a certain temperature, one layer may have its best damping performance, but the others do not. This will greatly decrease the whole damping performance.
3.6. Time–temperature superposition (TTS)
Damping at low (≤0.001 Hz generally) and high frequencies (≥1000 Hz usually) is not easy to be realized due to equipment limits. However, the time–temperature equivalence principle—the equivalence of time and temperature in a viscoelastic material—is well known. That is, at low temperatures, materials will behave in the same fashion as they do at high frequencies; and at high temperatures, materials have the same response, in the same fashion, as at low frequencies. Data from extreme conditions can be easily acquired applying this theory. A master curve can be achieved according to the Williams, Landel and Ferry (WLF) equation (formula (8)) by shifting the data horizontally along the abscissa to form the desired curve:78–80
 | (8) |
According to the equation, a series of damping curves from −20 °C to 60 °C with 5 °C intervals were measured under the test conditions of 1 N and 15 μm in shear mode. The curve at 30 °C was chosen as the reference temperature (T0). Fig. 9 shows that the damping performance varies with testing frequency changes.
Because the testing process takes a long time and involves a wide range of frequencies, it is inevitable that “bad” data points might emerge by reasons of overload or errors of equipment. According to the wicket principle, both storage modulus and loss factor are unique functions of the testing frequency; so there must be a sole relationship between the storage modulus and the loss factor.81 Based on this theory, modulus and loss factor are directly labeled on the log–log coordinate (Fig. 10a). Unreasonable data or curves deviating from the others should be removed.
According to the theory mentioned above, curves at −20 °C and −15 °C (Fig. 10a) should be removed. Some other bad points marked on the graph can also be deleted. In the wicket diagram, the main curve is formed from two parts as labeled. This might be because of the non-uniform structure of this composite. Taking advantage of the wicket-filtered data, a master curve of the storage modulus or the shift factors was produced by manually shifting each curve until they superposed perfectly as shown in Fig. 10b. Below 30 °C, this gradient IPN composite is so soft that the molecular chains are frozen. The specimen will be in the glass state until the frequencies are larger than 106 Hz. The composite is mainly in the rubbery state at frequencies below 0.01 Hz.
In light of formula (8), optimum values for C1 and C2 were calculated by constructing the abscissa (T − T0) and the vertical coordinate log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αT (Fig. 10c) using Origin software. C1 is 7.462 and C2 is 80.940. The corresponding product of C1 and C2 is 603.974 (still located in the confidence interval of 400 to 900). In addition, both the adjacent r-square (0.997) and residual sum of squares (0.290) are acceptable. Thus formula (8) can be written as follows (formula (9)):
αT (Fig. 10c) using Origin software. C1 is 7.462 and C2 is 80.940. The corresponding product of C1 and C2 is 603.974 (still located in the confidence interval of 400 to 900). In addition, both the adjacent r-square (0.997) and residual sum of squares (0.290) are acceptable. Thus formula (8) can be written as follows (formula (9)):
 | (9) |
Taking 30 °C as the reference temperature T0 and applying formula (9) to the damping factors, the master curve of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ could also be obtained (Fig. 10d). Comparing Fig. 8a to 10d, tendencies of several damping peaks can still be found although they are not in strict mirror symmetry. The efficient damping frequency (at which the loss factor is larger than 0.3 (ref. 82–84)) is as wide as 109 orders of magnitude. Fig. 10d illustrates that this kind of composite matches the majority of mechanical vibrations.
δ could also be obtained (Fig. 10d). Comparing Fig. 8a to 10d, tendencies of several damping peaks can still be found although they are not in strict mirror symmetry. The efficient damping frequency (at which the loss factor is larger than 0.3 (ref. 82–84)) is as wide as 109 orders of magnitude. Fig. 10d illustrates that this kind of composite matches the majority of mechanical vibrations.
3.7. Fatigue analysis
Damping materials—the energy conversion object—are used to decrease noise and vibration under dynamic loads. Their working performance is strongly influenced by the fatigue resistance, which is usually ignored by materials scientists. Applying DMA equipment, fatigue analysis of the continuous gradient composite can be analyzed in detail. A decrease in the storage modulus can be chosen as an initial point of the fatigue failure.85Fig. 11 presents damping properties and the number of cycles. The inflection point of the shear modulus appears after 6 million cycles. The modulus decreases with a very small slope before this point. After the inflection point, the modulus begins to decrease markedly.86 This phenomenon can be explained by the growth and enrichment of the microcracks in a polymer matrix. As is known, it is inevitable that there are always flaws, such as bubbles, cavities, grooves, impurities, etc. in specimens (especially on the surface of the samples). They are the initial points where the stress concentrates. In addition, the surface stress of a specimen is always higher than interior ones under axial stress. This causes plastic slip on the surface. Under repetitive dynamic load, flaws or slips will turn into microcracks sooner or later. Due to slight changes in the structure, the modulus decreases to some degree. The temperature change also helps to explain the phenomenon of the modulus decrease.
The tips of the microcracks are the most intense areas of stress concentration. Under dynamic loads, the microcracks will grow, steer or merge into larger ones. This is the second stage of fatigue. This happens after 6 million cycles of shear. The modulus rapidly reduces with a higher slope when more microcracks or larger cracks occur. It can be supposed that with more tests, microcracks will grow into macrocracks, and the storage modulus of the samples will go through an abrupt decrease including eventual specimen fracture.85
The loss modulus has the same trend as the storage modulus, but the inflection point appears at about 3 million cycles in the fatigue test, much earlier than the storage modulus. This is because the breakage rate of the hydrogen bonds is faster than bond formation. This will decrease the dissipation of the vibration energy. At the same time, the free volume of the molecular chains increases, and the average space between them becomes larger with growth in the microcracks. Simultaneously, the internal fractions among the chains decrease to reduce the energy dissipation.
Dramatic increases in temperature appear after 9 million cycles of shear. This is the point that tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ becomes larger than the initial value. Heat is then generated faster than before and a new balance between heat production and dissipation occurs. This enhances the rate of temperature increase.87
δ becomes larger than the initial value. Heat is then generated faster than before and a new balance between heat production and dissipation occurs. This enhances the rate of temperature increase.87
4. Conclusions
A composition gradient-distributing IPN composite was manufactured simply and inexpensively in this study. ATR-FTIR indicates that the content of the PU phase gradually increases from top surface to bottom in the specimen. AFM and SEM studies reveal the IPN composite has a continuous gradient structure with no obvious phase separation or macroscopic layered structure. DMA results indicate that the continuous gradient IPN composite has an outstanding damping performance compared to the homogeneous one with the same component ratio. The time–temperature superposition demonstrates that the efficient damping frequency of the gradient composite spans more than 9 orders of magnitude. Fatigue analysis confirms that this gradient IPN can keep its excellent performances within 6 million cycles of shearing.Compared to the traditional resin–gradient IPN composites which require the use of precision injection equipment or radiation curing equipment, this paper offers a simple and inexpensive way to fabricate an EP–PU gradient IPN composite via the relatively poor compatibility and curing rate discrepancy between EP and PU by only using a vacuum oven. This method is suitable to fabricate gradient IPNs of different thickness by simply adjusting the pre-curing temperature and the pre-curing time. And this method is convenient to make various shapes of casting bodies by changing the mold. To the best of the authors' knowledge, these kinds of resin–gradient IPN composites have not been reported or used as damping materials. With a gradually changing Young's modulus, this kind of composite can be used as a replacement of the constrained damping materials by direct generation on substrates. This gradient composite will minimize the mismatch of the abrupt interfacial tension changes and reduce the adhesion failures of damping structures. The service life of these damping structures will be greatly lengthened.
Acknowledgements
The authors wish to express their gratitude to LetPub and Dr Shirley Shen from the Commonwealth Scientific and Industrial Research Organization (CSIRO) for linguistic assistance during the preparation of the manuscript. The authors are also grateful to Dr Gao Guanbin and Dr Chen Wenrui of WHUT for the AFM measurement.References
- S. Tian, F. Cui and X. Wang, Mater. Lett., 2008, 62, 3859–3861 CrossRef CAS
.
- F. Zahedi, I. A. Amraei and M. A. Fathizade, Polymer, 2016, 83, 162–171 CrossRef CAS
.
- C. L. Qin, D. Y. Zhao, X. D. Bai, X. G. Zhang, B. Zhang, Z. Jin and H. J. Niu, Mater. Chem. Phys., 2006, 97, 517–524 CrossRef CAS
.
- L. H. Sperling and J. J. Fay, Polym. Adv. Technol., 1991, 2, 49–56 CrossRef CAS
.
- M. C. Senake Perera, U. S. Ishiaku and Z. A. M. Ishak, Eur. Polym. J., 2001, 37, 167–178 CrossRef CAS
.
- K. Urayama, T. Miki, T. Takigawa and S. Kohjiya, Chem. Mater., 2004, 16, 173–178 CrossRef CAS
.
- Y. B. Wang, Z. X. Huang and L. M. Zhang, Trans. Nonferrous Met. Soc. China, 2006, 517–520 CrossRef
.
- H. Ismail and S. Suzaimah, Polym. Test., 2000, 19, 879–888 CrossRef CAS
.
- M. Hassan, K. R. Reddy, E. Haque, S. N. Faisal, S. Ghasemi, A. I. Minett and V. G. Gomes, Compos. Sci. Technol., 2014, 98, 1–8 CrossRef CAS
.
- C. Lin, S. Kuo, C. Huang and F. Chang, Polymer, 2010, 51, 883–889 CrossRef CAS
.
- M. Hassan, K. R. Reddy, E. Haque, A. I. Minett and V. G. Gomes, J. Colloid Interface Sci., 2013, 410, 43–51 CrossRef CAS PubMed
.
- J. A. Grapski and S. L. Cooper, Biomaterials, 2001, 22, 2239–2246 CrossRef CAS PubMed
.
- A. Hazarika, M. Mandal and T. K. Maji, Composites, Part B, 2014, 60, 568–576 CrossRef CAS
.
- E. E. Ungar, J. Acoust. Soc. Am., 1962, 34, 1082–1089 CrossRef
.
- D. I.G. Jones, Handbook of Viscoelastic Vibration Damping, 2001 Search PubMed
.
- M. D. Rao, J. Sound Vib., 2003, 262, 457–474 CrossRef
.
- W. Lee, S. Han and W. Park, Compos. Struct., 2015, 122, 330–342 CrossRef
.
- K. K. Pradhan and S. Chakraverty, Arch. Civ. Mech. Eng., 2015, 15, 721–734 CrossRef
.
- M. Koizumi, Composites, Part B, 1997, 28, 1–4 CrossRef
.
- A. K. Dubey, K. Kakimoto, A. Obata and T. Kasuga, RSC Adv., 2014, 4, 24601–24611 RSC
.
- J. Lambros, M. H. Santare and G. H. S. I. H. Li, Exp. Mech., 1999, 3, 184–190 CrossRef
.
- B. L. Liu, J. B. Wang, X. L. Zhong, K. Huang, B. Li, F. Wang, J. Xie and Y. C. Zhou, RSC Adv., 2014, 4, 24533–24537 RSC
.
- Y. Lin, D. Minner, V. Herring and C. Naumann, Materials, 2012, 5, 2243–2257 CrossRef CAS
.
- J. M. Silva, S. G. Caridade, N. M. Oliveira, R. L. Reis and J. F. Mano, J. Mater. Chem. B, 2015, 3, 4555–4568 RSC
.
- Z. Tang, Y. Wang, P. Podsiadlo and N. A. Kotov, Adv. Mater., 2006, 18, 3203–3224 CrossRef CAS
.
- M. M. de Villiers, D. P. Otto, S. J. Strydom and Y. M. Lvov, Adv. Drug
Delivery Rev., 2011, 63, 701–715 CrossRef CAS PubMed
.
- Y. S. Lipatov and L. V. Karbanova, J. Mater. Sci., 1995, 30, 1095–1104 CrossRef CAS
.
- S. Lin-Gibson, F. A. Landis and P. L. Drzal, Biomaterials, 2006, 27, 1711–1717 CrossRef CAS PubMed
.
- J. A. Crowe-Willoughby, K. L. Weiger, A. E. Özçam and J. Genzer, Polymer, 2010, 51, 763–773 CrossRef CAS
.
- A. M. Kloxin, J. A. Benton and K. S. Anseth, Biomaterials, 2010, 31, 1–8 CrossRef CAS PubMed
.
- N. Zaari, P. Rajagopalan, S. K. Kim, A. J. Engler and J. Y. Wong, Adv. Mater., 2004, 16, 2133–2137 CrossRef CAS
.
- T. Honma, L. Zhao, N. Asakawa and Y. Inoue, Macromol. Biosci., 2006, 6, 241–249 CrossRef CAS PubMed
.
- N. Förster, A. Pöppler, D. Stalke and P. Vana, Polymers, 2013, 5, 706–729 CrossRef
.
- E. Lai, Y. Wang, Y. Wei and G. Li, Polymers, 2016, 8, 90 CrossRef
.
- K. U. Claussen, R. Giesa and H. Schmidt, Polymer, 2014, 55, 29–38 CrossRef CAS
.
- C. Qin, W. Cai, J. Cai, D. Tang, J. Zhang and M. Qin, Mater. Chem. Phys., 2004, 85, 402–409 CrossRef CAS
.
- L. R. Carr, J. E. Krause, J. Ella-Menye and S. Jiang, Biomaterials, 2011, 32, 8456–8461 CrossRef CAS PubMed
.
- S. Thomopoulos, G. R. Williams, J. A. Gimbel, M. Favata and L. J. Soslowsky, J. Orthop. Res., 2003, 21, 413–419 CrossRef PubMed
.
- A. Miserez, T. Schneberk, C. J. Sun, F. W. Zok and J. H. Waite, Science, 2008, 319, 1816–1819 CrossRef CAS PubMed
.
- K. J. Coyne and J. H. Waite, J. Exp. Biol., 2000, 203, 1425–1431 CAS
.
- G. M. Moeser, J. Exp. Biol., 2006, 209, 1996–2003 CrossRef PubMed
.
- K. U. Claussen, T. Scheibel, H. Schmidt and R. Giesa, Macromol. Mater. Eng., 2012, 297, 938–957 CrossRef CAS
; A. Tamarin, P. Lewis and J. Askey, J. Morphol., 1976, 149, 199–221 CrossRef PubMed
.
- A. Tamarin, P. Lewis and J. Askey, J. Morphol., 1976, 149, 199–221 CrossRef CAS PubMed
.
- J. H. Waite, H. C. Lichtenegger, G. D. Stucky and P. Hansma, Biochemistry, 2004, 43, 7653–7662 CrossRef CAS PubMed
.
- D. K. Owens and R. C. Wendt, Appl. Polym. Sci., 1969, 8, 1741–1747 CrossRef
.
- D. E. Packham, Int. J. Adhes. Adhes., 2003, 23, 437–448 CrossRef CAS
.
- T. S. Meiron, A. Marmur and I. S. Saguy, J. Colloid Interface Sci., 2004, 274, 637–644 CrossRef CAS PubMed
.
- G. Gao, M. Zhang, P. Lu, G. Guo, D. Wang and T. Sun, Angew. Chem., Int. Ed., 2014, 54, 2245–2250 CrossRef PubMed
.
- M. E. Dokukin and I. Sokolov, Langmuir, 2012, 28, 16060–16071 CrossRef CAS PubMed
.
- J. Adamcik, C. Lara, I. Usov, J. S. Jeong, F. S. Ruggeri, G. Dietler, H. A. Lashuel, I. W. Hamley and R. Mezzenga, Nanoscale, 2012, 4, 4426–4429 RSC
.
- J. F. N. J. Zeno and W. Wicks, Organic Coatings Science And Technology Third Edition, Wiley-Interscience, 3rd edn, 2007 Search PubMed
.
- K. C. Cheng, W. Y. Chiu, K. H. Hsieh and C. C. M. Ma, J. Mater. Sci., 1994, 29, 721–727 CrossRef CAS
.
- M. C. Chang and S. A. Chen, J. Polym. Sci., Part A: Polym. Chem., 1987, 25, 2543–2559 CrossRef CAS
.
- J. W. Baker and D. N. Bailey, J. Chem. Soc., 1957, 8, 4652–4662 RSC
.
- J. W. Baker, M. M. Davies and J. Gaunt, J. Chem. Soc., 1949, 89, 671–681 Search PubMed
.
- J. W. Baker and J. Gaunt, J. Chem. Soc., 1949, 9, 19–24 RSC
.
- A. Mattozzi, B. Neway, M. S. Hedenqvist and U. W. Gedde, Polymer, 2005, 46, 929–938 CrossRef CAS
.
- X. Lv, Z. Huang, C. Huang, M. Shi, G. Gao and Q. Gao, Composites, Part B, 2016, 88, 139–149 CrossRef CAS
.
- D. J. Walbridge, Prog. Org. Coat., 1996, 28, 155–159 CrossRef CAS
.
- A. Mattozzi, M. S. Hedenqvist and U. W. Gedde, Polymer, 2007, 48, 5174–5180 CrossRef CAS
.
- X. Lv, Z. Huang, C. Huang, M. Shi, G. Gao and Q. Gao, Composites, Part B, 2016, 88, 139–149 CrossRef CAS
.
- A. W. Neumann, R. J. Good, C. J. Hope and M. Sejpal, J. Colloid Interface Sci., 1974, 49, 291–304 CrossRef CAS
.
- V. Fernández and M. Khayet, Front. Plant. Sci., 2015, 6, 510 Search PubMed
.
- M. Rezaei, A. F. Ismail, G. Bakeri, S. A. Hashemifard and T. Matsuura, Chem. Eng. J., 2014, 260, 875–885 CrossRef
.
- Y. R. Lee, S. C. Kim, H. Lee, H. M. Jeong, A. V. Raghu, K. R. Reddy and B. K. Kim, Macromol. Res., 2011, 19, 66–71 CrossRef CAS
.
- K. R. Reddy, B. C. Sin, K. S. Ryu, J. Kim, H. Chung and Y. Lee, Synth. Met., 2009, 159, 595–603 CrossRef CAS
.
- B. De, B. Voit and N. Karak, RSC Adv., 2014, 4, 58453–58459 RSC
.
- K. R. Reddy, K. Lee, A. I. Gopalan and A. M. Showkat, Polym. Adv. Technol., 2007, 18, 38–43 CrossRef CAS
.
- T. Trakulsujaritchok and D. J. Hourston, Eur. Polym. J., 2006, 42, 2968–2976 CrossRef CAS
.
- K. Xu, F. Zhang, X. Zhang, J. Guo, H. Wu and S. Guo, RSC Adv., 2015, 5, 4200–4209 RSC
.
- P. Y. Wang, L. R. Clements, H. Thissen, W. B. Tsai and N. H. Voelcker, Acta Biomater., 2015, 11, 58–67 CrossRef CAS PubMed
.
- D. W. F. L. H. Sperling, J. Appl. Polym. Sci., 1969, 7, 425–427 Search PubMed
.
- X. Zhao, P. Xiang, M. Tian, H. Fong, R. Jin and L. Zhang, Polymer, 2007, 48, 6056–6063 CrossRef CAS
.
- C. Peter and K. Kremer, Soft Matter, 2009, 5, 4357 RSC
.
- U. Sorathia, W. Yeager and T. Dapp, J. Sound Vib., 1990, 382–396 Search PubMed
.
- C. Wu, T. Yamagishi, Y. Nakamoto, S. Ishida, S. Kubota and K. Nitta, J. Polym. Sci., Part B: Polym. Phys., 2000, 1496–1503 CrossRef CAS
.
- S. H. Kim, J. P. K. Tan, F. Nederberg, K. Fukushima, J. Colson, C. Yang, A. Nelson, Y. Yang and J. L. Hedrick, Biomaterials, 2010, 31, 8063–8071 CrossRef CAS PubMed
.
- C. Briody, B. Duignan, S. Jerrams and S. Ronan, Polym. Test., 2012, 31, 1019–1025 CrossRef CAS
.
- W. Yu, R. Li and C. Zhou, Polymer, 2011, 52, 2693–2700 CrossRef CAS
.
- J. A. Pathak, R. H. Colby, S. Y. Kamath, S. K. Kumar and R. Stadler, Macromolecules, 1998, 31, 8988–8997 CrossRef CAS
.
- E. H. P. N. B. Mayoral, RSC Adv., 2015, 52395–52409 RSC
.
- T. Wang, S. Chen, Q. Wang and X. Pei, Mater. Des., 2010, 31, 3810–3815 CrossRef CAS
.
- S. Chen, Q. Wang and T. Wang, Mater. Des., 2012, 38, 47–52 CrossRef
.
- C. Qin, W. Cai, J. Cai, D. Tang, J. Zhang and M. Qin, Mater. Chem. Phys., 2004, 85, 402–409 CrossRef CAS
.
- B. Dong, C. Liu and Y. Wu, Polym. Test., 2014, 38, 40–45 CrossRef CAS
.
- M. S. Loo, J. B. Le Cam, A. Andriyana, E. Robin and J. F. Coulon, Polym. Degrad. Stab., 2016, 124, 15–25 CrossRef CAS
.
- A. Bernasconi, F. Cosmi and D. Taylor, Polym. Test., 2014, 40, 149–155 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra13093c |
| This journal is © The Royal Society of Chemistry 2016 |









