Effect of alloying elements on the ideal strength and charge redistribution of γ′-Ni3Al: a first-principles study of tensile deformation
Abstract
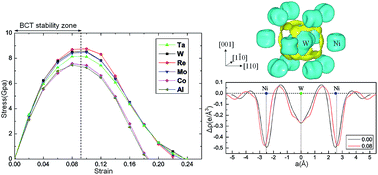
The ideal strength, which is the minimum stress required to yield a perfect crystal, is fundamental for understanding the mechanical properties of real materials. Using density functional theory, the effect of the alloying elements Ta, W, Re, Mo, and Co on the ideal tensile strength (σIT) of γ′-Ni3Al along three characteristic directions was investigated. By examining the crystal mechanical stability in terms of Born criteria at every single strain during the tensile tests, the σIT values of L12-Ni3Al along the [001], [110] and [111] directions are determined to be 12.93 GPa, 7.20 GPa and 25.55 GPa, respectively. The effect of alloying elements on σIT shows obvious directionality because of directional interactions between impurities and host atoms. Doping with Ta, W, Re, Mo, and Co increases σIT in the [110] direction by 13%, 18%, 21%, 17%, and 5%, respectively. Furthermore, the electronic mechanism underlying the strengthening effect of alloying elements is determined by analyzing the d-orbital partial density of states and charge redistribution.

 Please wait while we load your content...
Please wait while we load your content...