Structural transitions and electronic properties of sodium superoxide at high pressures

Abstract

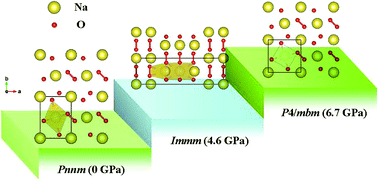
Sodium superoxide (NaO₂) has attracted considerable attention as the main discharge product in Na–air batteries due to its specific energy, which exceeds that of the Li-ion battery. Pressure has become an irreplaceable tool to improve or alter the physical properties of a given material. By utilizing first-principles swarm structure-searching predictions, herein, we for the first time investigate the structures and electronic properties of NaO₂ in the pressure range of 0–20 GPa. It is found that the orthorhombic Pnnm structure at ambient pressure transforms to another orthorhombic Immm structure at approximately 4.6 GPa, and subsequently to the tetragonal P4/mbm structure at 6.7 GPa. The pressure-induced structural transitions are mainly derived from the denser polyhedral packing and higher coordination number. It is interesting to find that the superoxide group (O₂⁻) is maintained over the entire pressure range considered. Analysis of the electronic band structure and density of states shows that the structures found exhibit intriguing half-metallic magnetism. This study enables an opportunity to understand the structures and electronic properties of NaO₂ at high pressures.

---

1 Introduction

The typical oxide formed by sodium is sodium oxide, Na₂O, which has Na and O in the +1 and −2 oxidation states, respectively. Sodium and oxygen can also combine to form sodium peroxide (Na₂O₂) and sodium superoxide (NaO₂) in which the peroxide group (O₂²⁻) or superoxide group (O₂⁻) acts as anions. Each oxygen atom in O₂²⁻ has an oxidation state of −1, whereas each oxygen atom in O₂⁻ possesses a −0.5 oxidation state. Thus, O₂⁻ has a single unpaired electron and exhibits paramagnetism. Because NaO₂ is the main discharge product in Na–air batteries, much attention has been paid to investigate its structures and physical properties.^1,2 Moreover, the performance improvement of Na–air batteries strongly depends on the knowledge and understanding of its discharge products.

Templeton and Daubel first reported NaO₂ in 1950.³ NaO₂ has an FeS₂-type structure (space group Pnnm, 2 formula unit per cell) at ambient pressure and a temperature of 4.2 K.⁴ With an increase in temperature, the Pnnm structure transforms to the Pa3 and Fm3̄m structures at 230 and 300 K, respectively. Fm3̄m-structured NaO₂ is a disordered pyrite structure.⁵ The main differences among the three phases are the ordering of the superoxide ion O₂⁻. NaO₂ has a rich variety of applications.⁶ For example, NaO₂ can be utilized as a component of oxygen regeneration devices.^5,7–9 NaO₂ is an intriguing magnetic material because its magnetism originates from the superoxide group, O₂⁻, which is in sharp contrast to the magnetic origin of compounds containing transition metals or rare-earth elements.⁸ Further studies show that the relative alignment of O₂⁻ has a great effect on its magnetic properties.^10,11 Unlike Li–air batteries, where Li₂O₂ is the main discharge product, NaO₂ has been identified as the dominant discharge product in Na–air batteries because of the faster one electron transfers compared with those in Na₂O₂.^12–15

Pressure has multiple effects, such as overcoming reaction barriers,¹⁶ altering atomic orbital energy levels,¹⁷ inducing structural transitions,¹⁸ and modifying electronic properties.¹⁹ As a consequence, pressure has become an irreplaceable tool to discover new materials with exciting physical and chemical properties.^20–22 In this study, we for the first time explore the structural evolution of NaO₂ up to 20 GPa using an unbiased structure searching method in combination with first-principles calculations. The other two stable structures for NaO₂ with Immm and P4/mbm symmetries emerge at 4.6 and 6.7 GPa, respectively. In contrast to the ground structure at 0 GPa, the higher coordination number and denser polyhedral packing make the two structures energetically favorable at high pressures. The paramagnetism originating from O₂⁻ is maintained under the considered pressure ranges. Our results are also important for understanding the behaviors of O₂⁻ under high pressure.

2 Computational details

The underlying ab initio structural relaxations and electronic calculations were performed using density functional theory within the Perdew–Burke–Ernzerhof (PBE) of parameterization of the generalized gradient approximation (GGA),^23,24 as implemented in the Vienna Ab Initio Simulation Package (VASP) code.^25–27 The all-electron projector-augmented-wave (PAW)²⁸ pseudopotentials were adopted with 3s¹ and 2s²2p⁴ treated as valence electrons for the Na and O atoms, respectively. PAW potentials have shown good predictive capability in battery materials.^29–34 Monkhorst–Pack sampling³⁵ with the grid spacing of 2π × 0.015 Å⁻¹ and cutoff energy of 600 eV were used to ensure that the total enthalpy calculations are converged to less than 1 meV per atom. The force converge was set to 1 × 10⁻³ eV Å⁻¹ and the energy convergence threshold was 1 × 10⁻⁶ eV per cell. Phonon calculations, as implemented in the Phonopy code,³⁶ were performed to determine the dynamical stability of the predicted structures.

Our structural prediction was performed as implemented in the CALYPSO (Crystal structure Analysis by Particle Swarm Optimization) structure prediction code, which is based on the global minimization of free energy surfaces and merges ab initio total-energy calculations.^37,38 This method is unbiased by any prior known structural information, and only depends only on chemical composition. Its success has been demonstrated with various systems, ranging from elements to binary and ternary compounds.^39–46 In this study, structure prediction with simulation cell sizes of 1–4 formula units was performed at pressures of 0, 5, 10, 15 and 20 GPa. The structure search for NaO₂ at different pressures converged (evidenced by no structure with a lower enthalpy emerging) after 1000–1200 structures were investigated (i.e. in about 20–30 generations). Detailed description of the structural predictions is given in the ESI.† Crystal structures and polyhedrons were visualized using the VESTA tool.⁴⁷

3 Results and discussion

Structure searches were performed for the NaO₂ stoichiometry with up to 4 formula units (f.u.) per simulation cell at 0, 5, 10, 15 and 20 GPa. The ambient pressure phase (space group Pnnm, 2 f.u. per cell) was successfully reproduced in our structural search.

Moreover, the lattice parameters of the Pnnm structure were optimized to be a = 4.17, b = 5.61, and c = 3.43 Å, which are in good agreement with the experimental values of 4.26, 5.54, and 3.44 Å, respectively.⁴ These results indicate the validity of both the structural prediction method and pseudopotentials adopted. The enthalpy difference (ΔH) of the predicted structures and experimental Pa3̄ phase relative to the ambient pressure phase (space group Pnnm, 2 f.u. per cell) was calculated as a function of pressure and is shown in Fig. 1. In general, a lower enthalpy corresponds to a more stable phase. As observed from Fig. 1, the ground state Pnnm structure of NaO₂ at ambient pressure transforms to the Immm structure (3 f.u. per cell) at 4.6 GPa. Then, NaO₂ undergoes another transition from the Immm to P4/mbm structure at 6.7 GPa. Moreover, the two predicted phases are dynamically stable because of no imaginary phonon modes in the Brillion zone (Fig. S1†). According to the partial phonon density of states analysis, the vibration of the Na–O bond mainly contributes to the low frequency regimes, whereas the high frequency regimes mainly originate from the O–O stretching mode, which is also similar to those observed in LiO₂,⁴⁸ thus indicating that the superoxide group (O₂⁻) in our considered two phases is maintained over the whole considered pressure range. Complex structural changes can be observed upon these phase transitions, as will be discussed below.

Fig. 1 The relative enthalpy per formula unit with respect to the Pnnm structure as a function of pressure within the PBE calculation at T = 0 K for the considered NaO₂ structures.

At a certain pressure, P, the structure with the lowest enthalpy (H = U + PV) is the most stable, where U and V are the energy and volume per formula unit, respectively.⁴⁹ In general, the structure with a smaller volume is favorable at high pressure because it can effectively decrease the enthalpy value. The corresponding volume variations as a function of pressure of the considered structures were calculated and shown in Fig. 2. It can be observed that the volume collapses with 11.11% (5.99%) from the Pnnm to Immm (from Immm to P4/mbm) phase transition, which suggests that the characters of the two considered phase transitions are similar to the cases of Li₂O₂ and CaO₂.^50,51 At the same time, it amounts to a lowering of the PV term with the enthalpy of ∼0.06 eV per formula unit for Immm relative to the Pnnm structure, which can be found in Fig. 3a. In addition, the U of Immm is larger than that of Pnnm, as shown in Fig. 3b. Combining the U and PV terms, Immm phase becomes energetically favorable from 4.6 to 6.7 GPa (Fig. 1). Similar results can be found for the Immm to P4/mbm phase transition (Fig. 3(c) and (d)). Therefore, the volume decrease induced by pressure is the main factor in determining the phase transition process.

Fig. 2 Calculated volume variations as a function of pressure for the Pnnm, Immm and P4/mbm phases.

Fig. 3 (a) PV and (b) U curves for Immm relative to the Pnnm structures of NaO₂; (c) PV and (d) U curves for P4/mbm relative to the Immm structures.

As mentioned above, NaO₂ adopts the Pnnm structure. Then, it transforms to Immm, followed by the P4/mbm phase. The crystal structures of these phases and Na-centered polyhedrons are shown in Fig. 4. The calculated lattice parameters and atomic positions for the three considered structures at their phase transition pressures are listed in Table S1.† For the orthorhombic structure Pnnm, each Na atom forms a six-fold coordination with O atoms, having two different Na–O distances of 2.39 Å and 2.38 Å, respectively. The O–O distance is calculated to be 1.35 Å, which is in good agreement with the experimental value (1.33 Å).⁴ The Immm structure contains two inequivalent Na occupying the 2a (0.0, 0.0, 0.0) and 4f (0.832, 0.0, 0.5) positions. The former Na atom is surrounded by the six nearest O atoms, whereas the latter Na atom is coordinated by eight O atoms. The increased coordinated number results in a reduction of the volume, which makes the Immm structure energetically stable. Moreover, the average Na–O distance of 2.36 Å in the Immm structure at 4.6 GPa is slightly shorter than that in the Pnnm structure. It is noted that the distance between the two nearest oxygen atoms is 1.34 Å, indicating that the superoxide group is maintained upon this pressure-induced phase transition. In P4/mbm, the Na–O coordination number is 8, which is the highest coordination number among all the known NaO₂ phases. The Na–O distance is further reduced to 2.34 Å. The O–O bond length is 1.33 Å, which is slightly shorter than the distances (1.35 Å and 1.34 Å) at ambient pressure and 4.6 GPa, respectively. Based on the abovementioned analysis, the Na–O and O–O distances in the three considered phases become shorter and shorter with an increase in the pressure. As a consequence, their phase transition mechanisms can be attributed to the higher coordination number and denser polyhedral packing.

Fig. 4 Crystal structures: (a) NaO₂ with Pnnm symmetry at ambient pressure, (b) NaO₂ with Immm symmetry at 4.6 GPa, and (c) NaO₂ with P4/mbm symmetry at 6.7 GPa.

To test the anisotropic stress response, the normalized lattice constants of the three considered structures were calculated and illustrated in Fig. 5, where a₀, b₀ and c₀ are the lattice constants of the Pnnm structure at T = 0 K and P = 0 GPa. It is found that the incompressibility along the a- and b-directions is much larger than that of the c-direction. As shown in the structural analysis, the effect of pressure on the Na–O bond length is larger that of the O–O bond. In other words, the Na–O bond is more easily compressed than the O–O bond. For the considered phases, the Na–O and O–O bonds are mainly along the a- and b-directions, whereas the c-direction only contains Na–O bonds.

Fig. 5 Calculated normalized lattice constants for the Pnnm, Immm and P4/mbm structures of NaO₂ as a function of pressure.

The three considered phases are ferromagnetic. Their magnetic moments are 1.0, 0.9 and 1.0 μB per f.u. at 0.0, 4.6 and 6.7 GPa, respectively. These results imply that the effect of pressure on magnetic moment is very small. This is also in agreement with the slight bond length variation of the superoxide group under pressure. To further understand the electronic properties, we calculated the spin-polarized band structures and density of states (DOS) of the Pnnm, Immm and P4/mbm phases at the phase-transition pressures (Fig. 6). For clarity, the spin-up and spin-down energy band structures and corresponding DOS are shown, respectively. The three considered phases exhibit half metallic magnetism, wherein the spin-down is metallic and the spin-up is semiconductor. The spin-up PBE band gaps of Pnnm, Immm and P4/mbm are 5.05, 4.24 and 5.19 eV at 0.0, 4.6 and 6.7 GPa, respectively, indicating that the Immm phase has the smallest band gap. Analysis of the DOS shows that the magnetism and conducting states arise from the superoxide O₂⁻ groups. The same mechanism for superoxide-induced magnetism and metallicity was also observed in Li₃O₄ compound.⁵² For the considered phases, there is a dominant O p character around the Fermi energy, which is mainly response for the electronic properties.

Fig. 6 Spin-polarized electronic band structures and spin-dependent total and density of states (DOS) of NaO₂ within the Pnnm phase at 0 GPa (a), the Immm phase at 4.6 GPa (b), and the P4/mbm phase at 6.7 GPa (c). The red and black lines represent the spin-up and spin-down energy bands, respectively. The black dashed lines denote the Fermi level.

4 Conclusions

Unbiased structure searching combined with density functional total energy calculations was used to explore the structural phase transitions and electronic properties of NaO₂ up to 20 GPa. Two novel high-pressure phases, Immm and P4/mbm, were identified at ∼4.6 and 6.7 GPa, respectively. During the phase transition, the Na atom coordination number gradually increases. Moreover, the Na–O and O–O bond lengths decrease with an increase in pressure. As a consequence, the phase transition mechanism mainly originates from the higher coordination number and denser polyhedral packing. Analysis of the electronic band structure reveals that the two high-pressure NaO₂ phases are half-metallic and magnetic. It is hoped that this study will stimulate further experimental studies on NaO₂ at high pressure.

Acknowledgements

The authors gratefully acknowledge financial support from the National Natural Science Foundation of China (21573037 and 21173035) and the Natural Science Foundation of Jilin Province (20150101042JC) and the Postdoctoral Science Foundation of China under grant 2013M541283.

Notes and references

1. O. Arcelus, C. Li, T. Rojo and J. Carrasco, J. Phys. Chem. Lett., 2015, 6, 2027–2031.
2. S. Kang, Y. Mo, S. P. Ong and G. Ceder, Nano Lett., 2014, 14, 1016–1020.
3. D. H. Templeton and C. H. Dauben, J. Am. Chem. Soc., 1950, 72, 2251–2254.
4. G. F. Carter and D. H. Templeton, J. Am. Chem. Soc., 1953, 75, 5247–5249.
5. S. Yang and D. J. Siegel, Chem. Mater., 2015, 27, 3852–3860.
6. P. Singh and N. K. Gaur, Phys. Lett. A, 2007, 371, 349–353.
7. B. Lee, D.-H. Seo, H.-D. Lim, I. Park, K.-Y. Park, J. Kim and K. Kang, Chem. Mater., 2014, 26, 1048–1055.
8. P. Hartmann, D. Grübl, H. Sommer, J. Janek, W. G. Bessler and P. Adelhelm, J. Phys. Chem. C, 2014, 118, 1461–1471.
9. I. V. Solovyev, Z. V. Pchelkina and V. V. Mazurenko, CrystEngComm, 2014, 16, 522–531.
10. M. Kim and B. I. Min, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 121106.
11. T. Knaflič, M. Klanjšek, A. Sans, P. Adler, M. Jansen, C. Felser and D. Arčon, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 174419.
12. P. Hartmann, C. L. Bender, J. Sann, A. K. Durr, M. Jansen, J. Janek and P. Adelhelm, Phys. Chem. Chem. Phys., 2013, 15, 11661–11672.
13. C. L. Bender, P. Hartmann, M. Vračar, P. Adelhelm and J. Janek, Adv. Energy Mater., 2014, 4, 1301863.
14. B. D. McCloskey, J. M. Garcia and A. C. Luntz, J. Phys. Chem. Lett., 2014, 5, 1230–1235.
15. P. Hartmann, C. L. Bender, M. Vračar, A. K. Dürr, A. Garsuch, J. Janek and P. Adelhelm, Nat. Mater., 2013, 12, 228–232.
16. E. Zurek, R. Hoffmann, N. W. Ashcroft, A. R. Oganov and A. O. Lyakhov, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 17640–17643.
17. M. S. Miao, Nat. Chem., 2013, 5, 846–852.
18. Y. Ma, M. Eremets, A. R. Oganov, Y. Xie, I. Trojan, S. Medvedev, A. O. Lyakhov, M. Valle and V. Prakapenka, Nature, 2009, 458, 182–185.
19. R. S. McWilliams, D. K. Spaulding, J. H. Eggert, P. M. Celliers, D. G. Hicks, R. F. Smith, G. W. Collins and R. Jeanloz, Science, 2012, 338, 1330–1333.
20. P. F. McMillan, Chem. Soc. Rev., 2006, 35, 855–857.
21. Y. Wang and Y. Ma, J. Chem. Phys., 2014, 140, 040901.
22. Y. Wang, L. Jian, Z. Li, L. Shaohua, Y. Ketao, L. Quan, W. Hui, Z. Lijun and M. Yanming, J. Phys.: Condens. Matter, 2015, 27, 203203.
23. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
24. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
25. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
26. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
27. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
28. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
29. Y. Mo, S. P. Ong and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 205446.
30. D.-H. Seo, H. Gwon, S.-W. Kim, J. Kim and K. Kang, Chem. Mater., 2010, 22, 518–523.
31. D.-H. Seo, H. Kim, H. Kim, W. A. Goddard and K. Kang, Energy Environ. Sci., 2011, 4, 4938–4941.
32. D.-H. Seo, H. Kim, I. Park, J. Hong and K. Kang, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 220106.
33. D.-H. Seo, Y.-U. Park, S.-W. Kim, I. Park, R. A. Shakoor and K. Kang, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 205127.
34. G. Yang, S. Shi, J. Yang and Y. Ma, J. Mater. Chem. A, 2015, 3, 8865.
35. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
36. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
37. Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116.
38. Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070.
39. L. Zhu, H. Liu, C. J. Pickard, G. Zou and Y. Ma, Nat. Chem., 2014, 6, 644–648.
40. J. Lv, Y. Wang, L. Zhu and Y. Ma, Phys. Rev. Lett., 2011, 106, 015503.
41. L. Zhu, H. Wang, Y. Wang, J. Lv, Y. Ma, Q. Cui, Y. Ma and G. Zou, Phys. Rev. Lett., 2011, 106, 145501.
42. D. Nishio-Hamane, M. Zhang, T. Yagi and Y. Ma, Am. Mineral., 2012, 97, 568–572.
43. Y. Wang, H. Liu, J. Lv, L. Zhu, H. Wang and Y. Ma, Nat. Commun., 2011, 2, 563.
44. Q. Li, D. Zhou, W. Zheng, Y. Ma and C. Chen, Phys. Rev. Lett., 2013, 110, 136403.
45. M. Zhang, H. Liu, Q. Li, B. Gao, Y. Wang, H. Li, C. Chen and Y. Ma, Phys. Rev. Lett., 2015, 114, 015502.
46. G. Yang, Y. Wang, F. Peng, A. Bergara and Y. Ma, J. Am. Chem. Soc., 2016, 138, 4046–4052.
47. K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658.
48. K. C. Lau, L. A. Curtiss and J. Greeley, J. Phys. Chem. C, 2011, 115, 23625–23633.
49. C. J. Pickard and R. J. Needs, Nat. Mater., 2008, 7, 775–779.
50. N. Deng, W. Wang, G. Yang and Y. Qiu, RSC Adv., 2015, 5, 104337–104342.
51. J. R. Nelson, R. J. Needs and C. J. Pickard, Phys. Chem. Chem. Phys., 2015, 17, 6889–6895.
52. G. Yang, Y. Wang and Y. Ma, J. Phys. Chem. Lett., 2014, 5, 2516–2521.

---

Footnote

† Electronic supplementary information (ESI) available: Computational detail of the structural prediction; the phonon dispersion curve for the considered for NaO₂; the calculated structural information of the predicted NaO₂ structures at selected pressures. See DOI: 10.1039/c6ra12328g

---