Synthesis and multistate characterization of bis-flavylium dications – symmetric resorcinol- and phloroglucinol-type derivatives as stochastic systems

Abstract

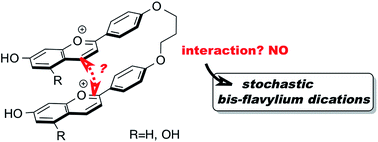
Two symmetric bis-flavylium dications were readily synthesized and further evaluated for their multistate profile. Both systems were shown to be fully stochastic and behave like a single compound suggesting that the two flavylium moieties do not communicate via the bridge linking them. Global pK_a values of ca. 4 regarding the acid–base reaction between flavylium cation and quinoidal base were calculated using a stopped flow technique. It was further demonstrated that the equilibrium between AH⁺–AH⁺ and indistinguishable flavylium-quinoidal base isomers AH⁺–A (A–AH⁺) can be calculated by subtracting 0.3 pH units from the observed acid–base constant. On the other hand, the equilibrium between both flavylium-quinoidal base isomers and the bis-quinoidal base A–A is obtained by adding 0.3 pH units. Moreover, both systems do not have a cis–trans isomerization barrier and the rate constants of interconversion between flavylium cation and quinoidal base as a function of pH are fitted with a mono-exponential and follow a bell-shaped curve. The systems proved also to be photochromic and from the fitting of the bell-shaped curve, flash photolysis measurements and quantum yields, it is possible to calculate all rate and equilibrium constants and construct a global energy-level diagram. It was also proved that the rate constant to form both isomers AH⁺–C_t from the bis-flavylium upon a pH jump from 1 to less acidic solutions is twice that of the observed value and the formation of the bis-trans-chalcone from both isomers AH⁺–C_t is equal to the observed rate constant. An energy-level diagram of all the multistate species was constructed from the equilibrium constants.

---

Introduction

Flavylium (2-phenyl-1-benzopyrylium) derivatives constitute an important family of natural pigments, which comprise (i) anthocyanins, the molecules responsible for most of the red and blue colors of flowers and fruits,^1,2 and (ii) 3-deoxyanthocyanidins, the colorants appearing in ferns and mosses as well as hybrids of sorghum and purple corn.³ Besides the above mentioned natural pigments, a myriad of non-natural flavylium derivatives have been synthesized, some of them exhibiting relevant photochromic properties with practical applications as models for optical memories, molecular logic gates and even to mimic elementary properties of neurons.⁴

From a structural viewpoint, flavylium compounds are generally defined by the respective flavylium cation, which is nevertheless only one of the species of a reversible sequence of chemical reactions that are interconnected by external stimuli, such as pH, light and removing or adding electrons (redox).^4b,5 As illustrative example, if one considers oenin which is the major flavylium-based pigment of European grapevine species (i.e., Vitis vinifera), this natural anthocyanin is known to be pushed into a well-established multiequilibria network involving five distinct structural forms: the red-colored flavylium cation (AH⁺) and its colored quinoidal conjugate base (A), the colorless hemiketal species (B) as well as its colorless (or pale-yellow) ring-opened counterparts (C_c and C_t) (Scheme 1).⁶

Scheme 1 Flavylium multistate systems – the case of oenin as illustrative example.

In order to characterize such a flavylium multistate system,^7,8 it is necessary to perform direct pH jumps defined as the addition of base to equilibrated solutions of the flavylium cation (generally for pH < 1), thus triggering the sequence of reactions shown in Scheme 1. Also it is required to carry out reverse pH jumps, obtained by addition of acid to equilibrated solutions at higher pH values.

Thus, after a direct pH jump, the flavylium cation (AH⁺) yields the quinoidal base (A) upon proton transfer in competition with hydration in position 2 to give the hemiketal (B) (Fig. 1, eqn (a) vs. eqn (b)). The proton transfer is by far the faster reaction of the multistate and by consequence A is formed before B. One important breakthrough in this system was reported in the late seventies by Brouillard and Dubois, who showed that A does not hydrate in acidic medium.⁹ Consequently, the evolution of the system takes place through the hemiketal while the quinoidal base is a kinetic product that is in fast equilibrium and disappears simultaneously with AH⁺. On the other hand, hemiketal B could further open ring C and form cis-chalcone (C_c) (Fig. 1, eqn (c)), itself in slow isomerization equilibrium with the trans-chalcone (C_t) (Fig. 1, eqn (d)). At higher pH values, ionized species are formed by deprotonation of the remaining hydroxyl groups (not shown in Scheme 1). Altogether, the system can be simplified considering a single acid base equilibrium involving the species AH⁺ (acid) and CB (basic) where CB = A + B + C_c + C_t (Fig. 1, eqn (e)).

Fig. 1 Flavylium multistate systems – summary of the implicated chemical equilibria and the corresponding kinetic/thermodynamic constants.

Regarding the kinetic processes after a direct pH jump, the respective mathematical expressions are different according to the existence or the lack of the cis–trans isomerization barrier. In the first case, as in anthocyanins, three distinct steps are observed (Fig. 2, Math.(a–c)). The first corresponds to the proton transfer, the second to the hydration, considering that tautomerization is faster (which is the general case except for very acidic pH values in reverse pH jumps experiments), and the third is the isomerization reaction.

Fig. 2 Flavylium multistate systems – mathematical expressions of the key kinetic constants.

Regarding the reverse pH jumps carried out from equilibrated or pseudo-equilibrated solutions, eqn (d) and (e) presented in Fig. 2 account for the respective kinetics. The first one is observed when the final pH of the reverse pH jump is less acidic, while the second corresponds to the case of regime change: the hydration becomes faster than tautomerization at very high proton concentrations, and the last reaction is the controlling step of the kinetic process. In the absence of the cis–trans isomerization barrier only one kinetic process (besides proton transfer) is observed as reported (Fig. 2, Math.(f)). Representation of this rate constant (i.e., k_obs) as a function of pH is a bell shaped curve, where the left branch is controlled by the isomerization reaction while the right branch by the hydration.¹⁰

To go further, shifting from flavylium monocations to more sophisticated dicationic flavylium-based skeletons appears attractive, because enabling the network of chemical reactions to be influenced/extended by the presence of the second cationic moiety. Although the synthesis of such sophisticated flavylium-based systems, as flavylium-benzopyrylium¹¹ skeleton A and bis-flavylium skeletons B–E,¹² has been reported in the literature (Fig. 3), their multistate characterization remains surprisingly very few documented. To our knowledge, the bis-flavylium C where two flavylium units are linked via a redox-responsive methyl viologen bridge constitutes the only system whose multistate behavior has been evaluated to date.^12b Remarkably, the performed studies have revealed that the system is not fully stochastic, especially regarding the isomerization event (Fig. 1, eqn (d)).

Fig. 3 Selected examples of flavylium-based dications A–D and tetracation E (^asee ref. 11; ^bsee ref. 12a; ^csee ref. 12b; ^dsee ref. 12c; ^esee ref. 12d).

In this context and due to our interest in flavylium chemistry^4b,11,12a,13 as well as their potent applications,^4b,c,8,14 we report herein on the synthesis and the full multistate characterization of two symmetric bis-flavylium dications, the resorcinol- and phloroglucinol-type salts 1 and 2 respectively (Fig. 4).

Fig. 4 Symmetric bis-flavylium dications 1 and 2 studied in the present work.

Results and discussion

Synthesis

The synthesis of bis-flavylium 1 and 2 was achieved in line with a procedure recently reported by us (Scheme 2).^12a The procedure consists of a four-step sequence taking advantage of the acid-mediated condensation between bis-arylethynylketone 5 and resorcinol/phloroglucinol as last and key step. The required condensation partner 5 was first prepared in three steps starting from commercially available and cheap materials, namely 4-hydroxybenzaldehyde and 1,3-dibromopropane. After coupling two equivalents of 4-hydroxybenzaldehyde with one equivalent of the dibrominated alkylating agent, the resulting bis-benzaldehyde 3 was then efficiently converted to 5 via a nucleophilic addition–oxidation sequence, involving bis-propargynol derivative 4 as intermediate and employing ethynyl magnesium bromide as nucleophilic reagent and 2-iodoxybenzoic acid (IBX) as oxidant. With 5 in hand, the key condensation step proved highly efficient with either resorcinol or phloroglucinol, furnishing the desired bis-flavylium 1 and 2 in almost quantitative yields. The easy-to-perform ‘click’ feature of the bis-condensation deserves here to be reminded, notably because the dications 1/2 are isolated in pure forms due to a very simple work-up (i.e. a filtration/washing sequence). Also worth noting is that both dications were obtained with an excellent efficiency over the four steps, i.e. 75% and 74% overall yields for 1 and 2 respectively.

Scheme 2 Synthesis of bis-flavylium dications 1/2. Reagents and conditions: (a) 1,3-dibromopropane (1.0 equiv.), 4-hydroxybenzaldehyde (2.4 equiv.), K₂CO₃ (3.0 equiv.), DMF, 100 °C, 12 h; (b) 3 (1.0 equiv.), HCCMgBr (2.6 equiv.), THF, 0 °C to rt, 3 h; (c) 4 (1.0 equiv.), IBX (4.0 equiv.), EtOAc, 80 °C, 12 h; (d) 5 (1.0 equiv.), resorcinol (R=H) or phloroglucinol (R=OH) (2.0 equiv.), aqueous HPF₆ (xs), AcOH, rt, 48 h.

Characterization of multistate systems

With these two symmetric bis-flavylium 1/2 in hand, we next investigated their multistate behavior, taking into account as starting hypothesis that two equal flavylium multistates are present in the molecules.

Physicochemistry. The pH dependent spectral variations of compounds 1 and 2 monitored by stopped flow 10 ms after a direct pH jump are shown in Fig. 5A and B respectively. Inspection of these figures indicates that these spectral changes are compatible with a single acid–base equilibrium involving the cationic flavylium forms and its quinoidal bases. The isosbestic points show that flavylium forms disappear by increasing pH to give exclusively the quinoidal bases (in this time scale). In the cases of both compounds 1/2, fitting was achieved by a single acid–base equilibrium with pK_a(1) = 3.9 and pK_a(2) = 4.0.

Fig. 5 UV/Vis spectral variations occurring upon a direct pH jump from stock solutions of compounds 1/2 at pH 1 (2.5 × 10⁻⁵ M/9.3 × 10⁻⁶ M) to higher pH values. Spectra recorded immediately after the pH jump in the case of 1 (A) and in the case of 2 (B). Spectra recorded at the thermodynamic equilibrium in the case of 1 (C) and in the case of 2 (D). Insets: fittings (–) of the absorbance values (●/○) at the specified wavelengths.

The global acid–base equilibrium can be accounted for by equation eqn (f) and the network of chemical reactions depicted in Scheme 3.^8,15 The pK_a1 is defined as the acid–base equilibrium between the diprotonated form (A₂H₂²⁺) and the sum of the monoprotonated species (A₂H⁺), while pK_a2 between the monoprotonated species (A₂H⁺) and the neutral form (A₂). As mentioned above, both systems behave as a single acid–base equilibrium corresponding (i) in the case of 1, to the stochastic constant pK_am(1) = 3.9 and by consequence pK_a1(1) = 3.6 and pK_a2(1) = 4.2, and (ii) in the case of 2, to pK_am(2) = 4.0, pK_a1(2) = 3.7 and pK_a2(2) = 4.3. Accordingly, these data then allowed us to determine the mole fraction distribution of the respective species as shown in Fig. 6A and B.

Scheme 3 Deprotonation sequences of the bis-flavylium.¹³

Fig. 6 Mole fraction distribution of the diprotonated–monoprotonated and neutral species of the equilibrium (i) between flavylium cation and quinoidal base in the case of 1 (A) and in the case of 2 (B), and (ii) at the thermodynamic equilibrium in the case of 1 (C) and in the case of 2 (D).

Remarkably, both bis-flavylium systems also behave as a single acid–base at the thermodynamic equilibrium, thus involving flavylium cation and trans-chalcone (Fig. 1, eqn (e)). Fig. 5C and D indeed show the pH-dependent absorption of solutions of 1/2 after equilibration for ca. 24 h, revealing an extremely small pK′_a value for 1 (i.e. 0.7 and 3.3 for 1 and 2 respectively). These values compare with pK′_a = 1.5 for the model compound 4′-methoxy-7-hydroxyflavylium in the same conditions (i.e. 50% water/ethanol, v/v, room temperature, see Fig. S1 in ESI†). Considering again the systems as stochastic, the corresponding global equilibrium can be accounted for by equation eqn (g) depicted in Fig. 7. The same reasoning as above then leads to pK′_a1(1) = 0.4 and pK′_a2(1) = 1.0 (compares with pK′_a1(1) = 3.0 and pK′_a2(1) = 3.6 for (2)), further confirming the unusual higher acidity of the bis-flavylium 1.

Fig. 7 Deprotonation sequence of the bis-flavylium at the thermodynamic equilibrium.

Having proved that the systems 1/2 are both stochastic, the following discussion considers that similarly to the acid–base reaction all micro-rate and equilibrium constants are the same and the systems can be treated as a single one multistate flavylium.

From the spectra of Fig. 5A and B to the spectra at the equilibrium (Fig. 5C and D), the systems evolve according to a single mono-exponential decay as clearly shown in the insets of Fig. 8A and B. First, regarding the bis-flavylium 1, representation of a series of direct pH jumps as a function of pH was fitted with equation Math.(f) (Fig. 2) for the parameters pK_a(1) = 3.9, k_hk_tk_i = 1.15 × 10⁻⁶ M⁻¹ s⁻¹, k_−i = 10⁻⁵ s⁻¹ and k_tk_i/k_−h = 1.9 × 10⁻⁴ M⁻¹ s⁻¹ (Fig. 8C). At extremely low pH values, a term equal to k^H_cat[H⁺] should be added, k^H_cat = 7.6 × 10⁻⁴ M⁻¹ s⁻¹ should be added to account for a catalytic step recently observed as a general behavior of flavylium networks most probably due to the catalytic effect by proton on the chalcones isomerization. Of note the so-obtained representation of the k_obs rate constant as a function of pH is a typical bell-shaped curve, where the left branch is controlled by the isomerization reaction while the right branch by the hydration.

Fig. 8 (A) Spectral variations of 1 after a direct pH jump from pH 1 to pH 5 – inset: fitting of the absorbance at 493 nm gives k_obs = 3.5 × 10⁻⁴ s⁻¹ at pH 3.9. (B) Spectral variations of 2 after a direct pH jump from pH 1 to pH 6.3 – inset: fitting of the absorbance at 493 nm gives k_obs = 7.0 × 10⁻⁵ s⁻¹ at pH 4. (C) Regarding 1, representation of a series of direct pH jumps (●) and reverse pH jumps (○) from pH 7. (D) Same as (C) but in the case of 2. (E) Decay of the flavylium cation 1 and trans-chalcone formation after a direct pH jump as in the inset of (A) (red lines) – kinetics of the bis-flavylium disappearance to give the intermediate with a unique flavylium and the final bis-trans-chalcone.

In a similar way, fitting of the experimental data in Fig. 8B with eqn (g) (Fig. 7) was achieved for the parameters pK_a(2) = 4.0, k_hk_tk_i = 1.3 × 10⁻⁸ M⁻¹ s⁻¹, k_−i = 2.2 × 10⁻⁵ s⁻¹, k_tk_i/k_−h = 8.5 × 10⁻⁷ M⁻¹ s⁻¹ and k^H_cat = 1.5 × 10⁻³ M⁻¹ s⁻¹ (Fig. 8D).

As shown in Appendix 2 given in ESI† and taking into account that the systems are stochastic, the rate constants for the formation of the species AH⁺–AH⁺, AH⁺–C_t (C_t–AH⁺) and C_t–C_t can be calculated. Interestingly enough, it can be proved that the intermediate species bearing one flavylium cation and a trans-chalcone at each terminal is formed with a rate constant two times higher than the rate constant of the observed global process and disappears with the same rate constant of the global process.

Photochemistry. In the case of flavylium multistates lacking the cis–trans isomerization barrier the number of relations between rate and equilibrium constants of the system is not enough to carry out their full characterization. However, in some cases it is possible to use other stimuli rather than pH jumps to shift the multistate from the equilibrium and follow the relaxation processes and in this way get more information regarding the multistate. This is the case of the trans–cis photo-induced C_t=C_c isomerization.

As shown in Fig. 9A and B, the present bis-flavylium compounds 1/2 both exhibit photochromism because upon irradiation, the absorption band of the flavylium cation increases at the expenses of its trans-chalcone form. Furthermore, representation of the quantum yields as a function of pH are presented in Fig. 9C and D.

Fig. 9 (A) Spectral variations upon irradiation of 1 at pH = 3.8, λ_irr = 376 nm. (B) Spectral variations upon irradiation of 2 at pH = 4.2, λ_irr = 370 nm. (C) Quantum yields of the photochemical reaction involving 1 as a function of pH – fitting was achieved with Math.(k) and (l) (Fig. 11). (D) Same as (C) but in the case of 2.

For clarity reasons, the following discussion will focus more particularly on bis-flavylium 1. The flash photolysis of 1 was carried at different pH values, and is shown for equilibrated solutions at pH 2 (Fig. 10A). After the flash, there is a bleaching at 376 nm, a wavelength where trans-chalcone C_t shows its absorption maximum. The bleaching occurs because the species formed is cis-chalcone C_c that has a low molar absorption coefficient at this wavelength. The absorption at 376 nm is partially recovered in ca. 0.2 s at this pH value, indicating that part of cis-chalcone C_c gives back trans-chalcone C_t. At the same time and with identical lifetime, the flavylium cation is formed and as a result, the fraction of non-recovered trans-chalcone C_t corresponds to the fraction of so-formed flavylium cation. Representation of the rate constants of the flash photolysis experiments is shown in Fig. 10A and, as observed for other flavylium multistates, the rates of the flash photolysis follow two regimes. At higher pH values, since the hydration is much slower than tautomerization, the equilibrium between hemiketal and cis-chalcone is attained and Math.(g) (Fig. 11) could be used. At lower pH values occurs the change of regime and hydration is much faster than tautomerization. Thus, all the hemiketal that is formed upon ring closure gives immediately flavylium cation and Math.(h) (Fig. 11) should be used for fitting.

Fig. 10 (A) Traces of the flash photolysis of 1 at pH 2. (B) Rate constants of the flash photolysis as a function of pH – fitting was achieved with Math.(g) and Math.(h) (Fig. 11).

Fig. 11 Flavylium multistate systems – mathematical expressions of the kinetic constants and quantum yields related to the photoinduced isomerization process.

The pH-dependent quantum yields reported in Fig. 9C provide also significant kinetic information that can be used to calculate the rate and equilibrium constants of the system. When the hydration is the rate-determining step, the equilibrium between B and C_c is established and the forward and backward reactions are respectively given by Math.(i) (Fig. 11) and eqn (e) (Fig. 1), assuming that the tautomerization equilibrium is achieved.¹⁶ Further neglecting the contribution of k_−i as well as k_h[H⁺]/([H⁺] + K_a),¹⁷ the pH-dependence of the quantum yield is thus given by Math.(k) (Fig. 11).

On the other hand, when the rate determining step is the tautomerization reaction as observed in Fig. 10, the pH dependence of the quantum yield then follows Math.(l) (Fig. 11).

A global fitting was finally carried out using eqn (e) and Math.(f–l), the resulting values of the parameters being summarized in Table 1.

Table 1 Fitting parameters used to fit kinetic data^a

	KhKtki (M^−1 s^−1)	Ktki/k−h (M^−1 s^−1)	k−h/(1 + Kt) (M^−1 s^−1)	kiKt/(1 + Kt) (s^−1)	ki + k−t (s^−1)
a With k^H = 5 M^−1 s^−1 and k^OH = 2 × 10^9 M^−1 s^−1 for 1 and k^H = 200 M^−1 s^−1 and k^OH = 5 × 10^9 M^−1 s^−1 for 2.
1	1.5 × 10^−6	1.9 × 10^−4	1.4 × 10^3	0.26	0.36
2	1.3 × 10^−8	8.5 × 10^−7	6.0 × 10^4	0.03	0.7

---

Full characterization. From the parameters reported in Table 1, it is possible to calculate all the rate and equilibrium constants of the system 1 and thus fully characterize its multistate behavior. The data of the rate and equilibrium and kinetic constants of 1 are presented respectively in Tables 2 and 3. In parallel, the full multistate characterization of bis-flavylium 2 was performed using the same overall reasoning and the calculated values are also given in Tables 2 and 3.

Table 2 Equilibrium constants of bis-flavylium 1 and 2

	pKa/pK′a	Kh (M^−1)	Kt	Ki
a The large error between this theoretical value and the experimental (i.e. 0.7) is most probably due to the uncertainty in measuring the pH values at these extremely acidic solutions.
1	3.9/0.9^a	1.2 × 10^−6	2.7	3.55 × 10^4
2	4.0/3.3	3.5 × 10^−7	0.05	2.70 × 10^4

---

Table 3 Rate constants of bis-flavylium 1 and 2

	kh (s^−1)	k−h (M^−1 s^−1)	kt/k−t (s^−1)	ki/k−i (s^−1)
1	6.05 × 10^−3	5.1 × 10^3	0.04/0.015	0.355/10^−5
2	1.5 × 10^−2	4.3 × 10^4	0.005/0.1	0.6/2.2 × 10^−5

---

Finally, the data reported in Tables 1 and 2 allow the construction of an energy-level diagram which is very useful to account for the details of the multistate, in particular to illustrate the photochemistry (Scheme 4). In the particular case of 1, the quantum yield at pH 3.9 is higher than at pH 5 because the forward reaction from C_c to AH⁺/A is more efficient in the former. The thermal back reaction to restore the equilibrium is much slower in both cases. The species B and C_c are not easily accessible from the thermodynamic point of view. Moreover, at pH 5, the thermal back reactions are slower than at pH 3.9. This is due to the fact that at pH 5 there is more A in comparison with AH⁺. As mentioned in the introduction, A is thus a kinetic product that retards the system to get the equilibrium. A similar situation is observed in the case of 2 (see Fig. S3 in ESI†).

Scheme 4 Energy-level diagram of bis-flavylium 1. Illustration of the pathways upon irradiation of the trans-chalcone (A) at pH 5, where the rate-determining step is the hydration. (B) The same at pH 3.9 where the hydration is faster.

Conclusions

Symmetric bis-flavylium systems pose some interesting theoretical questions regarding the influence of the bridge on the chemical behavior of each terminal flavylium multistate. The present system proved to be stochastic in the sense that there is no measurable interaction between both flavylium multistates. The kinetics and thermodynamics of the bis-flavylium is identical to a single flavylium multistate lacking of a cis–trans isomerization barrier. However, using the statistics, it is possible to calculate the distribution of the species at the molecular level. The pK_a1 for removing one proton from the bis-flavylium is 0.3 units lower than the observed pK_a (macroscopic) while the pK_a2 for removing the second proton is 0.3 units greater. The same is calculated for the equilibrium involving flavylium cation and trans-chalcone (macroscopic pK′_a). Information of the kinetics at the molecular level can also be achieved mathematically. While the kinetic process after a direct pH jump is a single exponential (k_obs), the rate at the molecular level to give one trans-chalcone is twice k_obs and the rate to give the second trans-chalcone from the remaining flavylium cation is the same as k_obs.

Experimental section

Synthesis

General. All starting materials were commercial and were used as received. Anhydrous solvents were freshly distilled before use or were obtained from the M. Braun Solvent Purification System (MB-SPS-800). The reactions were monitored by thin-layer chromatography carried out on silica plates (silica gel 60 F₂₅₄, Merck) using UV-light for visualization. Column chromatographies were performed on silica gel 60 (0.040–0.063 mm, Merck) using mixtures of ethyl acetate and cyclohexane as eluents. Evaporation of solvents were conducted under reduced pressure at temperatures less than 30 °C unless otherwise noted. Melting points (mp) were measured with a Stuart SMP30 apparatus in open capillary tubes and are uncorrected. IR spectra were recorded with a Perkin-Elmer FTIR 1600 spectrometer (KBr disc) and values are reported in cm⁻¹. ¹H and ¹³C NMR spectra were recorded on (i) a Bruker Avance 300 spectrometer at 300 and 75 MHz, respectively, and on (ii) a Bruker Avance 500 spectrometer at 500 and 125 MHz, respectively. Chemical shifts δ and coupling constants J are given in ppm and Hz, respectively. Chemical shifts δ are reported relative to residual solvent as an internal standard (acetonitrile-d₃: 1.94 ppm for ¹H and 1.32/118.3 ppm for ¹³C; DMSO-d₆: 2.50 ppm for ¹H and 39.5 ppm for ¹³C). ¹H multiplicities are designated by the following abbreviations: s = singlet, d = doublet, t = triplet, m = multiplet, quint. = quintuplet, b = broad. Carbon multiplicities were determined by DEPT135. UV-Visible spectra were measured with a 8452A Hewlett-Packard spectrophotometer in the solvents indicated. Maximum absorption wavelengths λ_max and molar extinction coefficients ε are given in nm and mol⁻¹ dm³ cm⁻¹. Electrospray (ESI) and Desorption Chemical Ionization (DCI) low/high-resolution mass spectra were obtained from the ‘Service Commun de Spectroscopie de Masse’ of the Plateforme Technique, Institut de Chimie de Toulouse.

Procedure for the synthesis of 4,4′-(propane-1,3-diylbis(oxy))dibenzaldehyde 3. To a solution of 1,3-dibromopropane (2.02 g, 10.0 mmol, 1.0 equiv.) in DMF (30 mL) were added 4-hydroxybenzaldehyde (2.93 g, 24.0 mmol, 2.4 equiv.) and K₂CO₃ (4.15 g, 30.0 mmol, 3.0 equiv.). The mixture was heated at 100 °C and stirred overnight (i.e., 12 h). After cooling the reaction mixture to room temperature, H₂O (30 mL) was added to the mixture in order to precipitate the reaction product. The mixture was filtered and the crude product was purified by column chromatography (cyclohexane/EtOAc – 9 : 1 to 7 : 3) to give 3 in pure form as a white solid (2.55 g, 90%). R_f = 0.4 (cyclohexane/EtOAc, 7 : 3, v/v); mp: 131–132 °C; IR (KBr): ν_max = 1690 cm⁻¹; ¹H NMR (300 MHz, DMSO-d₆): δ = 9.87 (s, 2H), 7.88–7.85 (m, 4H), 7.17–7.14 (m, 4H), 4.27 (t, J = 6.6 Hz, 4H), 2.25 (quint., J = 6.3 Hz, 2H) ppm; ¹³C NMR (75 MHz, DMSO-d₆): δ = 191.3, 163.4, 131.8, 129.7, 114.9, 64.7, 28.3 ppm; MS (DCI⁺) m/z (%): 285 (25) [M − H⁺], 302 (100) [M − NH₄⁺].

Procedure for the synthesis of 1,1′-(4,4′-(propane-1,3-diylbis(oxy))bis(4,1-phenylene))diprop-2-yn-1-ol 4. To a solution of 3 (1.02 g, 3.6 mmol, 1.0 equiv.) in THF (10 mL) was added a solution of commercial ethynylmagnesium bromide (0.5 M in THF, 19 mL, 9.4 mmol, 2.6 equiv.) at 0 °C. After addition of the Grignard reagent, the mixture was let warm and stirred at rt until the complete consumption of 3 (TLC). A saturated solution of NH₄Cl was then added to the reaction mixture and the THF was evaporated under vacuum. The aqueous phase was extracted three times with EtOAc and the organic layers were washed with H₂O and brine and then dried over Na₂SO₄. After evaporation of the solvent, the resulting crude product was purified by column chromatography (cyclohexane/EtOAc – 4 : 1) to give 4 as a pale yellow solid (1.08 g, 89%). R_f = 0.2 (cyclohexane/EtOAc, 7 : 3, v/v); mp: 109–110 °C; IR (KBr): ν_max = 3330, 3300, 2110 cm⁻¹; ¹H NMR (300 MHz, DMSO-d₆): δ = 7.37–7.34 (m, 4H), 6.95–6.92 (m, 4H), 5.90 (d, J = 6.0 Hz, 2H), 5.27 (dd, J = 6.0, 2.4 Hz, 2H), 4.12 (t, J = 6.0 Hz, 4H), 2.16 (quint., J = 6.3 Hz, 2H) ppm; ¹³C NMR (75 MHz, DMSO-d₆): δ = 158.0, 134.1, 127.8, 114.1, 85.8, 75.6, 64.3, 62.0, 28.6 ppm; MS (DCI⁺) m/z (%): 319 (100) [M − OH⁺], 336 (15) [M⁺], 354 (30) [M − NH₄⁺].

Procedure for the synthesis of 1,1′-(4,4′-(propane-1,3-diylbis(oxy))bis(4,1-phenylene))diprop-2-yn-1-one 5. To a solution of 4 (2.5 mmol, 1.0 equiv.) in EtOAc (15 mL) was added freshly prepared IBX¹⁸ (2.8 g, 10 mmol, 4.0 equiv.) in one portion. The mixture was heated at 80 °C and stirred overnight (i.e., 12 h). After cooling the reaction mixture to room temperature, the mixture was filtered and EtOAc was evaporated under vacuum. The resulting crude product was purified by column chromatography (cyclohexane/EtOAc, 4 : 1 to 1 : 1) to give 5 as a yellow solid (815 mg, 98%). R_f = 0.3 (cyclohexane/EtOAc, 7 : 3, v/v); mp: 145–146 °C; IR (KBr): ν_max = 3230, 2090, 1635 cm⁻¹; ¹H NMR (300 MHz, DMSO-d₆): δ = 8.05–8.02 (m, 4H), 7.16–7.13 (m, 4H), 5.00 (s, 2H), 4.28 (t, J = 6.3 Hz, 4H), 2.25 (quint., J = 6.3 Hz, 2H) ppm; ¹³C NMR (75 MHz, DMSO-d₆): δ = 175.3, 163.7, 131.7, 129.0, 114.8, 84.5, 80.3, 64.8, 28.2 ppm; MS (DCI⁺) m/z (%): 333 (20) [M − H⁺], 350 (100) [M − NH₄⁺].

General procedure for the synthesis of bis-flavylium compounds 1/2. To a solution of resorcinol or phloroglucinol (1.0 mmol, 2.0 equiv.) and bis(arylethynylketone) 5 (0.5 mmol, 1.0 equiv.) in AcOH (2 mL) was added aqueous HPF₆ (0.5 mL, 60% in water). The solution, becoming immediately dark red, was stirred at rt for 48 hours. The resulting mixture was then plunged into Et₂O (20 mL) where the bis-flavylium dihexafluorophosphate precipitated. The solid was recovered by filtration, washed with Et₂O and finally dried under vacuum to give the expected dicationic species 1 and 2, from resorcinol and phloroglucinol respectively.
Bis(1′-((7-hydroxy)benzopyrylium)phenoxy)propane dihexafluorophosphate 1. Yellow solid (386 mg, 96%). IR (KBr): ν_max = 3380, 1635, 855 cm⁻¹; ¹H NMR (500 MHz, 1% TFA-d₁ in CD₃CN): δ = 9.01 (d, J = 8.5 Hz, 2H), 8.42–8.41 (m, 4H), 8.19 (d, J = 8.8 Hz, 2H), 8.12 (d, J = 8.8 Hz, 2H), 7.52 (d, J = 1.9 Hz, 2H), 7.44 (dd, J = 8.8, 2.2 Hz, 2H), 7.29–7.27 (m, 4H), 4.43 (t, J = 6.2 Hz, 4H), 2.38 (quint., J = 6.1 Hz, 2H); ¹³C NMR (125 MHz, 1% TFA-d₁ in CD₃CN): δ = 173.4, 168.8, 167.4, 159.9, 155.0, 133.8, 133.4, 122.4, 122.3, 120.3, 117.5, 114.1, 103.9, 66.6, 29.4 ppm; UV/Vis (CH₃CN/10% 1 N HCl): λ_max (ε) = 466 (39 000), 262 nm (16 000 mol⁻¹ dm³ cm⁻¹); MS (ESI⁺) m/z (%): 259 (100) [M²⁺].
Bis(1′-((5,7-dihydroxy)benzopyrylium)phenoxy)propane dihexafluorophosphate 2. Yellow solid (400 mg, 95%). IR (KBr): ν_max = 3410, 1640, 855 cm⁻¹; ¹H NMR (500 MHz, 1% TFA-d₁ in CD₃CN): δ = 9.04 (d, J = 8.8 Hz, 2H), 8.32–8.27 (m, 4H), 7.94 (d, J = 8.8 Hz, 2H), 7.21–7.18 (m, 4H), 6.96 (d, J = 2.2 Hz, 2H), 6.72 (d, J = 2.2 Hz, 2H), 4.38 (t, J = 6.2 Hz, 4H), 2.35 (quint., J = 6.2 Hz, 2H); ¹³C NMR (125 MHz, 1% TFA-d₁ in CD₃CN): δ = 160.1, 159.6, 150.4, 133.2, 122.6, 117.7, 114.2, 111.5, 104.0, 96.9, 66.7, 29.9 ppm; UV/Vis (CH₃CN/10% 1 N HCl): λ_max (ε) = 476 (21 000), 416 (sh), 326 (6000), 278 nm (15 000 mol⁻¹ dm³ cm⁻¹); MS (ESI⁺) m/z (%): 275 (100) [M²⁺].

Characterization of full multistates systems

General. Stock solutions of 1 and 2 were prepared in H₂O : EtOH 1 : 1 (v : v) with HCl 0.1 M. The pH jumps were carried out by addition of base (direct) or acid (reverse) to equilibrated solutions of 1 or 2. The pH of the solutions was adjusted by addition of HCl, NaOH, or Theorell and Stenhagen's universal buffer and pH was measured in a Radiometer Copenhagen PHM240 pH/ion meter. The final percentage of EtOH was always 50% (v : v).

Measurements. UV-Vis absorption spectra were recorded in a Varian Cary 100 Bio or Varian Cary 5000 spectrophotometers. The stopped-flow experiments were conducted in an Applied Photophysics SX20 stopped-flow spectrometer provided with a PDA.1/UV photodiode array detector.

Data analysis and fitting. All pK_a values were determined from the absorbance versus pH experimental data. The observed rate constants were obtained fitting the absorbance versus time data to the integrated first order rate equation. The thermodynamic and kinetic results were globally fitted to the reported equations using the Solver tool in an Excel spreadsheet.

Acknowledgements

This work was supported by the Associated Laboratory for Sustainable Chemistry-Clean Processes and Technologies-LAQV which is financed by national funds from FCT/MEC (UID/QUI/50006/2013) and co-financed by the ERDF under the PT2020 Partnership Agreement (POCI-01-0145-FEDER-007265). NB gratefully acknowledges the post-doctorate grant from the FCT/MEC (SFRH/BPD/84805/2012). SC, MD and TG gratefully acknowledge the CNRS and University Paul Sabatier for financial support. TG thanks the Agence Nationale de la Recherche (ANR-13-BS07-0017-02 ChOZe) for a Post-Doc fellowship. SC also wishes to thank Raymond BROUILLARD for his mentorship in flavylium chemistry.

Notes and references

1. For representative reviews or chapter books dealing with anthocyanins, see: (a) F. Pina, V. Petrov and C. A. T. Laia, Dyes Pigm., 2012, 92, 877; (b) K. Yoshida, K.-i. Oyama and T. Kondo, in Recent Advances in Polyphenol Research, ed. V. Cheynier, P. Sarni-Manchado and S. Quideau, Wiley-Blackwell, Chichester, 2012, vol. 3, p. 99; (c) R. Brouillard, S. Chassaing, G. Isorez, M. Kueny-Stotz and P. Figueiredo, in Recent Advances in Polyphenol Research, ed. C. Santos-Buelga, M. T. Escribano-Bailon and V. Lattanzio, Wiley-Blackwell, Chichester, 2010, vol. 2, p. 1; (d) K. Yoshida, M. Mori and T. Kondo, Nat. Prod. Rep., 2009, 26, 884; (e) R. Brouillard, S. Chassaing and A. Fougerousse, Phytochemistry, 2003, 64, 1179.
2. For an overview, see the following specific issue devoted to anthocyanins: C. Santos-Buelga, N. Mateus and V. De Freitas, J. Agric. Food Chem., 2014, 62, 29.
3. For representative articles dealing with 3-deoxyanthocyanins, see: (a) J. R. N. Taylor, P. S. Belton, T. Beta and K. G. Duodu, J. Cereal Sci., 2014, 59, 257; (b) C. Petti, R. Kushwaha, M. Tateno, A. E. Harman-Ware, M. Crocker, J. Awika and S. DeBolt, J. Agric. Food Chem., 2014, 62, 1227; (c) L. Wang, L. Dykes and J. M. Awika, Food Chem., 2014, 160, 246; (d) B. Geera, L. O. Ojwang and J. M. Awika, J. Food Sci., 2012, 92, 877; (e) J. M. Awika, L. W. Rooney and R. D. Waniska, J. Agric. Food Chem., 2004, 52, 4388; (f) J. M. Baranac and D. S. Amic, J. Agric. Food Chem., 1990, 38, 2111; (g) J. G. Sweeny and G. A. Iacobucci, J. Agric. Food Chem., 1983, 31, 531; (h) P. Coggon, G. A. Moss, H. N. Graham and G. W. Sanderson, J. Agric. Food Chem., 1973, 21, 727.
4. (a) A. Sousa, V. Petrov, P. Araujo, N. Mateus, F. Pina and V. De Freitas, J. Phys. Chem. B, 2013, 117, 1901; (b) F. Pina, M. J. Melo, C. A. Laia, A. J. Parola and J. C. Lima, Chem. Soc. Rev., 2012, 41, 869; (c) F. Pina, V. Petrov and C. A. T. Laia, Dyes Pigm., 2012, 92, 877; (d) R. Gomes, A. M. Diniz, A. Jesus, A. J. Parola and F. Pina, Dyes Pigm., 2009, 81, 69; (e) F. Pina, M. J. Melo, M. Maestri, P. Passaniti and V. Balzani, J. Am. Chem. Soc., 2000, 122, 4496; (f) P. Figueiredo, J. C. Lima, H. Santos, M. C. Wigand, R. Brouillard, A. L. Maçanita and F. Pina, J. Am. Chem. Soc., 1994, 116, 1249.
5. F. Pina, J. Oliveira and V. De Freitas, Tetrahedron, 2015, 71, 3107.
6. (a) M. Duenas, E. Salas, V. Cheynier, O. Dangles and H. Fulcrand, J. Agric. Food Chem., 2006, 54, 189; (b) R. Brouillard, S. Chassaing and A. Fougerousse, Phytochemistry, 2003, 64, 1179.
7. The general behavior of flavylium compounds is recalled here to guarantee clarity for non-experts in flavylium chemistry.
8. For representative examples dealing with multistate behavior and extensive characterization of monomeric flavylium models, see: (a) F. Pina, R. Gomes, N. Basilio and A. T. Cesar, J. Photochem. Photobiol., A, 2013, 269, 1; (b) F. Pina, J. C. Lima, A. J. Parola and C. A. M. Afonso, Angew. Chem., Int. Ed., 2004, 43, 1525; (c) F. Pina, M. J. Melo, A. J. Parola, M. Maestri and V. Balzani, Chem.–Eur. J., 1998, 4, 2001; (d) F. Pina, M. J. Melo, H. Santos, J. C. Lima, I. Abreu, R. Ballardini and M. Maestri, New J. Chem., 1998, 22, 1093.
9. (a) R. Brouillard, B. Delaporte and J. E. Dubois, J. Am. Chem. Soc., 1978, 100, 6202; (b) R. Brouillard and J. E. Dubois, J. Am. Chem. Soc., 1977, 99, 1359.
10. For a representative example of bell-shaped curve, see Fig. 8A.
11. S. Chassaing, M. Kueny-Stotz, G. Isorez and R. Brouillard, Eur. J. Org. Chem., 2007, 2438.
12. (a) M. Kueny-Stotz, R. Brouillard and S. Chassaing, Synlett, 2012, 2053; (b) A. M. Diniz, C. Pinheiro, V. Petrov, A. J. Parola and F. Pina, Chem.–Eur. J., 2011, 17, 6359; (c) A. R. Katritzky, P. Czerney, J. R. Level and W. Du, Eur. J. Org. Chem., 1998, 2623; (d) G. A. Reynolds and J. A. van Allan, J. Heterocycl. Chem., 1969, 6, 623.
13. For synthetic aspects related to flavylium-based pigments, see: (a) S. Chassaing, G. Isorez-Mahler, M. Kueny-Stotz and R. Brouillard, Tetrahedron, 2015, 71, 3066; (b) S. Chassaing, G. Isorez, M. Kueny-Stotz and R. Brouillard, Tetrahedron Lett., 2008, 49, 6999; (c) M. Kueny-Stotz, G. Isorez, S. Chassaing and R. Brouillard, Synlett, 2007, 1067.
14. For representative applications of flavylium-based pigments, see: (a) F. Pina, J. Agric. Food Chem., 2014, 62, 6885; (b) G. Calogero, A. Sinopoli, I. Citra, G. Di Marco, V. Petrov, A. M. Diniz, A. J. Parola and F. Pina, Photochem. Photobiol. Sci., 2013, 12, 883; (c) R. Jiang, A. Miyamoto, A. Martz, A. Specht, H. Ishibashi, M. Kueny-Stotz, S. Chassaing, R. Brouillard, L. P. De Carvalho, M. Goeldner, J. Nakebura, M. Nielsen and T. Grutter, Br. J. Pharmacol., 2011, 162, 1326; (d) R. Gomes, A. M. Diniz, A. Jesus, A. J. Parola and F. Pina, Dyes Pigm., 2009, 81, 69; (e) M. Kueny-Stotz, S. Chassaing, R. Brouillard, M. Nielsen and M. Goeldner, Bioorg. Med. Chem. Lett., 2008, 18, 4864.
15. For the mathematical treatment of Scheme 3b, see Appendix 1 given in ESI.†.
16. At these pH values, the tautomerization is known to be much faster than hydration.
17. k_−i is relatively small at these pH values.
18. IBX was freshly prepared according to the procedure reported in: M. Frigerio, M. Santagostino and S. Sputore, J. Org. Chem., 1999, 64, 4537.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra12017b

---