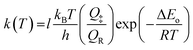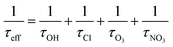Kinetic investigations of chlorine atom initiated photo oxidation reactions of 2,3-dimethyl-1,3-butadiene in the gas phase: an experimental and theoretical study

Abstract

Rate coefficients for the reaction of chlorine atoms with 2,3-dimethyl-1,3-butadiene were measured over the temperature range of 269–393 K by using a relative rate experimental method with reference to isoprene and 1-pentene. Concentrations of the 2,3-dimethyl-1,3-butadiene and reference compounds were monitored by gas chromatography equipped with a Flame Ionization Detector (FID). The obtained rate coefficient for the reaction of 2,3-dimethyl-1,3-butadiene with Cl atoms at 298 K is k = (4.48 ± 0.46) × 10⁻¹⁰ cm³ per molecule per s, which is in good agreement with the reported rate coefficient at 298 K and 760 Torr. The obtained temperature dependent rate coefficient is k_{2,3-dimethyl-1,3-butadiene+Cl} (269–363 K) = (4.59 ± 0.67) × 10⁻¹¹ exp[(663.13 ± 45.8)/T] cm³ per molecule per s. To further understand the reaction mechanism of butadienes with Cl atoms, theoretical calculations were performed for the reactions of 2-methyl-1,3-butadiene (isoprene) and 2,3-dimethyl-1,3-butadiene with Cl atoms as a function of temperature using Conventional Transition State Theory (CTST) in combination with QCISD(T), CCSD(T) and MP2 levels of theory with different basis sets. The theoretically calculated temperature dependent rate coefficient is k_{2,3-dimethyl-1,3-butadiene+Cl} (200–400 K) = (4.12 ± 0.38) × 10⁻¹² exp[(1419.2 ± 26)/T] cm³ per molecule per s which is in excellent agreement with our experimentally measured rate coefficients. The rate coefficient was observed to be increasing with the substitution of hydrogen atoms by methyl groups.

---

Introduction

Butadienes are the most abundant non methane hydrocarbons which are being emitted into the Earth's atmosphere via vegetation and anthropogenic processes.¹ The photo-oxidation of butadienes plays a significant role in the formation of Secondary Organic Aerosols (SOAs) under both low and high NO_x (nitrogen oxides) environments.² It has been estimated that 2-methyl-1,3-butadiene (isoprene) is the single largest source (440–660 TgCyr⁻¹),¹ which is being emitted by the terrestrial biosphere.³ During their photo oxidation, lots of low volatile organic compounds like hydroxycarbonyls, methyl vinylketone, methacrolein and epoxydiols^4,5 are released into the Earth's atmosphere.

Butadienes significantly contribute to the formation of ozone in the troposphere^6,7 because of proliferation and high chemical reactivity in the generation of peroxy radicals.^8,9 The hydroxyl radical initiated oxidation of butadienes establishes the balance of hydrogen oxides (HO_x = OH + HO₂) and influences the urban ozone formation in vegetated areas where biogenic emissions are very high.⁶ Butadienes (1,3-butadiene and 2,3-dimethyl-1,3-butadiene) are widely used in synthetic rubber and textile industries.¹⁰ Butadienes are released into the atmosphere due to incomplete combustion of gasoline and diesel fuels, auto mobile exhausts, plastic or rubber industries,¹¹ petroleum refining and subsequent industries.¹² The kinetic data and complete atmospheric degradation pathways of individual compounds are essential to assess the possible contribution of these compounds to air pollution and climate change. These parameters can be estimated with the measured or computed kinetic parameters of their reactions with the most abundant oxidizing species like OH radicals, Cl atoms and NO₃ radicals in the Earth's atmosphere.

Several groups have measured the rate coefficients for reactions of chlorine atoms with a series of butadienes such as 1,3-butadiene, 2-methyl-1,3-butadiene and 2,3-dimethyl-1,3-butadiene. Ragains et al.¹³ measured the rate coefficients for reactions of chlorine atoms with 1,3-butadiene and 2-methyl-1,3-butadiene (isoprene) to be 4.2 ± 0.4 and (4.6 ± 0.5) × 10⁻¹⁰ cm³ per molecule per s respectively at 298 K and 1 atm pressure using relative rate experimental technique. Notario et al.¹⁴ measured the rate coefficients for the reactions of chlorine atoms with 1,3-butadiene, 2-methyl-1,3-butadiene and 2,3-dimethyl-1,3-butadiene and reported them to be 3.48 ± 0.10, 3.61 ± 0.10 and (3.63 ± 0.14) × 10⁻¹⁰ cm³ per molecule per s respectively at 298 K and 15–60 Torr by using laser photolysis-resonance fluorescence experimental technique. Suh et al.¹⁵ determined the rate coefficient for reaction of chlorine atoms with isoprene and reported to be (4.0 ± 0.3) × 10⁻¹⁰ cm³ per molecule per s at 298 K by using a fast flow reactor coupled with chemical ionization mass spectroscopic (CIMS) technique. Bedjanian et al.¹⁶ measured the rate coefficient for reaction of chlorine atoms with isoprene as a function of pressure and temperature and reported it to be (3.6 ± 0.5) × 10⁻¹⁰ cm³ per molecule per s at 298 K by using discharge-flow mass spectrometric technique.

Although, few groups have measured the rate coefficient for the reaction of chlorine atoms with 2,3-dimethyl-1,3-butadiene at 298 K and 760 Torr but there are no temperature dependent studies till date for the title reaction. To the best of our knowledge, first time we are reporting the temperature dependent rate coefficients for the reaction of chlorine atoms with 2,3-dimethyl-1,3-butadiene. To complement our experimental measurements and to further understand the reaction mechanism of 2-methyl-1,3-butadiene (isoprene) and 2,3-dimethyl-1,3-butadiene with Cl atoms, theoretical calculations were also performed over the temperature range of 200–400 K using Transition State Theory (TST) in combination with QCISD(T), CCSD(T) and MP2 level of theories with different basis sets. Atmospheric implications of these reactions of butadienes with chlorine atoms were discussed and obtained rate coefficients were compared with the reported rate coefficients.

Experimental

Rate coefficients were measured for the reaction of chlorine atoms with 2,3-dimethyl-1,3-butadiene over the temperature range of 269–363 K, using relative rate experimental setup with reference to isoprene¹⁶ and 1-pentene,¹⁷ whose rate coefficients for their reactions with Cl atoms are already known. All the experiments were performed in a double walled Pyrex chamber of 100 cm long (4 cm id.) cell with two inches diameter fused silica windows at the both the ends. The temperature in the reaction chamber was maintained by circulating the cooled/heated fluid through the outer jacket of the cell and was calibrated with a K-type thermocouple within an uncertainty of 2 K in the studied temperature range. Excimer laser (KrF, 248 nm, Coherent Compex Pro) was used to generate chlorine atoms in situ by photolyzing oxalylchloride (COCl)₂. Excimer laser energy was calibrated and ∼6 mJ per pulse per cm² energy was used in these experiments. Reaction mixture was photolyzed by 1000, 1200, 1500, 1800 and 2000 pulses. Concentrations of sample and reference compounds were monitored using the gas chromatograph coupled with FID (Agilent Technologies 7890B, HP-PLOT/Q, 30 m × 0.320 mm × 20.0 μm, 19091P-Q04). The complete experimental setup used in this study has been described previously.¹⁸ The typical concentrations of the reactant and reference compounds were varied between (4–6) × 10¹⁶ molecules per cm³ and that of oxalylchloride was maintained between (4–6) × 10¹⁷ molecules per cm³. Before starting the experiments, some preliminary tests were performed to confirm the wall losses. The reaction mixture was kept in dark for about 3–4 hours which is more than the total reaction time and no significant difference was observed in the concentrations of the samples. The reaction mixture was left idle for some time after each photolysis to ensure the homogeneity. The most important condition in which a standard relative rate technique is valid is when both the substrate molecule and the reference compound compete closely with the oxidant. The ratio of the rate coefficients should vary between 1 and 2.5. The reliability of the measured rate coefficient of the test reaction depends truly on the accuracy with which the rate coefficient of the reference reaction is measured. Temperature dependent rate coefficients for the title reaction were measured by using the below standard relative rate expression.
where [sample]₀, [sample]_t are the concentrations of the sample at times ‘0’ and ‘t’ respectively and [reference]₀, [reference]_t are the concentrations of the reference compounds at times ‘0’ and ‘t’ respectively, k_sample and k_reference are the rate coefficients for the reactions of sample and reference compounds with chlorine atoms. Plot of ln([sample]₀/[sample]_t) versus ln([reference]₀/[reference]_t) gives a straight line with zero intercept and slope gives the ratio of k_sample/k_reference. The rate coefficient for the title reaction at a given temperature was computed using the known k_reference.

Chemicals

2,3-Dimethyl-1,3-butadiene (purity 99.5%, Sigma Aldrich), oxalylchloride (purity 98%, Spectrochem), isoprene (purity 99%, Aldrich), 1-pentene (purity ≥98.5%, Aldrich), nitrogen (99.995%, Indogas Chennai), oxygen (98%, Indogas Chennai). Before using, isoprene, 1-pentene and oxalylchloride were subjected to repeated freeze–pump–thaw cycles.

Computational methodology

The geometries of reactants (2-methyl-1,3-butadiene and 2,3-dimethyl-1,3-butadiene), pre-reactive complexes (RCs), transition states (TSs), product complexes (PCs) and products were optimized at Moller–Plesset second order (MP2)¹⁹ level of theory with different Pople basis sets²⁰ viz. 6-31G(d,p), 6-31+G(d,p) etc. Transition states for all the addition and abstraction channels were identified with one imaginary frequency. Reactants, pre-reactive complexes, product complexes and products were identified with zero imaginary frequencies. All the electronic structure calculations were performed using Gaussian 09 program²¹ suite and all the normal modes and structures were viewed in Gauss view.²² Intrinsic reaction coordinates (IRCs) calculations were carried out at MP2/6-31G(d,p) level of theory for all the transition states to verify that the transition states are actually connected to the reactant and products. Single point energy²³ calculations were carried out at QCISD(T), CCSD(T) level of theories to obtain more refrained and accurate energies.

Results and discussion

Relative rate measurements

Rate coefficients were measured as a function of temperature for the title reaction over the temperature range of 269–363 K with reference to isoprene and 1-pentene. In the present investigation, we used the rate coefficients of isoprene and 1-pentene which were measured by Bedjanian et al.¹⁶ and Coquet et al.¹⁷ respectively by using relative rate experimental setup. Bedjanian et al.¹⁶ reported the temperature dependent rate coefficient is k = (6.7 ± 2.0) × 10⁻¹¹ exp[(485 ± 85)/T] cm³ per molecule per s and Coquet et al.¹⁷ reported it to be k = (4.0 ± 2.2) × 10⁻¹¹ exp[(733.70 ± 288.66)/T] cm³ per molecule per s.

At every temperature, experiments were repeated two to three times to check the reproducibility. The obtained rate coefficients at 269, 285, 298, 310, 330, 350 and 363 K are given in Table 1. For every experiment, the obtained slopes and the errors from the linear least-squares fitting of the data were given. The uncertainties on k_sample/k_reference were found to be 14% (0.15/1.07 with reference to 1-pentene) and 0.8% (0.01/1.14 with reference to isoprene) maximum and minimum respectively. The uncertainties of the rate coefficients at room temperature were calculated by including the quoted errors in the rate coefficients for the reference compounds as the root mean square of the two errors and uncertainties found to be 14% (0.59/4.17) and 8% (0.39/4.8) with reference to isoprene and 1-pentene respectively. At temperatures other than the room temperature, the standard deviations of rate coefficients obtained with reference to isoprene and 1-pentene were taken. The uncertainties on the rate coefficients are 19% and 10% maximum and minimum respectively. Here it should be mentioned that the rate coefficients measured across the studied temperature range with 1-pentene were observed to be larger than the rate coefficients measured with isoprene. The gap between the values of k_average may be due to the large gap between rate coefficients of the reference compounds which were used in our measurements (k_isoprene+Cl = (3.6 ± 0.5) × 10⁻¹⁰ cm³ per molecule per s at 298 K which was measured by Bedjanian et al. and k_1-pentene+Cl = (4.69 ± 0.08) × 10⁻¹⁰ cm³ per molecule per s at 298 K measured by Coquet et al.). Bedjanian et al. used the discharge-flow mass spectrometric method and 0.2 L Pyrex chamber and Cl + Br₂ was the reference reaction. The error associated with Bedjanian et al. reported coefficient is 14%. Coquet et al. used the 3L Pyrex flask equipped with magnetic stirrer and GC-FID with reference to hexane + Cl reaction. The error associated with the Coquet et al. reported coefficient is 1.7%. The difference in measured rate coefficients using two reference compounds may be attributed to the usage of different kind of reaction chambers, detection techniques and the errors associated there in.

Table 1 Relative rate measurements for the reaction of 2,3-dimethyl-1,3-butadiene with chlorine atom over the temperature range of 269–363 K at 760 Torr in N₂ with reference to isoprene and 1-pentene

T (K)	Reference compound	(ksample/kreference) ± 2σ	(ksample/kreference)average ± 2σ	(k ± 2σ) × 10^−10 (cm^3 per molecule per s)	(kaverage ± 2σ) × 10^−10 (cm^3 per molecule per s)	Lite k × 10^−10 (cm^3 per molecule per s) at 298 K
269 ± 2	Isoprene	1.13 ± 0.04	1.12 ± 0.01	4.57 ± 0.01	5.30 ± 1.03
		1.12 ± 0.04
		1.12 ± 0.02
	1-Pentene	0.99 ± 0.03	0.98 ± 0.05	6.03 ± 0.05
		0.96 ± 0.09
		1.01 ± 0.02
285 ± 2	Isoprene	1.12 ± 0.06	1.11 ± 0.02	4.08 ± 0.02	4.68 ± 0.85
		1.10 ± 0.01
	1-Pentene	1.03 ± 0.01	1.00 ± 0.07	5.27 ± 0.07
		0.98 ± 0.01
298 ± 2	Isoprene	1.17 ± 0.02	1.16 ± 0.04	4.17 ± 0.59	4.48 ± 0.46	(3.63 ± 0.14) [Notario et al.]
		1.14 ± 0.01
		1.18 ± 0.04
	1-Pentene	1.07 ± 0.15	1.02 ± 0.08	4.80 ± 0.39
		0.99 ± 0.01
		1.01 ± 0.01
310 ± 2	Isoprene	1.13 ± 0.06	1.08 ± 0.12	3.48 ± 0.12	3.98 ± 0.71
		1.04 ± 0.04
	1-Pentene	1.06 ± 0.05	1.05 ± 0.02	4.48 ± 0.02
		1.04 ± 0.02
330 ± 2	Isoprene	0.97 ± 0.04	1.06 ± 0.25	3.08 ± 0.25	3.40 ± 0.44
		1.15 ± 0.09
	1-Pentene	1.02 ± 0.04	1.00 ± 0.04	3.71 ± 0.04
		0.99 ± 0.02
350 ± 2	Isoprene	1.02 ± 0.03	1.02 ± 0.01	2.73 ± 0.01	3.03 ± 0.40
		1.03 ± 0.05
	1-Pentene	1.06 ± 0.01	1.02 ± 0.11	3.31 ± 0.11
		0.98 ± 0.02
363 ± 2	Isoprene	1.06 ± 0.01	1.03 ± 0.12	2.63 ± 0.12	2.84 ± 0.29
		1.08 ± 0.01
		0.96 ± 0.02
	1-Pentene	0.99 ± 0.07	1.01 ± 0.02	3.04 ± 0.02
		1.01 ± 0.02
		1.03 ± 0.03

---

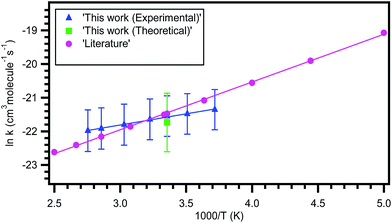
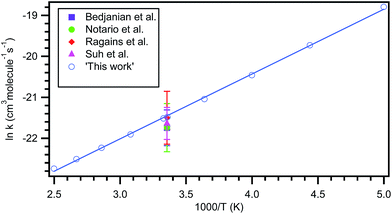
The typical relative rate plot of 2,3-dimethyl-1,3-butadiene with Cl atoms with reference to isoprene and 1-pentene are shown in Fig. 2. The obtained rate coefficient after taking the average of rate coefficients for the title reaction with two references (isoprene and 1-pentene) is k = ((4.48 ± 0.46) × 10⁻¹⁰ cm³ per molecule per s at room temperature and atmospheric pressure. The measured rate coefficients were used to fit the Arrhenius equation using linear least square method and the obtained temperature dependent rate coefficient is k_{2,3-dimethyl-1,3-butadiene+Cl} (269–363 K) = (4.59 ± 0.67) × 10⁻¹¹ exp[(663.1 ± 45.8)/T] cm³ per molecule per s. Slight negative temperature dependence was observed over the measured temperature range and plot is shown in Fig. 1.

Fig. 1 Arrhenius plot of TST rate coefficients calculated at the QCISD/CC-PVDZ//MP2/6-31G(d,p) level of theory between the temperature range of 200 to 400 K and experimentally measured rate coefficients between the temperature range of 269 to 363 K for the reaction of 2,3-dimethyl-1,3-butadiene with Cl atoms.

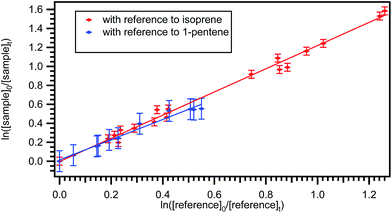Fig. 2 Plot of the relative decrease in the concentration of 2,3-dimethyl-1,3-butadiene due to its reaction with chlorine atoms at 298 K with reference to isoprene and 1-pentene.

Computational

Kinetics. Rate coefficients for the title reaction were calculated using Conventional Transition State Theory (CTST).^24,25
where ‘l’ is the reaction path degeneracy (in present reaction l = 2), ‘k_B’ is Boltzmann constant, ‘T’ is temperature (in Kelvin), ‘h’ is Plank's constant, ‘Q_‡’, and ‘Q_R’ are the partition functions of the transition state and reactant respectively. ‘ΔE_o’ is the molar zero point energy including barrier height and ‘R’ is the universal gas constant.

Energetics and electronic structures

Reaction of Cl atoms with 2,3-dimethyl-1,3-butadiene. Geometries of reactants, transition states and products were optimized at MP2/6-31G(d,p) level of theory and are shown in Fig. 6. All the structural parameters and vibrational frequencies of reactant, RCs, TSs, PCs and products are given in the ESI Tables S.1.1 to S.2.3.† To get more accurate refined energies, single point calculations were performed at QCISD/CC-PVDZ and CCSD/CC-PVDZ level of theories. Rate coefficients obtained at QCISD/CC-PVDZ//MP2/6-31G(d,p) level of theory are observed to be more close to our experimental rate coefficients. 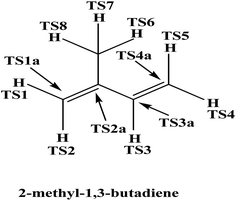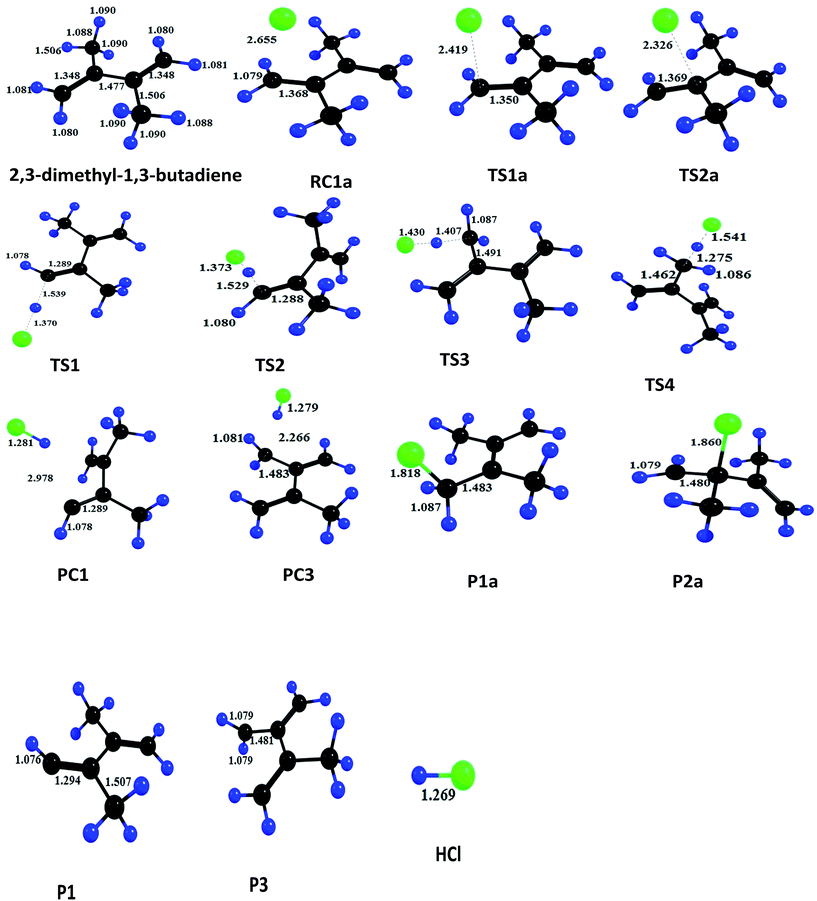Temperature dependent rate coefficients were calculated in the temperature range of 200–400 K with an interval of 25 K and calculated rate coefficients were used to fit the Arrhenius expression and the obtained temperature dependent rate coefficient is k = (4.12 ± 0.38) × 10⁻¹² exp[(1419.2 ± 26)/T] cm³ per molecule per s.

In 2,3-dimethyl-1,3-butadiene, six independent reaction channels via TSs TS1a, TS2a, TS1, TS2, TS3 and TS4 were found. Although, in total it has four addition channels (via TSs TS1a, TS2a, TS3a and TS4a) and ten hydrogen abstraction channels (via TSs TS1 to TS10), both the terminal carbons (via TSs TS1a and TS4a) and other two carbon reaction sites (via TS2a and TS3a) are identical and only two independent addition channels via TSs namely TS1a and TS2a were identified. Abstraction channels going through TS1 and TS10 are found to be identical. Similarly, TS2 and TS9, TS3 and TS8 and TS4, TS5, TS6 and TS7 are identical. Therefore, overall only four independent abstraction channels namely via TS1, TS2, TS3 and TS4 were identified. Hence, in present investigation our discussion is restricted to two addition channels (TS1a and TS2a) and four abstraction channels (TS1, TS2, TS3 and TS4) only. Chlorine addition at terminal carbon (TS1a) and middle carbon (TS2a) leads to the formation of products P1a and P2a (alkyl radicals) respectively. Abstraction of terminal hydrogens via TS1 and TS2 (=CH₂) leads to the formation of products P1 and P2 respectively. Methyl hydrogen (TS3 and TS4) abstractions lead to the formation of products P3 and P4. Upon hydrogen abstraction by chlorine atom, the leaving carbon–hydrogen bonds stretched up to 41%, 42%, 29% and 17% in case of TS1, TS2, TS3 and TS4 respectively when compared with normal –C–H bond in the reactant.

To estimate the feasibility of the title reaction, thermodynamic parameters such as Gibb's free energies (ΔG⁰), enthalpies (ΔH⁰) and entropies (ΔS⁰) were calculated at MP2/6-31G(d,p) level of theory and are tabulated in Table 3. Chlorine addition channels are exothermic and feasible whereas abstractions of hydrogen from terminal carbon (TS1 and Ts2) are endothermic reactions. From thermodynamic data, it is clear that the chlorine atom addition at terminal carbon (TS1a) is more exothermic (ΔH⁰ = −18.4 kcal) and feasible (ΔG⁰ = −10.98 kcal) when compared with chlorine addition at second carbon (TS2a) (ΔG⁰ = −2.59 kcal, ΔH⁰ = −11.35 kcal).

Reaction of Cl atoms with 2-methyl-1,3-butadiene. Temperature dependent rate coefficients were calculated for the reaction of Cl atoms with 2-methyl-1,3-butadiene (isoprene) at QCISD/6-31+G(d,p)//MP2/6-311+G(2df,2p) level of theory over the temperature range of 200–400 K. The geometries of the reactants, pre-reactive complexes, transition states, product complexes and products for all the channels were optimized at MP2/6-311+G(2df,2p) level of theory. Vibrational frequencies and structural parameters for all the geometries are given in the ESI Tables S.3.1 to S.4.4.†

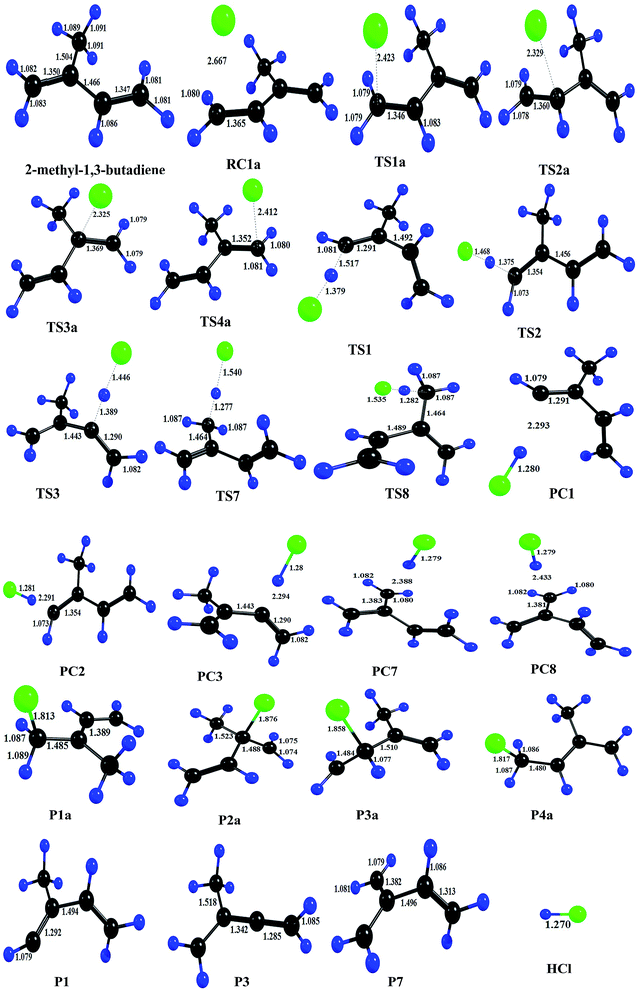
As shown in the above figure, four addition channels namely TS1a, TS2a, TS3a and TS4a and eight hydrogen abstraction channels namely TS1 to TS8 were found in 2-methyl-1,3-butadiene. Hydrogen abstraction channels TS1 and TS5, TS2 and TS4 and TS6 and TS7 are identical. Therefore, nine independent channels (TS1a, TS2a, TS3a, TS4a, TS1, TS2, TS3, TS7 and TS8) were found for the reaction of Cl atoms with 2-methyl-1,3-butadiene. The chlorine addition on the double bond of 2-methyl-1,3-butadiene leads to the formation of chloroalkyl radicals P1a, P2a, P3a and P4a via TS1a, TS2a, TS3a and TS4a respectively. Abstraction of hydrogen atoms forms alkyl radicals P1 to P8 via TS1 to TS8 respectively. The leaving –C–H bond was elongated from 15% to 28% when compared with normal –C–H bond in the case of hydrogen abstraction reactions (Fig. 3).

Fig. 3 Arrhenius plot of TST rate coefficients calculated at the QCISD/6-31+G(d,p)//MP2/6-311+G(2df,2p) level of theory between the temperature range of 200 to 400 K for the reaction of 2-methyl-1,3-butadiene (isoprene) with Cl atoms.

Thermodynamic parameters were calculated to predict the feasibility and spontaneity for the reaction of Cl atoms with 2-methyl-1,3-butadiene and given in Table 7. The most favorable (ΔH⁰ = −19.75 kcal and ΔG⁰ = −11.86 kcal) channel is the addition of chlorine atom at terminal carbon (TS1a). All addition channels (TS1a to TS4a) are more exothermic and feasible. Allylic abstraction reactions (TS7 and TS8) are more feasible when compared with other abstraction reactions. Olefinic hydrogen abstraction reactions (TS1, TS2 and TS3) are more endothermic and less feasible reactions (Table 6).

Rate coefficients. From the potential energy level diagrams (Fig. 4 and 5), relative barrier energies for all the hydrogen abstraction channels were found to be very high when compared with those of chlorine addition reactions. The addition transition states in the title reaction are submerged with reference to the test molecules. Rate coefficients obtained at different level of theories are depicted in Table 2. Chlorine addition at terminal carbon(s) (TS1a) is found to be the most dominant channel by contributing 99% towards the total rate coefficient of the title reaction. The contribution of chlorine addition at terminal carbon (TS1a) towards the total rate coefficient decreases with increase in temperature. The contribution of chlorine addition at second carbon (TS2a) and third carbon (TS3a) towards the total rate coefficient is 0.2% only. The contribution of abstraction channels (TS1, TS2, TS3 and TS4) towards the global rate coefficient is negligible. Although abstraction of allylic hydrogen from the methyl group is thermodynamically more favorable but kinetically its contribution towards the global rate coefficient is negligible (Fig. 7).

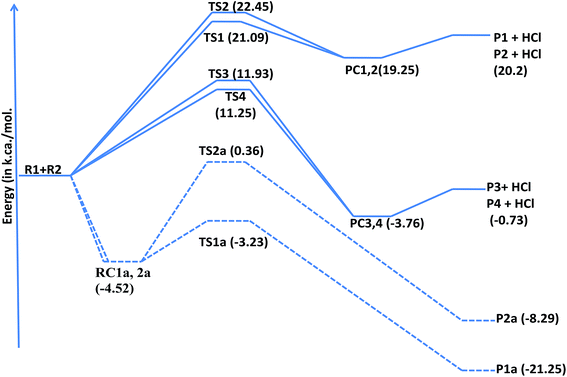Fig. 4 Potential energy level diagram for the reaction of 2,3-dimethyl-1,3-butadiene with chlorine atoms at QCISD/CC-PVDZ//MP2/6-31G(d,p) level of theory.

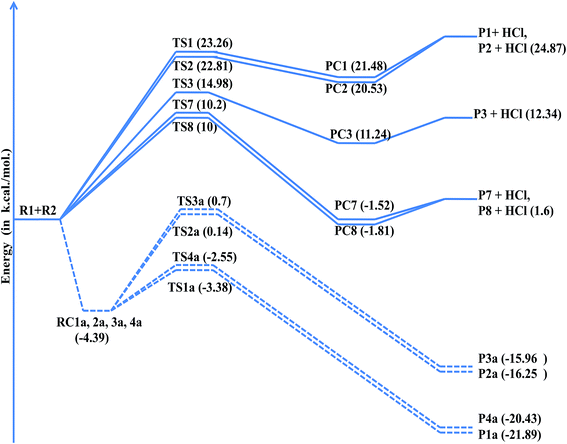Fig. 5 Potential energy level diagram for the reaction of 2-methyl-1,3-butadiene (isoprene) with chlorine atoms at QCISD/6-31+G(d,p)//MP2/6-311+G(2df,2p) level of theory.

Fig. 6 Optimized geometries of the reactants, reactive complexes (RCs), transition states (TSs), product complexes (PCs) and products (Ps) for the reaction of Cl atoms with 2,3-dimethyl-1,3-butadiene. The obtained bond lengths (A⁰) are given on structures computed at MP2/6-31G(d,p) level of theory. Black represents carbon atoms, blue represents hydrogen atoms and green represents chlorine atoms.

Table 2 Calculated total rate coefficients (in cm³ per molecule per s) for the reaction of 2,3-dimethyl-1,3-butadiene + Cl at QCISD/CC-PVDZ//MP2/6-31G(d,p) and CCSD/CCPVDZ//MP2/6-31G(d,p) level of theories

Temperature (K)	k (cm^3 per molecule per s) (QCISD)	k (cm^3 per molecule per s) (CCSD)
200	5.21 × 10^−09	3.38 × 10^−09
225	2.27 × 10^−09	1.57 × 10^−09
250	1.18 × 10^−09	8.32 × 10^−10
275	6.98 × 10^−10	5.09 × 10^−10
298	4.71 × 10^−10	3.56 × 10^−10
300	4.56 × 10^−10	3.42 × 10^−10
325	3.21 × 10^−10	2.46 × 10^−10
350	2.38 × 10^−10	1.86 × 10^−10
375	1.86 × 10^−10	1.48 × 10^−10
400	1.51 × 10^−10	1.21 × 10^−10

---

Fig. 7 Optimized geometries of the reactants, reactive complexes (RCs), transition states (TSs), product complexes (PCs) and products (Ps) for the reaction of Cl atoms with 2-methyl-1,3-butadiene and computed at MP2/6-311+G(2df,2p) level of theory. Black represents carbon atoms, blue represents hydrogen atoms and green represents chlorine atoms.

Rate coefficient obtained for title reaction at 298 K in our computational calculations is k = 4.71 × 10⁻¹⁰ cm³ per molecule per s which is in excellent agreement with our experimentally measured rate coefficient ((4.48 ± 0.46) × 10⁻¹⁰ cm³ per molecule per s). However, the rate coefficients obtained in experimental and computational studies in the present investigation are larger than the one reported by Notario et al.¹⁴ (k = (3.63 ± 0.14) × 10⁻¹⁰ cm³ per molecule per s). This difference may be mainly because their investigations were carried out at very low pressures (15–60 Torr) at 298 K. From Table 2, it is clear that the obtained rate coefficients at QCISD/CC-PVDZ//MP2/6-31G(d,p) level of theory are more closer to the experimentally measured rate coefficients when compared with CCSD/CC-PVDZ//MP2/6-31G(d,p) level of theory. The measured rate coefficients (from 269 to 363 K) exhibit slight negative temperature dependence. Although the theoretically calculated rate coefficients show slightly more negative temperature dependence, they are well within the experimental uncertainties over the studied temperature range. The obtained rate coefficients are plotted and shown in Fig. 1. The Arrhenius parameters are given in Table 5.

Mechanism. In the present investigation, the obtained rate coefficients for the reactions of Cl atoms with 1,3 butadiene, 2-methyl-1,3-butadiene and 2,3-dimethyl-1,3-butadiene are 4.23 × 10⁻¹⁰ cm³ per molecule per s 4.67 × 10⁻¹⁰ cm³ per molecule per s and 4.70 × 10⁻¹⁰ cm³ per molecule per s respectively. There is a systematic increase in the rate coefficients with the methyl substitution. However, the increase is very minimal. In the case of the reactions of these molecules with OH, NO₃ and O₃, the increase is significant with the methyl substitution and this is shown in Table 4. In the reaction of chlorine atoms with 1,3-butadiene, chlorine addition at terminal and middle carbons contribute towards the global rate coefficient by 99.1% and 0.88% respectively. In case of 2-methyl-1,3-butadiene (isoprene), the contributions of chlorine atom addition at terminal carbon (TS1a), second carbon (TS2a), third carbon (TS3a, methyl substituted carbon) and fourth carbon (TS4a) are 89.76%, 0.5%, 0.1% and 9.6% respectively. Whereas, in the reaction of chlorine atoms with 2,3-dimethyl-1,3-butadiene, the contributions of chlorine atom addition at terminal and middle carbons are 99.0% and 0.2% respectively. Chlorine atom addition plays major role in determining the rate coefficients and abstraction reactions seem to be negligible. Kaiser et al.²⁶ observed 9% contribution from abstraction in the case of reactions of chlorine atoms with propene at 700 Torr. Lee and Rowland²⁷ predicted 14% abstraction reaction contribution in propene–chlorine atom reaction at 3000 Torr. In the product analysis of chlorine atom reaction with 2-methyl-1,3-butadiene (isoprene), Ragains and Finlayson-Pitts¹³ predicted that methyl vinyl ketone (MVK) and methacrolein (MACR) as major products along with (13 ± 5.8)% of HCl and (8 ± 6)% of HOCl. Ragains and Finlayson-Pitts predicted that the formation of HCl is due to the addition followed by elimination.

Craig Taatjes²⁸ reviewed the competition between addition and metathesis (direct abstraction or addition followed by HCl elimination) for the reactions of chlorine atoms with alkenes. In the reaction of acetylene with chlorine atoms, they observed that metathesis is considerably endothermic and significant only at high temperatures. Chlorine atom reaction with isoprene is similar to that of propene where abstraction of allylic hydrogen atoms competes with addition reactions across the double bond. Bedjanian et al.¹⁶ measured the yield of HCl as a function of temperature and deduced the rate coefficient for the metathesis by measuring the branching ratios for the reaction of chlorine atoms with isoprene and found its contribution to be less than 10% towards the total rate coefficient. For chlorine atom reaction with alkenes, Ezell et al.²⁹ predicted that the contribution of abstraction channels towards its total rate coefficient to be ∼15–20%. Taatjes et al.²⁸ observed the contribution of metathesis to be increasing towards the total rate coefficient with the temperature.

The chlorine atom addition at terminal and secondary carbon atoms in the test molecules generates tertiary (P1a) and primary (P2a) radicals respectively. The tertiary radical will be further stabilized by conjugation with other carbons which is not possible in the case of primary radical. In addition, steric effect will oppose the addition of Cl atom at substituted carbon there by favoring the formation of P1a. In the product analysis for reaction of 1,3-butadiene with Cl atoms reported by Weihong Wang et al.,³⁰ chlorinated products such as chlorocrotonaldehyde, chloromethyl vinyl ketone were found to be major products, which indicates that chlorine atom addition at terminal carbon is preferred. Earlier studies (Ragains et al.)¹³ of the chlorine atom reactions with simple alkenes show that chlorine atom addition at terminal carbon is much faster than the addition at secondary carbon.

The rate coefficients obtained in the present computational study for the reaction of chlorine atoms with 2-methyl-1,3-butadiene and 2,3-dimethyl-1,3-butadiene are 4.67 × 10⁻¹⁰ cm³ per molecule per s and 4.71 × 10⁻¹⁰ cm³ per molecule per s respectively. In our earlier studies (unpublished data), the rate coefficients from the reaction of 1,3-butadiene with Cl atom was obtained to be 4.23 × 10⁻¹⁰ cm³ per molecule per s. The rate coefficients for the reaction of chlorine atoms with 1,3-butadienes were found to be slightly increasing with methyl substitution. Ragains et al.¹³ observed the same trend for reactions of chlorine atoms with 1,3-butadiene and 2,3-dimethyl-1,3-butadiene. Notario et al.¹⁴ who measured the rate coefficients to be 3.48 ± 0.10, 3.61 ± 0.10 and (3.63 ± 0.14) × 10⁻¹⁰ cm³ per molecule per s for the reactions of chlorine atoms with 1,3-butadiene, 2-methyl-1,3-butadiene (isoprene) and 2,3-dimethyl-1,3-butadiene respectively at 298 K also observed the same trend. This increment in the rate coefficient from 1,3-butadiene to 2,3-dimethyl-1,3-butadiene is due to increasing number of reaction sites (hydrogens) in reactant. This slight increment is attributed to the abstraction of H atoms from the allylic sights, as the removal of an allylic hydrogen atom from the methyl group is more feasible than that of olefinic hydrogen atom. This is evident from the ΔG⁰ values given in Table 3 as well.

Table 3 Barrier heights [ΔE^0‡, kcal mol⁻¹], heat of reaction [ΔH⁰ (298 K), kcal mol⁻¹], Gibbs free energy [ΔG⁰ (298 K), kcal mol⁻¹], and entropy of reaction [ΔS⁰ (298 K), cal mol⁻¹ K⁻¹] for the reaction of 2,3-dimethyl-1,3-butadiene + Cl at QCISD/CC-PVDZ//MP2/6-31G(d,p) level of theory

TSs	ΔE^0‡, kcal mol^−1	ΔH^0, kcal mol^−1	ΔG^0, kcal mol^−1	ΔS^0 cal mol^−1 K^−1
Ts1a	−3.23	−18.40	−10.98	−24.92
Ts2a	−0.36	−11.35	−2.59	−29.38
Ts1	21.09	29.13	26.80	7.82
Ts2	22.45	27.85	25.02	6.86
Ts3	11.93	6.50	3.83	8.95
Ts4	11.25	4.09	1.53	8.58

---

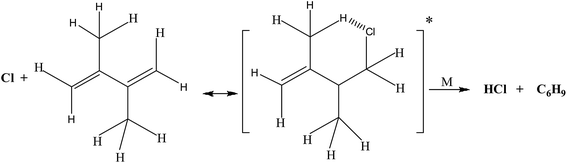
As shown in the above structure, addition of chlorine atom at terminal carbon of the double bond gives a six membered cyclic chloroalkyl radical, from which HCl will be eliminated by the removal of an allylic hydrogen atom from the methyl group. The resulting alkyl radical get stabilized by delocalizing on other double bonded carbons in case of 2,3-dimethyl-1,3-butadiene.

The mechanism of reaction of chlorine atoms with butadienes is analogous to that of the reaction of OH radicals with butadienes. Tuazon et al.³¹ and Baker et al.³² performed the OH initiated photo oxidation of 1,3-butadiene and 2-methyl-1,3-butadiene (isoprene). Based on the end product analysis in the presence of O₂ they predicted that the addition at terminal carbon gives three hydroxyalkyl peroxy radicals which in the presence of (NO)_x form hydroxyalkoxy radicals. These resulting hydroxyalkoxy radicals may decompose or isomerize or react with O₂ to give HCHO, acrolein, methacrolein, methyl vinyl ketone and other unsaturated hydroxycarbonyl compounds as major products accounting for about 65–84% of the total products. Cyclization of the unsaturated 1,4-hydroxyaldehydes with subsequent loss of water was observed which indicates that OH addition was followed by elimination. 1,2- and 1,4-hydroxyalkoxy radicals will be decomposed and the HOCH₂CH=CHCH₂O˙ isomerize via a six membered transition state.

The complete product analysis of chlorine atom reactions with a series of butadienes may give better understanding of these reactions.

Atmospheric implications. Atmospheric lifetime of the test molecule was estimated with respect to its reaction with chlorine atoms in both marine boundary layer (1.30 × 10⁰⁵ molecules per cm³)³³ and ambient conditions (1.00 × 10⁰³ molecules per cm³)³⁴ are 4.5 hours and 24.6 days respectively. The cumulative lifetimes of the butadienes such as 1,3-butadiene, 2-methyl-1,3-butadiene (isoprene) and 2,3-dimethyl-1,3-butadiene were also calculated with reference to OH radicals, Cl atoms, O₃ and NO₃ radicals by using the following expression
where τ_eff is the cumulative life time of the chemical species, τ_OH, τ_Cl, τ_O3 and τ_NO3 are lifetimes of the butadienes due to their reactions with OH radicals,³⁵ Cl atoms (present work), O₃ (ref. 35) and NO₃ (ref. 36) radicals respectively. The global concentrations used in present investigation are 2 × 10⁶ radicals per cm³, 5 × 10⁸ radicals per cm³ and 7 × 10¹¹ molecules per cm³ for OH radical, NO₃ radicals and O₃ molecules^35,36 respectively. The obtained rate coefficients in this investigation are compared with the reactions of the test molecules with other oxidizing species such as OH, NO₃ radicals and O₃ molecules. From Table 4, the first noticeable feature of the data is that the rate coefficients of Cl atoms reactions are typically about ten times faster than the corresponding OH radical reactions. The reactions of Cl atoms with test molecules are in the order of 10⁻¹⁰ cm³ per molecule per s, whereas NO₃ radicals and O₃ molecules reactions are in the order of 10⁻¹³ and 10⁻¹⁸ cm³ per molecule per s respectively. The reactions of Cl atoms with test molecules are much faster when compared with the reactions of OH, NO₃ radicals and O₃ molecules. However, the atmospheric degradation of butadienes with their reactions of Cl atoms is less when compared with OH radicals and NO₃ radicals. This is due to concentrations of Cl atoms are lower than the OH radicals and NO₃ radicals in the atmosphere. However, the atmospheric lifetimes of butadienes are relatively short which suggest their insignificant impact to the global warming of the Earth.

Table 4 Atmospheric lifetimes (τ) calculated for the reactions of butadienes with different atmospheric oxidizing agents

Molecule	Cl atoms		OH radicals^a		NO3 radicals^b		O3 radicals^a		Cumulative life times
	kCl × 10^10	τ (h)	kOH × 10^11	τ (h)	kNO3 × 10^13	τ (h)	kO3 × 10^18	τ (h)	τeff (h)
a Atkinson et al. (2003).b Zhao et al. (2011).c Our earlier work.d This work.
1,3-Butadiene	4.23^c	5	6.66	2	1.24	4.5	6.3	62.9	1.06
2-Methyl-1,3-butadiene	4.67^d	4.6	10.0	1.4	6.24	0.9	12.7	31.2	0.48
2,3-Dimethyl-1,3-butadiene	4.70^d	4.5	12.2	1.2	14.1	0.4	26	15.3	0.27

---

Table 5 Arrhenius parameters obtained for the reaction of chlorine atoms with a series of butadienes in the temperature range of 200–400 K

Molecule	10^12 × A^a (cm^3 per molecule per s)	Ea/R^a (K)
a The quoted uncertainties are 2σ (95% confidence limit).b Our earlier work.c This work.
1,3-Butadiene^b	4.13 ± 0.3	−1385 ± 21
2-Methyl-1,3-butadiene^c	2.37 ± 0.28	−1583 ± 33
2,3-Dimethyl-1,3-butadiene^c	4.12 ± 0.38	−1419 ± 26

---

Table 6 Calculated total rate coefficients (in cm³ per molecule per s) for the reaction of 2-methyl-1,3-butadiene (isoprene) + Cl at QCISD/6-31+G(d,p)//MP2/6-311+G(2df,2p) and CCSD/6-31+G(d,p)//MP2/6-311+G(2df,2p) level of theories

Temperature (K)	k (cm^3 per molecule per s) (QCISD)	k (cm^3 per molecule per s) (CCSD)
200	6.87 × 10^−09	3.62 × 10^−09
225	2.70 × 10^−09	1.54 × 10^−09
250	1.30 × 10^−09	7.90 × 10^−10
275	7.24 × 10^−10	4.64 × 10^−10
298	4.67 × 10^−10	3.54 × 10^−10
300	4.51 × 10^−10	3.02 × 10^−10
325	3.05 × 10^−10	2.12 × 10^−10
350	2.20 × 10^−10	1.58 × 10^−10
375	1.67 × 10^−10	1.23 × 10^−10
400	1.32 × 10^−10	9.99 × 10^−10

---

Table 7 Barrier heights [ΔE^0‡, kcal mol⁻¹], heat of reaction [ΔH⁰ (298 K), kcal mol⁻¹], Gibbs free energy [ΔG⁰ (298 K), kcal mol⁻¹], and entropy of reaction [ΔS⁰ (298 K), cal mol⁻¹ K⁻¹] for the reaction of 2-methyl-1,3-butadiene (isoprene) + Cl at QCISD/6-31+G(d,p)//MP2/6-311+G(2df,2p) level of theory

TSs	ΔE^0‡, kcal mol^−1	ΔH^0, kcal mol^−1	ΔG^0, kcal mol^−1	ΔS^0 cal mol^−1 K^−1
Ts1a	−3.38	−19.75	−11.86	−26.47
Ts2a	0.14	−13.28	−10.52	−25.58
Ts3a	0.70	−14.87	−10.35	−25.69
Ts4a	−2.55	−18.03	−9.92	−27.21
Ts1	23.26	28.28	25.94	6.35
Ts2	22.81	24.53	18.63	6.94
Ts3	14.9	15.70	14.06	5.28
Ts7	10.2	4.53	2.35	7.33
Ts8	10.0	4.53	2.34	7.34

---

Acknowledgements

The authors gratefully acknowledge the Department of Science and Technology (DST), University Grants Commissions (UGC) for their financial support and also we thank Mr V. Ravichandran, High Performance Computing Environment (HPCE), IITMadras for computer resources.

References

1. A. Guenther, T. Karl, P. Harley, C. Wiedinmyer, P. I. Palmer and C. Geron, Atmos. Chem. Phys., 2006, 6, 3181–3210.
2. A. G. Carlton, C. Wiedinmyer and J. H. Kroll, Atmos. Chem. Phys., 2009, 9, 4987–5005.
3. L. Wenfang and Z. Renyi, J. Phys. Chem. A, 2001, 105, 3808–3815.
4. M. Claeys, B. Graham, G. Vas, W. Wang, R. Vermeylen, V. Pashynska, J. Cafmeyer, P. Guyon, M. O. Andreae, P. Artaxo and W. Maenhaut, Science, 2004, 303, 1173–1176.
5. D. S. Jason, W. H. Arthur, N. C. Chana, M. C. Eddingsaasa, L. L. Christine, J. K. Alan, P. H. Scott, C. F. Richard, O. W. Paul and J. H. Seinfeld, PNAS, 2010, 107, 6640–6645.
6. W. L. Chameides, R. W. Lindsay, J. Richardson and C. S. Kiang, Science, 1988, 241, 1473–1475.
7. D. J. Jacob and S. C. Wofsy, J. Geophys. Res., 1988, 93, 1477–1486.
8. R. Atkinson, D. L. Baulch, R. A. Cox, R. F. Jr Hampson, J. A. Kerr, M. J. Rossi and J. Troe, J. Phys. Chem. Ref. Data, 1997, 26, 1329–1499.
9. J. H. Seinfeld and S. N. Pandis, Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, John Wiley & Sons, New York, 1997.
10. D. A. Contos, M. W. Holdren, D. L. Smith, R. C. Brooke, V. L. Rhodes and M. L. Rainey, J. Air Waste Manage. Assoc., 1995, 45, 686–694.
11. E. M. Ward, J. M. Fajen, A. M. Ruder, R. A. Rinsky, W. E. Halperin and C. A. Fesslerbesch, Environ. Health Perspect., 1995, 103, 598–603.
12. Y. Ye, I. E. Galbally, I. A. Weeks, B. L. Duffy and P. F. Nelsona, Atmos. Environ., 1998, 32, 2685–2692.
13. M. L. Ragains and B. J. Finlayson-Pitts, J. Phys. Chem. A, 1997, 101, 1509–1517.
14. A. Notario, G. Lebras and A. Mellouki, Chem. Phys. Lett., 1997, 281, 421–425.
15. I. Suh and R. Zhang, J. Phys. Chem. A, 2000, 104(28), 6590–6596.
16. Y. Bedjanian, G. Laverdet and G. L. Bras, J. Phys. Chem. A, 1998, 102, 953–959.
17. S. Coquet and P. A. Ariya, Int. J. Chem. Kinet., 2000, 32, 478–484.
18. M. Balaganesh, M. R. Dash and B. Rajakumar, J. Phys. Chem. A, 2014, 118(28), 5272–5278.
19. C. Moller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622.
20. M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269.
21. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, et al., Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford, CT, USA, 2010.
22. I. I. R. Dennington, T. Keith, J. Millam, K. Eppinnett, W. L. Hovell and R. Gilliland, GaussView, Version 3.09, Semichem, Inc., Shawnee Mission, KS, 2003.
23. A. Rodriguez, D. Rodriguez, A. Garzon, A. Soto, A. Aranda and A. Notario, Phys. Chem. Chem. Phys., 2010, 12, 12245–12258.
24. M. R. Wright, Fundamental Chemical Kinetics and Exploratory Introduction to the Concepts, Ellis Horwood, Chichester, 1999.
25. M. R. Dash and B. Rajakumar, Atmos. Environ., 2014, 99, 183–195.
26. E. W. Kaiser and T. J. Wallington, J. Phys. Chem., 1996, 100, 9788–9793.
27. F. S. C. Lee and F. S. Rowland, J. Phys. Chem., 1977, 81, 1222–1229.
28. C. A. Taatjes, Int. Rev. Phys. Chem., 1999, 18, 419–458.
29. M. J. Ezell, W. Wang, A. A. Ezell, G. Soskin and B. J. Finlayson-Pitts, Phys. Chem. Chem. Phys., 2002, 4, 5813–5820.
30. W. Wang and B. J. Finlayson-Pitts, Geophys. Res. Lett., 2000, 27, 947–950.
31. E. C. Tuazon, A. Alvarado, S. M. Aschmann, R. Atkinson and J. Arey, Environ. Sci. Technol., 1999, 33, 3586–3595.
32. J. Baker, J. Arey and R. Atkinson, Environ. Sci. Technol., 2005, 39, 4091–4099.
33. C. W. Spicer, E. G. Chapman, B. J. Finlayson-Pitts, R. A. Plastridge, J. M. Hubbe, J. D. Fast and C. M. Berkowitz, Nature, 1998, 394, 353–356.
34. H. B. Singh, A. N. Thakur, Y. E. Chen and M. Kanakidou, Geophys. Res. Lett., 1996, 23, 1529–1532.
35. R. Atkinson and J. Arey, Chem. Rev., 2003, 103, 4605–4638.
36. Z. Zhao, S. Husainy and G. D. Smith, J. Phys. Chem. A, 2011, 115, 12161–12172.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra11892e

---