Dielectric constant measurements of thin films and liquids using terahertz metamaterials

Abstract

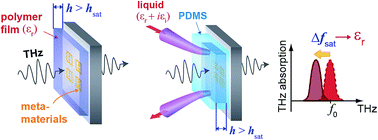
In this paper, we demonstrate that terahertz (THz) metamaterials are powerful tools for determination of dielectric constants of polymer films and polar liquids. As we deposit a dielectric film on a metamaterial, the resonant frequency shifts, but saturates at a specific thickness due to the limited sensing volume of the metamaterial. From the saturated value, we can extract the dielectric constants of various polymers that are transparent to the THz frequency range. In addition, we fabricated a microfluidic channel that contains the metamaterials to address the real dielectric constants for a polar liquid solution. This was possible due to an extremely confined electric field near the gap area of the metamaterials, enabling us to employ very thin liquid layers. We found that the resonance shifts do not depend critically on the imaginary dielectric constants, proving that our approach can be universal in terms of various materials, including absorptive materials. As an example, the dielectric constants of sodium chloride and potassium chloride solutions have been determined with various concentrations. Our experimental findings were successfully confirmed by finite-difference time-domain simulations.

---

Metamaterials have become a fascinating research topic in recent years due to their exotic properties such as super lensing, negative refraction, cloaking, and sensitive sensing.^1–3 They consist of a metallic or semi-metallic structure that interacts with an incident electromagnetic wave.⁴ General metamaterials have a gap structure that works as a capacitor owing to the charge accumulation when a circular current is generated by the incident wave.⁵ As a result, inductive–capacitive (LC) resonance appears in the metamaterials.^6,7 The LC resonant frequency (f₀) of the metamaterials is mainly determined by geometrical parameters such as metal thickness, gap width, length of the side arm, and substrate refractive index.^8–10 More importantly, the LC resonance is highly sensitive to the changes in permittivity in the gap area.^11–14 Dielectric materials located in the gap area induce a change in the resonant frequency, and hence, the metamaterials are ideally suited for sensing dielectric materials.^10,12–14

Terahertz (THz) spectroscopy is widely used in various fields due to its unique applications such as safety inspection, earth-space telecommunication, and sensors.^15,16 In particular, it is desirable to use the THz technique for the examination of biological specimens because THz spectroscopy enables label-free, non-contact, and non-destructive detection.^17–19 However, several chemical and biological substances are transparent to THz waves and do not possess a spectral fingerprint. As a result, it is essential to address their dielectric properties, which are highly restricted for specimens with a low density and thin films. On the other hand, the preparation of a large amount of target materials is usually painstaking. Furthermore, THz waves are strongly attenuated by a water layer and other polar liquid solutions, which is a limitation with practical importance in sensing biological specimens.^18,20

Recently, we found that metamaterials can be used as sensitive biosensors,^10,13 enabling us to detect low-density microorganisms, although their scattering cross-section is extremely low for THz waves.¹³ This is possible because the detection volume is highly confined near the surface, in particular, in the gap area of the metamaterials. The vertical range of the detection volume has been estimated to be 3–4 μm, depending on the detailed geometry of the pattern. As a result, the change in the resonant frequency saturates at a specific thickness (∼10 μm) of target materials deposited on the metamaterials. Therefore, it is highly desirable to use metamaterials to address the dielectric constants of the thin films without necessitating a large amount of the materials. More importantly, the narrow detection range will enable us to study the dielectric properties of various polar liquids that substantially attenuate the THz waves. As we mentioned above, metamaterials sensors were used to detect dielectric materials such as polymer film, and microorganism; however, dielectric constant measurement using metamaterials has not been demonstrated yet.

In this paper, for the first time to our knowledge, we introduce a novel method to extract the dielectric constants of thin polymer films and polar liquid solutions using THz metamaterial sensors through THz time-domain spectroscopy (THz-TDS). We first measure the resonant frequency shift as a function of the film thickness to address the saturation behaviors. We extracted the numerical expression between the resonant frequency shift and the dielectric constant by using the polymer films whose dielectric constants have been determined previously. In addition, we fabricated microfluidic channel devices, incorporating the metamaterial patterns for dielectric constant measurements of the polar liquid solutions with different ion concentrations. Our experimental results were confirmed using finite-difference time-domain (FDTD) simulation results.

The THz transmission amplitudes of THz metamaterial devices were obtained from a conventional THz-TDS system.²¹ Schematic of our THz-TDS system is shown in ESI S1.† A linearly polarized THz pulse was generated from a photoconductive antenna by illuminating with a femtosecond laser at λ = 800 nm. The THz pulse was focused on the THz metamaterials with ∼1 mm² focusing area in ambient conditions. The amplitude and phase of the transmitted THz electric field in time traces were obtained by changing the time delay between the THz pulse and the probe beam. We could obtain the THz spectrum by solving a fast Fourier transform for the transmitted THz electric field in time traces. The THz transmission spectra were measured with an acquisition time of 5 s for each spectrum.

A schematic of the THz metamaterial sensor for the dielectric constant measurement is shown in Fig. 1(a). To fabricate THz metamaterials on a Si substrate (resistivity > 10 000 Ω cm and a thickness of 550 μm), we employed a conventional photolithography technique, followed by metal evaporation of Cr/Au (2 nm/98 nm). The THz metamaterials consisted of a 40 × 40 array of electrical split-ring resonators with a side arm length of 36 μm, line width of 4 μm, gap width of 3 μm, and periodicity of 50 μm.⁵ We monitored the change of the THz transmission through the metamaterial sensors after the deposition of the target materials.

Fig. 1 (a) Schematic of the THz metamaterial device for the measurement of dielectric constants. (b) Schematic of the fluidic THz metamaterial device for the sensing of aqueous solutions. (c) Photograph of the fluidic metamaterial device.

As we spin-coat the polymer with a specific dielectric constant on the metamaterial, the resonant frequency shifts towards a low frequency because of the change in the dielectric configuration of the gap area.^12,13 The resonant frequency shift (Δf) of the metamaterial increases as we increase the thickness of the film, until it saturates. We used the polymer films with known dielectric constant to obtain the numerical expression between Δf and the dielectric constant of the films. Once the saturation condition is attained, we can measure the dielectric constant consistently from Δf without the knowledge of the specimen amounts or the film thickness. This allows us to measure the dielectric constants with very small amounts of target materials as compared to conventional transmission methods without the metamaterial pattern.

We also measured the dielectric constant of a polar liquid solution using fluidic THz metamaterial sensors. We fabricated microfluidic channels using a poly(dimethylsiloxane) (PDMS) fluidic channel, as shown in Fig. 1(b).²² We fixed the channel height of 50 μm, which is significantly larger than the saturation thickness, yet allows sufficient amount of THz wave transmission. The PDMS fluidic channel were prepared by pouring the PDMS onto the SU-8 fluidic channel mold that was fabricated with conventional photo-lithography. A picture of the representative fluidic device is shown in Fig. 1(c). A microscopic image of fluidic metamaterial device can be found in ESI S2.† As discussed above, the THz metamaterial sensors require only thin water layers of thickness less than ∼10 μm because their detection range is highly confined near the surface.¹⁰

We begin with the permittivity measurements of the polymer films using the saturation behaviors of the resonant frequency. In Fig. 2(a), a series of THz transmission spectra have been shown for poly(methyl methacrylate) (PMMA) layers with various thicknesses (h_film) of 1, 2, and 4 μm. The dielectric constant of PMMA films has been measured from THz transmission experiments on the bare Si substrate, which yield 2.56 [ESI S3†]. This is in good agreement with the value found in the literature.²³ We deposited the PMMA layers repeatedly on the metamaterial by spin-coating techniques. As we increase the thickness of the PMMA layer, Δf increases due to the change in the effective dielectric constant of the gap area. In Fig. 2, we quantified Δf as a function of the PMMA layer thickness (h_film). As shown in Fig. 2(b), Δf saturates at a specific thickness (h_sat). This is because the effective sensing volume of the THz metamaterial sensor is highly confined near the surface. We extracted the saturation value Δf_sat using the following exponential fitting: Δf = Δf_sat(1 − exp(−h_film/h_sat)).^10,13,14 A h_sat of 2 μm and Δf_sat of 37 GHz (black dashed line) have been obtained from Fig. 2(b). The resonant frequency (f) with the deposition of the film can be expressed by where ε_eff (=n_eff²) is the effective dielectric constant without the target material in the gap area. From the relation ε = ε_eff + α(ε_r − ε_air), Δf_sat can be expressed by the following relations: Δf_sat/f₀ = α(ε_r − ε_air)/ε_eff, where ε_r and ε_air are the dielectric constants of the film and the air, respectively, and α is the coefficient associated with the sensitivity when h > h_sat.^8–10,13,14

Fig. 2 (a) Transmission amplitudes through THz metamaterials with the deposited PMMA layers for different film thicknesses (h_film). (inset) Optical image of a THz metamaterial. (b) Δf as a function of the thickness of the PMMA layer.

Because it is obvious that Δf_sat/f₀ is determined by ε_r of the medium, our primary goal is to find the explicit relation between the two quantities, when h_film is sufficiently larger than h_sat. We first demonstrate our FDTD simulation results in Fig. 3(a) for films with two different permittivity values. The THz metamaterial sensor is modeled using a Lumerical FDTD simulation to mimic the electromagnetic responses in our experiments.^10,14 Linearly polarized plane wave and periodic boundary condition were used to simulate THz metamaterials on Si substrate. We used THz metamaterial with the same geometrical factors used in the experiments. The metal film was considered as a perfect electric conductor. To imitate the experiments, we used known permittivity values of target materials. FDTD simulation took 15 min for 500 nm sized mesh cell to calculate the electromagnetic response of THz metamaterials.

Fig. 3 (a) FDTD simulation results for Δf as a function of the thickness of the PMMA layer (black) and polyimide layer (red). (b) Δf_sat/f₀ as a function of ε_r for the three polymers extracted from the THz transmission experiments (black boxes) and FDTD simulation results (red solid lines).

As found in the experiments, Δf shows a saturation behavior as a function of the thickness, whereas it is larger for the higher dielectric constants. We plotted Δf_sat/f₀ as a function ε_r in Fig. 3(b) by fitting the simulation data with ten different ε_r's (red solid line). Our fitting curves adequately fit the experimental results plotted together as black boxes, when we used the reported dielectric constants of PMMA (ε_PMMA = 2.56), SU-8 (ε_SU-8 = 2.9), and PI (ε_PI = 3.6).^23–25 Here, the Δf_sat/f₀ of the PMMA is extracted from Fig. 2, whereas those of SU-8 and polyimide (PI) have been added using films with thicknesses of 250 and 100 μm, respectively, which is sufficiently larger than h_sat. We also note that f₀ in the simulation is sometimes different from the experimental value due to fabrication errors; however, they are close to each other in terms of Δf_sat/f₀. Our results validate that the THz metamaterial sensor can measure the dielectric constant of target materials without precise control of the thickness. From the results of Fig. 3(b), we obtained the coefficient α of 0.1886, with which the dielectric constants of various dielectric materials can be determined from the measured Δf_sat. In addition, the sensitivity (S) in terms of refractive index unit (RIU) is found to be 81.4 GHz/RIU for the particular metamaterial pattern used in the experiments.

Our technique of measuring the dielectric constant can be extended to the case of liquid solutions. Owing to the strong attenuation in polar liquids, the measurement of THz optical constants has been only scarcely demonstrated, if any, in the reflection geometries. Conversely, our scheme for the dielectric constant measurement using metamaterial sensors holds for the liquid solution and target materials in aqueous environments. We injected various aqueous solutions such as ethanol, methanol, and distilled water into the fluidic metamaterial device and measured the THz transmission, as schematically shown in Fig. 1(b). Fig. 4(a) shows a series of transmission spectra with the injection of various aqueous solutions, shown together as a black line is the data before injecting the solution into the channel. The resonant frequency shift with respect to air (f₀ = 0.83 THz) was observed, varying with different liquid solutions (ε_ethanol = 2.4 + 0.47i, ε_methanol = 3 + 0.8i, ε_water = 4.8 + 1.98i at 0.8 THz).²⁶ It is obvious that, Δf is higher for large dielectric constants. We note that as the height of the fluidic channel (50 μm) is considerably larger than h_sat, the frequency shift measured here corresponds to Δf_sat, which is useful for extracting ε_r. Fig. 4(b) shows the FDTD simulation results with the dielectric constant values for the series of solutions used in the experiments. Here, we considered both the real and imaginary parts of the known dielectric constants. Interestingly, Δf depends only on the real part of the dielectric constants of aqueous solutions, whereas the imaginary part contributions on Δf is negligible both in experimental and simulation results. However, it is clear, that the strength of the resonance decreases for the solutions with higher imaginary constants.

Fig. 4 Transmission amplitude for the fluidic THz metamaterial sensor with various polar liquids in (a) experiment and (b) FDTD simulation. (c) Δf_sat/f₀ as a function of permittivity in experiment (black) and FDTD simulation (red).

In particular, Δf increases linearly with the real dielectric constants, as shown in Fig. 4(c), in which we plotted Δf_sat/f₀ as a function of ε_r, extracted from the experimental results (black boxes). This is again in a good agreement with the FDTD simulation results (red solid line). Consequently, we can determine the coefficient α of 0.1886 and the sensitivity (which is the same as in Fig. 3), regardless of whether the target materials are solid films or liquid solutions.

Finally, we demonstrate the results of the dielectric constant measurement of ionic solutions. Because ionic solutions such as sodium chloride (NaCl), and potassium chloride (KCl) act as an electrolyte required to sustain our life, it will be very important to address the optical and ac electrical properties for many practical applications;²⁷ however, their dielectric constants in the THz frequency range have been largely unexplored. The dielectric constants of NaCl solutions have been reported by Jepsen et al. in reflection geometry,²⁸ due to the large attenuation loss in transmission geometry as mentioned above. In our work, we obtained the dielectric constant of NaCl solutions with various molar concentrations of 0.25–3.00 M by measuring the frequency shift of the metamaterials. Interestingly, Δf_sat/f₀ of the NaCl solution decreases until the concentration reaches 1 M and rebounds as the concentration increases. The corresponding ε_r are shown in Fig. 5(a), increasing with molar concentrations larger than 1 M. Our results are in good agreement with previous results reported in reflection geometry, although their unique behaviors as a function of the molar concentration has not been understood clearly.²⁸

Fig. 5 Extracted permittivity of (a) NaCl, and (b) KCl solutions for various molar concentrations.

Finally, we measured the dielectric constant of KCl, whose dielectric constant has not been addressed before. Δf_sat/f₀ yields values from 0.08 to 0.11 with respect to air for molar concentrations in the range of 0.25–3.00 M, and the resultant ε_r yields 4.72–3.63 at ∼0.8 THz, as shown in Fig. 5(b). From this result, a linear relationship between ε_r and KCl molar concentration, c, was established: ε_r = −0.38c + 4.82. In contrast to the NaCl case, the dielectric constant decreases with the molar concentration. This behavior has been frequently observed in dc and ac dielectric constants obtained in various frequency ranges, and has been attributed to the excluded volume effects and screening effects of ions.^29,30 To the best of our knowledge, this is the first measurement of THz dielectric constants of a KCl solution with various molar concentrations, and we believe our technique can be extended to dielectric constant measurements of various ionic solutions,³¹ overcoming the current limitations imposed by the strong attenuation of THz waves by polar liquids. We also stress that the THz metamaterial sensor can work as an efficient monitoring tool for ionic concentrations of liquids in microfluidic devices. The sensitivities in terms of the molar concentrations of the KCl solutions yield 10 GHz per M from the results shown above. The sensitivity can be further improved by optimizing the device for aqueous environments, for instance, by changing the geometry of the patterns and substrate configurations.¹⁰

To conclude, we demonstrate the dielectric constant measurements of thin polymer films and polar liquid solutions using THz metamaterials. The resonance shifts of the metamaterials exhibit saturation behaviors with increasing film thickness. The saturation frequency shift varies linearly with the real part of the dielectric constant, from which the numerical expression for the particular metamaterial pattern was extracted. This approach could be very useful for determining the dielectric constants of various materials, without necessitating the large amount of the target material, especially for the transparent materials in the THz regime. More importantly, we were able to measure the dielectric constant of polar liquids such as NaCl and KCl solutions. This was possible due to the unique properties of metamaterials whose detection volume is strongly localized near the surface. In other words, the metamaterials allow us to address the THz optical constants without suffering large attenuation effects in the polar liquids. In addition, we found that the resonance shift does not depend critically on the imaginary part of the dielectric constants, making our approach a universal technique regardless of whether the target specimens are transparent or conductive materials. The results from the FDTD simulation are in good agreement with our experimental results both in the thin film and liquid cases. This work will contribute to the qualitative and quantitative study of the dielectric properties of various types of materials in the THz frequency range.

Acknowledgements

This work was supported by Midcareer Researcher Program (2014R1A2A1A11052108), PRC Program (2009-0094046) through a National Research Foundation grant funded by the Korea Government (MSIP).

References

1. J. B. Pendry, A. J. Holden, D. Robbins and W. Stewart, IEEE Trans. Microwave Theory Tech., 1999, 47, 2075–2084.
2. J. B. Pendry, D. Schurig and D. R. Smith, Science, 2006, 312, 1780–1782.
3. R. A. Shelby, D. R. Smith and S. Schultz, Science, 2001, 292, 77–79.
4. J. T. Hong, D. J. Park, J. H. Yim, J. K. Park, J. Y. Park, S. Lee and Y. H. Ahn, J. Phys. Chem. Lett., 2013, 4, 3950–3957.
5. H. T. Chen, W. J. Padilla, J. M. O. Zide, A. C. Gossard, A. J. Taylor and R. D. Averitt, Nature, 2006, 444, 597–600.
6. H. T. Chen, W. J. Padilla, R. D. Averitt, A. C. Gossard, C. Highstrete, M. Lee, J. F. O'Hara and A. J. Taylor, Terahertz Biomed. Sci. Technol., 2008, 1, 42–50.
7. D. J. Shelton, D. W. Peters, M. B. Sinclair, I. Brener, L. K. Warne, L. I. Basilio, K. R. Coffey and G. D. Boreman, Opt. Express, 2010, 18, 1085–1090.
8. D. J. Park, J. T. Hong, J. K. Park, S. B. Choi, B. H. Son, F. Rotermund, S. Lee, K. J. Ahn, D. S. Kim and Y. H. Ahn, Curr. Appl. Phys., 2013, 13, 753–757.
9. S. J. Park and Y. H. Ahn, J. Korean Phys. Soc., 2015, 65, 1843–1847.
10. S. J. Park, B. H. Son, S. J. Choi, H. S. Kim and Y. H. Ahn, Opt. Express, 2014, 22, 30467–30472.
11. J. Li, C. M. Shah, W. Withayachumnankul, B. S.-Y. Ung, A. Mitchell, S. Sriram, M. Bhaskaran, S. Chang and D. Abbott, Appl. Phys. Lett., 2013, 102, 121101.
12. J. F. O'Hara, R. Singh, I. Brener, E. Smirnova, J. Han, A. J. Taylor and W. Zhang, Opt. Express, 2008, 16, 1786–1795.
13. S. J. Park, J. T. Hong, S. J. Choi, H. S. Kim, W. K. Park, S. T. Han, J. Y. Park, S. Lee, D. S. Kim and Y. H. Ahn, Sci. Rep., 2014, 4, 4988.
14. S. J. Park, S. W. Jun, A. R. Kim and Y. H. Ahn, Opt. Mater. Express, 2015, 5, 2150–2155.
15. J. Federici and L. Moeller, J. Appl. Phys., 2010, 107, 111101.
16. K. Kawase, Y. Ogawa, Y. Watanabe and H. Inoue, Opt. Express, 2003, 11, 2549–2554.
17. M. Tonouchi, Nat. Photonics, 2007, 1, 97–105.
18. A. Menikh, R. MacColl, C. A. Mannella and X. C. Zhang, ChemPhysChem, 2002, 3, 655–658.
19. R. Woodward, V. Wallace, D. Arnone, E. Linfield and M. Pepper, J. Biol. Phys., 2003, 29, 257–259.
20. P. U. Jepsen, U. Møller and H. Merbold, Opt. Express, 2007, 15, 14717–14737.
21. J. T. Hong, K. M. Lee, B. H. Son, S. J. Park, D. J. Park, J. Y. Park, S. Lee and Y. H. Ahn, Opt. Express, 2013, 21, 7633–7640.
22. B. H. Son, J. Y. Park, S. Lee and Y. H. Ahn, Nanoscale, 2015, 7, 15421–15426.
23. Y. S. Jin, G. J. Kim and S. G. Jeon, J. Korean Phys. Soc., 2006, 49, 513–517.
24. N. Ghalichechian and K. Sertel, IEEE Antenn. Wireless Propag. Lett., 2015, 14, 723–726.
25. P. D. Cunningham, N. N. Valdes, F. A. Vallejo, L. M. Hayden, B. Polishak, X. H. Zhou, J. Luo, A. K. Y. Jen, J. C. Williams and R. J. Twieg, J. Appl. Phys., 2011, 109, 043505.
26. J. Balakrishnan, S. Member, B. M. Fischer and D. Abbott, IEEE Photonics J., 2009, 1, 88–98.
27. A. N. Miller and S. B. Long, Science, 2012, 335, 432–436.
28. P. U. Jepsen and H. Merbold, J. Infrared, Millimeter, Terahertz Waves, 2010, 31, 430–440.
29. A. Chandra, J. Chem. Phys., 2000, 113, 903–905.
30. L. Zhao, K. Ma and Z. Yang, Int. J. Mol. Sci., 2015, 16, 8454–8489.
31. M. Galiński, A. Lewandowski and I. Stepniak, Electrochim. Acta, 2006, 51, 5567–5580.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra11777e

---