Computational scrutiny of the effect of N-terminal proline and residue stereochemistry in the nucleation of α-helix fold

Abstract

The biasing of proteins as ordered folds specific to their polypeptide sequences remains unknown in its basis. Several studies of unfolded states in folding–unfolding equilibrium with oligoalanine models have established that the polypeptide structure will unfold as ensembles that largely sample PPII and β-conformations and that the effects internal to the main chain and that of the solvent envelope are critical. While unfolded to largely extended conformations, the folded proteins are a sequence-specific mixture of β and α-conformations. The specificity is unclear in its basis, and we addressed this during the past few years with statistical mechanical studies using appropriate simpler models. In the present study, oligopeptides are used as models to elucidate the effect of N-terminal modification in the sampling of the α-conformation. Specifically, equilibrium sampling of the models for the α-conformation is assessed for dependence on the force field and the effects of specific structure perturbation in the models. Thus, Ac–^LAla₄–NHMe (Ia), Ac–^DAla–^LAla₃–NHMe (Ib), Ac–^LPro–^LAla₃–NHMe (IIa), Ac–^DPro–^LAla₃–NHMe (IIb), Ac–^LPro₂–^LAla₂–NHMe (IIIa), and Ac–^DPro–^LPro–^LAla₂–NHMe (IIIb) are compared as N-terminal alanine or proline and L- or D-residue stereochemically perturbed models. These models are equilibrated in water as an explicit solvent using molecular dynamics, and the ordering of the polypeptide to the α-conformation is tested for the effect of force fields and the specific structural perturbation. The results of molecular dynamics ensembles imply an appreciable shift in the equilibrium sampling of conformations from the β + PPII basin to the α-basin of ϕ, ψ space, including ordering of helical microstates. The results involving well calibrated force fields imply that the ensembles appearing macroscopically as PPII helices have participating microstates that occasionally sample α-basins. We observed the nucleation of an α-helical fold with an N-terminal residue in the ^DPPII conformation in a mixed-L,D structure. The results imply that N-terminal L- to D-residue mutation is the stronger effect that induces folding than N-terminal alanine-to-proline or dialanine-to-diproline mutation. The present study will provide better understanding about the nucleation of helical folds in short peptides and will aid in the design of novel peptides with α-helical structures.

---

Introduction

The ordering of proteins in specificity of their sequences remains a challenge to deciphering the basis.^1–6 The primary challenge is not only the size of proteins but also the thermodynamic systems that order the structures. Ab initio theory is far too complex to easily or directly apply to large and complicated systems. The empirically developed simple force fields are applicable; however, lacking the legitimacy of ab initio theory, they necessitate experimental verification or validation against benchmarks.^7–13 A number of studies using oligoalanines and their solubilized derivatives as the protein main-chain models have established that these models will not unfold as statistical ensembles over the conformational options of polypeptide structures but as structures that are rather well ordered to the PPII conformation.^14–19 We have adopted polyalanines as the structural templates relevant for rigorously addressing the thermodynamics in possible critical issues with rigor.^16,20–23 The issue of the main-chain role was probed by stereochemical perturbation of a natural poly-L structure to alternating-L,D structure. The ordering of main-chain–main-chain hydrogen bonds to β-turn, 3₁₀-helix, and α-helix folds was shown, by mandating the α-conformation in one or more residues, to entail the cost of unfavorable electrostatics in sequence-neighboring peptide units due to the adoption of mutually parallel alignments of the peptide bond dipoles. Does the effect provide for the mediation of conformational selection in protein folding? To address this question, we probed the specific oligoalanine diastereomers with solvents in earlier studies.^20,21 The folding–unfolding equilibrium, specifically in the poly-L structure, turned out to involve two independent solvent effects, (i) screening of electrostatics to allow or disallow α-conformation, and (ii) solvation of peptides to allow or disallow main-chain–main-chain hydrogen bonds. The unfavorable electrostatics of the α-conformation was thus implicated as a possible mediator of α vs. β conformational selection in the folding of the poly-L structure.

The fundamental thermodynamic block in α-helix folding has been a long standing issue much researched and intensely debated. The unfolded proteins were historically thought of as random coils²⁴ and thus the entropy loss in ordering of a chain-length of four to five consecutive residues to an α-conformation was considered as the fundamental thermodynamic cost in the ordering of a helical fold to its first main-chain–main-chain hydrogen bond.^25,26 The unfolded structures are now proven to adopt, at least in localized segments, a PPII helix conformation. The maximization of favorable electrostatics in sequence-neighboring peptides and the interaction of dipoles with solvents is proven to enable the PPII helix to be the minimum of energy. The theory that the PPII helix is the energy minimum in the unfolded structure conflicts with the classical notion that conformational disorder comprises a thermodynamic cost to ordering of the first main-chain–main-chain hydrogen bond of the α-helix structure.

In the present study, using an oligopeptide model, we aim to address the effect of N-terminal proline and residue stereochemistry in the ordering of the α-helical fold. The structures are evolved to equilibrium with molecular dynamics in water as the explicit solvent. The equilibria are resolved to the contributing microstates of the polypeptide structure, which are analyzed on the basis of the conformational specificity and thermodynamic stability of the structures. Alanine is an α-helix-promoting residue;²⁷ however, oligoalanines will order as an α-helix only when they approach or exceed 20 residues in chain-length .²⁸ The structures of long chains (≥20 residues) cannot be rigorously modeled to equilibrium. We circumvent the problem by assessing much shorter chains for the effects of specific structures in the N-terminal residue for possible promotion of helix-folding. As the specificity of the modeled folds can be defined by the force field, we assess three popular force fields before choosing one for the detailed investigation. Consequently, the end-protected oligopeptides are assessed for the dependence of the structure and stability of their specific folds on the force field and the structural changes are applied. The structural changes applied involve mutating N-termini from alanine to proline residues and from L- to D-residues. The alanine-to-proline mutation constrains the rotation in a critical bond of the polypeptide main-chain structure, which may test entropy as a thermodynamic cost in folding. The L- to D-mutation will impose a stereochemical cost on conformational adoption for a residue of the ^Lα_R-conformation; however, it will facilitate the adoption of the inverse proline conformation, viz., the ^DPPII conformation. The adoption of the ^DPPII conformation facilitates the nucleation of the helix by participation in a type II′ β-turn fold, being known as a helix nucleator. The role of D-amino acids in the delineation of the protein folding mechanism is reported in the literature.²⁹ The D-amino acids have been employed to increase the stability of proteins,^30,31 to redesign an active and specific ion channel,³² and in the design of novel folds.^33–37 Recently, Rodriguez-Granillo et al. have shown the stabilizing effect of D-Ala, D-Asn, and D-Gln on the folding free energy of the mini-protein Trp-cage.³⁸

We observed appreciable shifts in the equilibrium sampling of conformations of modeled oligopeptides, from the β + PPII basin to the α-basin of ϕ, ψ space, including the ordering of helical microstates. N-Terminal structure-dependent effects have been observed in the sampling of the α-helical conformation. The present study will enrich our understanding of the nucleation of the α-helical conformation in short peptides, which will help in the design of novel helical peptides. Recent studies highlight the critical role of α-helical structures in the inhibition of disease-relevant intracellular or extracellular protein–protein interactions and in the rational design of biocompatible hydrogels.^39–46

Results

In the present study, we aim to address the effect of N-terminal proline and residue stereochemistry in polyalanine peptides in the nucleation of the α-helical conformation. In pursuing our aim, we have selected the oligoalanines that were long enough to fold and relinquish their PPII conformation, but too short to fold as an α-helix. Polyalanine structures with chain-length greater than four residues are relatively tough to equilibrate computationally; we circumvent the problem by the induction of an α-helix conformation with a specific stereochemical effect in the shorter polyalanine model peptides. The tetraalanine peptides are, therefore, adopted as promising models for addressing the nucleation of the α-helical conformation in an unfolded structure. The study is implemented with end-protected oligopeptides (Ac- at N-terminal and -NHMe at C-terminal) having a chain-length of four residues, varied in their N-terminal residues. The N-termini are alanine or proline and L- or D-residues. Shorter oligoalanines do not adopt stable folds under vacuum or in solvent, as main-chain–main-chain hydrogen bonds are possible only beyond a critical chain-length . The tetra-alanine with terminal blocking groups adopts two main-chain hydrogen bonds of an α-helix fold and three main-chain hydrogen bonds of a 3₁₀-helix fold. The model oligopeptides varying in the structure of the N-terminal residue chosen for the present study are shown in Table 1.

Table 1 The end-protected alanine, proline, and diproline peptides varying in N-terminal residue stereochemistry chosen for molecular dynamics

Model	Oligopeptides
Ia	Ac–^LAla–^LAla–^LAla–^LAla–NHMe
Ib	Ac–^DAla–^LAla–^LAla–^LAla–NHMe
IIa	Ac–^LPro–^LAla–^LAla–^LAla–NHMe
IIb	Ac–^DPro–^LAla–^LAla–^LAla–NHMe
IIIa	Ac–^LPro–^LPro–^LAla–^LAla–NHMe
IIIb	Ac–^DPro–^LPro–^LAla–^LAla–NHMe

---

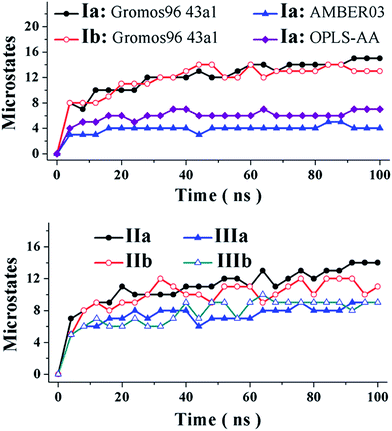
The oligopeptides are submitted to molecular dynamics (MD) simulations in water as explicit solvent. The three specific force fields and specific water models, as described in the computational details, are initially tested with an end-protected tetraalanine. The molecular dynamics trajectories are monitored and assessed in conformational phase space of the polypeptide structure. The peptide conformers were clustered in Cartesian space with a root-mean-square deviation (RMSD) cut-off of 0.15 nm over backbone atoms (N, Cβ, Cα, and C). The peptide conformers were clustered using the GROMACS package with the clustering algorithm developed by Daura et al.,⁴⁷ which is widely used for conformational clustering.⁴⁸ The central member in each cluster is taken to model a microstate, viz., a discrete fold populating the equilibrium. The oligopeptides are compared in the evolution of microstates during molecular dynamics simulations, as shown in Fig. 1. The oligopeptides are noted to achieve equilibrium early and saturate to defined populations in microstates.

Fig. 1 The evolution of microstates over end-protected oligopeptides, the tetra-alanine peptide of poly-L (Gromos96 43a1, AMBER03 and OPLS-AA force fields), a mixed-L,D structure (upper panel), and proline and diproline peptides of poly-L, a mixed-L,D structure (lower panel), during molecular dynamics simulations with water as explicit solvent. The Y-axis represents the number of microstates and the X-axis represents the molecular dynamics simulation time in ns.

The ensembles are compared as macrostates and over the microstates, equivalent to conformational clusters, of the polypeptide structure. The macrostates are assessed in distribution of the radius-of-gyration (R_g) and mean R_g over the populated conformers, in occupancies of specific ϕ, ψ basins, and in percentage occurrence of specific main-chain–main-chain hydrogen bonds, including short-range (SR), medium-range (MR), and long-range (LR) hydrogen bonds. The SR hydrogen bond encompasses a γ-turn; the turn enclosing a residue in the semi-extended conformation does not mandate an α-conformation and tends to be more frequently associated with unfolded than folded polypeptide structures. The MR hydrogen bond encompasses β-turn and α-helix folds and mandates one or two intervening residues (in β-turns) or all participating residues (in helical folds) in the α-conformation. The LR hydrogen bond encompasses β-sheet structures; in oligoalanines this involves typical hairpin folds that encompass residues of mixed conformation, one or two in the β-turn having an α-conformation and the remaining residues being in a β-conformation.

Effect of force fields on the conformational sampling of end-protected tetraalanine

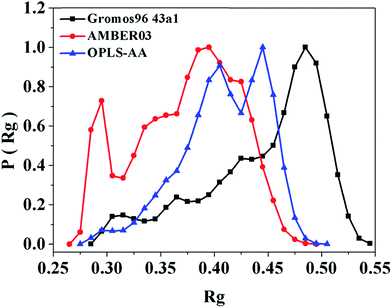
We assess three popular force fields using end-protected tetraalanine with a poly-L structure (Ia). As we note in Table 2, Gromos96 43a1 promotes a significantly greater number of microstates, i.e. 15, compared to AMBER03 and OPLS-AA, i.e. 4 and 7. The mole fraction in the most-populated microstate, as evident from the percent population listed in Table 2, is the highest, i.e. ∼0.8, with OPLS-AA and the lowest, i.e. ∼0.6, with the Gromos96 43a1 force field. Accordingly, the minimum of energy, as noted in Table 2, acquires the greatest thermodynamic stability with OPLS-AA and the lowest with Gromos96 43a1. AMBER03 promotes more compact folds, as evident from the R_g distribution in the macrostate and in the top microstate, reported in Table 2 and shown in Fig. 2. The basis of this is clearly the promotion of the macrostate to relatively higher occupancy in the α-basin, as shown in Fig. 3 and reported in Table 2. From the statistics of basin occupancy reported in Table 2, all force fields are noted to promote the highest occupancy in the PPII-basin; however, this varies significantly from low, i.e. ∼37%, with AMBER03 and high occupancy, i.e. ∼47%, with OPLS-AA. Similar differences in the occupancies of the α- and β-basins are observed. AMBER03 promotes the highest, i.e. ∼24%, occupancy in the α-basin and OPLS-AA promotes the lowest, i.e. ∼13% occupancy, in the α-basin. The occupancy in the β-basin is highest, i.e. ∼40%, with Gromos96 43a1 and lowest, i.e. ∼24%, with AMBER03. Correlated with the promotion of the α-conformation, AMBER03 promotes the highest number of hydrogen bonds per fold and a smaller proportion of SR hydrogen bonds and, correspondingly, a higher proportion of MR hydrogen bonds, as reported in Table 2.

Table 2 Population statistics, free energy of microstates, specific structural and conformational properties of macrostates of end-protected alanine, proline, and diproline peptides varied in N-terminal residue stereochemistry

Model	Force field	N^a	% Pop. in m1^b	ΔG^c	Rg (nm)		% occupancy in M^d			Hydrogen bonds in M^d
					M^d	m1^b	α^e	β^e	PPII^e	Avg./Conf.	% SR^f	% MR^f	% LR^f
a N: total number of microstates.b m1: first microstate (most-populated).c ΔG (kJ mol^−1) = −RT ln K, with K determined by mole fraction in m1.d M: macrostate.e Basin definitions are, α: ^L/Dϕ = −/+20 to −/+100. ^L/Dψ = −/+20 to −/+80; β: ^L/Dϕ = −/+90 to −/+170, ^L/Dψ = +/−80 to +/−180; PPII: ^L/Dϕ = −/+30 to −/+90, ^L/Dψ = +/−80 to +/−170.f Hydrogen bonds are short-range (SR; i → i ± 2), medium-range (MR; i → i ± 3, i → i ± 4) and long-range (LR; i → i ± 5, i → i ± ≥6), according to the sequence separation between the donor and acceptor residues.
Ia	Gromos96 43a1	15	61.1	−1.1	0.45 ± 0.06	0.48 ± 0.02	14.7	39.0	43.2	0.1	32.5	66.9	0.6
	AMBER03	4	74.6	−2.7	0.37 ± 0.05	0.38 ± 0.04	24.2	23.6	36.9	0.2	10.3	89.7	0.0
	OPLS-AA	7	80.2	−3.6	0.41 ± 0.04	0.41 ± 0.04	13.3	31.9	47.0	0.1	34.8	64.7	0.5
Ib	Gromos96 43a1	13	56.1	−0.6	0.40 ± 0.06	0.44 ± 0.03	15.3	36.5	44.2	0.2	27.2	72.2	0.6
IIa	Gromos96 43a1	14	57.6	−0.8	0.44 ± 0.05	0.47 ± 0.03	17.5	27.9	50.2	0.1	37.8	62.2	0.0
IIb	Gromos96 43a1	11	52.2	−0.2	0.38 ± 0.06	0.34 ± 0.03	20.8	25.8	49.5	0.3	12.1	87.8	0.0
IIIa	Gromos96 43a1	9	78.4	−3.2	0.46 ± 0.04	0.47 ± 0.02	7.5	22.1	69.5	0.0	75.3	24.7	0.0
IIIb	Gromos96 43a1	9	64.1	−1.4	0.40 ± 0.05	0.42 ± 0.03	9.9	21.8	65.7	0.1	34.6	65.4	0.0

---

Fig. 2 The radius-of-gyration (R_g) distribution of end-protected tetraalanine peptide of the poly-L structure over conformers defining the macrostate with Gromos96 43a1, AMBER03 and OPLS-AA force fields. The Y-axis represents the distribution of R_g over conformers sampled during molecular dynamics simulation and the X-axis represents R_g in nm.

Fig. 3 The ϕ, ψ spread and preferential basin occupancies of the macrostate over the end-protected tetraalanine peptide of the poly-L structure during molecular dynamics simulation with Gromos96 43a1, AMBER03 and OPLS-AA force fields.

A stick representation of the top three microstates populating specific ensembles, with percent populations shown in parenthesis and ϕ, ψ plots shown underneath, are presented in Fig. 4. All energy minima are PPII helices, conforming to the current insights indicating that the maximization of favorable electrostatics in mutual antiparallel arrangements of peptide dipoles, and the maximization of their solvation, allows the PPII helix to be the minimum of energy for at least the local segments of the polypeptide chain structure. All ensembles in the populated microstates are ordered in one or more residues to the α-conformation, with or without the participation of main-chain–main-chain hydrogen bonds. Specifically, AMBER03 promotes a second microstate as a 3₁₀-helix with two main-chain–main-chain hydrogen bonds, as shown in Fig. 4. The dielectric effect of the water solvent may promote the excursion of one or more residues to an electrostatically unfavorable α-conformation. The role of water as a bridge between hydrogen-bonding groups of polypeptide structures may explain the ordering of specific microstates to the α-conformation without involving main-chain–main-chain hydrogen bonds.^49–52

Fig. 4 The central member of the three most-populated microstates (m₁, m₂, and m₃) of the end-protected tetraalanine peptide of the poly-L structure, populated with Gromos96 43a1 (upper panel), AMBER03 (middle panel) and OPLS-AA (lower panel) force fields is shown in stick representation. The hydrogen bonds among the NH and C=O groups are shown as purple dashed lines. The percent population of each microstate is shown in parenthesis and ϕ, ψ plots for folds are shown underneath the stick models.

The results obtained with AMBER03 depart from other force fields in promoting the 3₁₀-helix to nearly a quarter mole fraction as the second microstate of the ensemble, as shown in Fig. 4. This is at variance with the conclusion from diverse reported studies that short oligoalanines are practically fully ordered PPII helices, mainly due to maximization of favorable electrostatics over peptide dipoles and maximization of the dipoles in solution.⁵³ Overall, the consensus of the present results, involving well-calibrated force fields, implies that ensembles appearing macroscopically as PPII helices may have participating microstates occasionally sampling α-basins. The three independent effects of water as solvent are relevant to enforcing or facilitating the excursions. The screening of the electrostatics of the α-conformation may be an effect that facilitates the excursions. The participation of water molecules in hydrogen-bonded bridges may enforce folds, even in the absence of main-chain–main-chain hydrogen bonds.^49–52 The strength of the water dipole may passively allow main-chain–main-chain hydrogen bonds between peptides to be appreciably stronger dipoles than water. With solvent-promoted diversification, the conformational entropy may be a small but nontrivial cost in folding, while with the dielectric effect of the solvent, the electrostatics of the α-conformation may be a diminished but significant cost in the folding of the PPII helix. We have chosen the Gromos96 force field for investigation of the conformational landscape of the oligopeptide model, as it has been widely used for conformational analysis of peptides in a number of recent studies.⁵⁴ The replica exchange simulations of the (AAQAA)₃ peptide with three different force fields, CHARMM22/CMAP, AMBER99SB, and AMBER03, revealed large deviations from experimental data.⁹ CHARMM22/CMAP and AMBER03 overstabilized the helix (95% and 87% helix at 300 K, respectively), whereas AMBER99SB understabilized the helix (2% at 300 K). The α-helical propensity of AMBER99SB⁵⁵ is arguably too low relative to experimental measurements,¹² while the α-helical propensity is too high for the AMBER03 force field.¹³ On the other hand, the OPLS force field was regarded as the best force field for describing microstructures of organic molecules (i.e. liquid benzene).⁵⁶

Effect of N-terminal alanine-to-proline mutation and residue stereochemistry on conformational sampling

Proline is strong with respect to conformational effects. As the side-chain is linked to backbone nitrogen, proline lacks peptide-NH and has restricted rotational freedom of the N–CO bond, viz., in ϕ torsion. Consequently, the residue is restricted to PPII and α-conformations and is precluded from adopting a fully extended β-conformation. Lacking a donor atom for a main-chain–main-chain hydrogen bond and being unfavorable in the sterics of its side-chain structure, proline does not normally occupy internal positions of the α-helix fold but is a relatively high-propensity N-terminal residue. The diproline structure, less common in proteins, is stronger in conformational effects; these effects were described recently by Shamala and coworkers in a comprehensive study.⁵⁷

The diverse roles of proline include the effect of cis–trans isomerism in the Xxx–Pro peptide bond.^58–60 Saha et al. have investigated the conformational states for the diproline segment (^LPro–^LPro) found in 606 protein structures in the non-redundant data set, with an emphasis on the cis and trans states for the Pro–Pro peptide bond.⁵⁷ Their analysis reveals that the cis–cis configuration of the peptide bond is very rare and the trans peptide bond is mostly favored between the diproline segments in protein structures. The analysis and comparison of conformational states with the Xaa–Pro–Yaa sequence reveals that the Xaa–Pro peptide bond exists preferably as the trans conformer rather than the cis conformer. With the N-terminal proline acylated, isomers are possible in the amide bond in our models. In diproline models, isomers are also possible in the peptide bond between prolines. Uniquely for the Xxx–Pro peptide bond, the cis isomer can have appreciable stability and isomerization is relatively modest in activation energy; this effect has been characterized as an interesting slow step in protein folding. Our starting structures were modeled as trans proline isomers; cis isomers may become populated during MD. We assessed the ensembles in proline peptides for possible occurrence of cis proline isomers. According to the results in Fig. 5, no cis proline isomers are found to populate any of the ensembles. Thus, Gromos96 43a1 did not promote proline isomerization during molecular dynamics simulations. Consequently, all our results pertain to trans proline isomers.

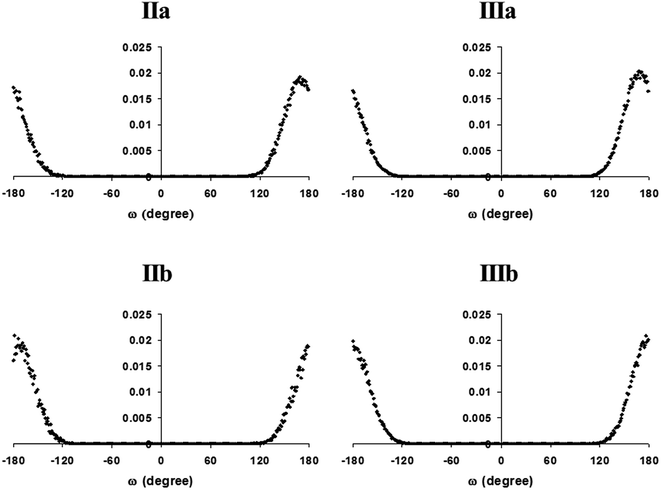Fig. 5 The distribution of ω in conformers populating molecular dynamics ensembles over end-protected proline (IIa, IIb) and diproline (IIIa, IIIb) peptides of poly-L and mixed-L,D structures.

The effects of N-terminal proline and diproline structures are evaluated as a function of L- and D-structures in the N-terminal residue. The poly-L and mixed-L,D tetraalanine are assessed for the effect of mutating N-terminal alanine-to-proline and dialanine-to-diproline structures. From another perspective, alanine, proline, and diproline peptides of the poly-L structure are examined for the effect of N-terminal mutation to the D-structure. The results in Table 2 establish that mutations marginally diminish the number of microstates from 15 and 13 in tetraalanine peptides of poly-L and mixed-L,D structures, to 14 and 11 in proline peptides and 9 each in diproline peptides of specific stereochemical structure. Accordingly, thermodynamic stabilities in minimum-energy folds based on the mole fractions implied in the percent populations given in Table 2 are similar in alanine and proline peptides and marginally greater in diproline peptides. The conformational restriction in one and two of four main-chain N–CO bonds should have a modest, if any, effect on the thermodynamic stability of the minimum-energy fold; however, mutations affect the relative stabilities of folds and thus explain the effects observed macroscopically.

Considering the locked conformation of proline,⁶¹ alanine-to-proline mutation could be expected to promote occupancy of the PPII basin and the α-basin and diminish the occupancy of the β-basin. Conforming to this expectation, alanine-to-proline and dialanine-to-diproline mutations promote a reciprocal change in the occupancy of the PPII basin and the β-basin but increase the occupancy of the α-basin from ∼15% in alanine peptides to ∼20% in proline peptides and, surprisingly, diminish it to <10% in diproline peptides, as noted in Table 2 and shown in Fig. 6. The mean R_g values over macrostates are specific for stereochemistry that is appreciably smaller in mixed-L,D structures, as shown in Fig. 7. The number of hydrogen bonds, although <0.3 per molecule, are higher in mixed-L,D than in poly-L structures, as noted in Table 2. Thus, N-terminal L- to D-residue mutation is the stronger effect in folding the macrostate than N-terminal alanine-to-proline or dialanine-to-diproline mutation.

Fig. 6 The ϕ, ψ spread and preferential basin occupancies of macrostates over end-protected tetraalanine (Ia, Ib), proline (IIa, IIb) and diproline (IIIa, IIIb) peptides of poly-L (upper panel) and mixed-L,D structures (lower panel) during molecular dynamics simulations.

Fig. 7 The radius-of-gyration (R_g) distribution of end-protected tetraalanine (Ia, Ib), proline (IIa, IIb) and diproline (IIIa, IIIb) peptides over conformers defining the macrostate (upper panel) and the most-populated microstate (lower panel). The Y-axis represents the distribution of R_g over conformers sampled during molecular dynamics simulation and the X-axis represents R_g in nm.

The effect of mutation and its basis become clear on examining microscopic folds and their thermodynamic stabilities. The specific folds of poly-L and mixed-L,D structures are compared in Fig. 8 and 9, respectively. The folding follows a similar mechanism in the stereochemical series, as is implied in the ϕ, ψ plots shown underneath, but has contrasting effects on the thermodynamics of folds that depend on stereochemistry, as is evident in the relative populations of folds noted in Fig. 8 and 9. The alanine-to-proline and dialanine-to-diproline mutation does not change the folds or the folding mechanism, which invariably involves isomerization of one or more residues by ∼180° ψ rotation of ^LPPII to the ^Lα-conformation. The effect of isomerizations on the thermodynamics of folds is dramatically stereospecific.

Fig. 8 The central member of four most-populated microstates (m₁, m₂, m₃ and m₄) of end-protected tetraalanine (Ia), proline (IIa) and diproline (IIIa) peptides of the poly-L structure is shown in the stick representation. The hydrogen bonds among NH and C=O groups are shown as purple dashed lines. The percent population of each microstate is shown in parenthesis and ϕ, ψ plots for folds are shown underneath the stick models.

Fig. 9 The central member of four most-populated microstates (m₁, m₂, m₃ and m₄) of end-protected tetraalanine (Ib), proline (IIb) and diproline (IIIb) peptides of mixed-L,D structure is shown as a stick representation. The hydrogen bonds among NH and C=O groups are shown as purple dashed lines. The percent population of each microstate is shown in parenthesis and ϕ, ψ plots for folds are shown underneath the stick models.

As noted in Fig. 8, the PPII helix of the poly-L structure, being ∼0.6 mole fraction of the ensemble in alanine and proline structures and ∼0.8 in the diproline structure, is the minimum of energy in each ensemble. The helix folds by ∼180° ψ rotation in Ala₂ as the second most stable fold in alanine and proline structures with an identical mole fraction of ∼0.2, and by ordering of Ala₄ to the ^Dα-conformation in the diproline structure as the second most stable fold in the ensemble, with a mole fraction of 0.13. The PPII helix folds by ∼180° ψ rotation in Ala₃ to the third most stable fold, with a mole fraction of ∼0.06 in alanine and diproline structures and ∼0.12 in the proline structure. These folds account for a mole fraction of >0.9 in proline and diproline ensembles, but one more fold occurs in the alanine peptide with an appreciable mole fraction of 0.04. The fold is noted to be a helix nucleus (Fig. 8), having three N-terminal residues ordered over two main-chain–main-chain hydrogen bonds from the bifurcated structure to the α-conformation.

As we note in Fig. 9, the PPII helix of the mixed-L,D structure has a mole fraction of 0.64 in the diproline peptide, and 0.56 in alanine peptide, as the most stable fold; however, it has a mole fraction of only 0.38 in the proline peptide, as the second most stable fold in this structure. The PPII helix folds by ∼180° ψ rotation in Ala₂/Pro₂, as the most stable fold in the proline peptide, with a mole fraction of >0.5, and as the second most stable fold in alanine and diproline peptides, with mole fractions close to 0.3. The fold is a type II′ β-turn, according to the hydrogen bonding of the acyl function with Ala₃ NH in the alanine and diproline peptides and according to ϕ, ψ's of Xxx₁ and Xxx₂ residues in all the peptides, as shown in Fig. 10. With Xxx₂ in the α-conformation, the fold is a helix templating structure capable of ordering succeeding residues to the α-conformation. The PPII helix folds by ∼180° ψ rotation in Ala₃ as the third most stable fold in the alanine peptide, with a mole fraction of ∼0.07, and in the diproline peptide, with a mole fraction of ∼0.04. In the proline peptide, the PPII helix folds not only in Ala₃ but also in Ala₂ to the α_R-conformation, with a mole fraction of ∼0.05 of the ensemble. Interestingly, the proline peptide manifests excursion of the PPII helix in steps of ∼180° isomerization into the α-basin, first over Ala₂ and then over both Ala₃ and Ala₂. This is an example of step-by-step propagation of the helical fold.

Fig. 10 The root-mean square (RMS) superposition of specific microstates, m₂ of Ib (dark purple, ∼0.3 mole fraction), m₁ of IIb (blue, ∼0.5 mole fraction), and m₂ of IIIb (cyan, ∼0.3 mole fraction), of end-protected tetraalanine, proline and diproline peptides of mixed-L,D structure, respectively. The identical fold is varied in thermodynamic stability in alanine, proline, and diproline structures.

Discussion

It is by now well proven that the unfolded state of the protein structure is comprised of segments of polypeptide chain structure semi-extended in PPII helix conformation.^7–11 The structure is a close analog of the fully extended β-structure, being an isomer of the PPII structure, related by ∼60° ϕ rotation. Furthermore, it has been shown that the PPII helix and extended β structures are relatives in a thermodynamic sense, since maximization of the hydration of dipoles favors the PPII conformation in water at low temperatures, while maximization of the electrostatics of the peptide dipole in a mutually antiparallel arrangement favors the extended β conformation in water at higher temperatures.⁶² Given thus that the unfolded protein structure is in equilibrium between PPII and β-conformational folds, at least in local segments of the polypeptide chain structure, the fundamental question in protein folding is the folding of the chain to the α-conformation in respect of both the mechanism and thermodynamics of the folding. In a conformational sense, the folding involves a ∼180° ψ rotation between the PPII and α-conformations. The ordering of an isolated residue to the α-conformation, or of a pair of residues to the α-conformation, characterizes folding of the poly-L chains in local β-turns and in hairpin-like folds. While the structures have been targets of intense and incisive research, the critical crux of the protein-folding problem is that of the ordering of consecutive residues to the α-helix conformation. The ordering is a cooperative all-or-none transition and has for this reason been difficult to examine computationally, since the minimal model capable of adopting stable helical folds is too long to permit simulation in order to rigorously address the phenomenon. The question of thermodynamics concerns equilibrium states that are observed macroscopically, while mechanistic considerations involve microscopic interactions. The possible microscopic pathways in the conformational phase space of the polypeptide structure will necessitate analysis with close conjunction between experiment and theory.

Aiming to explore α-helix folding with statistical mechanics, we sought to induce the fold in small oligopeptides stereochemically. Protein residues of the L-structure are similar in ϕ, ψ landscapes, with the exception of L-proline.^63,64 This residue manifests strong avoidance and preference patterns in folded proteins.⁵⁷ Specifically constrained in ϕ to −60° ± 30° and free in ψ like any other L-residue, proline samples with a ^LPPII conformation have ψ = ∼145°, a γ conformation having ψ = ∼75° and an ^Lα_R conformation in the N-terminus of the helical fold having ψ = ∼−45°. However, proline is prohibited from sampling the extended-β conformation that requires ϕ ≥ −120° and the ^Lα_L conformation (the basin in correspondence of the left-handed helical fold) that requires ϕ = ∼60°. Thus, relative to alanine, proline has drastic limits of conformational access.

Proline, diproline, and D-structures were tested as inducers of helix folding. Protein helices are well populated in the N-terminus with proline in the ^Lα_R conformation.⁶⁵ The glycine residue readily accommodates conformational options of L- and D-residues as it lack side-chain and is achiral. Accommodating the ^DPPII conformation, glycine is the principal protein residue in the first corner position of the type II′ β-turn.⁶⁶ The role of glycine has been exploited with the application of D-residues as the inducer of the type II′ β-turn;⁶⁶ the turn has been exploited as a β-hairpin nucleator,⁶⁷ and less commonly as a proto-helix nucleator.^68,69 With the first corner residue locked to the ^DPPII conformation, the type II′ β-turn may serve as a helix N-cap and order second corner residues and succeeding residues to the α-conformation. The L-proline as first helical residue and D-proline as the N-cap residue in the ^DPPII conformation are the recipes⁷⁰ applied for inducement of consecutive β-turns as incipient 3₁₀/α-helix structures and possible helix nuclei.

Specifically, prolines and D-residues were deployed as tests of the “electrostatics” vs. “entropy” theory of protein folding. Constrained in ϕ, proline may induce helix folding entropically and, by adopting the ^DPPII conformation, the D-residue may induce helix folding electrostatically. The end-protected tetraalanine of the poly-L structure was noted to manifest force-field-dependent effects in the equilibrium sampling of the α-conformation. However, on consensus, the PPII helix was found to be the minimum of energy and the α-conformation was sampled partially with each force field. The common effects of participating structures may be involved; the electrostatics of the poly-L structure, the dielectric effect of the solvent, and solvation of peptides may be critical. Surprisingly, substitution of “flexible” alanine with “rigid” proline manifested practically no effect on the conformational diversity of the polypeptide structure.

The molecular dynamics ensembles over alanine, proline, and diproline peptides of poly-L and mixed-L,D structures were comparable in the density of microstates as well as in the stability of minimum-energy folds. Yet, D-proline manifested a strong effect, apparently with no role for entropy. The residue redefined the minimum energy fold (Fig. 10) without affecting the diversity or specificity of the conformation. Thus, minima of energy were distinct folds in D-proline and D-alanine structures. The effect mirrors the role of D-proline as an inducer of helix folds but presents a puzzle regarding its basis.

Clearly, no dramatic effect of the restricted conformation of proline is evident in either the conformational specificity of the ensemble or the thermodynamic stability of the minima of energy. We conclude that proline manifests a surprisingly small effect of its covalent lock relative to alanine in the conformational properties of the ensembles.

These results have suggested a critical role of stereochemistry, not only in energetics, but also in the mechanism of helix folding. Distinct from energetics, the helix-folding mechanism concerns pathways and thus time scales and kinetics of folding. The unfolded protein may populate as interrupted PPII helices, with residues enforced to the α-conformation being critical in pathways of β-sheet and α-helix folding. The PPII helix will require ∼−60° ϕ rotations in ordering to the β-sheet conformation and ∼−180° ψ rotation in ordering to the α-helix conformation. On consensus between force fields, the isomerizations were direct between residue-level structures. While microscopic details differed, the effects relevant to energetics and the mechanism of α-helix folding could be generic to the structures tested in the present study. According to the results obtained with Gromos96 43a1, the N-terminal D-structure residue promoted ordering of the helix in zipper-like isomerizations of ψ. The mechanism is implied, according to which, minimized in energy, the α-helix will fold in a single step by coordinated isomerization of all participating ψs. Considering the electrostatic and desolvation penalty in the folding of barrier-less kinetics,^71–74 the α-helix may manifest a critical role for the solvent as a strong screen of electrostatics and a weak dipolar solvent of peptides.

Conclusion

The ordering of proteins from the unfolded structure to the folded structure in specificity of their sequences remains a challenge to deciphering the basis. The unfolded protein structure is in equilibrium between PPII and β-conformational folds, at least in local segments of the chain structure. The fundamental question in protein folding is that of the folding of the polypeptide chain to the α-conformation in respect of both the mechanism and thermodynamics of the folding. In the present study, end-protected oligopeptides are assessed for the dependence of the structure and stability of their specific folds on the force field and the structural changes involving mutation of N-termini from alanine-to-proline residues and from L- to D-residues. The consensus of the present results, involving well calibrated force fields, implies that the ensembles appearing macroscopically as PPII helices have participating microstates, occasionally sampling α-basins. We observed appreciable shifts in the equilibrium sampling of conformations from the β + PPII basin to the α-basin of ϕ, ψ space, including ordering of helical microstates. In a mixed-L,D structure, nucleation of the helical fold with the N-terminal residue in the ^DPPII conformation is noted in examples involving stepwise propagation of the helix. Thus, N-terminal L- to D-residue mutation is the stronger effect that induces folding than N-terminal alanine-to-proline or dialanine-to-diproline mutation. The results of the present study will provide better understanding about the nucleation of the helical fold in short peptides and will aid in the design of novel short peptides with α-helical structures.

Computational details

Modeling of peptides

The peptides were modeled using the in-house software package, CAPM (Computer Aided Peptide Modeling),³⁴ capable of handling D-amino acids effectively. The in-house program, PDBmake, was used to generate the coordinates of the CAPM modeled structure.

Molecular dynamics simulations and preparation of equilibrium ensembles

The molecular dynamics simulations were performed with the Gromos96 43a1 force field in the GROningen MAchine for Chemical Simulations (GROMACS) 3.3.3 in a periodic box with water as explicit solvent.^75,76 Using ffAMBER ports^77,78 in GROMACS, simulation of Ia was performed with the AMBER03 force field.¹³ An all-atom version of the OPLS force field⁷⁹ available in GROMACS, referred to as OPLS-AA, has been used for simulation of Ia. The TIP3P water model⁸⁰ was used with AMBER03 and OPLS-AA force fields, whereas the SPC water model⁸¹ was used with the Gromos96 43a1 force field. The simulations were performed under NVT conditions, viz., fixed number of particles, constant volume, and constant temperature. The non-bonded list cutoff was 1.4 nm with a shift at 0.8 nm. The integration step was 2 fs. Initial velocities were drawn from a Maxwellian distribution. The temperature was coupled to an external bath with a relaxation time constant of 0.1 ps. The bond lengths were constrained with SHAKE⁸² to a geometric accuracy of 10⁻⁴. The electrostatics were treated by the Particle Mesh Ewald (PME)⁸³ method, implementing a Coulomb cutoff of 1.4 nm, a Fourier spacing of 0.12 nm, and an interpolation order of 4.

The peptides were modeled in the PPII conformation with ϕ^L/D = −/+75° and ψ^L/D = +/−145°. The modeled alanine, proline, and diproline peptides were constrained to the center of a periodic cubic box of edge length 4.4 nm in each case. The model peptides were soaked in water that was added to 1 atm density at 298 K. Firstly, the solute was energy minimized, then the solvent, while restraining the solute, and finally, both were energy-minimized after removing the restraint. The molecular dynamics simulations were initialized and the initial 3 ns trajectory was exempted from the analysis as a pre-equilibration period. The total simulation time was 100 ns for all model peptides. The simulations were performed in multiple runs in parallel and have been merged together to generate the equilibrium in order to avoid the biasness for the starting conformer over the evolution of equilibria. The five different MD simulations of length 20 ns each have been merged together to avoid the biasness for the starting conformer. The trajectories were sampled at 4 ps intervals for all model peptides.

Analysis and characterization of macrostate, polypeptide microstates

Conformational microstates were clustered in Cartesian space with root-mean-square deviation (RMSD) cutoff of 0.15 nm over backbone atoms (N, Cβ, Cα, C), giving microstates diminishing in population, viz., diminishing thermodynamic stability. The clustering was performed in the GROMACS package according to the algorithm by Daura et al.⁴⁷ This procedure has been widely used for conformational clustering in a number of recent studies.⁴⁸ In this procedure, the conformer with the largest number of neighbors was defined as the central member of the first cluster or the most-populated microstate. All members of this microstate were removed from the ensemble, and the procedure was iterated until all the remaining conformers in the ensemble were assigned to specific microstates, diminishing in population. The free energy of the first microstate (most-populated) was estimated using the equation, ΔG = −RT ln K, where R is the gas constant, T is temperature, K = p₁/p_total − p₁, p₁ is the population of the first microstate and p_total is the population of the whole ensemble. We considered the most-populated first microstate as the ordered state and evaluated its stability with regard to the remaining microstates, which were considered as unordered states. The most-populated first microstate was considered as the ordered state because it has maximum thermodynamic stability compared to other microstates. The radius-of-gyration (R_g) was computed using the g_gyrate utility in GROMACS. The percentage occupancy of the macrostate in α, β and PPII basins was computed using the in-house program. The definition of ϕ, ψ basins in the Ramachandran diagram that was adopted in the present study is as follows: α (^L/Dϕ = −/+20 to −/+100, ^L/Dψ = −/+20 to −/+80), β (^L/Dϕ = −/+90 to −/+170, ^L/Dψ = +/−80 to +/−180), and PPII (^L/Dϕ = −/+30 to −/+90, ^L/Dψ = +/−80 to +/−170). The percentage population of specific ϕ, ψ basins was evaluated using in-house written scripts. The hydrogen bonds were enumerated to a 0.35 nm distance (N–O) and a 30° angle (H–N–O) cutoff. The hydrogen bonds are defined as short-range (SR; i → i ± 2), medium-range (MR; i → i ± 3, i → i ± 4) and long-range (LR; i → i ± 5, i → i ± ≥6) according to the sequence separation between donor and acceptor residues.

Acknowledgements

The authors acknowledge the Department of Science & Technology (09DST028), the Government of India for financial support and IIT Bombay, Mumbai for the computing facility “Corona”. Bhupesh Goyal gratefully acknowledges the Science and Engineering Research Board (SERB), Department of Science & Technology, Government of India for the award of his SERB Start-Up Research Grant (Young Scientists) (Sanction No. SB/FT/CS-013/2014).

References

1. Y. Cote, G. G. Maisuradze, P. Delarue, H. A. Scheraga and P. Senet, J. Phys. Chem. Lett., 2015, 6, 1082–1086.
2. S. Sacquin-Mora, J. R. Soc., Interface, 2015, 12, 20150876.
3. K. A. Dill and J. L. MacCallum, Science, 2012, 338, 1042–1046.
4. S. W. Englander and L. Mayne, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 15873–15880.
5. P. G. Wolynes, Biochimie, 2015, 119, 218–230.
6. R. P. Bywater, J. Biomol. Struct. Dyn., 2013, 31, 351–362.
7. R. Raucci, G. Colonna, G. Castello and S. Costantini, Int. J. Pept. Res. Ther., 2013, 19, 117–123.
8. B. R. Brooks, et al., J. Comput. Chem., 2009, 30, 1545–1614.
9. R. B. Best and G. Hummer, J. Phys. Chem. B, 2009, 113, 9004–9015.
10. O. Guvench and A. D. MacKerell Jr, Methods Mol. Biol., 2008, 443, 63–88.
11. W. F. van Gunsteren, J. Dolenc and A. E. Mark, Curr. Opin. Struct. Biol., 2008, 18, 149–153.
12. R. B. Best, N. Buchete and G. Hummer, Biophys. J., 2008, 95, L07–L09.
13. Y. Duan, C. Wu, S. Chowdhury, M. C. Lee, G. Xiong, W. Zhang, R. Yang, P. Cieplak, R. Luo, T. Lee, J. Caldwell, J. Wang and P. Kollman, J. Comput. Chem., 2003, 24, 1999–2012.
14. J. Makowska, S. Rodziewicz-Motowildo, K. Baginska, J. A. Vila, A. Liwo, L. Chmurzynski and H. A. Scheraga, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 1744–1749.
15. D. Wang, B. Jaun and W. F. van Gunsteren, ChemBioChem, 2009, 10, 2032–2041.
16. V. Ramakrishnan, R. Ranbhor and S. Durani, J. Am. Chem. Soc., 2004, 126, 16332–16333.
17. J. E. Shea and C. L. Brooks III, Annu. Rev. Phys. Chem., 2001, 52, 499–535.
18. C. L. Brooks III, Acc. Chem. Res., 2002, 35, 447–454.
19. I. H. McColl, E. W. Blanch, L. Hecht, N. R. Kallenbach and L. D. Barron, J. Am. Chem. Soc., 2004, 126, 5076–5077.
20. K. R. Srivastava, A. Kumar, B. Goyal and S. Durani, J. Phys. Chem. B, 2011, 115, 6700–6708.
21. A. Kumar, V. Ramakrishnan, R. Ranbhor, K. Patel and S. Durani, J. Phys. Chem. B, 2009, 113, 16435–16442.
22. V. Ramakrishnan, R. Ranbhor, A. Kumar and S. Durani, J. Phys. Chem. B, 2006, 110, 9314–9323.
23. V. Ramakrishnan, R. Ranbhor, A. Kumar and S. Durani, Biopolymers, 2006, 83, 537–545.
24. C. Tanford, Adv. Protein Chem., 1968, 23, 121–282.
25. B. H. Zimm and J. K. Bragg, J. Chem. Phys., 1959, 31, 526–535.
26. S. Lifson and A. Roig, J. Chem. Phys., 1961, 34, 1963–1974.
27. P. Y. Chou and G. D. Fasman, Biochemistry, 1974, 13, 211–222.
28. A. Chakrabartty and R. L. Baldwin, Adv. Protein Chem., 1995, 46, 141–176.
29. R. M. Culik, S. Annavarapu, V. Nanda and F. Gai, Chem. Phys., 2013, 422, 131–134.
30. B. Anil, B. B. Song, Y. F. Tang and D. P. Raleigh, J. Am. Chem. Soc., 2004, 126, 13194–13195.
31. D. V. Williams, B. Barua and N. H. Andersen, Org. Biomol. Chem., 2008, 6, 4287–4289.
32. F. I. Valiyaveetil, M. Sekedat, R. MacKinnon and T. W. Muir, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 17045–17049.
33. M. D. Struthers, R. P. Cheng and B. Imperiali, Science, 1996, 271, 342–345.
34. S. Durani, Acc. Chem. Res., 2008, 41, 1301–1308.
35. K. Patel, B. Goyal, A. Kumar, N. Kishore and S. Durani, J. Phys. Chem. B, 2010, 114, 16887–16893.
36. B. Goyal, K. Patel, K. R. Srivastava and S. Durani, RSC Adv., 2015, 5, 105400–105408.
37. B. Goyal, K. R. Srivastava, K. Patel and S. Durani, ChemistrySelect, 2016, 1, 2050–2057.
38. A. Rodriguez-Granillo, S. Annavarapu, L. Zhang, R. L. Koder and V. Nanda, J. Am. Chem. Soc., 2011, 133, 18750–18759.
39. Y. Huang, Q. Feng, Q. Yan, X. Hao and Y. Chen, Mini-Rev. Med. Chem., 2015, 15, 73–81.
40. S. E. Miller, P. F. Thomson and P. S. Arora, Current Protocols in Chemical Biology, 2014, 6, 101–116.
41. J. S. Khara, F. K. Lim, Y. Wang, X. Y. Ke, Z. X. Voo, Y. Y. Yang, R. Lakshminarayanan and P. L. Ee, Acta Biomater., 2015, 28, 99–108.
42. T. T. Dinh, D. H. Kim, H. X. Luong, B. J. Lee and Y. W. Kim, Bioorg. Med. Chem. Lett., 2015, 25, 4016–4019.
43. Y. Demizu, T. Misawa, T. Nagakubo, Y. Kanda, K. Okuhira, Y. Sekino, M. Naito and M. Kurihara, Bioorg. Med. Chem., 2015, 23, 4132–4138.
44. M. Pelay-Gimeno, A. Glas, O. Koch and T. N. Grossmann, Angew. Chem., Int. Ed. Engl., 2015, 54, 8896–8927.
45. N. Mehrban, B. Zhu, F. Tamagnini, F. I. Young, A. Wasmuth, K. L. Hudson, A. R. Thomson, M. A. Birchall, A. D. Randall, B. Song and D. N. Woolfson, ACS Biomater. Sci. Eng., 2015, 1, 431–439.
46. K. Estieu-Gionnet and G. Guichard, Expert Opin. Drug Discovery, 2011, 6, 937–963.
47. X. Daura, K. Gademann, B. Jaun, D. Seebach, W. F. van Gunsteren and A. E. Mark, Angew. Chem., Int. Ed. Engl., 1999, 38, 236–240.
48. (a) J. K. Marzinek, R. Lakshminarayanan, E. Goh, R. G. Huber, S. Panzade, C. Verma and P. J. Bond, Sci. Rep., 2016, 6, 19160; (b) G. Rossetti, F. Musiani, E. Abad, D. Dibenedetto, H. Mouhib, C. O. Fernandez and P. Carloni, Phys. Chem. Chem. Phys., 2016, 18, 5702–5706; (c) P. Gupta, B. Liu, D. Klepacki, V. Gupta, K. Schulten, A. S. Mankin and N. Vázquez-Laslop, Nat. Chem. Biol., 2016, 12, 153–158; (d) G. O. Rutter, A. H. Brown, D. Quigley, T. R. Walsh and M. P. Allen, Phys. Chem. Chem. Phys., 2015, 17, 31741–31749; (e) B. Goyal, K. Patel, K. R. Srivastava and S. Durani, RSC Adv., 2015, 5, 105400–105408; (f) Y. Sun, Z. Qian, C. Guo and G. Wei, Biomacromolecules, 2015, 16, 2940–2949; (g) A. K. Somavarapu and K. P. Kepp, ChemPhysChem, 2015, 16, 3278–3289; (h) S. R. Gerben, J. A. Lemkul, A. M. Brown and D. R. Bevan, J. Biomol. Struct. Dyn., 2014, 32, 1817–1832; (i) C. Merten, F. Li, K. Bravo-Rodriguez, E. Sanchez-Garcia, Y. Xu and W. Sander, Phys. Chem. Chem. Phys., 2014, 16, 5627–5633; (j) F. Godschalk, S. Genheden, P. Söderhjelm and U. Ryde, Phys. Chem. Chem. Phys., 2013, 15, 7731–7739.
49. Y. Levy and J. N. Onuchic, Annu. Rev. Biophys. Biomol. Struct., 2006, 35, 389–415.
50. M. Petukhov, D. Cregut, C. M. Soares and L. Serrano, Protein Sci., 1999, 8, 1982–1989.
51. L. Serrano, Adv. Protein Chem., 2000, 53, 49–85.
52. P. B. Law and V. Daggett, Protein Eng., Des. Sel., 2010, 23, 27–33.
53. J. Graf, P. H. Nguyen, G. Stock and H. Schwalbe, J. Am. Chem. Soc., 2007, 129, 1179–1189.
54. (a) J. Lee, I. Kwon, S. S. Jang and A. E. Cho, J. Mol. Model., 2016, 22, 92; (b) A. Kumar, S. Srivastava, S. Tripathi, S. K. Singh, S. Srikrishna and A. Sharma, J. Biomol. Struct. Dyn., 2015, 1–12; (c) L. Baweja, K. Balamurugan, V. Subramanian and A. Dhawan, J. Mol. Graphics Modell., 2015, 61, 175–185; (d) V. Minicozzi, R. Chiaraluce, V. Consalvi, C. Giordano, C. Narcisi, P. Punzi, G. C. Rossi and S. Morante, J. Biol. Chem., 2014, 289, 11242–11252; (e) I. Autiero, E. Langellaa and M. Saviano, Mol. BioSyst., 2013, 9, 2835–2841; (f) F. Liu, X. Dong, L. He, A. P. J. Middelberg and Y. Sun, J. Phys. Chem. B, 2011, 115, 11879–11887; (g) S. T. Ngo and M. S. Li, J. Phys. Chem. B, 2012, 116, 10165–10175; (h) M. H. Viet, S. T. Ngo, N. S. Lam and M. S. Li, J. Phys. Chem. B, 2011, 115, 7433–7446; (i) C. Yang, X. Zhu, J. Li and R. Shi, J. Mol. Model., 2010, 16, 813–821; (j) J. A. Lemkul and D. R. Bevan, Biochemistry, 2010, 49, 3935–3946; (k) C. Yang, J. Li, Y. Li and X. Zhu, J. Mol. Struct.: THEOCHEM, 2009, 895, 1–8.
55. V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Proteins: Struct., Funct., Bioinf., 2006, 65, 712–725.
56. C. Fu and S. X. Tian, J. Chem. Theory Comput., 2011, 7, 2240–2252.
57. I. Saha and N. Shamala, Biopolymers, 2012, 97, 54–64.
58. C. Gratwohl and K. Wuthrich, Biopolymers, 1976, 15, 2025–2041.
59. G. N. Ramachandran and A. K. Mitra, J. Mol. Biol., 1976, 107, 85–92.
60. (a) M. W. MacArthur and J. M. Thornton, J. Mol. Biol., 1991, 218, 397–412; (b) U. Reimer, G. Scherer, M. Drewello, S. Kruber, M. Schutkowski and G. Fischer, J. Mol. Biol., 1998, 279, 449–460; (c) D. Pal and P. Chakrabarti, J. Mol. Biol., 1999, 294, 271–288; (d) R. Bhattacharyya and P. Chakrabarti, J. Mol. Biol., 2003, 331, 925–940; (e) D. Pahlke, C. Freund, D. Leitner and D. Labudde, BMC Struct. Biol., 2005, 5, 8.
61. C. Ramakrishnan and G. N. Ramachandran, Biophys. J., 1965, 5, 909–933.
62. (a) Y. Mu and G. Stock, J. Phys. Chem. B, 2002, 106, 5294–5301; (b) F. Eker, X. Cao, L. Nafie and R. Schweitzer-Stenner, J. Am. Chem. Soc., 2002, 124, 14330–14341; (c) F. Eker, K. Griebenow and R. Schweitzer-Stenner, J. Am. Chem. Soc., 2003, 125, 8178–8185.
63. G. N. Ramachandran, C. Ramakrishnan and V. Sasisekharan, J. Mol. Biol., 1963, 7, 95–99.
64. G. N. Ramachandran and V. Sasisekharan, Adv. Protein Chem., 1968, 23, 283–438.
65. (a) M. K. Kim and Y. K. Kang, Protein Sci., 1999, 8, 1492–1499; (b) T. L. Presta and G. D. Rose, Science, 1988, 240, 1632–1641; (c) J. S. Richardson and D. C. Richardson, Science, 1988, 240, 1648–1652; (d) R. Aurora and G. D. Rose, Protein Sci., 1998, 7, 21–38; (e) K. Gunasekaran, H. A. Nagarajaram, C. Ramakrishnan and P. Balaram, J. Mol. Biol., 1998, 275, 917–932; (f) A. R. Viguera and L. Serrano, Protein Sci., 1999, 8, 1733–1742.
66. G. D. Rose, L. M. Gierasch and J. A. Smith, Adv. Protein Chem., 1985, 37, 1–109.
67. (a) I. L. Karle, S. K. Awasthi and P. Balaram, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 8189–8193; (b) H. E. Stanger and S. H. Gellman, J. Am. Chem. Soc., 1998, 120, 4236–4237; (c) S. H. Gellman, Curr. Opin. Chem. Biol., 1998, 2, 717–725; (d) D. Ramadan, D. J. Cline, S. Bai, C. Thorpe and J. P. Schneider, J. Am. Chem. Soc., 2007, 129, 2981–2988.
68. V. Bobde, S. Beri, S. Rawale, C. V. V. Satyanarayana and S. Durani, Tetrahedron, 1995, 51, 3077–3086.
69. F. Fabiola, V. Pattabhi, S. Rawale, E. B. Raju and S. Durani, Chem. Commun., 1997, 1379–1380.
70. (a) S. Raghothama, S. Aravinda, N. Shamala and P. Balaram, Biopolymers, 2010, 94, 360–370; (b) Kantharaju, S. Raghothama, U. S. Raghavender, S. Aravinda, N. Shamala and P. Balaram, Biopolymers, 2009, 92, 405–416; (c) B. Chatterjee, I. Saha, S. Raghothama, S. Aravinda, R. Rai, N. Shamala and P. Balaram, Chem.–Eur. J., 2008, 14, 6192–6204; (d) R. Rai, S. Aravinda, K. Kanagarajadurai, S. Raghothama, N. Shamala and P. Balaram, J. Am. Chem. Soc., 2006, 128, 7916–7928; (e) Y. V. Venkatachalapathi and P. Balaram, Nature, 1979, 281, 83–84.
71. J. Liu, L. A. Campos, M. Cerminara, X. Wang, R. Ramanathan, D. S. English and V. Muñoz, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 179–184.
72. M. B. Prigozhin and M. Gruebele, J. Am. Chem. Soc., 2011, 133, 19338–19341.
73. S. S. Cho, P. Weinkam and P. G. Wolynes, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 118–123.
74. M. M. Garcia-Mira, M. Sadqi, N. Fischer, J. M. Sanchez-Ruiz and V. Muñoz, Science, 2002, 298, 2191–2195.
75. E. Lindahl, B. Hess and D. van der Spoel, J. Mol. Model., 2001, 7, 306–317.
76. W. F. van Gunsteren, S. R. Billeter, A. A. Eising, P. H. Hünenberger, P. Krüger, A. E. Mark, W. R. P. Scott and I. G. Tironi, Biomolecular Simulation: The GROMOS96 Manual and User Guide, Vdf Hochschulverlag AG an der ETH Zürich, Zürich, Switzerland, 1996, pp. 1–1042.
77. E. J. Sorin and V. S. Pande, Biophys. J., 2005, 88, 2472–2493.
78. A. J. DePaul, E. J. Thompson, S. S. Patel, K. Haldeman and E. J. Sorin, Nucleic Acids Res., 2010, 38, 4856–4867.
79. G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2001, 105, 6474–6487.
80. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
81. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren and J. Hermans, Interaction models for water in relation to protein hydration. Intermolecular Forces, ed. B. Pullman, Reidel Publishing Company, Dordrecht, The Netherlands, 1981, pp. 331–342.
82. J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
83. U. Essmann, L. Perera, M. Berkowitz, T. Darden, H. Lee and L. Pederson, J. Chem. Phys., 1995, 103, 8577–8593.

---

Footnotes

† Department of Chemistry, School of Basic and Applied Sciences, Sri Guru Granth Sahib World University, Fatehgarh Sahib-140406, Punjab, India.

‡ Department of Chemistry, University of Toronto, Toronto, ON, M5S 3H6, Canada.

§ Department of Physics and Astronomy, Michigan State University, East Lansing, USA.

---