A rare doubly nitrato and phenoxido bridged trimetallic CuII complex: EPR, antiferromagnetic coupling and theoretical rationalization†
Amitabha Datta*a,
Kuheli Dasab,
Sandeep B. Manea,
Shruti Mendirattaa,
Mohamed Salah El Fallahc,
Eugenio Garribbad,
Antonio Bauzáe,
Antonio Frontera *e,
Chen-Hsiung Hung*a and
Chittaranjan Sinhab
*e,
Chen-Hsiung Hung*a and
Chittaranjan Sinhab
aInstitute of Chemistry, Academia Sinica, Nankang, Taipei – 115, Taiwan. E-mail: amitd_ju@yahoo.co.in; chhung@gate.sinica.edu.tw
bDepartment of Chemistry, Jadavpur University, Kolkata – 700032, India
cDepartament de Química Inorgànica, Facultat de Química, Universitat de Barcelona, Martí i Franquès, 1-11 08028 Barcelona, Catalunya, Spain
dDipartimento di Chimica e Farmacia, Università di Sassari, Via Vienna 2, I-07100 Sassari, Italy
eDepartament de Química, Universitat de les Illes Balears, Crta de Valldemossa km 7.5, 07122 Palma de Mallorca, Baleares, Spain. E-mail: toni.frontera@uib.es
First published on 2nd June 2016
Abstract
A rare trimetallic CuII complex, [Cu3(L)2(NO3)2] (1) has been afforded incorporating a [CuL] metalloligand, [where H2L = N,N′-bis(salicylidene)-1,3-propanediamine]. In 1, in addition to the double phenoxido bridge, the two terminal CuII atoms are linked to the central CuII by means of syn–anti bridging nitrate anions giving rise to a linear arrangement. Complex 1 exhibits strong antiferromagnetic coupling and shows an χMT value of 0.703 cm3 mol−1 K at 300 K. DFT computational studies reveal that there is a clear magneto-structural correlation between the Cu–O–Cu angle and the JCu–Cu values, which is in accordance with the experimental evidence. The biological effect of 1 on the viability of different human carcinoma cells was evaluated using MTT assay and the results indicate that this complex induces a decrease in cell-population growth of human colorectal carcinoma cells (COLO 205) with apoptosis.
Introduction
Some of the important aspects in coordination chemistry research are the rational design of organic blocking ligands and utilization of organic/inorganic bridging ligands to develop metal-organic molecules, including dinuclear systems, oligo- and polynuclear clusters, and 1-D, 2-D, and 3-D self-assemblies, having interesting properties relevant to the frontier areas such as molecular magnetism1–5 and supramolecular chemistry/crystal engineering.3a,6,7 The phenomenon of magnetic exchange in discrete molecules was discovered/explained by Guha8a and Bleaney and Bowers8b in the early 1950s while studying the variable-temperature magnetic properties of diaqua-μ1,3-acetate dicopper(II). Over the decades, the magnetic properties of coordination compounds have received tremendous attention. Eventually, a number of experimental9–11 and theoretical12–14 magneto-structural correlations were determined.Copper chemistry from a magneto-structural point of view is a very extensively studied area, both experimentally and theoretically, especially with respect to binuclear systems. However, reports on trinuclear and higher nuclearity copper compounds are rather scarce. For trinuclear species the reported data show that the triangular arrangement is more common than the linear geometry.15 Different parameters have been shown to influence the magnetic behavior of hydroxide16 or alkoxide17 bridged copper(II) complexes and from a magneto-structural point of view, linear correlations have been found between the Cu–O–Cu bridging angle (θ) and the coupling constant (J) for these compounds. A similar linear correlation between the Cu–O–Cu bridging angle (θ) and the coupling constant (J) has been proposed by Thompson et al.18 for the binuclear macrocyclic complexes bridged by a pair of phenoxide groups. For the studied complexes both phenoxo bridges coordinate the metal atoms in an equatorial–equatorial fashion and show strong antiferromagnetic exchange. However, deviation from this ideal configuration results in a large difference from the predicted value for J.19 Developing magneto-structural correlations using only experimental means is a nontrivial task because it demands structurally similar or identical complexes with all but one governing parameter being identical. Density functional theoretical (DFT) methods have been established as valuable tools in developing magneto-structural correlations and modeling the magnetic properties of the full structures of exchange-coupled systems to gain insight into the magnetic coupling mechanism and to analyze various contributions.12–14 The first and perhaps the most elegant magneto-structural correlation was determined experimentally in planar dihydroxo-bridged dicopper(II) compounds by Hatfield, Hodgson, and coworkers.10a The other types of homometallic systems concerning Cu(II) compounds for which experimental or theoretical magneto-structural correlations have been determined include alkoxo-bridged CuII4 of cubane type,10b diphenoxo-bridged CuII2,10c,d,12a monophenoxo-bridged CuII2 having axial–equatorial bridging atoms,10e linear CuII3 having a diphenoxo bridge in a pair of metal ions,10f dihalo-bridged CuII2,10e bis(μ1,1-azide) CuII2,10f bis(μ1,3-azide) CuII2,12 etc. Moreover, Le Guennic et al. have published the synthesis and X-ray characterization of an interesting CuII3 oxidase model complex that exhibits antiferromagnetic behaviour based on quasi-orthogonal molecular orbitals. In addition, Tommasino et al. have used sulfonamide-based dinuclear and 1D polymer Cu(II) complexes as antibacterial agents.20
Herein, we report the structural and magnetic interpretation of a new trinuclear CuII system, [Cu3L2(NO3)2] (1) (where H2L = N,N′-bis(salicylidene)-1,3-propanediamine).21 We also report the DFT computational carried out to provide a qualitative theoretical interpretation of the overall magnetic behavior of the complex. Such calculations allow us to propose a detailed analysis of the underlying magnetic pathways through the different bridges and also evaluate their individual contributions to the overall exchange interactions. The anticancer efficiency (in vitro) of complex 1 is investigated using various human cancer cells like, human lung carcinoma cells (A549), human colorectal carcinoma cells (COLO 205), and human hepatocellular carcinoma cells (PLC5).
Experimental
Materials
All chemicals and solvents used for the synthesis were of reagent grade, obtained commercially and used as received. Salicylaldehyde, 1,3-diaminopropane, anhydrous CuCl2 and Cu(NO3)2·3H2O were purchased from Aldrich Chemicals.Physical measurements
Microanalytical data (C, H, and N) were collected on a Perkin-Elmer 2400 CHNS/O elemental analyzer. FTIR spectra were recorded on a Perkin-Elmer RX-1 spectrophotometer in the range 4000–400 cm−1 as KBr pellets. Electronic spectra were measured on a Lambda 25 (UV-Vis-NIR) spectrophotometer. Solid state emission measurement was performed on F-4500 FL spectrophotometer using 5.0 nm slit width, scan speed of 1200 nm min−1, and PMT voltage of 700 V. EPR spectra were recorded from 0 to 8000 gauss at 77 K with an X-band (9.4 GHz) Bruker EMX spectrometer equipped with a HP 53150A microwave frequency counter. Magnetic properties were investigated with a Quantum Design MPMS-XL superconducting quantum interference device magnetometer (SQUID) at an applied field 0.5 T in a temperature range 5–300 K. The diamagnetic correction was carried out by using Pascal constants.Synthesis of the Schiff-base ligand N,N′-bis(salicylidene)-1,3-propanediamine (H2L)
The di-Schiff base ligand H2L was synthesized by standard method.20 Salicylaldehyde (1.05 mL, 10 mmol) was mixed with 1,3-propanediamine (0.42 mL, 5 mmol) in methanol (20 mL). The resulting mixture was refluxed for ca. 1.5 h and cooled. The desired yellow crystalline ligand was filtered off, washed with methanol, and dried in a vacuum desiccator containing anhydrous CaCl2.Preparation of the “metalloligand” [CuL]
A mixture of H2L (1.432 g, 5 mmol) in methanol and ammonia solution (10 mL, 20%) was added to a methanolic solution (20 mL) of anhydrous CuCl2 (0.670 g, 5 mmol) to prepare [CuL].Synthesis of [Cu3(L)2(NO3)2] (1)
To a methanolic solution (10 mL) of [CuL] (1 mmol) was added a 15 mL methanolic solution of Cu(NO3)2·3H2O (0.482 g, 2 mmol) under constant stirring. The resulting green solution was then kept boiling for 10 min and then it was allowed undisturbed at room temperature. Dark-green square-shaped single crystals of 1 were generated after one week. These were separated by filtration and air-dried before X-ray diffraction analysis. Yield: 0.62 g. Anal. calc. for C34H32Cu3N6O10: C, 46.65; H, 3.69; N, 9.60. Found: C, 46.93; H, 3.56; N, 9.39%.X-ray crystallography
The crystal structure of complex 1 was determined by X-ray diffraction methods. Intensity data and cell parameters were recorded at 100(2) K on a Bruker APEX II equipped with a CCD area detector and a graphite monochromator (MoKα radiation λ = 0.71073 Å). The raw frame data were processed using SAINT and SADABS to yield the reflection data file.22 The structure of 1 was solved by direct methods using the SIR97 program23 and refined on Fo2 by full-matrix least-squares procedures, using the SHELXL-2014/7 program24a in the WinGX suite v.2014.1.24b All non-hydrogen atoms were refined with anisotropic atomic displacements; the hydrogen atoms were included in the refinement at idealized geometry (C–H 0.95 Å) and refined “riding” on the corresponding parent atoms. The weighting scheme used in the last cycle of refinement was w = 1/[σ2Fo2 + (0.0275P)2 + 2.0803P]. Geometric calculations were performed with the PARST97 program.25 Crystal data and experimental details for data collection and structure refinement are reported in Table 1.| a Goodness-of-fit S = [Σw(Fo2 − Fc2)2/(n − p)]1/2, where n is the number of reflections and p the number of parameters.b R1 = Σ‖Fo| − |Fc‖/Σ|Fo|, wR2 = [Σ[w(Fo2 − Fc2)2]/Σ[w(Fo2)2]]1/2. | |
|---|---|
| Empirical formula | C34H32N6O10Cu3 |
| Formula weight | 875.27 |
| Temperature | 100(2) |
| Wavelength (Å) | 0.71073 |
| Crystal system | Monoclinic |
| Space group | P21/c |
| a, Å | 8.8854(4) |
| b, Å | 11.6472(5) |
| c, Å | 16.0930(6) |
| β, deg | 101.034(2) |
| Volume, Å3 | 1634.7(1) |
| Z | 2 |
| Dcalc (mg m−3) | 1.778 |
| μ (Mo Kα) (mm−1) | 2.006 |
| F(000) | 890 |
| Crystal size, mm−3 | 0.14 × 0.06 × 0.04 |
| θ range for data collection | 2.17–27.10 |
| Reflections collected/unique | 56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 645/3619 [R(int) = 0.0963] 645/3619 [R(int) = 0.0963] |
| Observed reflections [Fo > 4σ(Fo)] | 2990 |
| Data/restraints/parameters | 3619/0/242 |
| Final R indices [Fo > 4σ(Fo)]b | R1 = 0.0309, wR2 = 0.0669 |
| R indices (all data) | R1 = 0.0435, wR2 = 0.0726 |
| Goodness-of-fit on F2a | 1.002 |
| Largest diff. peak and hole, e Å−3 | 0.393 and −0.418 |
Theoretical calculation
For the study of the magnetic properties of the complexes, the calculations have been carried out using density functional theory (DFT) combined with the broken symmetry approach26 by means of GAUSSIAN 09 package.27 The level of theory used in this study is B3LYP/6-31+G* which is a good compromise between the size of the system and the computational demands. For these calculations we have used the crystallographic coordinates where the positions of the H atoms have been optimized.For linear trinuclear system Cu1–Cu2–Cu3, the spin Hamiltonian describing the low-lying states in zero field may be written as H = −J(S1S2 + S2S3) − J′S1S3 where J and J′ denote the exchange coupling constant between nearest-neighbour and terminal centers, respectively. The three possible spin levels |S = S1 + S2 + S3, S′ = S1 + S3〉 for three centers are: one quartet |3/2,1〉 (Q) and two doublets |1/2,1〉 and |1/2,0〉 (D1 and D2), respectively. Since we are dealing with a strictly symmetric system in which a symmetry element relates two of the magnetic centers (1 and 3) and passes across the third one (2), we can safely state that J12 = J23 = J with a concomitant simplification of the calculations. Moreover, the interaction between Cu1 and Cu3 (denoted as Cu1′ in this manuscript) can be neglected considering the separation of the two terminal copper(II) metal centers. Therefore, the magnetic coupling constant for a Cu(II) trinuclear system with a negligible interaction between the terminal copper(II) ions can be obtained using the energy of only two states. However, we have computed the energies of the quartet and all doublets using the BS approach to compute the Js. These calculations allow us to corroborate that J12 = J23 and that J13 ≈ 0. We have further corroborated that J13 = 0 by performing calculations in a model where the central Cu atom has been substituted by Zn, as proposed by Alvarez group.28 The resulting complex can be treated as a dinuclear Cu system. Both the triplet and singlet states of this model CuZnCu system are isoenergetic, thus confirming that the interaction between the terminal Cu atoms is negligible. It should be mentioned that the widely and successfully used29 broken-symmetry DFT approach, also used herein, is not a unique methodology to compute and interpret the magnetic properties in quantum chemistry. For instance, ab initio methods based on difference dedicated configuration interaction30 (e.g., CASSCF/DDCI) give excellent results and offer the possibility to finely analyse the mechanisms and origin of the magnetic properties, taking advantage of access to the wave function of all spin states of interest. However, this methodology was not used for the system studied herein for computational reasons (the complex has 85 atoms) and, moreover, a good agreement with experiment has been found using the broken symmetry approach. Illas' group31 have recently compared the performance of both methodologies (spin adapted versus broken symmetry approaches)31a and also treated the problem of dealing with magnetic coupling in trinuclear Cu(II) complexes.31b The calculation of the EPR g-tensor has been performed using Gaussian-09 program27 and the B3LYP/EPR-III level of theory for all atoms apart from the Cu atom, where we have used the 6-311+G* basis set.
Cell culture
Human lung carcinoma cells (A549 cells), human colorectal carcinoma cells (COLO 205 cells) and human hepatocellular carcinoma cells (PLC5 cells) were obtained from the American Type Culture Collection (ATCC, Bethesda, MD, USA). A549 cells were grown in a medium consisting of 90% RPMI 1640 with 10% fetal bovine serum supplemented with 0.1 mM nonessential amino acid, 2 mM L-glutamine, 1 mM sodium pyruvate and 100 U mL−1 penicillin–streptomycin. COLO 205 cells and HT-29 cells were grown in 90% RPMI 1640 medium supplemented with 10% fetal bovine serum, 100 units per mL penicillin, and 100 μg mL−1 streptomycin. PLC5 cells were grown in 90% Dulbecco's modified Eagle's medium, supplemented with 10% fetal bovine serum, 2 mM L-glutamine, 1.5 g L−1 sodium bicarbonate, 0.1 mM non-essential amino acids, 1.0 mM sodium pyruvate, 100 units per mL penicillin and 100 μg mL−1 streptomycin. Human cancer cells were cultured at 37 °C in a humidified 5% CO2 incubator.Cell viability by MTT assay
The MTT [3-(4,5-dimethylthiazol-2-yl)-2,5-diphenyl tetrazolium bromide] (Sigma Chemical Co., St. Louis, MO, USA) assay was performed according to the method of Mosmann.32 Human colorectal carcinoma cells were plated into 96-well microtiter plates at a density of 1 × 104 cells per well. After 24 h, the culture medium was replaced by 200 μL (0–50 μM) of the compound, and the cells were incubated for 24 and 48 h. The final concentration of the solvent was less than 0.1% in cell culture medium. The culture medium was removed and replaced by 90 μL fresh culture medium. Ten microliters of sterile filtered MTT solution (5 mg mL−1) in phosphate buffered saline (PBS, pH = 7.4) was added to each well, thereby reaching a final concentration of 0.5 mg MTT per mL. After 5 h, the unreacted dye was removed, and the insoluble formazan crystals were dissolved in 200 μL per well DMSO and measured spectrophotometrically in a VersaMax tunable microplate reader (Molecular Devices, Sunnyvale, CA, USA) at 570 nm. The relative cell viability (%) related to control wells containing cell culture medium without samples was calculated by A570 nm[sample]/A570 nm[control] × 100.Results and discussion
Synthesis, IR and electronic spectra
The compartmental Schiff base precursor, H2L, was acquired from the condensation of salicylaldehyde and 1,3-diaminopropane. This ligand displays a distinct coordination pocket which can encapsulate CuII center. The large size of the inner compartment, formed by the N2O2 donor set, is particularly appropriate to accommodate another sizable 3d ion. The stoichiometric reaction of metalloligand [CuL] and Cu(NO3)2·3H2O in MeOH yielded the trinuclear species shown in Scheme 1.The infrared spectra of complex 1 is consistent with the structural data presented in this paper. The IR spectra shows a strong and sharp band at 1634 cm−1 for the azomethine νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N group in 1.33 The phenolic νAr–O stretching frequency is present at 1283 cm−1.34 Complex 1 shows strong bands at 1385 cm−1, ascribable to the stretching frequency of NO3− as coordinated ligand.33 These assignments have been corroborated using DFT calculations (B3LYP/6-31+G* level of theory) that predict 1657 cm−1 for the azomethine group and 1263 cm−1 for the phenolic stretching. In case of the NO3− coordinated ligand, the DFT calculations show two bands located at 1409 and 1355 cm−1.
N group in 1.33 The phenolic νAr–O stretching frequency is present at 1283 cm−1.34 Complex 1 shows strong bands at 1385 cm−1, ascribable to the stretching frequency of NO3− as coordinated ligand.33 These assignments have been corroborated using DFT calculations (B3LYP/6-31+G* level of theory) that predict 1657 cm−1 for the azomethine group and 1263 cm−1 for the phenolic stretching. In case of the NO3− coordinated ligand, the DFT calculations show two bands located at 1409 and 1355 cm−1.
Structural analysis
X-ray diffraction analysis on single crystals reveals that the resulting complex is the trinuclear unit [Cu3L2(NO3)2] (1). Crystallographic and refinement parameters are summarized in Table 1. The molecular structure of [Cu3L2(NO3)2] (1) is shown in Fig. 1; selected bond distances and angles are listed in Table 2. The trimeric complex consists of two symmetry-related moieties, comprising three copper ions, two Schiff-base ligands and two nitrate ions. The central copper ion Cu2 lies on an inversion center, and coordinates six oxygen atoms in an octahedral geometry, with O4 and O4′ from the nitrate ion in the axial positions, and the four phenoxide oxygens O1, O2, O1′ and O2′ in the equatorial plane. The external copper centers Cu1 and Cu1′ are penta-coordinated in a square-pyramidal fashion (as indicated by the Addison parameter (τ = 0.067); τ = 0 for an ideal square pyramid and τ = 1 for a trigonalbipyramid35), with the apical position occupied by the acetate oxygen O3 and O3′, respectively and the equatorial plane formed by two nitrogen atoms of the Schiff base (N1, N2 or N1′ and N2′) and the two oxygen atoms O1 and O2 (O1′ and O2′) from the phenoxide moiety, which bridge the external copper centers with the central one. The ligand deviates significantly from planarity, presenting an overall concave geometry, with the aromatic “wings” pointing away from the bridging acetate. Distances and angles are in the usual range for complex 1 (see Table 2).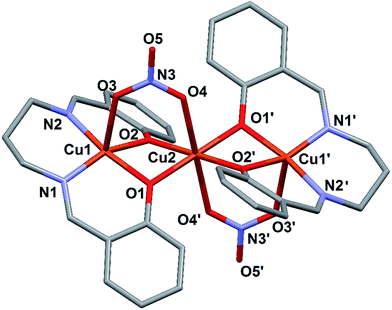 | ||
| Fig. 1 Molecular structure of 1 with partial labelling scheme. Hydrogen atoms have been omitted for clarity. The symmetry operations for generating equivalent atoms are: −x, −y, −z. | ||
| Cu1–N1 | 1.961(1) | Cu2–O2 | 1.963(2) |
| Cu1–N2 | 1.950(2) | Cu2–O4 | 2.395(2) |
| Cu1–O1 | 1.954(2) | Cu1⋯Cu2 | 2.951(1) |
| Cu1–O2 | 1.942(2) | O1–Cu1–N2 | 169.92(8) |
| Cu1–O3 | 2.324(2) | O2–Cu1–N1 | 160.88(8) |
| Cu2–O1 | 1.974(2) | O1–Cu2–O2 | 77.80(7) |
The Cu⋯Cu distance is 2.951 Å and the two Cu–O–Cu bridging angles are 97.43° and 98.14°. The shortest inter-chain Cu⋯Cu separation corresponds to 9.933 Å between Cu2 ions (see Fig. 2).
Emission spectra
At room temperature, complex 1 shows a strong blue luminescence with emission maxima appearing around 290 nm and 395 nm, upon excitation at 250 nm in solid state (see Fig. 3). Comparable emissions come from the free H2L ligand, observed around the same wavelengths; thus the luminescent behavior of the complex can be rationalized as intra ligand n–π* and π–π* charge transfer transitions. An additional weak hump is observed for the complex around 555 nm (inset in Fig. 3) corresponding to the metal-to-ligand charge transfer where the electrons are transferred from the Cu-3d to O-2p and N-2p states.36 | ||
| Fig. 3 Solid state emission spectra of complex 1, measured at room temperature. Inset shows a weak hump appearing around 555 nm. | ||
EPR spectra
The EPR spectrum, recorded at 77 K on a polycrystalline powder of complex 1, is reported in Fig. 4. The magnetic range explored was 0–8000 gauss, but only the region where the transitions were detected is shown (see also Fig. 5). It is characterised by a very broad and unresolved resonance, due to the exchange coupling between the neighbouring copper ions. The isotropic value of g(giso) is 2.165. An analogous behaviour is shown by other trinuclear Cu(II) species formed by Schiff bases.37 | ||
| Fig. 4 X-band EPR spectra of 1 recorded at 77 K: (a) the solid polycrystalline powder and (b) the polycrystalline powder dissolved in a mixture CH2Cl2/toluene 60/40 v/v. | ||
 | ||
| Fig. 5 Anisotropic X-band EPR spectra recorded at 77 K on the polycrystalline powder of complex 1 dissolved in (a) DMF and (b) DMSO. | ||
Complex 1 was dissolved in two types of solvents: two coordinating solvents such as DMF (Fig. 5, trace a) and DMSO (Fig. 5, trace b) and one non-coordinating mixture such as CH2Cl2/toluene 60/40 v/v (Fig. 4, trace b). The results are very different. In the mixture CH2Cl2/toluene 60/40 v/v (Fig. 4, trace b) the EPR spectrum of complex 1 overlaps perfectly with that recorded on the solid compound, indicating that the structure is retained in these solvents. No hyperfine coupling between the unpaired electron and the 63,65Cu nucleus is revealed. EPR spectra in DMF and DMSO (Fig. 5, trace a and b) are typical of mononuclear Cu(II) species with an axial symmetry. The order gz > gx ∼ gy is consistent with a species with an axial symmetry and the unpaired electron on a molecular orbital (MO) with main contribution from the Cu dx2−y2 atomic orbital.38,39
Magnetic properties
Magnetic measurements were carried out on polycrystalline powder samples where the compound shows a strong antiferromagnetic behaviour. The magnetic behaviour plot of complex 1 in the form of χMT vs. T and M/NμB vs. H at 2 K are represented in Fig. 6 and 7. The compound shows a χMT value of 0.703 cm3 mol−1 K at 300 K, which is a smaller value than the expected for three uncoupled S = 1/2 ions with g = 2.0 (1.125 cm3 mol−1 K). With cooling temperature, χMT decreases dramatically, reaching a plateau from ca. 75 K, with χMT close to 0.43 cm3 mol−1 K, corresponding to an isolated S = 1/2 with g = 2.14. This behaviour indicates a strong antiferromagnetic interaction. Below this temperature, χMT remains constant (0.427 cm3 mol−1 K at 2 K). | ||
| Fig. 6 Plot of observed χMT vs. T of complex 1. The solid line represents the best theoretical fit of χMT vs. T. | ||
 | ||
| Fig. 7 Plot of observed χMT vs. T and M/NμB vs. H at 2 K of 1. The solid line represents the simulation of M/NμB at 2 K with S = 1/2 and g = 2.14. | ||
The magnetization measurements at 2 K up to an external field of 5 T shows the saturation of the complex 1 tending to 1.01NμB (one electron) for trinuclear Cu(II) unit (Fig. 7). The analysis of the experimental magnetic data was performed using the simplified Van Vleck equation for linear system with three S = 1/2 ions (eqn (1)), where N is Avogadro's number, μB is the Bohr magneton, kB is the Boltzmann constant.
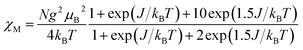 | (1) |
| H = −J(S1S2 + S2S1′) |
The best fit parameters obtained where J = −306.8 cm−1 and g = 2.15 with R = 6.05 × 10−6  .
.
DFT study
The theoretical study is devoted to the rationalization of the magnetic results (EPR and ferromagnetic coupling). For the EPR analysis, we have optimized the mononuclear complex proposed above and we have represented the singly occupied molecular orbital (SOMO) using DFT calculation (B3LYP/6-31+G*). The main contribution comes from Cu dx2−y2 atomic orbital with a minor participation of the atomic orbitals of the N, N, O, O donors directly bonded to copper (see Fig. S4†). Moreover the calculated g values (gcalcd) are also in reasonable agreement with the experimental ones (vide supra) and the axial symmetry of the mononuclear complex (gcalcdz = 2.222, gcalcdy = 2.070, gcalcdx = 2.063, i.e. gcalcdz > gcalcdx ∼ gcalcdy). These features suggest that the chemical bridges in 1 are broken and mononuclear 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 species with composition [Cu(salpn)] (S = 1/2) are formed in DMF and DMSO. This transformation has been observed for other polynuclear Cu(II) complexes,40 and in particular for trinuclear Cu(II) species.37 The spin Hamiltonian parameters are: gz = 2.245 and Az = 181.3 × 10−4 cm−1 (DMF) and gz = 2.248 and Az = 180.2 × 10−4 cm−1 (DMSO). These values can be attributed to the (Ophenolate, Nimine, Nimine, Ophenolate) donor set of salpn. The slight decrease of the value of Az compared with Cu–salpn derivatives species (184–193 × 10−4 cm−1)37,41 could suggest the weak coordination of a nitrate ion in the axial position.
1 species with composition [Cu(salpn)] (S = 1/2) are formed in DMF and DMSO. This transformation has been observed for other polynuclear Cu(II) complexes,40 and in particular for trinuclear Cu(II) species.37 The spin Hamiltonian parameters are: gz = 2.245 and Az = 181.3 × 10−4 cm−1 (DMF) and gz = 2.248 and Az = 180.2 × 10−4 cm−1 (DMSO). These values can be attributed to the (Ophenolate, Nimine, Nimine, Ophenolate) donor set of salpn. The slight decrease of the value of Az compared with Cu–salpn derivatives species (184–193 × 10−4 cm−1)37,41 could suggest the weak coordination of a nitrate ion in the axial position.
The determination of the J values was carried out using DFT calculations combined with the broken symmetry approach. The magnetic coupling constant J of the system is described by the isotropic Hamiltonian described above. For completeness, we have computed all possible spin states (see computational methods, and Table S1†) and corroborated that the exchange integral between the neighbouring Cu(II) ions are identical (J1–2 = J1′–2 = J) and that J1–3 is zero. As shown by Illas et al.,29 in the case of strictly symmetric systems (e.g. complex 1) in which a symmetry element relates two of the magnetic centers (1 and 1′) and passes across the third one (2), it can be safely stated that J1–2 = J1′–2 = J with a concomitant simplification of the spectrum arising from the corresponding Heisenberg. If the antiferromagnetic D1 ground state (as in complex 1) energy is arbitrarily set to zero, the energy of the other doublet D2 is −J and that of Q is −3J/2.
The theoretical calculation of the J value has been performed using the crystallographic coordinates and we have obtained a theoretical J value of −356.4 cm−1 at the B3LYP/6-31+G* level of theory, which is in reasonable agreement with the experimental value (−306.8 cm−1) and confirms the antiferromagnetic coupling. In order to further examine the magnetic coupling mechanism, the spin density distribution has been analysed. The atomic spin density population values of the Cu metal centers and the atoms of the ligands directly bonded to them are summarized in Table S2.† The Mulliken spin population analysis for the HS configuration indicates that a significant spin (ca. 1.04 e) is delocalized through the ligands, and the rest (1.96 e) is carried by the Cu atoms. The representation of the spin distributions corresponding to doublet (the spin density of one of the “broken-symmetry” wavefunction) and quadruplet ground spin states for complex 1 are plotted in Fig. 8, where positive (blue) and negative (green) signs denote α and β spin states, respectively and the magnetic orbitals for the broken symmetry state are represented in Fig. S5.† The broken-symmetry spin densities on the Cu1/Cu1′ and Cu2 ions have similar absolute values but opposite signs. The spin population values (+0.60 on Cu1 and −0.73 on Cu2) reveal that they are the magnetic centres and that the spin delocalization is strong enough that ∼35% of the spin for the unpaired electrons on the Cu(II) centres is delocalized to the ligand atoms. The spin population on the ligand atoms have the same signs as that of the Cu(II) atoms to which they are bonded (see Table S2†). Remarkably, the spin carried by the phenoxido oxygen atoms is ca. 0.13 e in the high-spin state and ±0.02 e in the broken-symmetry state of complex 1. In contrast the spin density is negligible on the bridging nitrato ligands. Consequently only the bridging O atoms mediate the magnetic exchange.
 | ||
| Fig. 8 Graphical representation of spin density (contour 0.004 e Å−3) at the high spin (A) and low spin (B) configurations of complex 1. | ||
In octahedral Cu(II) complexes, each dx2−y2 orbital contains an unpaired electron and this orbital of the metal atom along with the local orbitals of the bridging ligands are involved in the super-exchange pathway. The Cu–Cu separation in 1 is large (2.951 Å), indicating that no direct exchange mechanism is likely to contribute to the magnetic coupling. The strong antiferromagnetic coupling in 1 is ascribed solely to super-exchange mechanism within the central-terminal copper pairs and it is efficiently mediated by the phenoxido atoms, as confirmed by the spin density plot. From the shape of the spin density surface, it is evident the participation of the dx2−y2 orbitals of Cu(II) metal centers and the px orbital of the oxygen thus confirming that the bridging O atoms are effective for mediating the magnetic exchange in agreement with the low spin atomic population at the O atom in the broken-symmetry state of 1 (see Table S2†).
Finally, the strong and antiferromagnetic coupling observed in compound 1 through the double phenoxido bridges can be explained in terms of magneto-structural correlations established for phenoxido bridges18 where the Cu–O–Cu bond angle (α) and the dihedral angle in the Cu2O2 entity are prominent players. In fact, for double phenoxido bridged Cu(II) complexes, there exists a linear correlation between the Cu–O–Cu bond angle and the coupling constant (2J (cm−1) = −31.95α + 2462).18 This linear correlation works quite well in compound 1 and yields an antiferromagnetic exchange coupling of −324.9 cm−1 for the Cu1–Cu2 exchange coupling, slightly above (in absolute value) the experimental value of −306.8 cm−1.
Effects of the complexes on the cell population growth in human cancer cells
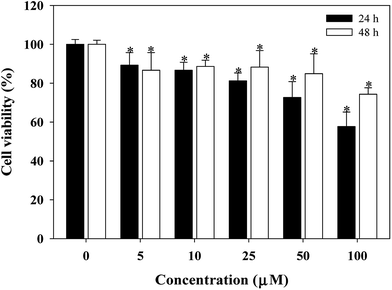
An uncontrolled cell proliferation is perceived in many human diseases including cancer. The potential anticancer activities of complex 1 are analyzed using a model system for the in vitro control of tumor-cell proliferation. Fig. 9, 10 and 11 show the effects of complex 1 on the cell population growth in human cancer cells [including human lung carcinoma cells (A549 cells), human colorectal carcinoma cells (COLO 205 cells), and human hepatocellular carcinoma cells (PLC5 cells)]. To assess the inhibitory effect on the growth of human cancer cells, the cells were cultured for 24 and 48 h with or without the test compound (0–100 μM), and the population growth was determined by the MTT assay. Complex 1 presents the strongest population growth inhibition of human colorectal carcinoma cells (COLO 205 cells) (Fig. 10). Moreover, the 50% inhibitory concentration (IC50) as determined by MTT assay after 48 h of incubation showed the highest activity with an IC50 value of 46.00 ± 1.09 μM. Complex 1 could be further tested by an in vivo model to justify if it is effective for prevention of human cancer.Conclusions
In conclusion, the reaction of a “metalloligand” [CuL] with copper(II) nitrate affords a doubly nitrato- and phenoxido-bridged trinuclear Cu(II) derivative. The EPR measurements show that the trinuclear structure is maintained in non-coordinating solvents, whereas mononuclear Cu(II) species are formed in coordinating solvents such as DMF and DMSO. In DMF a well-resolved hyperfine structure is observed, due to the coupling between the unpaired electron and the 63,65Cu nucleus. Variable temperature magnetic susceptibility reveals that there exists a strong antiferromagnetic coupling among the trinuclear copper derivatives. For the title homometallic complex theoretical calculation supports the experimentally observed fact that it has a large tendency to show antiferromagnetic coupling. Various human cancer cells are used to investigate the anticancer activity in vitro using the copper(II) complex. Future investigations will focus on other transition metal ions with different tetradentate Schiff base precursors and studies on single molecular magnetism and chemo-sensor activities for selective detection of metal ions are currently being carried out in our laboratories.Acknowledgements
AD and CHH express their appreciation to the Ministry of Science and Technology, Taiwan for financial assistance. KD would like to thank DST (Department of Science and Technology, New Delhi, India) for the grant (SR/S1/IC-31/2008) to carry out the present study. We also wish to thank Dr Chiara Massera for her valuable suggestions regarding crystallography. AF and AB thank MINECO of Spain (projects CTQ2014-57393-C2-1-P and CONSOLIDER INGENIO CSD2010-00065, FEDER funds) for funding. We also thank the CTI (UIB) for computational facilities.References
- (a) O. Kahn, Molecular Magnetism, VCH Publications, New York, 1993 Search PubMed; (b) Single-Molecule Magnets and Related Phenomena, ed. R. Winpenny, Springer, New York, 2006 Search PubMed; (c) Magnetism: Molecules to Materials II, ed. J. S. Miller and M. Drillon, Willey-VCH, Weinheim, Germany, 2001 Search PubMed.
- (a) C. Papatriantafyllopoulou, T. C. Stamatatos, W. Wernsdorfer, S. J. Teat, A. J. Tasiopoulos, A. Escuer and S. P. Perlepes, Inorg. Chem., 2010, 49, 10486–10496 CrossRef CAS PubMed; (b) P. Albores and E. Rentschler, Angew. Chem., Int. Ed., 2009, 48, 9366–9370 CrossRef CAS PubMed.
- (a) S. Sasmal, S. Hazra, P. Kundu, S. Majumder, N. Aliaga-Alcalde, E. Ruiz and S. Mohanta, Inorg. Chem., 2010, 49, 9517–9526 CrossRef CAS PubMed; (b) R. Koner, S. Hazra, M. Fleck, A. Jana, C. R. Lucas and S. Mohanta, Eur. J. Inorg. Chem., 2009, 4982–4988 CrossRef CAS; (c) H.-L. Sun, Z.-M. Wang and S. Gao, Chem.–Eur. J., 2009, 15, 1757–1764 CrossRef CAS PubMed; (d) G. Manca, J. Cano and E. Ruiz, Inorg. Chem., 2009, 48, 3139–3144 CrossRef CAS PubMed; (e) Z. E. Serna, R. Cortes, M. K. Urtiaga, M. G. Barandika, L. Lezama, M. I. Arriortua and T. Rojo, Eur. J. Inorg. Chem., 2001, 865–872 CrossRef CAS.
- (a) O. Kahn and T. Mallah, J. Chem. Soc., Dalton Trans., 1989, 1117–1126 RSC; (b) P. Cheng, D. Liao, S. Yan, Z. Jiang, G. Wang, X. Yao and H. Wang, Inorg. Chim. Acta, 1996, 248, 135–137 CrossRef CAS; (c) A. Benzekri, P. Dubourdeaux, J.-M. Latour, J. Laugier and P. Rey, Inorg. Chem., 1988, 27, 3710–3716 CrossRef CAS.
- (a) T. Mallah, O. Kahn, J. Gouteron, S. Jeannin, Y. Jeannin and C. J. O'Connor, Inorg. Chem., 1987, 26, 1375–1380 CrossRef CAS; (b) A. Banerjee, R. Singh, E. Colacio and K. K. Rajak, Eur. J. Inorg. Chem., 2009, 277–284 CrossRef CAS; (c) M.-L. Boillot, O. Kahn, C. J. O'Connor, J. Gouteron, S. Jeannin and Y. Jeannin, J. Chem. Soc., Chem. Commun., 1985, 178–180 RSC.
- (a) Transition Metals in Supramolecular Chemistry, in Perspectives in Supramolecular Chemistry 5, ed. J.-P. Sauvage, Wiley, London, 1999 Search PubMed; (b) M. J. Zaworotko, J. Am. Chem. Soc., 2010, 132, 7821–7822 CrossRef CAS; (c) J. J. Zhang, L. Wojtas, R. W. Larsen, M. Eddaoudi and M. J. Zaworotko, J. Am. Chem. Soc., 2009, 131, 17040–17041 CrossRef CAS PubMed.
- (a) M. Nayak, R. Koner, H.-H. Lin, U. Florke, H.-H. Wei and S. Mohanta, Inorg. Chem., 2006, 45, 10764–10773 CrossRef CAS PubMed; (b) M. Nayak, A. Jana, M. Fleck, S. Hazra and S. Mohanta, CrystEngComm, 2010, 12, 1416–1421 RSC.
- (a) B. Guha, Proc. R. Soc. London, 1951, 206, 353 CrossRef CAS; (b) B. Bleaney and K. D. Bowers, Proc. R. Soc. London, 1952, 214, 451 CrossRef CAS.
- (a) O. Kahn, Molecular Magnetism, VCH, New York, 1993 Search PubMed; (b) Magneto-Structural Correlations in Exchange Coupled Systems, ed. R. D. Willet, D. Gatteschi and O. Kahn, Reidel, Dordrecht, The Netherlands, 1985 Search PubMed.
- (a) V. M. Crawford, H. W. Richardson, J. R. Wasson, D. J. Hodgson and W. E. Hatfield, Inorg. Chem., 1976, 15, 2107–2110 CrossRef CAS; (b) L. Merz and W. Haase, J. Chem. Soc., Dalton Trans., 1980, 875–879 RSC; (c) L. K. Thompson, S. K. Mandal, S. S. Tandon, J. N. Bridson and M. K. Park, Inorg. Chem., 1996, 35, 3117–3125 CrossRef CAS PubMed; (d) O. Wichmann, H. Sopo, E. Colacio, A. J. Mota and R. Sillanpaä, Eur. J. Inorg. Chem., 2009, 4877–4886 CrossRef CAS; (e) S. Laborda, R. Clerac, C. E. Anson and A. K. Powell, Inorg. Chem., 2004, 43, 5931–5943 CrossRef CAS PubMed; (f) L. Botana, J. Ruiz, J. M. Seco, A. J. Mota, A. Rodrıguez-Dieguez, R. Sillanpaä and E. Colacio, Dalton Trans., 2011, 40, 12462–12471 RSC; (g) B. Le Guennic, S. Petit, G. Chastanet, G. Pilet, D. Luneau, N. Ben Amor and V. Robert, Inorg. Chem., 2008, 47, 572–577 CrossRef CAS PubMed.
- (a) K. K. Nanda, L. K. Thompson, J. N. Bridson and K. Nag, J. Chem. Soc., Chem. Commun., 1994, 1337–1338 RSC; (b) M. A. Palacios, A. J. Mota, J. E. Perea-Buceta, F. J. White, E. K. Brechin and E. Colacio, Inorg. Chem., 2010, 49, 10156–10165 CrossRef CAS PubMed; (c) S. Sasmal, S. Hazra, P. Kundu, S. Dutta, G. Rajaraman, E. C. Sañudo and S. Mohanta, Inorg. Chem., 2011, 50, 7257–7267 CrossRef CAS PubMed.
- (a) D. Venegas-Yazigi, D. Aravena, E. Spodine, E. Ruiz and S. Alvarez, Coord. Chem. Rev., 2010, 254, 2086–2095 CrossRef CAS; (b) M. F. Charlot, O. Kahn, S. Jeannin and Y. Jeannin, Inorg. Chem., 1980, 19, 1410–1411 CrossRef CAS; (c) E. Ruiz, P. Alemany, S. Alvarez and J. Cano, J. Am. Chem. Soc., 1997, 119, 1297–1303 CrossRef CAS; (d) A. Rodrıguez-Fortea, P. Alemany, S. Alvarez and E. Ruiz, Inorg. Chem., 2002, 41, 3769–3778 CrossRef; (e) E. Ruiz, J. Cano, S. Alvarez and P. Alemany, J. Am. Chem. Soc., 1998, 120, 11122–11129 CrossRef CAS; (f) E. Ruiz, C. de Graaf, P. Alemany and S. Alvarez, J. Phys. Chem. A, 2002, 106, 4938–4941 CrossRef CAS.
- G. Manca, J. Cano and E. Ruiz, Inorg. Chem., 2009, 48, 3139–3144 CrossRef CAS PubMed.
- (a) G. Rajaraman, F. Totti, A. Bencini, A. Caneschi, R. Sessoli and D. Gatteschi, Dalton Trans., 2009, 3153–3161 RSC; (b) S. K. Singh, N. K. Tibrewal and G. Rajaraman, Dalton Trans., 2011, 40, 10897–10906 RSC; (c) T. Rajeshkumar and G. Rajaraman, Chem. Commun., 2012, 48, 7856–7858 RSC.
- A. Roth, J. Becher, C. Herrmann, H. Gorls, G. Vaughan, M. Reiher, D. Klemm and W. Plass, Inorg. Chem., 2006, 45, 10066–10076 CrossRef CAS PubMed.
- V. H. Crawford, H. W. Richardson, J. R. Wasson, D. J. Hodgson and W. E. Hatfield, Inorg. Chem., 1976, 15, 2107–2110 CrossRef CAS.
- (a) L. Merz and W. Haase, J. Chem. Soc., Dalton Trans., 1980, 875–879 RSC; (b) M. Handa, N. Koga and S. Kida, Bull. Chem. Soc. Jpn., 1988, 61, 3853–3857 CrossRef CAS.
- L. K. Thompson, S. K. Mandal, S. S. Tandon, J. N. Bridson and M. K. Park, Inorg. Chem., 1996, 35, 3117–3125 CrossRef CAS PubMed.
- Y.-S. Xie, X.-T. Liu, J. Ni and Q.-L. Liu, J. Mol. Struct., 2003, 655, 279–284 CrossRef CAS.
- (a) J.-B. Tommasino, G. Pilet, F. N. R. Renaud, G. Novitchia, V. Robert and D. Luneau, Polyhedron, 2012, 37, 27–34 CrossRef CAS; (b) J.-B. Tommasino, G. Chastanet, B. Le Guennic, V. Robert and G. Pilet, New J. Chem., 2012, 36, 2228–2235 RSC.
- J. Reglinski, S. Morris and D. E. Stevenson, Polyhedron, 2002, 21, 2167–2174 CrossRef CAS.
- (a) SADABS, Bruker AXS, Madison, Wisconsin, USA, 2004 Search PubMed; (b) SAINT, Software Users Guide, Version 6.0, Bruker Analytical X-ray Systems, Madison, WI, 1999 Search PubMed; (c) G. M. Sheldrick, SADABS v2.03: Area-Detector Absorption Correction. University of Göttingen, Germany, 1999 Search PubMed.
- A. Altomare, M. C. Burla, M. Camalli, G. L. Cascarano, C. Giacovazzo, A. Guagliardi, A. G. G. Moliterni, G. Polidori and R. Spagna, J. Appl. Crystallogr., 1999, 32, 115–119 CrossRef CAS.
- (a) G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed; (b) L. J. Farrugia, J. Appl. Crystallogr., 1999, 32, 837–838 CrossRef CAS.
- M. Nardelli, J. Appl. Crystallogr., 1996, 29, 296–300 CrossRef CAS.
- (a) L. J. Noodleman, J. Chem. Phys., 1981, 74, 5737–5743 CrossRef CAS; (b) L. Noodleman and E. R. Davidson, Chem. Phys., 1986, 109, 131–143 CrossRef; (c) L. Noodleman, C. Y. Peng, D. A. Case and J. M. Mouesca, Coord. Chem. Rev., 1995, 144, 199–244 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, M. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc, Wallingford CT, 2009.
- Q. Zhongnan, W. Jian, L. Chengbu, W. Ruoxi and S. Youmin, Chin. Sci. Bull., 2006, 51, 1421–1425 Search PubMed.
- (a) N. Onofrio and J.-M. Mouesca, Inorg. Chem., 2011, 50, 5577–5586 CrossRef CAS PubMed; (b) F. Neese, Coord. Chem. Rev., 2009, 253, 526–563 CrossRef CAS; (c) F. Neese, T. Petrenko, D. Ganyushin and G. Olbrich, Coord. Chem. Rev., 2007, 251, 288–327 CrossRef CAS; (d) C. Adamo, V. Barone, A. Bencini, R. Broer, M. Filatov, N. M. Harrison, F. Illas and J.-P. Malrieu, J. Chem. Phys., 2006, 124, 101–107 CrossRef PubMed; (e) C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158 CrossRef CAS; (f) C. Adamo, A. di Matteo and V. Barone, Adv. Quantum Chem., 2000, 36, 45 CrossRef.
- J. Miralles, O. Castell, R. Caballol and J. P. Malrieu, Chem. Phys., 1993, 172, 33–43 CrossRef CAS.
- (a) R. Costa, R. Valero, D. R. Mañeru, I. de P. R. Moreira and F. Illas, J. Chem. Theory Comput., 2015, 11, 1006–1019 CrossRef CAS PubMed; (b) D. R. Mañeru, R. Costa, M. G. Márquez, I. de P. R. Moreira and F. Illas, J. Chem. Theory Comput., 2015, 11, 3650–3660 CrossRef PubMed.
- T. Mosmann, J. Immunol. Methods, 1983, 65, 55–63 CrossRef CAS PubMed.
- K. Nakamoto, Infrared and Raman Spectra of Inorganic and Coordination Compounds, Parts A and B, John Wiley, New York, 5th edn, 1997 Search PubMed.
- C. T. Yang, B. Moubaraki, K. S. Murray, J. D. Ranford and J. J. Vittal, Inorg. Chem., 2001, 40, 5934–5941 CrossRef CAS PubMed.
- A. W. Addison, T. N. Rao, J. Reedijk, J. van Rijn and G. C. Verschoor, J. Chem. Soc., Dalton Trans., 1984, 1349–1356 RSC.
- B. Chen and G. Qian, “Metal–Organic Frameworks for Photonic Applications”, Springer, Heidelberg, 2014 Search PubMed.
- (a) S. Thakurta, J. Chakraborty, G. Rosair, J. Tercero, M. S. El Fallah, E. Garribba and S. Mitra, Inorg. Chem., 2008, 47, 6227–6235 CrossRef CAS PubMed; (b) S. Thakurta, C. Rizzoli, R. J. Butcher, C. J. Gómez-García, E. Garribba and S. Mitra, Inorg. Chim. Acta, 2010, 363, 1395–1403 CrossRef CAS; (c) S. Saha, A. Sasmal, C. R. Choudhury, C. J. Gomez-Garcia, E. Garribba and S. Mitra, Polyhedron, 2014, 69, 262–269 CrossRef CAS.
- (a) B. J. Hathaway and D. E. Billing, Coord. Chem. Rev., 1970, 5, 143–207 CrossRef CAS; (b) B. J. Hathaway, Struct. Bonding, 1984, 57, 55–118 CrossRef CAS.
- E. Garribba and G. Micera, J. Chem. Educ., 2006, 83, 1229–1235 CrossRef CAS.
- (a) J. C. Jeffery, J. P. Maher, C. A. Otter, P. Thornton and M. D. Ward, J. Chem. Soc., Dalton Trans., 1995, 819–824 RSC; (b) G. van Albada, I. Mutikainen, W. J. J. Smeets, A. L. Spek, U. Turpeinen and J. Reedijk, Inorg. Chim. Acta, 2002, 327, 134–139 CrossRef CAS; (c) W. A. Alves, R. H. de Almeida Santos, A. Paduan-Filho, C. C. Becerra, A. C. Borin and A. C. A. M. da Costa Ferriera, Inorg. Chim. Acta, 2004, 357, 2269–2278 CrossRef CAS; (d) M. A. Ali, A. H. Mirza, R. J. Fereday, R. J. Butcher, J. M. Fuller, S. C. Drew, L. R. Gahan, G. R. Hanson, B. Moubaraki and K. S. Murray, Inorg. Chim. Acta, 2005, 358, 3937–3948 CrossRef CAS; (e) I. A. Koval, M. Sgobba, M. Huisman, M. Lüken, E. Saint-Aman, P. Gamez, B. Krebs and J. Reedijk, Inorg. Chim. Acta, 2006, 359, 4071–4078 CrossRef CAS; (f) S. Thakurta, P. Roy, G. Rosair, C. J. Gómez-García, E. Garribba and S. Mitra, Polyhedron, 2009, 28, 695–702 CrossRef CAS; (g) A. Ray, C. Rizzoli, G. Pilet, C. Desplanches, E. Garribba, E. Rentschler and S. Mitra, Eur. J. Inorg. Chem., 2009, 2915–2928 CrossRef CAS; (h) C. P. Pradeep and S. K. Das, Polyhedron, 2009, 28, 630–636 CrossRef CAS; (i) A. Ray, S. Mitra, A. D. Khalaji, C. Atmani, N. Cosquer, S. Triki, J. M. Clemente-Juan, S. Cardona-Serra, C. J. Gomez-Garcia, R. J. Butcher, E. Garribba and D. Xu, Inorg. Chim. Acta, 2010, 363, 3580–3588 CrossRef CAS; (j) S. Shit, M. Nandy, G. Rosair, M. S. El Fallah, J. Ribas, E. Garribba and S. Mitra, Polyhedron, 2013, 52, 963–969 CrossRef CAS.
- (a) A. Datta, J. K. Clegg, J.-H. Huang, A. Pevec, E. Garribba and M. Fondo, Inorg. Chem. Commun., 2012, 24, 216–220 CrossRef CAS; (b) K. Das, A. Datta, S. Roy, J. K. Clegg, E. Garribba, C. Sinha and H. Kara, Polyhedron, 2014, 78, 62–71 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1439835. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6ra10674a |
| This journal is © The Royal Society of Chemistry 2016 |