Competitive adsorption of a pool of pharmaceuticals onto a raw clay mineral

Abstract

The removal of a Pharmaceutically Active Compound (PhAC) pool using a well referenced clay mineral from Wyoming (SWy-2) as a geosorbent was studied for a better understanding of the environmental fate. As expected, the selected material shows its particular adsorption properties to PhAC under different experimental conditions with two main features depending on the chemical nature of the emerging micro-pollutants. Cationic PhACs, for which the driving force for their adsorption results from electrostatic interaction via the exchange with the inorganic cations of the clay mineral, are almost completely removed for all studied experimental conditions where it appears that the S/L ratio plays a minor role and the only one limitation for their removal is the cation exchange capacity of the adsorbent. In contrast, anionic and neutral PhACs are adsorbed to the clay mineral surface (silanol groups on the sheet edges, inorganic cations…) through other interactional mechanisms involving ion–dipole, van der Waals interaction, leading to a competition of all organic molecules where their chemical nature (electric charge, hydrophobicity) may also play a role in their adsorption. While the adsorption of ketoprofen, naproxen, diclofenac and salicylic acid anionic PhACs slightly increases with the increase of the S/L ratio, the removal of the neutral and the other anionic PhACs (gemfibrozil and ibuprofen) seems to be independent of that ratio and is particularly enhanced. The efficiency of the removal for a global pool of PhACs even in low S/L ratio stresses the control of the selected natural minerals on the dynamics of PhACs in the environment.

---

Introduction

Pharmaceutically Active Compounds (PhACs) are among the most concentrated (i.e. from several ng L⁻¹ to μg L⁻¹) and frequently detected organic micropollutants in natural waters,^1,2 which are now recognized to have significant toxic actions on numerous ecosystems. Indeed, in the presence of PhACs even at low concentration, both activity and boldness of several vertebrates can be altered.³ Moreover, since fish tissues show high concentration in both organic micropollutants and trace elements,⁴ it drives the contamination of the whole trophic chain. Conversely, some benthic invertebrate communities can be eradicated with exposure to contaminated sediments or/and PhACs.⁵ The low rate of PhACs removal in classical waste-water treatment plants^6,7 leads to a constant spillage in numerous aquatic compartments.^8,9

The understanding of both the dynamics of PhACs and their association with mineral phases in the environment is of primary importance to apprehend their pollution in water resources and toxic actions on various ecosystems. The properties and the chemical nature of PhACs and the characteristics of the suspended matter appear to control the partition between dissolved organic phase and mineral particle.¹⁰ The role of organic matter has been often highlighted but it is assumed that inorganic surfaces also play a key role on the transport on PhACs.^11,12 For example, PhACs are frequently sorbed onto sediments that can be used as a probe for a historical record of contamination of the environment.^13,14 Due to their large specific surface area and cation exchange capacity, clay minerals are among the most reactive mineral surfaces and were often used as adsorbents for both inorganic and organic pollutants.^15–17 The adsorption properties of these layered materials were highlighted in several applications from catalysis, nanocomposite materials, to geochemical barriers in the case of waste landfills.^18,19 Clay minerals and their organoclay derivatives were also proposed to be implemented in water treatment plants to improve the removal of organic pollutants.^20–22 In that way, several studies pointed out the excellent sorption properties of smectites for various PhACs such as: antibiotics,²³ and/or some psycho-active drugs.²⁴ For these cationic PhACs, or when they exhibit a positive electric charge in the studied pH range, the driving force for the adsorption leads to their intercalation within the interlayer space.^24–26 Anionic PhACs such as non-steroidal anti-inflammatory drugs, even for a concentration range at several mg L⁻¹, seemed to not be strongly adsorbed onto the studied clay minerals.^27,28 Nevertheless, in most research works related to clay minerals, the starting PhACs concentration for studying their adsorption was usually over-range, far more concentrated than that of the natural context. Moreover, the adsorption of PhACs onto natural clays was mainly undertaken for single,^22–26 or at maximum two molecules,²⁹ which allowed one to restrict the parameters to precisely emphasize the adsorption mechanisms rather than competition effects.

With the occurrence of numerous PhACs in water, it appears quite essential to stress out the sorption of several compounds in complex solutions onto a natural material. The starting concentration of PhACs in the range from 0.1 to 1 mg L⁻¹, slightly above their maximal environmental occurrence,¹ also appears as a key factor to evaluate the sorption in the environment. Thus, this study focuses on the ability of a raw smectite (SWy-2) to adsorb a complex PhACs (11 drugs) pool, which is at our knowledge the first time to be investigated, at concentrations close to those found in effluents or some surface waters, and for different parameters: (i) the solid/liquid ratio, (ii) the PhACs starting concentration and (iii) the competition effect. Finally, this study gives new insights on the dynamics of PhACs in the environment and evaluates the role of smectites on their environmental fate.

Materials and methods

Chemical reagents and clay mineral

The clay material was the SWy-2 montmorillonite (smectite from Crook County Wyoming, United States), supplied by the Source Clays Repository of the Clay Minerals Society. After <2 μm fractioning by sedimentation, the resulting SWy-2 was used without further purification to keep the starting material as raw as possible.

Eleven PhAC standards with a purity grade of >98%, showing different electric charges were selected in this study. Acetaminophen (ACE), atenolol (ATE), doxepin (DOX), gemfibrozil (GEM), ketoprofen (KET), metoprolol (MET), naproxen (NAP), salicylic acid (SCA), tramadol (TRA) were purchased from Sigma-Aldrich, whereas diclofenac (DCF) and ibuprofen (IBU) were obtained from Acros Organics (see Table 1 for details).

Table 1 Selected PhACs and their relevant characteristics in the present study: M_w the molecular weight, pK_a the acid/dissociation constant, log K_ow the octanol/water partition coefficient, S_w the solubility in water at 25 °C and charge the dominant form at pH = 7 values from ref. 30,^a and from ref. 31^b

PhAC	Abbreviation	Mw (g mol^−1)	pKa	log Kow	Sw^b (mg L^−1)	Charge state
Acetaminophen C8H9NO2	ACE	151.16	9.4^a	0.46^a	14 × 10^3	0
Carbamazepine C15H12N2O	CBZ	236.27	13.9^a	2.25^a	152	0
Diclofenac C14H11Cl2NO2	DCF	296.15	4.20^a	0.70^a	50 × 10^3	−
Doxepin C19H21NO	DOX	279.38	8.96^b	3.86^b	32 × 10^3	+
Gemfibrozil C15H22O3	GEM	250.33	4.8^b	4.33^b	4.97	−
Ibuprofen C13H18O2	IBU	206.28	4.9^a	3.50^a	21	−
Ketoprofen C16H14O3	KET	254.28	4.45^b	2.81^b	51	−
Metoprolol C15H25NO3	MET	267.36	9.6^b	1.79^b	4.777	+
Naproxen C14H14O3	NAP	230.26	4.2^a	3.18^a	15.9	−
Salicylic acid C7H6O3	SCA	138.12	3.5^a	1.19^a	11 × 10^3	−
Tramadol C16H25NO2	TRA	263.37	9.41^b	2.51^b	75 × 10^3	+

---

Sorption experiments

Batch equilibrium experiments were carried out in 1 L solution in triplicates for starting concentrations of each PhAC at 1, 0.5 and 0.1 mg L⁻¹ respectively and at a free pH and buffered by clay minerals between 6.8 and 7.2. Each 2 hours, some clay mineral was introduced in each bottle to reach total clay masses of 50 mg, 200 mg, 300 mg, 500 mg, 700 mg, 800 mg and 1 g respectively for a total time of 12 hours. The bottles were wrapped in aluminum foil during the experiment to prevent light-induced decomposition and were stirred for 2 hours at 500 rpm with a magnetic stirrer before and after each addition of clay. A volume of 10 mL of supernatant was taken before each clay addition, then filtered through a 0.2 μm membrane and frozen for further freeze-drying. Clays were recovered after the last supernatant sampling by centrifugation and drying at 60 °C.

The kinetic experiments were carried out following the same protocol as the equilibrium ones but by starting with a PhACs concentration of 1 mg L⁻¹ and a clay mineral mass of 500 mg in a single 1 L bottle.

Analytical methods

Liquid samples. Before being injected into a Gaseous Chromatography coupled with Mass Spectrometer (GC-MS), the samples were prepared following a derivatization step with MTBSTFA as De Oliveira et al. described.²²

Analyses were performed on a Trace Ultra GC coupled to a TSQ Quantum XLS MS equipped with an AS 3000 auto-sampler (both from Thermo Scientific). The GC was fitted with a Thermo Trace Gold TG-5 MS capillary column (60 m, length 0.25 mm internal diameter, 0.25 μm film thickness). The temperature of the column was held at 50 °C for 3 min, increased from 50 to 120 °C at 30 °C min⁻¹, and from 120 to 310 °C at 3 °C min⁻¹ with a final isothermal hold at 310 °C for 21 min. 2 μL of sample was injected in splitless mode at 280 °C. Helium was the carrier gas (1 mL min⁻¹). The MS was operated in electron ionization mode at 70 eV, from m/z 50 to 500. More details on the analytical performance are given in Table S1.†

Clay samples. X-ray diffraction (XRD) patterns were recorded between 2 and 64° (2θ) using a Thermo Electron ARL'XTRA diffractometer equipped with a Cu anode (Cu Kα_1,2 = 1.5418 Å) coupled with a Si(Li) solid detector. Experimental measurement parameters were 10 s counting time per 0.04° 2θ step.

The diffractograms were performed with dry powder samples (100 °C for 24 h). Carbon analyses were carried out using a Thermo Scientific Flash 2000 elemental analyzer assuming an analytical error of 0.05%.

Results

Kinetics experiment and modeling

The Fig. 1 shows the kinetics adsorption data of the tramadol (a cationic PhAC) and the ibuprofen as well as the gemfibrozil (anionic PhACs), which are representative to those of the studied organic compounds of each family.

Fig. 1 PhAC adsorbed amount onto SWy-2 as a function of time for IBU (white squares), GEM (white circles) and TRA (black circles).

As expected, the sorption behaviors mainly depend on the charge of the PhAC. Indeed, the equilibrium state for the sorption of the whole cationic PhACs was reached after 15 minutes leading to an adsorbed amount of 2 mg g⁻¹. The sorption kinetics of cationic PhACs is somehow faster than previous observations on cationic antibiotics where the equilibrium was reached after several hours for starting concentrations of 0.5 and 1 g L⁻¹ where the adsorbed positive charged organic molecules may exert electrostatic repulsion and thus reduce their sorption.^26,32

Although, the chemical nature of the selected cationic PhACs differs from antibiotics used previously, here the starting concentration for PhACs is lower leading to an increase of their mass transfer onto the clay mineral surface which is in agreement to past studies.^23,24 Thus, it is likely that the starting concentration may play a significant role relative to the kinetics and the mass transfer of PhACs to their equilibrium onto any adsorbent surface.

For both neutral and anionic species, where the removal was completed after 15 minutes, a steady state was obtained between 90 and 150 minutes (e.g. 1.4 mg g⁻¹ for GEM). Despite the low affinity of anionic PhACs to the clay mineral surface,²⁷ their removal was nonetheless remarkable, with minimum values around 70% for salicylic acid (SCA), leading to a significant equilibrium concentration at 0.28 mg L⁻¹ and mainly >90% for the other PhACs (Table 2).

Table 2 Experimental (Exp) and modeled equilibrium concentration (q_m), fitted parameters and correlation coefficients of sorption kinetic models, k₁, k₂, k_b and α_b are the pseudo first-order, pseudo second-order and Bangham sorption kinetics constants respectively, and r² is the correlation coefficient between the linearized observed and fitted data

Compound	Parameters
	Exp	First-order			Second-order			Bangham
	qm, mg g^−1	k1, min^−1	qm, mg g^−1	r^2, (—)	k2, mg g^−1 min^−1	qm, mg g^−1	r^2, (—)	kb, mg g^−1 min^−1	αb, (—)	r^2, (—)
Acetaminophen	1.95	2.30 × 10^−5	1.731	0.662	0.576	1.910	0.995	1.784	1.20 × 10^−2	0.911
Carbamazepine	1.99	1.38 × 10^−6	1.705	0.016	1.368	1.967	0.999	1.964	1.30 × 10^−3	0.103
Diclofenac	1.99	1.15 × 10^−5	1.708	0.805	1.252	1.982	0.999	1.928	4.70 × 10^−3	0.944
Doxepin	2.0	—	—	—	—	2.0	1.000	—	—	—
Gemfibrozil	1.71	6.91 × 10^−5	1.869	0.409	0.164	1.479	0.999	1.210	3.29 × 10^−2	0.672
Ibuprofen	1.87	1.15 × 10^−4	1.808	0.642	0.142	1.766	0.999	1.307	5.30 × 10^−2	0.913
Ketoprofen	1.92	1.15 × 10^−4	1.748	0.389	0.885	1.849	0.995	1.665	2.04 × 10^−2	0.751
Metoprolol	2.0	—	—	—	—	2.0	1.000	—	—	—
Naproxen	1.96	1.38 × 10^−5	1.721	0.401	1.473	1.907	0.999	1.887	2.70 × 10^−3	0.417
Salicylic acid	1.77	6.91 × 10^−5	1.849	0.629	0.206	1.447	0.999	1.281	3.13 × 10^−2	0.744
Tramadol	2.0	—	—	—	—	2.0	1.000	—	—	—

---

To identify the mechanisms of adsorption, the potential removal rate and the control of the steps involved in the processes, the pseudo first-order, second-order and the Bangham kinetic models were used as follows in their linear form respectively:^24,28

log q_t = log k_b + α_b log t

with q_t the sorbed concentration in mg g⁻¹ at the time t (min), q_m the pseudo-equilibrium sorbed concentration (mg g⁻¹), k₁ (min⁻¹), k₂ (mg g⁻¹ min⁻¹), k_b (mg g⁻¹ min⁻¹) and α_b respectively the first-order, the second-order and the Bangham sorption rate constants.

Based on the obtained correlation coefficients r² of the three tested models (Table 2), it appears that the experimental data are better adjusted with the pseudo second-order kinetic model (r² comprised between 0.995 and 0.999). Although the pseudo second-order kinetic model is based on the assumption that the adsorption is chemically achieved,³³ several studies reported good fits with this model despite the driving force for the adsorption follows other mechanisms.^34–36 It seems that the pseudo-first and the Bangham equations do not fit well with experimental data.

The modeling of cationic PhACs adsorption kinetic is impossible due to their total adsorption since the first sample (i.e. q_t < LOD).

Concerning both neutral and anionic PhACs, the starting concentration affects the kinetics for adsorption with large value for pseudo-second order rate constant k₂ which is consistent with the short time for the equilibrium adsorption. Here, the rate of chemical interactions between PhACs and the accessible sites of the clay mineral represents the step that controls the overall kinetics of the processes.

Adsorption equilibrium experiments

Modeling. The fit of the resulting adsorption isotherms by using Freundlich equation models drives to numerous thermodynamic parameters allowing one to precisely quantify the affinity of both PhACs with the geosorbent. Briefly, the linear Freundlich equation is written as:^28,37
with q_e the PhAC adsorbed amount at equilibrium (mol g⁻¹), C_e the PhAC equilibrium concentration in the supernatant (mol L⁻¹), K_F the Freundlich affinity constant (L g⁻¹), that quantifies the extent of adsorption and n a constant indicating the degree of non-linearity between PhAC and the adsorbent.

Concerning cationic PhACs (DOX, TRA and MET) the selected equation model was unlikely to apply due to the total adsorption (i.e. q_e < LOD) whatever the starting concentration or the solid/liquid ratio.

In contrast, both nonionic and anionic PhACs adsorption isotherms are well fitted by Freundlich model.

Nevertheless, it appears that the agreement between the Freundlich fits and experimental data generally decreases with the starting PhAC concentration (Table 3) due to the proportional increase in the experimental errors. Fits remained in good agreement with the data with correlation coefficients mostly higher than 0.95, allowing us to put forward some interpretations of the results.

Table 3 Freundlich fit parameters and solid–water partition characterization with the mean log K_d values (K_d in L kg⁻¹) and Relative Standard Deviation (RSD) values and his statistical significance <1% of the mean for ** and <5% of the mean for *

		Starting concentration		Freundlich			Solid–water partition
		PhAC	μg L^−1	ln KF (L g^−1)	n	r^2	log Kd	RSD
Group 1	Neutral	ACE	1000	−7.56	1.49	0.971	4.26	0.029**
			500	1.81	0.71	0.986	4.63	0.027**
			100	7.89	0.51	0.882	5.22	0.121*
		CBZ	1000	−5.67	1.44	0.915	3.94	0.037**
			500	−3.61	0.99	0.987	4.69	0.036**
			100	0.62	0.74	0.928	4.68	0.050*
	Anionic	GEM	1000	−4.00	1.20	0.989	3.54	0.009**
			500	−1.45	1.02	0.944	3.86	0.009**
			100	1.26	0.77	0.916	4.29	0.059*
		IBU	1000	−0.42	0.89	0.975	3.73	0.014**
			500	5.71	0.62	0.965	3.83	0.028**
			100	19.41	0.39	0.870	4.12	0.104*
Group 2		DIC	1000	48.66	0.20	0.919	3.75	0.101*
			500	21.15	0.36	0.969	4.08	0.161*
			100	1.75	0.65	0.913	4.46	0.086*
		KET	1000	24.49	0.31	0.959	3.95	0.079*
			500	5.31	0.62	0.917	3.99	0.061*
			100	−3.35	0.98	0.989	4.66	0.060*
		NAP	1000	7.10	0.55	0.970	4.11	0.049*
			500	4.97	0.59	0.954	4.51	0.059*
			100	−8.27	1.55	0.979	4.57	0.045*
		SCA	1000	41.69	0.21	0.951	3.57	0.071*
			500	−2.62	1.04	0.928	3.89	0.041*
			100	−6.11	1.22	0.933	4.62	0.027**

---

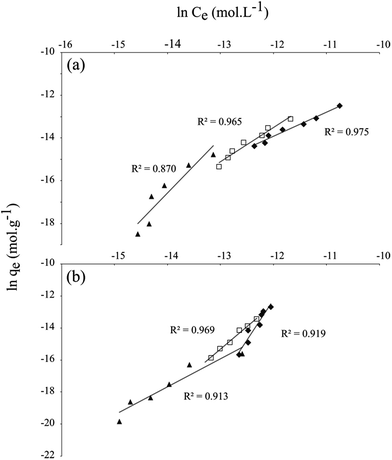
Two trends emerged based on the analysis of the Freundlich parameters derived from the fitting procedure (Table 2). Four PhACs: ACE, CBZ, GEM and IBU (labeled as group 1) show both a high K_F and a low n values for a low starting concentration regime, whereas for DIC, KET, NAP and SCA (group 2), an opposite behavior is observed (Fig. 2a and b). Interestingly, the attribution of PhACs group does not follow the charge of the organic molecules where for example group 1 includes a mix of neutral (ACE and CBZ) and anionic (GEM and IBU) PhACs but may be related to their hydrophobic behavior.

Fig. 2 Adsorption isotherms of (a) IBU and (b) DIC onto SWy-2 for starting concentrations of 0.1 mg L⁻¹ (triangles), 0.5 mg L⁻¹ (squares) and 1 mg L⁻¹ (diamonds). Solid lines represent the Freundlich model fits and r² their coefficients of determination.

Solid/water partition. Further information can be obtained with the use of the solid/water partition coefficient K_d (L kg⁻¹) of each PhAC with respect to the clay mineral, which can be determined with the following equation:³⁸
where q_e corresponds to the PhAC sorbed concentration (mol kg⁻¹) and C_e the PhAC equilibrium concentration (mol L⁻¹).

log K_d values for the different neutral or anionic species exhibit the same trend shown in the Table 3.

The lower the starting concentration, the higher the log K_d, which underlines that the partition is enhanced by the reduction of the starting concentration, indicating a higher affinity to the clay mineral surface. However, the partition coefficients did not fluctuate once the solid/liquid ratio evolved (Fig. 3) with RSD values <5% of the mean for the whole tests (Table 2). This indicates that the affinity of PhACs to the clay mineral does not strongly depend on the solid/liquid ratio but mainly on the solid/water partition values.

Fig. 3 Evolution of the solid–water partition of PhACs (log K_d) by the addition of SWy-2 affecting the solid/liquid ratio for (a) ACE (black markers) and (b) KET (white markers) for starting concentrations of 0.5 mg L⁻¹ (squares) and 1 mg L⁻¹ (diamonds), error bars correspond to experimental triplicates.

The logarithm of the partition coefficient K_d shows two distinct behavior following the chemical nature of PhACs and reinforces the idea of two groups for the organic molecules that exhibit different affinity to the clay mineral surface (Fig. 3a and b). Indeed, for the two highest concentrations (i.e. 0.5 and 1 mg L⁻¹). The group 1 including ACE, CBZ, GEM and IBU PhACs exhibits an absence of variation of log K_d for the whole studied solid/liquid ratio with RSD < 1% to the mean value. This indicates that the introduction of accessible adsorption sites in the solution that provides the addition of clay mineral rigorously leads to the same sorption properties (Fig. 3a). In the opposite, the group 2 with DIC, KET, NAP and SCA PhACs, the RSD values vary between 1 and 5% of the mean value (Table 3) which underlines a slight dependence of the coefficient partition (i.e. log K_d) with the added masses of clay minerals.

This feature may underline a certain competition effect between PhACs at low accessible surface (i.e. low clay mineral mass regime), which has less importance once are introduced large amounts of clay mineral in solution since it drives to a large accessible sites for adsorption.

Clays characterization

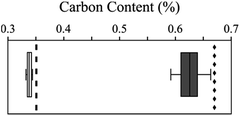
The proper adsorption of the whole PhACs was confirmed by elemental analyses (Fig. 4). Indeed, if one considers a PhACs removal of 100%, the comparison of the expected maximum carbon percentage to the elemental results indicate that the decrease of the PhAC concentration in the solution does not result to any degradation (although this hypothesis was obviously not valid since PhACs leads to environmental problem on decades) but to sorption onto clay mineral surface.

Fig. 4 Carbon percentage of clays after experiments at 0.5 mg L⁻¹ (white box; n = 6) and 1 mg L⁻¹ (grey box; n = 6), the line within the box marks the median, boundaries indicates 25th and the 75th percentile respectively and error bars indicate the minimum and maximum values; the calculated carbon percentage for a total removal is represented for 0.5 mg L⁻¹ (black dotted line) and 1 mg L⁻¹ (black diamond line), the 6 analyzed samples correspond to an analytical replicate for each experimental triplicate.

Elemental analyses leads to a removal rate equals to 97.5% and 94.2% (n = 6) at the starting concentrations of 0.5 and 1 mg L⁻¹ respectively. These results stress out that the adsorption onto clay minerals is more efficient at a low starting concentration regime.

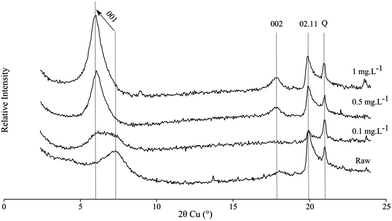
X-ray diffraction represents an important tool for the understating of the structural changes in clay minerals by following the 00l reflection exhibiting probable intercalation of organic compounds in one hand and at large angular values; it can provide information on a possible crystallization of PhAC on the external surface of the phyllosilicates. The X-ray diffraction patterns of the dehydrated raw smectite show a wide 001 reflection at about 7.5° (2θ) corresponding to a d₀₀₁ spacing of 9.7 Å. After being in contact to a solution with a pool of PhACs, the 00l reflection shifts to low angular value with d₀₀₁ interlayer spacing at 11 and 12.7 Å for the two highest starting concentrations (Fig. 5). In the aim of comparison, the diffractograms of three PhACs in single solution are given in Fig. S2,† observing the same trends than in multi-component solutions.

Fig. 5 X-ray diffractograms of clay mineral samples before (Raw) and after interactions with the 11 PhACs pool solutions at starting concentrations of 0.1, 0.5 and 1 mg L⁻¹. Q corresponds to the quartz, impurity, which is commonly associated with the SWy-2 clay mineral.

Discussion

The swelling of the clay mineral highlighted with the increase of the interlayer space shows a possible intercalation of PhAC molecules. Nevertheless, it is rather hard to identify the nature of the PhAC molecule located within the interlayer space. However, the spontaneous and total adsorption of cationic PhACs whatever the experimental conditions, combined with the small increase of the global d₀₀₁ spacing (i.e. 3 Å), indicate that cationic PhAC molecules may be organized in a lateral monolayer arrangement into the interlayer space.

Moreover, the increase of the interlayer spacing is consistent with the molecular thickness of MET, DOX and TRA, the three selected cationic compounds.^39–41

Thus, this observation demonstrates that the whole surface (i.e. internal and external) of clay mineral is accessible for the adsorption leading to multiple possibilities for the interactional mechanisms with PhACs.

As a result, cationic PhACs are primarily adsorbed conferring a hydrophobic behavior to some parts of the clay mineral surface and/or leading to a competition for the further adsorption of PhACs.⁴² The generation of a hydrophobic network with the adsorption of organic cations such as surfactants for instance was successfully used for the adsorption of various kind of organic pollutants. However, here the concentration of the whole cationic PhACs is below the CEC and represents up to 26% of the CEC of the clay minerals for the maximum starting concentration of PhACs (1 mg L⁻¹) and the minimum solid/liquid ratio (50 mg L⁻¹). Thus, such hydrophobic effect may play a minor part but does not mean it may be completely excluded in the sorption mechanisms as a comparison to the other adsorption sites clay mineral surface provides.

In this study, the pH was set free at a value of 6.8 near the point of zero charge of the edge sites of the clay minerals,⁴³ and thus may slightly contribute to the PhACs adsorption.

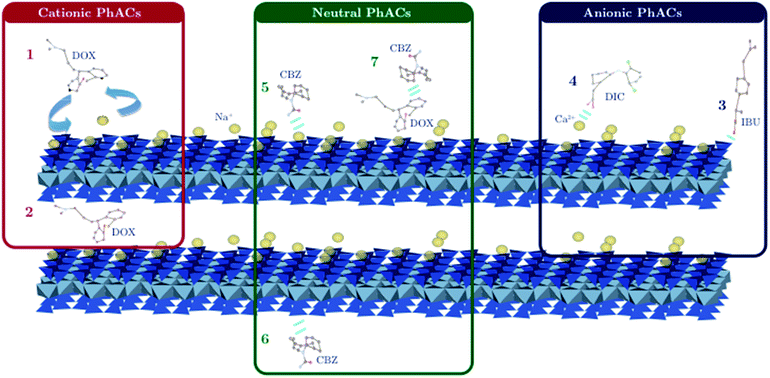
Nevertheless, pH fluctuations can occur (up to 7.2 in the case of the maximum clay mass) leading to a significant role of the edge adsorption sites, (i.e. silanol or aluminol groups) that can interact through hydrogen bonds with both anionic and neutral PhACs. However, the presence of Ca²⁺ divalent cations may also be responsible for the adsorption of both anionic and neutral PhACs through ion–dipole interaction (i.e. cationic bridge) (Fig. 6).³⁸

Fig. 6 Sorption mechanisms of PhACs onto clay mineral function of their charge, with (1) and (2) a cation exchange with the example of doxepin (DOX), (3) sorption onto edge sites and (4) cationic bridge with the example of diclofenac (DIC), (5) n–π electron donor/acceptor interaction, (6) hydrogen bond with the example of carbamazepine (CBZ) and (7) hydrophobic interaction.

Indeed, Ca²⁺ has been identified to favor the adsorption of organic matter such as humic acids for the generation of clay–humic complex,⁴⁴ although it is rather hard to distinguish and to quantify which adsorption mechanism is the most preponderant.

The adsorption isotherms allowed us to class PhACs in two groups if one excludes cationic PhACs where both adsorption mechanism and kinetics completely differ from anionic and neutral PhACs. These two groups show different evolution of the coefficient of partition log K_d, which was identified as a key parameter for the understanding of the adsorption of PhACs, with the addition of clay mineral in solution.^45,46 ACE, CBZ, GEM and IBU (group 1) do not show any variation of the partition, while log K_d significantly increases with the addition of clay mineral underscoring a possible competition effect for the 4 anionic PhACs in the group 2. Interestingly, the behavior of K_d with the solid/liquid ratio does not depend on the electric charge of PhACs but on their hydrophobic behavior. Indeed, IBU and GEM with a single aromatic ring in their chemical skeleton own a high log K_ow value (Table 1) seem to be preferentially adsorbed compared to the other anionic PhACs DIC, NAP and KET that show two aromatic rings. Yu and Bi focused on the adsorption of naproxen,⁴⁵ an anionic PhAC, and stressed out the importance of n–π electron/donor acceptor (EDA) interactional mechanism with clay mineral. Although it is rather hard to point out the main adsorption driving force in a pool of PhACs, EDA mechanism may also play in the adsorption of IBU and GEM and could be one reason among those of the hydrophobic media generating through the primer adsorption of cationic PhACs favoring the adsorption of hydrophobic PhAC (or those showing a high log K_ow) and/or the possible association with cationic PhAC to the difference with their analogous PhACs.

If the adsorption of cationic PhACs is well understood and involves strong electrostatic interaction, the scenario is far more complex for both neutral and anionic PhACs where several interaction mechanisms are involved as well as the competition of a pool of PhAC molecules to the adsorption sites. Once the solid to liquid ratio changes, the removal of both neutral and anionic PhACs are strongly impacted while log K_d values do not fluctuate so far. Indeed, their removal vary between 80 and 100% at the highest mass of clay mineral (Table 4).

Table 4 Removal efficiency for the lowest and the highest added clay mineral mass (50 and 1000 mg) at a PhACs starting concentration of: 0.1, 0.5 and 1 mg L⁻¹ respectively

PhAC	Clay mass (mg)	Mean removal efficiency (%) at
		0.1 mg L^−1	0.5 mg L^−1	1 mg L^−1
Acetaminophen	50	73.9	76.0	35.1
	1000	99.9	96.5	95.3
Carbamazepine	50	68.3	66.5	32.6
	1000	99.9	98.7	84.8
Diclofenac	50	50.4	13.3	8.6
	1000	99.3	99.9	95.4
Gemfibrozil	50	46.3	31.7	14.0
	1000	99.9	87.1	73.3
Ibuprofen	50	20.3	17.6	22.1
	1000	98.1	91.0	88.3
Ketoprofen	50	61.3	16.4	11.9
	1000	99.4	97.7	96.0
Naproxen	50	74.0	44.4	24.0
	1000	98.6	98.4	94.5
Salicylic acid	50	72.9	16.1	7.1
	1000	97.9	90.6	88.9

---

Thus, it appears that the best experimental conditions for the non-cationic PhACs removal are at a low PhAC starting concentration with a large amount of clay mineral (i.e. at high solid/liquid ratio) with numerous accessible sites for adsorption. It can also be noted that the solid/water partition, enhanced by reducing the starting concentration, is generally linear. It means that in environmental conditions, clay minerals could sorbed a constant amount of non-cationic PhACs, depending on the starting concentration, the hydrophobicity of each compound and the solid/liquid ratio.

The chosen starting material, used without any purification, can be considered as a natural equivalent of natural smectites. Nevertheless, natural smectites are often less pure than SWy-2, often used as standard materials. The impact of impurities is difficult to evaluate, but we can assume that the compensating cations played a key role. The occurrence of divalent cations, sparsely present in SWy-2 but more present in other bentonites could favor the sorption capacity of these latter.

Conclusions

Beyond the excellent sorption capacity of natural montmorillonite, this work provides new insights about the parameters that control the competition for adsorption for a pool of pharmaceuticals onto a raw clay mineral.

The complete removal of cationic PhACs results to a cation exchange with the accessible inorganic cations of the clay mineral whereas for both anionic and neutral species, the removal is strongly enhanced with the increase of the solid–liquid ratio. Anionic PhACs are favorably adsorbed at a low starting concentration and for the highest solid–liquid ratio. However, not all anionic PhACs are sorbed to the same extent due to competition effect. Gemfibrozil and ibuprofen due to their more pronounced hydrophobic nature show a significantly better sorption than those of ketoprofen, naproxen, diclofenac and salicylic acid.

Thus, beyond the molecular charge that controls the sorption mechanisms, other factors as hydrophobicity and structure of the PhAC play an important role in the magnitude of adsorption of non-cationic compounds.

The environmental fate of pharmaceuticals results to their possible association with suspended inorganic surfaces, such as raw smectite clays. These minerals represent, as shown in this study, a potential way of transport through the environment. This adsorption study, performed without organic matter, finally demonstrates that clays represented a potential adsorbent, even for non-ionic or anionic species, if used in appropriate conditions. Nevertheless, the use of these materials for the water purification necessitate further tests on recycling possibilities.

Acknowledgements

The work received financial support from the HArPE Project (2012-00073536) funded by the Région Centre. The authors would also like to thank Marielle Hatton for carbon elemental analysis.

References

1. R. Loos, B. M. Gawlik, G. Locoro, E. Rimaviciute, S. Contini and G. Bidoglio, Environ. Pollut., 2009, 157, 561–568.
2. E. Vulliet and C. Cren-Olivé, Environ. Pollut., 2011, 159, 2929–2934.
3. T. Brodin, J. Fick, M. Jonsson and J. Klaminder, Science, 2013, 339, 814–815.
4. K. Grabicova, R. H. Lindberg, M. Östman, R. Grabic, T. Randak, D. G. Joakim Larsson and J. Fick, Sci. Total Environ., 2014, 488–489, 46–50.
5. N. de Castro-Català, M. Kuzmanovic, N. Roig, J. Sierra, A. Ginebreda, D. Barceló, S. Pérez, M. Petrovic, Y. Picó, M. Schuhmacher and I. Muñoz, Sci. Total Environ., 2016, 540, 324–333.
6. B. Petrie, E. J. McAdam, M. D. Scrimshaw, J. N. Lester and E. Cartmell, TrAC, Trends Anal. Chem., 2013, 49, 145–159.
7. P. Verlicchi, M. Al Aukidy and E. Zambello, Sci. Total Environ., 2012, 429, 123–155.
8. S. Mompelat, B. Le Bot and O. Thomas, Environ. Int., 2009, 35, 803–814.
9. T. Deblonde, C. Cossu-Leguille and P. Hartemann, Int. J. Hyg. Environ. Health, 2011, 214, 442–448.
10. B. F. da Silva, A. Jelic, R. López-Serna, A. A. Mozeto, M. Petrovic and D. Barceló, Chemosphere, 2011, 85, 1331–1339.
11. A. Maoz and B. Chefetz, Water Res., 2010, 44, 981–989.
12. J. C. Durán-Álvarez, B. Prado-Pano and B. Jiménez-Cisneros, Chemosphere, 2012, 88, 84–90.
13. J. Klaminder, T. Brodin, A. Sundelin, N. J. Anderson, J. Fahlman, M. Jonsson and J. Fick, Environ. Sci. Technol., 2015, 49, 10406–10412.
14. F. Tamtam, B. Le Bot, T. Dinh, S. Mompelat, J. Eurin, M. Chevreuil, P. Bonté, J.-M. Mouchel and S. Ayrault, J. Soils Sediments, 2011, 11, 852–859.
15. G. Lagaly, R. M. Barrer and K. Goulding, Philos. Trans.: Math., Phys. Eng. Sci., 1984, 311, 315–332.
16. O. Abollino, M. Aceto, M. Malandrino, C. Sarzanini and E. Mentasti, Water Res., 2003, 37, 1619–1627.
17. A. Mahamat Ahmat, M. Boussafir, C. Le Milbeau, R. Guegan, J. Valdès, M. Guiñez, A. Sifeddine and L. Le Forestier, Mar. Chem., 2016, 179, 23–33.
18. F. T. Madsen, Clay Miner., 1998, 33, 109–129.
19. L. A. de S Rodrigues, A. Figueiras, F. Veiga, R. M. de Freitas, L. C. C. Nunes, E. C. da Silva Filho and C. M. da Silva Leite, Colloids Surf., B, 2013, 103, 642–651.
20. V. K. Gupta, I. Ali, T. A. Saleh, A. Nayak and S. Agarwal, RSC Adv., 2012, 2, 6380–6388.
21. T. Thiebault, M. Boussafir, R. Guégan, C. L. Milbeau and L. L. Forestier, Environ. Sci.: Water Res. Technol., 2016, 2, 529–538.
22. T. De Oliveira, R. Guégan, T. Thiebault, C. L. Milbeau, F. Muller, V. Teixeira, M. Giovanela and M. Boussafir, J. Hazard. Mater., 2016.
23. W. Yan, S. Hu and C. Jing, J. Colloid Interface Sci., 2012, 372, 141–147.
24. P.-H. Chang, W.-T. Jiang, Z. Li, C.-Y. Kuo, J.-S. Jean, W.-R. Chen and G. Lv, J. Hazard. Mater., 2014, 277, 44–52.
25. T. Thiebault, R. Guégan and M. Boussafir, J. Colloid Interface Sci., 2015, 453, 1–8.
26. Z. Li, P.-H. Chang, J.-S. Jean, W.-T. Jiang and C.-J. Wang, J. Colloid Interface Sci., 2010, 341, 311–319.
27. S. K. Behera, S. Y. Oh and H. S. Park, Int. J. Environ. Sci. Technol., 2012, 9, 85–94.
28. E. Çalışkan Salihi and M. Mahramanlıoğlu, Appl. Clay Sci., 2014, 101, 381–389.
29. H. Mansouri, R. J. Carmona, A. Gomis-Berenguer, S. Souissi-Najar, A. Ouederni and C. O. Ania, J. Colloid Interface Sci., 2015, 449, 252–260.
30. O. A. H. Jones, N. Voulvoulis and J. N. Lester, Water Res., 2002, 36, 5013–5022.
31. DrugBank Database, drugbank.ca.
32. P.-H. Chang, Z. Li, J.-S. Jean, W.-T. Jiang, C.-J. Wang and K.-H. Lin, Clay Water Treat., 2012, 67–68, 158–163.
33. Y. Ho and G. McKay, Process Biochem., 1999, 34, 451–465.
34. V. Martínez-Hernández, R. Meffe, S. Herrera, E. Arranz and I. de Bustamante, Sci. Total Environ., 2014, 472, 273–281.
35. V. Martínez-Hernández, R. Meffe, S. Herrera López and I. de Bustamante, Sci. Total Environ., 2016, 559, 232–241.
36. Q. Zhang, L. Zhao, Y. Dong and G. Huang, J. Environ. Manage., 2012, 102, 165–172.
37. R. Guégan, M. Giovanela, F. Warmont and M. Motelica-Heino, J. Colloid Interface Sci., 2015, 437, 71–79.
38. T. Thiebault, M. Boussafir, R. Guegan, C. le Milbeau and L. Le Forestier, Environ. Sci.: Water Res. Technol., 2016, 2, 529–538.
39. Y. Chen, A. Zhou, B. Liu and J. Liang, Appl. Clay Sci., 2010, 49, 108–112.
40. E. Ghedini, M. Signoretto, F. Pinna, V. Crocellà, L. Bertinetti and G. Cerrato, Microporous Mesoporous Mater., 2010, 132, 258–267.
41. N. Rajendiran, R. K. Sankaranarayanan and J. Saravanan, J. Mol. Struct., 2014, 1067, 252–260.
42. R. Guégan, Langmuir, 2010, 26, 19175–19180.
43. E. Tombácz, Z. Libor, E. Illés, A. Majzik and E. Klumpp, Org. Geochem., 2004, 35, 257–267.
44. A. Majzik and E. Tombácz, Org. Geochem., 2007, 38, 1319–1329.
45. C. Yu and E. Bi, Chemosphere, 2015, 138, 335–339.
46. W. Zhang, Y. Ding, S. A. Boyd, B. J. Teppen and H. Li, Chemosphere, 2010, 81, 954–960.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra10655b

---