Utilization of a pyrrole derivative based antimicrobial functionality impregnated onto CaO/g-C3N4 for dyes adsorption
Abstract
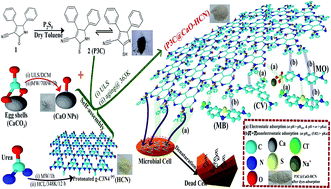
A novel functionalization of CaO/g-C3N4 based nanocomposite using 4,5-diphenyl-2-thioxo-2,5-dihydro-1H-pyrrole-3-cabonitrile (P3C@CaO–HCN) was performed for wastewater remediation from organic dyes and microbial pollutants. Adsorption performance of multiple mixtures of basic and acidic dyes by P3C@CaO–HCN was investigated and optimized using a three-level Box–Behnken design of experiment (BBD-DOE). The quadratic Box–Behnken polynomial equation showed the best fit with experimental adsorption capacities of crystal violet (CV), methylene blue (MB), and methyl orange (MO) model dyes. The simultaneous influence of adsorption conditions was tested based on the developed Box–Behnken equation, 3D contour plots, and ANOVA analysis. Nonlinear regression analysis of kinetics and isotherm constants were computed and validated to propose the adsorption mechanism. Adsorption was found within the ranges of endothermic physical adsorption (ΔH° = 6.17 to 8.58 kJ mol−1) and controlled by both π–π and electrostatic forces depending on the pH level in addition to film diffusion mechanism. The maximum adsorption affinity can be arranged in the order of MB > CV ≥ MO with qe (µmol g−1) of 1915.8, 1227.8, and 1221 µmol g−1, respectively. At 500 mg L−1 P3C@CaO–HCN as the minimum inhibitory dose, the inhibition rates (I%) were 87.9%, 46.9%, and 72.5% for E. coli, P. aeruginosa, and C. albicans, respectively. The antimicrobial effect can result from the free cyanide (C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N) functionality of a pyrrole-3-cabonitrile and protonated g-C3N4 (HCN) sheet, which depends on the P3C@CaO–HCN concentration and pathogen types.
N) functionality of a pyrrole-3-cabonitrile and protonated g-C3N4 (HCN) sheet, which depends on the P3C@CaO–HCN concentration and pathogen types.

 Please wait while we load your content...
Please wait while we load your content...