Molecular relaxation and dynamic rheology of “cluster phase”-free ionomers based on lanthanum(III)-neutralized low-carboxylated poly(methyl methacrylate)

Abstract

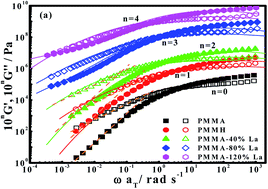
Molecular dynamics and linear dynamic rheology of La(III)-neutralized low-carboxylated poly(methyl methacrylate) (PMMA) ionomers with varying neutralization levels are investigated. While the ionomers do not form a clear cluster phase, increasing neutralization level causes notable retardation of the α relaxation and elevation of glass transition temperature. In addition, dynamic rheology of the ionomer melt follows the time–temperature superposition principle and, at neutralization levels above 80%, shows a long-term relaxation process and nonterminal relaxation ascribed to ionic species. Especially the ionomer with a neutralization level of 120% behaves like a critical gel. The long-term relaxation process is well described in terms of Cole–Cole curves, relaxation time spectra, complex viscosity and loss tangent. By analyzing the linear rheology in the framework of a “two phase” model, an interconnected multiplets network is identified as a mechanism being responsible for the fluid-to-solid transition of “cluster phase”-free ionomers with increasing neutralization level.

---

Introduction

There has been a long-standing interest in ionomers that show a variety of applications in chemically resistant thermoplastics, selectively permeable ion-transport membranes, self-healing and shape memory materials and so on.¹ Ionomers are constituted by hydrophobic polymeric backbones bearing small amounts (usually less than 15 mol%) of covalently attached side/end ionic groups, typically acid groups neutralized with metal cations.² The ionic species, via electrostatic interaction or ionic supramolecular bonding,³ usually associate into ionic aggregates⁴ behaving as physical crosslinks in the matrix of low dielectric constant and low ionic solvating ability.^5,6 The structure of ionomers has been characterized via small angle X-ray scattering (SAXS), transmission electron microscopy, and nuclear magnetic resonance and so on,^7–13 and several models^14–20 have been proposed to account for the structure. According to the multiplet-cluster model,^14,15 at low ion contents, the ion pairs form multiplets (less than 3 nm) surrounded by polymer segments with restricted mobility. With increasing ion content, the regions of restricted mobility gradually overlap to form an ion-rich “cluster phase” with an individual T_g penetrating throughout the ion-poor matrix phase,^21–23 which has been verified in various ionomers.^{2,15,20,24,25} In general, the morphologies^21,22,26,27 of ionomers are dependent on the nature of the matrix^15,28–30 as well as the ion content, neutralization level, and type of cations used to neutralize the anionic groups.^25,31–34

The relaxation behavior of ionomers is greatly affected by the structure of ionic aggregates and its resulting morphologies, thus significantly altering the physical and mechanical properties of the ionomers compared to their nonionic counterparts.^35–39 As an example, the ionic associations acting as multifunctional “electrostatic” crosslinks⁴⁰ greatly slow down the segmental relaxation and increase the glass transition temperature²⁰ of the matrix and induce a microphase-separated ionic cluster.⁴¹ In the other hand, the melt rheology of ionomers is generally related to both terminal relaxation of polymer chains and the “ion-hopping” relaxation of ionic associations and the latter is assumed to have a finite lifetime reflecting the average length of time an ionic group spending in a particular aggregate.

A sol-to-gel transition is predicted for ionomers carrying one ionic groups per chain serving as crosslinking sites.⁴² The ionomers below but very close to the gel point show a relaxation similar to chemical gels whereas those near and beyond the gel point show a well-defined plateau before terminal relaxation controlled by ionic dissociation.⁴³ The effect is so marked that even oligomeric ionomers may exhibit linear viscoelasticity similar to melts of well-entangled counterparts⁴⁴ assigned to the formation of a temporary supramolecular network of spatially distributed clusters.^45,46 When there is no glass transition of the multiplet phase, the rheology and diffusion of ionomers could be interpreted in terms of a reptation model, modified to account for the additional constraints on individual chain motion imposed by the associating ion pairs.⁴⁷ The chain diffusion via hindered reptation is slowed down by repetitive association/dissociation.^48–50 The hindered fluctuations affect dynamics of moderately entangled chain while hindered reptation dominates the relaxation of well entangled chains.⁵¹ The ionomers with low ion contents exhibit glassy and delayed rubbery relaxation following sticky Rouse model taking the lifetime of ionic association into consideration.^5,52 At temperatures between two T_gs, the Guth and Halpin–Tsai relations can be applied to linear modulus as a function of volume fraction of clusters, the rigid species being regarded as filler particles dispersed in a soft continuous matrix.^40,53,54 When ionic aggregates percolate^21–23 and the counterion diffusion is involved in collective rearrangements rather than hopping⁵⁵ at high ion contents, the glassy and rubbery relaxation moduli merge into one broad process following Kohlrausch–Williams–Watts equation over an extremely wide range of time scale.⁵² Here, the ionomers might be regarded as a soft filler-continuous cluster system whose mechanical properties could be interpreted in terms of percolation concepts or logarithmic mixing.^40,53,54 However, it is still a giant challenge to distinguish the gelation by ionic complexes^42,43,47 or the percolation by the cluster phase.^53,54 It is still lack of investigations about the influence of neutralization degree on the dynamics and rheology of low charged ionomers.

Poly(methyl methacrylate) (PMMA)-based ionomers have been used as models for studying characteristics of ionic associations.^15,76–81 Since the relaxation of ionomers can be altered simply by varying neutralization degrees and cation types,^56–60 we herein synthesize ionomers based on La(III)-neutralized low-carboxylated (2.50 mol%) PMMA (PMMH) to investigate the influence of neutralization level on the segmental dynamics and dynamic rheology. It is found that the ionomers do not form a cluster phase up to a neutralization level as high as 120% where the materials behave gel-like. A new gelation mechanism is proposed for accounting for the rheological fluid-to-solid transition with respect to neutralization level.

Experimental

Materials and sample preparation

Poly(methyl methacrylate) (PMMA) (weight averaged molecular weight M_w ≈ 9.0 × 10⁴, polydispersity M_n/M_w = 1.47) from LG Co. Ltd., South Korea was used as received. Carboxylated PMMA (PMMH) was prepared by saponification of PMMA using sodium hydroxide (NaOH) in tetrahydrofuran/deionized water (1/1 by mass ratio) mixture solvent, and acidification with excess hydrochloric acid. PMMH was collected by dropping the suspension into deionized water and washing for several times, followed by filtration and drying under vacuum at 80 °C for 48 h. The acid content of PMMH was determined as 2.50 mol% by titration, which corresponds to 22.3 acids per macromolecule or the acid groups are spaced by approximately 76 carbons along the polymer backbones. No Na(I) could be detected by using Inductively Coupled Plasma-Atomic Emission Spectrometry.

The ionomers were obtained by adding a methanol solution of sodium acetate/lanthanum chloride (3/1 by molar ratio) dropwise to a tetrahydrofuran/methanol (5/1 by volume ratio) solution of PMMH under stirring to achieve varying degrees of neutralization. The resultant solution after stirred for 3 h under reflux was precipitated and washed with methanol. The ionomers recovered by filtration and dried under vacuum at 80 °C for 72 h were named as PMMA-xLa, where x is the degree of neutralization (x = 40%, 80%, 120%) estimated by La(III) content determined by Inductively Coupled Plasma-Atomic Emission Spectrometry. The remnant Na(I) detected was neglectable small, being 0.33% of La(III) content in the ionomer PMMA-120% La. According to DC conductivity (σ) obtained from dielectric spectra (Fig. S1†), σ gradually decreases with the increasing content of La(III) due to its coordination with carboxylic acid. It is thus proofed that there is little amount of free lanthanum ions. The overneutralized ionomer may contain lanthanum acetate bonded on the macromolecular chain or trapped in the ionic aggregates.⁶¹ The ionomers were hot pressed at 180 °C under 14 MPa for 8 min to form films that were further annealed at 120 °C for 5 days.

Fourier transform infrared study

About 1.0 mg sample was ground together with 200 mg dried potassium bromide powder in an agate bowl. The mixture was pressed into transparent slice under pressure. Fourier transform infrared spectroscopy (FTIR) measurements were carried out on a spectrometer (Nicolet 6700, Thermo Fisher Scientific LLC, USA) with 2 cm⁻¹ resolution and 64 scans at room temperature.

Small angle X-ray scattering

Small angle X-ray scattering (SAXS) experiments were performed on a XEUSS SAXS system (XENOCS SA, France) with an X-ray wavelength 1.5411 Å, a sample to detector distance of 2522 mm, covering a scattering vector from 0.00134 nm⁻¹ to 1.2 nm⁻¹ at room temperature. The average exposure time was 600 s for each scan. The two-dimensional SAXS patterns were converted into one-dimensional data using a Fit2D software.

Differential scanning calorimetry

Glass transition temperature (T_g) of samples was determined by differential scanning calorimetry (DSC) on the second-run heat-flow curve measured on a differential scanning calorimeter (Q100, TA, USA) during heating the samples from 40 °C to 230 °C at a rate of 10 °C min⁻¹ under a nitrogen flow of 50 mL min⁻¹.

Rheology measurement

Rheological measurements of hot-pressed disc samples of 25 mm diameter and 1 mm in the thickness were conducted using an advance rheometric expansion system (ARES-G2, TA, USA) with 25 mm parallel plate geometry. Dynamic frequency (ω) sweeps were performed from 0.0159 rad s⁻¹ to 100 rad s⁻¹ at temperature from 160 °C to 220 °C under 1% strain amplitude in the linearity regime.

Broadband dielectric study

Broadband dielectric spectroscopy (BDS) was measured on a Novocontrol Alpha high resolution dielectric analyzer (Novocontrol GmbH Concept 40, Novocontrol Technology, Germany). Sample films of 0.1–0.2 mm in thickness were sandwiched between two gold electrodes of 20 mm in diameter. Isothermal relaxation spectra were recorded over a frequency (f) range from 10⁻¹ Hz to 10⁷ Hz at temperatures from −40 °C to 160 °C. Several dielectric relaxation parameters were obtained by fitting complex permittivity (ε*) to the Havriliak–Negami (HN) equation⁶²where Δε = ε₀ − ε_∞ is dielectric strength, ε₀ and ε_∞ are dielectric constants at limiting high and low frequencies, respectively. ω (=2πf) is angular frequency. α_HN and β_HN (0 < α_HN < 1, α_HNβ_HN ≤ 1) are relaxation shape parameters, indicative of the breadth of the relaxation and the peak asymmetry (in log form), respectively. σ is DC conductivity, and the coefficient s (0 < s ≤ 1) characterizes the nature of the conduction process. The characteristic relaxation time τ_HN is related to the time of maximum loss (τ_max) by:

Results and discussions

Characterization of structure and morphology

FTIR spectra of PMMA, PMMH and the ionomers are shown in Fig. 1(a). In order to clearly observe the absorption bands in PMMH and ionomers that are covered by the strong bands from PMMA, the spectrum of PMMA is subtracted from those of other samples⁶³ and the resolving curves after spectral subtraction are shown in Fig. 1(b) in the 1300–1800 cm⁻¹ range. The band at 1700 cm⁻¹ in PMMH and PMMA-40% La is attributed to ν(C=O) of carboxylic acid dimer,⁶⁴ suggesting the formation of hydrogen bonds. This band disappears in PMMA-80% La and PMMA-120% La, suggesting the carboxylic acid groups mainly participate in coordination with La(III) cations. The symmetrical carboxylate stretching, ν_s(COO⁻), is located at 1435 cm⁻¹. A new broad band near 1545 cm⁻¹ assigned to the asymmetrical carboxylate stretching, ν_as(COO⁻), appears in the ionomers. The wavenumber difference ν_as − ν_s = 110 cm⁻¹ reveals that the coordination state of carboxylate is bidentate chelating or bidentate bridging rather than monodentate (ν_as − ν_s > 200 cm⁻¹).⁶⁵ The ν(C=O) band disappears and the ν_as(COO⁻) band becomes strong with increasing neutralization level, indicating the formation of coordination structure⁵⁹ of bidentate chelating lanthanum carboxylate⁶⁶ with a coordination number of 8–9 or greater according to a model study of the carboxylate band in lanthanum acetate.⁶⁷

Fig. 1 (a) FTIR spectra of PMMA, PMMH and ionomers; (b) the resolving curves of PMMH and ionomers by subtracting the spectrum of PMMA in the range of 1300–1800 cm⁻¹.

Fig. 2 compares SAXS profiles of PMMA, PMMH and the ionomers at room temperature. An upturn is found for all the ionomers in the low scattering vector q region due to an inhomogeneous spatial distribution of ionic multiplets and/or aggregates.^61,68 The upturn for PMMA is due to spill from the beamstop.⁶⁹ No characteristic peak of “ionic aggregates” is found in PMMH and ionomers except for PMMA-120% La that exhibits a scattering shoulder at q ≈ 0.17 nm⁻¹ with a Bragg space about 37 nm, indicating existence of ionic aggregates¹³ coexisting with multiplets.^7,8 It should be noted that this aggregate structure is not the “cluster phase” defined by Eisenberg et al.,¹⁴ which is confirmed by a single T_g observed in DSC and BDS tests.

Fig. 2 SAXS data of PMMA, PMMH and ionomers.

Ionic effects on segmental dynamics of ionomers

BDS is frequently used to elaborate the ionic effects on segmental and local motions as well as aggregate dynamics.⁶⁹ Fig. 3(a) shows frequency (f) dependence of normalized dielectric loss (ε′′/ε′′_max) spectra for PMMA, PMMH and the ionomers at 353 K (below T_g) and 390 K (above T_g), respectively. To quantitatively analyze the dielectric spectra, they are fitted with eqn (1) and a representative sample is shown in Fig. 3(b). Two HN equations and a conductivity term are used to analyze the spectra above T_g, and a single HN equation could well describe the data below T_g. The relaxation times (τ_max) of α and β relaxations in the measured f window are shown in Fig. 3(c). The local β relaxation involved in rotation of methoxycarbonyl (–COOCH₃) side group about C–C bond remains unchanged regardless of the neutralization level. τ_max as a function of temperature (T) follows the Arrhenius law with an apparent activation energy of 78.2 ± 2.5 kJ mol⁻¹ and 90.5 ± 6.1 kJ mol⁻¹ at temperature below and above the calorimetric T_g, respectively. The former is consistent with the literature data⁷⁰ and the latter of higher value is due to cooperativity of β and α relaxations.⁷¹ The τ_max of α relaxation is well described by Vogel–Fulcher–Tammann (VFT) equationwhere T₀ is Vogel temperature, τ₀ is a characteristic time associated with vibration lifetimes, and the parameter B is related to apparent activation energy and fragility. The fitted parameters are listed in Table 1. T_g(BDS) is estimated as the temperature at τ_max = 0.1 s for the α relaxation,^72,73 which is slightly higher than that determined by DSC at 10 °C min⁻¹.

Fig. 3 (a) Frequency (f) dependences of normalized dielectric loss (ε′′/ε′′_max) spectra of PMMA, PMMH and the ionomers at 353 K and 390 K; (b) a representative sample fitted with HN equations; and (c) relaxation times (τ_max) of the α and β processes. Inset in (a) shows parameters α_HN and α_HNβ_HN of α relaxation at 390 K according to HN fittings. Inset in (c) shows τ_max of α relaxation against T_g(BDS)/T. In (b), the solid curve is the cumulative curve and the dashed ones represent the contributions of α and β processes and the conductivity, respectively. In (c), the curves represent the VFT fits for α relaxation and the Arrhenius fits for β relaxation.

Table 1 Parameters of VFT equation for α process and calorimetric T_g of PMMA, PMMH and ionomers

Sample	log(τ0/s)	B	T0/K	Tg(BDS) ± 1 K	Tg(DSC) ± 1 K	m ± 3
PMMA	−6.3 ± 0.9	87.8 ± 46.0	357.5 ± 6.2	374.1	368.0	51.8
PMMH	−7.7 ± 0.9	128.4 ± 51.7	358.1 ± 5.2	377.3	371.1	56.6
PMMA-40% La	−10.9 ± 0.7	387.0 ± 68.5	340.3 ± 3.9	379.4	373.4	41.6
PMMA-80% La	−10.2 ± 2.6	349.2 ± 51.0	341.9 ± 7.6	381.0	376.1	39.8
PMMA-120% La	−7.8 ± 0.5	137.4 ± 25.9	362.1 ± 2.1	382.3	377.5	55.7

---

Both the α relaxation time and T_g vary with the molecular modifications. As seen in Fig. 3(c) and Table 1, α relaxation time and T_g of PMMH and ionomers are higher than those of PMMA and they increase with neutralization level. The shape parameters α_HN and α_HNβ_HN describe dielectric responses in the low- and high-f limits, respectively.^74,75 While α_HN is related to the intermolecular correlation of the different chains and segments, α_HNβ_HN is related to the local chain dynamics at the glass transition. As shown in inset of Fig. 3(a), α_HNβ_HN at 390 K increases slightly while α_HN decreases notably with introducing hydrogen bonding and/or ionic associations. For PMMA at 344 K, the fitting gives rise to α_HN = 0.55 ± 0.03 and α_HNβ_HN = 0.16 ± 0.04, being consistent with the results reported by Kremer and Schonhals⁷⁶ within the error range and validating the fitting procedure. As shown in inset of Fig. 3(c), τ_max of α relaxation as a function of T_g/T does not overlap. These suggest hindered segmental dynamics in PMMH and ionomers in comparison with PMMA, which are accompanied with increased intermolecular correlation and broadened distribution of relaxation time⁷⁷ due to a wider variety of local environments.⁷⁸

Increasing the neutralization level of ionomers with proper acid contents may influence the ionomer dynamics^20,25 by increasingly longer stringy aggregates and eventually percolated network.⁷⁹ Differring from Na(I)-neutralized ones owning cluster phase^15,80,81 accompanied with splitting of β transition and elevations of the two α and two β transition temperatures,¹⁵ the La(III)-neutralized ionomers with a neutralization level of 80% or below is similar to Cs(I)-neutralized ones that do not contain large scattering centers below 50 nm (ref. 82 and 83) and exhibit a single matrix T_g.⁸⁴ These phenomena suggest that the ionic groups associate into multiplets in the ionomers with a neutralization level of 80% or below. On the other hand, isolated ionic aggregates rather than a rigid “cluster phase”^{2,15,20,24,85} are formed in PMMA-120% La, though the multiplets and aggregates become increasingly ionic with increasing neutralization level.²⁰ In this case, the matrix T_g increasing with neutralization level is affected by segments in proximity to ionic multiplets, instead of multiplets themselves.¹¹

Dynamic fragility (m), referring to deviations from Arrhenius temperature dependence of α relaxation,⁸⁶ is widely used to study dynamics of macromolecules and can be defined from the VFT parameters according to

m governs breadth of glass formation and is controlled by the chain packing ability^87–89 and interactions.^90,91 The values of m are also listed in Table 1. Following the general trend that m and T_g vary proportionally in a variety of glass forming polymers and hydrogen bonding organic liquids,⁸⁶ PMMH has m and T_g values (m = 56.6, T_g = 377.3 K) higher than those of PMMA (m = 51.8, T_g = 374.1 K), which is ascribed to improved backbone stiffness^90,92 by intermolecular hydrogen bonding between polar acid groups.^72,73,93 Being similar to poly(ethylene oxide)-based single-ion conductor⁹⁴ and ion-irradiated poly(ether ether ketone),⁹⁵ the ionomers PMMA-40% La and PMMA-80% La have higher T_g but lower m values and exhibit an unexpected “stronger” behavior than PMMA and PMMH. In these subneutralized ionomers, unneutralized acid groups may form dimers or associate with neutralized complexes.⁹⁶ Thus direct ionic association between carboxylates in the polymer and cations is accompanied with additional hydrogen bonding between acid proton and oxygen.^23,97 The connection of ionic domains by a hydrogen-bonded network²³ should be responsible for the strongly coupled segmental dynamics.⁹⁰ Accordingly, the abnormal behavior may be related to the improved intermolecular interactions resulting in the better chains packing efficiency. For the overneutralized ionomers PMMA-120% La, the ionic associations further restrict the mobility of surrounding chains and thus reduce flexibility of the backbone, resulting in higher values of T_g and m.

Linear dynamic rheology of ionomers

Ionic associations strongly affect viscoelasticity of ionomers based on entangled polymers due to the introduction of an additional elastic mechanism arising from physically crosslinked ion aggregates.^53,98 Fig. 4(a) shows master curves of storage and loss moduli (G′ and G′′) constructed by time–temperature superposition (TTS) principle at a reference temperature of 180 °C for all samples. Both PMMH and ionomers exhibit shift factor a_T (shown in Fig. S2†) same as that of PMMA, following Williams–Landel–Ferry equation. In previously studies, the TTS principle is applicable to polystyrene ionomers with sodium methacrylate up to 6 mol% but fails at high ion contents where micro-phase separation introduces additional relaxation mechanisms.⁷⁷ In general, the breakdown of TTS arises in ionomers that possess of multiple relaxation mechanisms with different temperature dependences.^35,44 Thus the good superposition reveals that the PMMA ionomers are thermorheologically simple, which could be ascribed to ion-hopping time lying outside the experimental window.⁹⁹

Fig. 4 Master curves of (a) storage (G′, solid symbol) and loss moduli (G′′, hollow symbol), (b) Cole–Cole curves, (c) complex viscosity (η*, solid symbol) and tan δ (hollow symbol) versus frequency (ω), and (d) normalized relaxation spectra for PMMA, PMMH and ionomers at 180 °C. The data measured at temperatures from 160 °C to 220 °C are superposed to create the master curves in (a) following the TTS principle. Inset in (b) shows amplification drawings of PMMA and PMMH. Inset in (d) shows the longest relaxation time τ₀. In (a), the solid curves are drawn according to the modified two-phase model and the dashed curves indicate the classic terminal flow law.

PMMA, PMMH and PMMA-40% La exhibit a classical terminal response characterized by G′ ∝ ω² and G′′ ∝ ω. It seems that the hydrogen bonding in PMMH and ionic association in PMMA-40% La are too transient to form stable crosslinks.¹⁰⁰ As neutralization level is increased, formation of ionic aggregates^43,101–104 causes G′ and G′′ to deviate from the terminal behavior. PMMA-120% La even behaves gel-like (G′ = G′′ in the low-ω region) with a power law exponent 0.66 for the ω-dependent G′ at low frequencies, pointing to a critical percolation known as the Ginzburg point.⁴² This power law exponent corresponds to a fractal dimension 2.5 for the ionomer network. The overneutralized ionomer exhibits higher viscosity than those neutralized below the stoichiometric quantity, which has also been observed in polydimethylsiloxane ionomers and is explained by the increase of the number of effective crosslinkings.¹⁰⁵

The Cole–Cole plot is sensitive to molecular modifications.¹⁰⁶ Fig. 4(b) shows Cole–Cole plot of loss viscosity η′′ versus storage viscosity η′ at 180 °C. The η′′–η′ plots of PMMA and PMMH are close to semicircle representing a homogeneous phase structure. However, the ionomers PMMA-40% La, PMMA-80% La, and PMMH-120% La exhibit a high-viscosity (low-ω) tail, corresponding to a long-term relaxation mechanism most likely ascribed to the dynamics of ionic aggregates, which becomes more evident with increasing neutralization level.

Fig. 4(c) shows complex viscosity η* and tan δ versus ω. It can be observed that PMMA, PMMH and PMMA-40wt% La exhibit nearly constant η* at low frequencies as well as a sustained decay of tan δ against ω. The ionomers exhibit non-Newtonian behavior at low frequencies and PMMA-80% La and PMMA-120% La demonstrate a tan δ peak, indicating a fluid-to-solid like rheological transition (i.e. physical gelation)^107–109 ascribed to the development of 3D network of dispersed ionic aggregates.^103,110 Besides, the friction imposed by the supramolecular assemblies act like physical constraints of entanglements and elevate η*. Hence η* at the high-ω side may also change as the neutralization level increases.

The relaxation time spectra H(τ) as a function of relaxation time τ were calculated from dynamic modulus according to Tschoegl.¹¹¹ Fig. 4(d) shows H(τ)τ/τ₀ against τ/τ₀, where τ₀ is determined by the value of η′′ maximum on plot of |η*(ω)| against ω. It is found that the linear rheology of PMMA, PMMH and PMMA-40% La is dominated by one relaxation process though it is prolonged with introducing intermolecular hydrogen bonding and ionic association. Besides, PMMA-80% La and PMMA-120% La display a marked long-term relaxation process that well depicts the Cole–Cole tails [Fig. 4(b)] and the tan δ peaks [Fig. 4(c)].

As shown in Fig. 4(c) and the inset in Fig. 4(d), both η* and τ₀ of PMMH are higher than those of PMMA, which could be ascribed to carboxylic acid dimers and their long-lifetime dimer assembles^112–114 driven by unfavorable interaction between highly polar acid groups and low-polarity polymer medium. Segregation of carboxylic acid groups into polar domains like multiplets^115,116 makes PMMH with a low acid content (2.50 mol%) behave as a weakly interacting hydrogen-bond forming polymer¹¹⁷ with slightly improved dynamic moduli at frequencies below the inverse reptation time.¹¹⁸ In comparison with PMMH, the ionomer PMMA-40% exhibits slightly lowered η* and notably raised τ₀. Being similar to subneutralized poly(ethylene-methacrylic acid),¹¹⁹ the excess acid groups in PMMA-40% La may interact preferentially with the ionic units and plasticize the ionic multiplets thus lower η*. However, the intermolecular associations created by the ionic multiplets tend to retard the segmental relaxation and chain diffusion.⁷⁷ Furthermore, both η* and τ₀ increase with increasing neutralization level, which is ascribed to the rigid multiplets acting as both physical crosslinks and ultrafine particles in the matrix.^120,121 The nonterminal behaviors of PMMA-80% La and PMMA-120% La strongly indicate the presence of a network structure.^39,122 The longer relaxation times are responsible for the higher viscosities of the ionomer compared with PMMA.⁹⁸ It seems that there is a critical neutralization level¹⁰ that controls the number of multiplets and the number of ion pairs per multiplet¹²³ for the network formation. Previous investigations reveal a critical neutralization level ranging from 35% to 80% required for polyethylene,^33,34 poly(ethyl acrylate)¹²³ and polystyrene-based ionomers¹²³ to act as biphasic materials. However, in the ionomers based on low-carboxylated PMMA, the fluid-to-solid transition with increasing neutralization level is not related to percolation of the “cluster phase”. On the other hand, it is involved in the network formation by multiplets and their dynamically restricted nearby chain segments forming hydrocarbon layer surrounding the ionic cores.^{8,18,31,124,125} The bridging chains with their two ends participating in the hydrocarbon layers belonging to different multiplets (and aggregates in PMMA-120% La) are thus important for the network formation.

Gelation mechanism based on “two phase” model

The ionomers with low ion contents can be treated as a system of rigid fillers (ionic multiplets) in a soft continuous phase.^40,53,54 It is worthy of interpreting the ionomer rheology within the framework of filler reinforcement theories. Considering that the isolated ionic multiplets or aggregates carrying a thin layer of immobilized nonionic hydrocarbon segments as the “filler phase”, the stress carried by the trapped segments between ionic domains gives rise to a low-ω second plateau.¹¹⁴ The linear rheology might be discussed applying a “two phase” model originally proposed by Leonov¹²⁶ who attempts to separate a viscoelastic stress arising from micro-flow of the matrix around rigid flocs, and another stress due to attractive nanoparticles dispersed in the matrix. Linear dynamic modulus of the ionomer melts, G*(ω, φ), is divided into two contributions: from the matrix and from the filler networkwhich is applicable for a variety of filled polymers.^127–137 Here the ω-independent parameter A_f(φ) accounts for amplified strain of interstitial fluid.¹³⁸ The Leonov model could be simplified, when ignoring the stress contribution of the rigid flocs, to the prediction of continuum theories¹³⁹for perfectly bonded inclusion–polymer interface. A scaling approximation¹²⁹is proposed for accounting for viscoelasticity of the “filler phase”. Here, R′_f(φ) and R′′_f(φ) are scaling factors representing the elastic and viscous contributions of the “filler phase” and the exponent n defines the liquid- (n = 1) to solid-like (n = 0) transition.

At temperatures where the lifetime of the ionic domains inside matrix is longer than the longest Rouse relaxation time of the chain, alteration of the segmental dynamics is expected.¹¹⁴ Therefore, eqn (5a), (6a) and (7a), respectively, are modified as

These three equations are used to fit G*(ω, φ) and the best fitting results are shown in Fig. 4(a) as solid curves. It is found that eqn (6b) well describes the linear rheology of PMMH and PMMA-40% La, suggesting the ionic multiplets behaving as isolated rigid flocs that retard the polymer diffusion. On the other hand, the linear rheology of PMMA-80% La and PMMA-120% La could be fitted by eqn (5b) and (7b), approving the presence of an interconnected multiplets network that penetrates through the PMMA matrix with retarded chain diffusion. The two-phase model could not account for the friction imposed by the ionic assemblies thus it predicts G*(ω, φ) lower than the measured data at high frequencies. The strain amplification factor A_f(φ) is determined as 1.0 for PMMH and 0.4, 1.2, and 1.5, respectively, PMMA-80% La and PMMA-120% La, which could approximately account for the variations of G*(ω, φ) with respect to molecular modification. The scaling exponent n is determined as 0.4 and 0.2, respectively, for PMMA-80% La and PMMA-120% La, being in connection with increased connectivity of multiplets in the network with increasing neutralization level. Furthermore, R′_f(φ) and R′′_f(φ) are determined as 40 and 8 Pa¹⁻ⁿ, respectively, for PMMA-80% La and the values are 500 and 0.5 Pa¹⁻ⁿ for PMMA-120% La, suggesting that the supramolecular assemblies at high neutralization levels greatly improve the elasticity and depress the viscous components of the network. This could be assigned to generation of multiple ionic aggregates interconnected by bridging chains.

Conclusions

The molecular dynamics and dynamic rheology of PMMA-based La(III) ionomers with varying neutralization levels have been studied. The α relaxation is slowed down and the matrix T_g is elevated with increasing neutralization level. The creation of rheological TTS master curves of G*(ω) reveals stable ionic structures in the temperature range from 160 °C to 220 °C. The Cole–Cole, η*(ω), tan δ versus ω and H(τ)τ/τ₀ versus τ/τ₀ plots, all collapsed in the high-ω region, suggest that there are two kinds of ionic structures formed in the matrix: isolated ionic multiplets in PMMA-40% La and interconnected multiplets network in PMMA-80% La and PMMA-120% La. The identification of the interconnected multiplets network provides a new mechanism for understanding the fluid-to-solid transition of “cluster phase”-free ionomers with increasing neutralization level.

Acknowledgements

This work was supported by the National Natural Science Foundation of Zhejiang Province (Grant No. R14E030003), the National Natural Science Foundation of China (Grant No. 51573157, 51333004, and 51373149), and the Major Projects of Science and Technology Plan of Guizhou Province (Grant No. (2013) 6016).

Notes and references

1. L. Zhang, N. R. Brostowitz, K. A. Cavicchi and R. A. Weiss, Macromol. React. Eng., 2014, 8, 81–99.
2. K. H. Ko and J. S. Kim, Kirk-Othmer Encyclopedia of Chemical Technology, 1998.
3. Y. Shi and R. A. Weiss, Macromolecules, 2014, 47, 1732–1740.
4. A. Agrawal, D. Perahia and G. S. Grest, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 022601.
5. Q. Chen, G. J. Tudryn and R. H. Colby, J. Rheol., 2013, 57, 1441–1462.
6. W. Wang, G. J. Tudryn, R. H. Colby and K. I. Winey, J. Am. Chem. Soc., 2011, 133, 10826–10831.
7. A. Batra, C. Cohen, H. Kim, K. I. Winey, N. Ando and S. M. Gruner, Macromolecules, 2006, 39, 1630–1638.
8. A. Taubert and K. I. Winey, Macromolecules, 2002, 35, 7419–7426.
9. Y. Liu, J. L. Horan, G. J. Schlichting, B. R. Caire, M. W. Liberatore, S. J. Hamrock, G. M. Haugen, M. A. Yandrasits, S. Seifert and A. M. Herring, Macromolecules, 2012, 45, 7495–7503.
10. J. H. Laurer and K. I. Winey, Macromolecules, 1998, 31, 9106–9108.
11. Y. Jia, A. Kleinhammes and Y. Wu, Macromolecules, 2005, 38, 2781–2785.
12. V. Farrell and P. Grady, Macromolecules, 2001, 34, 7108–7112.
13. S.-I. Han, S. S. Im and D. K. Kim, Polymer, 2003, 44, 7165–7173.
14. A. Eisenberg, B. Hird and R. B. Moore, Macromolecules, 1990, 23, 4098–4107.
15. X. Ma, J. A. Sauer and M. Hara, Macromolecules, 1995, 28, 3953–3962.
16. S. A. Visser and S. L. Cooper, Macromolecules, 1992, 25, 2230–2236.
17. D. J. Yarusso and S. L. Cooper, Macromolecules, 1983, 16, 1871–1880.
18. N. M. Benetatos, C. D. Chan and K. I. Winey, Macromolecules, 2007, 40, 1081–1088.
19. Y. Tsujita, M. Yasuda, M. Takei, T. Kinoshita, A. Takizawa and H. Yoshimizu, Macromolecules, 2001, 34, 2220–2224.
20. A. M. Castagna, W. Wang, K. I. Winey and J. Runt, Macromolecules, 2011, 44, 2791–2798.
21. C. F. Buitrago, D. S. Bolintineanu, M. E. Seitz, K. L. Opper, K. B. Wagener, M. J. Stevens, A. L. Frischknecht and K. I. Winey, Macromolecules, 2015, 48, 1210–1220.
22. C. F. Buitrago, T. M. Alam, K. L. Opper, B. S. Aitken, K. B. Wagener and K. I. Winey, Macromolecules, 2013, 46, 8995–9002.
23. D. S. Bolintineanu, M. J. Stevens and A. L. Frischknecht, Macromolecules, 2013, 46, 5381–5392.
24. S.-H. Kim and J.-S. Kim, Macromolecules, 2003, 36, 2382–2386.
25. J.-S. Kim and A. Eisenberg, J. Polym. Sci., Part B: Polym. Phys., 1995, 33, 197–209.
26. M. Goswami, J. M. Borreguero and B. G. Sumpter, J. Chem. Phys., 2015, 142, 084903.
27. N. M. Benetatos and K. I. Winey, Macromolecules, 2007, 40, 3223–3228.
28. J.-S. Kim, Y. Hwa Nah and S.-S. Jarng, Polymer, 2001, 42, 5567–5571.
29. J. S. Kim, Y. H. Nah, S. S. Jarng, W. Kim, Y. Lee and Y. W. Kim, Polymer, 2000, 41, 3099–3102.
30. D. Duchesne and A. Eisenberg, Can. J. Chem., 1990, 68, 1228–1232.
31. M. E. L. Wouters, J. G. P. Goossens and F. L. Binsbergen, Macromolecules, 2002, 35, 208–216.
32. M. E. L. Wouters, V. M. Litvinov, F. L. Binsbergen, J. G. P. Goossens, M. van Duin and H. G. Dikland, Macromolecules, 2003, 36, 1147–1156.
33. E. Hirasawa, Y. Yamamoto, K. Tadano and S. Yano, J. Appl. Polym. Sci., 1991, 42, 351–362.
34. H. Tachino, H. Hara, E. Hirasawa, S. Kutsumizu, K. Tadano and S. Yano, Macromolecules, 1993, 26, 752–757.
35. N. K. Tierney and R. A. Register, Macromolecules, 2003, 36, 1170–1177.
36. P. Atorngitjawat, R. J. Klein and J. Runt, Macromolecules, 2006, 39, 1815–1820.
37. S. Kutsumizu, H. Tagawa, Y. Muroga and S. Yano, Macromolecules, 2000, 33, 3818–3827.
38. M. E. Seitz, C. D. Chan, K. L. Opper, T. W. Baughman, K. B. Wagener and K. I. Winey, J. Am. Chem. Soc., 2010, 132, 8165–8174.
39. F. Dalmas and E. Leroy, Macromolecules, 2011, 44, 8093–8099.
40. K. H. Ko, M. Luqman, Y. W. Kim and J. S. Kim, J. Polym. Sci., Part B: Polym. Phys., 2016, 54, 1043–1053.
41. S. Kutsumizu, K. Tadano, Y. Matsuda, M. Goto, H. Tachino, H. Hara, E. Hirasawa, H. Tagawa, Y. Muroga and S. Yano, Macromolecules, 2000, 33, 9044–9053.
42. Q. Chen, C. Huang, R. A. Weiss and R. H. Colby, Macromolecules, 2015, 48, 1221–1230.
43. Q. Chen and R. H. Colby, Korea Aust. Rheol. J., 2014, 26, 257–261.
44. G. H. Ling, Y. Wang and R. A. Weiss, Macromolecules, 2012, 45, 481–490.
45. R. A. Weiss and H. Zhao, J. Rheol., 2009, 53, 191–213.
46. X. Qiao and R. A. Weiss, Macromolecules, 2013, 46, 2417–2424.
47. R. H. Colby, X. Zheng, M. H. Rafailovich, J. Sokolov, D. G. Peiffer, S. A. Schwarz, Y. Strzhemechny and D. Nguyen, Phys. Rev. Lett., 1998, 81, 3876–3879.
48. R. Stadler and L. De Lucca Freitas, Macromolecules, 1989, 22, 714–719.
49. L. Leibler, M. Rubinstein and R. H. Colby, Macromolecules, 1991, 24, 4701–4707.
50. M. Rubinstein and A. N. Semenov, Macromolecules, 2001, 34, 1058–1068.
51. M. Ahmadi, L. G. D. Hawke, H. Goldansaz and E. van Ruymbeke, Macromolecules, 2015, 48, 7300–7310.
52. Q. Chen, S. Liang, H.-s. Shiau and R. H. Colby, ACS Macro Lett., 2013, 2, 970–974.
53. J.-S. Kim, R. J. Jackman and A. Eisenberg, Macromolecules, 1994, 27, 2789–2803.
54. M. Nishida and A. Eisenberg, Macromolecules, 1996, 29, 1507–1515.
55. L. M. Hall, M. J. Stevens and A. L. Frischknecht, Macromolecules, 2012, 45, 8097–8108.
56. N. K. Tierney, S. T. Trzaska and R. A. Register, Macromolecules, 2004, 37, 10205–10207.
57. M. Nishio, A. Nishioka, T. Taniguchi and K. Koyama, Polymer, 2005, 46, 261–266.
58. K. Tadano, E. Hirasawa, H. Yamamoto and S. Yano, Macromolecules, 1989, 22, 226–233.
59. K. Han and H. L. Williams, J. Appl. Polym. Sci., 1991, 42, 1845–1859.
60. M. W. Spencer, M. D. Wetzel, C. Troeltzsch and D. R. Paul, Polymer, 2012, 53, 569–580.
61. R. A. Register and S. L. Cooper, Macromolecules, 1990, 12, 310–317.
62. S. Havriliak and S. Negami, J. Polym. Sci., Part C: Polym. Symp., 1966, 14, 99–117.
63. Q. Chen, H. Masser, H.-S. Shiau, S. Liang, J. Runt, P. C. Painter and R. H. Colby, Macromolecules, 2014, 47, 3635–3644.
64. Y. Gotoh, J. Imakita, Y. Ohkoshi and M. Nagura, Polym. J., 2000, 32, 838–844.
65. Y. Gotoh, Y. Ohkoshi and M. Nagura, Polym. J., 2004, 36, 255–260.
66. G. B. Deacon and R. J. Phillips, Coord. Chem. Rev., 1980, 33, 227–250.
67. D. G. Karraker, J. Inorg. Nucl. Chem., 1969, 31, 2815–2832.
68. X. Lu and R. A. Weiss, Macromolecules, 1992, 25, 6185–6189.
69. P. Atorngitjawat and J. Runt, Macromolecules, 2007, 40, 991–996.
70. R. Bergman, F. Alvarez, A. Alegría and J. Colmenero, J. Chem. Phys., 1998, 109, 7546–7555.
71. F. Garwe, A. Schönhals, H. Lockwenz, M. Beiner, K. Schröter and E. Donth, Macromolecules, 1996, 29, 247–253.
72. S. Zhang, P. C. Painter and J. Runt, Macromolecules, 2002, 35, 9403–9413.
73. B. D. Fitz and J. Mijovic, Macromolecules, 1999, 32, 3518–3527.
74. E. Schlosser and A. Schönhals, Colloid Polym. Sci., 1989, 267, 963–969.
75. A. Schönhals and E. Schlosser, Colloid Polym. Sci., 1898, 267, 125–132.
76. A. Schönhals and F. Kremer, in Broadband dielectric spectroscopy, Springer, 2003, pp. 59–98.
77. A. Eisenberg and M. Navratil, Macromolecules, 1973, 6, 604–612.
78. J. Bartels, J.-H. H. Wang, Q. Chen, J. Runt and R. H. Colby, Macromolecules, 2016, 49, 1903–1910.
79. D. S. Bolintineanu, M. J. Stevens and A. L. Frischknecht, ACS Macro Lett., 2013, 2, 206–210.
80. Y.-H. Nah, J.-S. Kim, B.-W. Jo, J. Kim and Y. Lee, Polym. Bull., 1999, 42, 213–219.
81. A. R. Lim and J. S. Kim, Solid State Commun., 2000, 115, 179–183.
82. J.-S. Kim and A. Eisenberg, Polym. J., 1999, 31, 303–305.
83. M. Jiang, A. A. Gronowski, H. L. Yeager, G. Wu, J. S. Kim and A. Eisenberg, Macromolecules, 1994, 27, 6541–6550.
84. A. A. Gronowski, M. Jiang, H. L. Yeager, G. Wu and A. Eisenberg, J. Membr. Sci., 1993, 82, 83–97.
85. B. P. Grady, Polym. Eng. Sci., 2008, 48, 1029–1051.
86. Q. Qin and G. B. McKenna, J. Non-Cryst. Solids, 2006, 352, 2977–2985.
87. J. Dudowicz, K. F. Freed and J. F. Douglas, J. Phys. Chem. B, 2005, 109, 21285–21292.
88. J. Dudowicz, K. F. Freed and J. F. Douglas, J. Phys. Chem. B, 2005, 109, 21350–21356.
89. J. Dudowicz, K. F. Freed and J. F. Douglas, J. Chem. Phys., 2006, 124, 064901.
90. A. L. Agapov, Y. Wang, K. Kunal, C. G. Robertson and A. P. Sokolov, Macromolecules, 2012, 45, 8430–8437.
91. W.-S. Xu and K. F. Freed, Macromolecules, 2014, 47, 6990–6997.
92. E. B. Stukalin, J. F. Douglas and K. F. Freed, J. Chem. Phys., 2009, 131, 114905.
93. K. L. Ngai and C. M. Roland, Macromolecules, 1993, 26, 6824–6830.
94. D. Fragiadakis, S. Dou, R. H. Colby and J. Runt, J. Chem. Phys., 2009, 130, 064907.
95. A. G. Al Lafi, J. Appl. Polym. Sci., 2014, 131, 39929.
96. R. M. Walters, K. E. Sohn, K. I. Winey and R. J. Composto, J. Polym. Sci., Part B: Polym. Phys., 2002, 40, 2833–2841.
97. T. M. Alam, J. E. Jenkins, D. S. Bolintineanu, M. J. Stevens, A. L. Frischknecht, C. F. Buitrago, K. I. Winey, K. L. Opper and K. B. Wagener, Materials, 2012, 5, 1508–1527.
98. R. A. Weiss, J. J. Fitzgerald and D. Kim, Macromolecules, 1991, 24, 1071–1076.
99. P. Vanhoorne and R. A. Register, Macromolecules, 1996, 29, 598–604.
100. M. Navratil and A. Eisenberg, Macromolecules, 1974, 7, 84–89.
101. K. Wakabayashi and R. A. Register, Macromolecules, 2006, 39, 1079–1086.
102. P. Akcora, S. K. Kumar, J. Moll, S. Lewis, L. S. Schadler, Y. Li, B. C. Benicewicz, A. Sandy, S. Narayanan, J. Ilavsky, P. Thiyagarajan, R. H. Colby and J. F. Douglas, Macromolecules, 2010, 43, 1003–1010.
103. M. Joshi, B. S. Butola, G. Simon and N. Kukaleva, Macromolecules, 2006, 39, 1839–1849.
104. Y. Song and Q. Zheng, J. Rheol., 2015, 59, 155–191.
105. A. Batra, C. Cohen and T. M. Duncan, Macromolecules, 2006, 39, 426–438.
106. P. He, W. Shen, W. Yu and C. Zhou, Macromolecules, 2014, 47, 807–820.
107. B. X. Fu, M. Y. Gelfer, B. S. Hsiao, S. Phillips, B. Viers, R. Blanski and P. Ruth, Polymer, 2003, 44, 1499–1506.
108. H. H. Winter and F. Chambon, J. Rheol., 1986, 30, 367–382.
109. Y. Gelfer and H. H. Winter, Macromolecules, 1999, 32, 8974–8981.
110. M. A. Osman and A. Atallah, Polymer, 2006, 47, 2357–2368.
111. N. W. Tschoegl, in The Phenomenological Theory of Linear Viscoelastic Behavior: An Introduction, Springer Berlin Heidelberg, Berlin, Heidelberg, 1989, pp. 157–243,  DOI:10.1007/978-3-642-73602-5_4.
112. C. A. Lueth, D. S. Bolintineanu, M. J. Stevens and A. L. Frischknecht, J. Chem. Phys., 2014, 140, 054902.
113. L. G. D. Hawke, M. Ahmadi, H. Goldansaz and E. van Ruymbeke, J. Rheol., 2016, 60, 297–310.
114. H. Goldansaz, C.-A. Fustin, M. Wübbenhorst and E. van Ruymbeke, Macromolecules, 2016, 49, 1890–1902.
115. H. Klok, E. A. Rebrov, A. M. Muzafarov, W. Michelberger and M. Moller, J. Polym. Sci., Part B: Polym. Phys., 1999, 37, 485–495.
116. L. Z. Rogovia, V. G. Vasil'ev, V. S. Papkov, O. I. Shchegolikhina, G. L. Slonimskii and A. A. Zhdanov, Macromol. Symp., 1995, 93, 135–142.
117. C. L. Lewis, K. Stewart and M. Anthamatten, Macromolecules, 2014, 47, 729–740.
118. A. Shabbir, H. Goldansaz, O. Hassager, E. van Ruymbeke and N. J. Alvarez, Macromolecules, 2015, 48, 5988–5996.
119. N. K. Tierney and R. A. Register, Macromolecules, 2002, 35, 6284–6290.
120. I. Capek, Adv. Colloid Interface Sci., 2005, 118, 73–112.
121. S. A. Visser and S. L. Cooper, Macromolecules, 1991, 24, 2576–2583.
122. B. X. Fu, M. Y. Gelfer, B. S. Hsiao, S. Phillips, B. Viers, R. Blanski and P. Ruth, Polymer, 2003, 44, 1499–1506.
123. S.-H. Kim, Y.-M. Kim, J.-S. Kim and J.-A. Yu, Polym. Bull., 2014, 72, 295–308.
124. Y. Miwa, T. Kondo and S. Kutsumizu, Macromolecules, 2013, 46, 5232–5237.
125. S. Kutsumizu, M. Goto, S. Yano and S. Schlick, Macromolecules, 2002, 35, 6298–6305.
126. A. I. Leonov, J. Rheol., 1990, 34, 1039–1068.
127. Y. Song and Q. Zheng, Polymer, 2010, 51, 3262–3268.
128. Y. Song and Q. Zheng, Polymer, 2011, 52, 593–596.
129. Y. Song and Q. Zheng, Polymer, 2011, 52, 6173–6179.
130. Y. Song and Q. Zheng, Polym. Bull., 2013, 15, 22–34.
131. Y. Song, Q. Zheng and Q. Cao, J. Rheol., 2009, 53, 1379–1388.
132. Y. Song, J. Sun and Q. Zheng, Acta Polym. Sin., 2009, 18, 729–734.
133. Y. Song and Q. Zheng, Acta Polym. Sin., 2012, 21, 1383–1388.
134. Y. Tan, X. Yin, M. Chen, Y. Song and Q. Zheng, J. Rheol., 2011, 55, 965–979.
135. D. Wu, J. Wang, M. Zhang and W. Zhou, Ind. Eng. Chem. Res., 2012, 51, 6705–6713.
136. J. Wang, D. F. Wu, X. Li and M. Zhang, Polym. Eng. Sci., 2013, 53, 2541–2548.
137. G. Y. H. Choong, D. S. A. De Focatiis and D. G. Hassell, Rheol. Acta, 2013, 52, 801–814.
138. A. Lapra, F. Clément, L. Bokobza and L. Monnerie, Rubber Chem. Technol., 2003, 76, 60–81.
139. V. Pryamitsyn and V. Ganesan, Macromolecules, 2006, 39, 844–856.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra10135f

---