Observation of exceptional ‘de Vries-like’ properties in a conventional aroylhydrazone based liquid crystal

Abstract

Smectic liquid crystals with ‘de Vries-like’ properties are characterized by a maximum layer contraction of ≤1% upon transition from the non-tilted SmA phase to the tilted SmC phase. A straight alkoxy chain-terminated conventional aroylhydrazone based liquid crystal N-(4-(tetradecyloxy)-2-hydroxybenzylidene)-4′((4′′(hexadecyloxy)benzyl)oxy)benzohydrazide (BS_ac-1416) undergoes the SmA–SmC phase transition with a maximum layer contraction of 0.65%. The merits of the de Vries reduction factor, i.e. R and f values for this mesogen, are comparable to, or even lower than, those reported for established perfluorinated and polysiloxane-terminated bona fide de Vries-like materials.

---

Smectic A (SmA) and smectic C (SmC) liquid crystals are layered phases possessing quasi-long-range positional order in one dimension represented by a mass-density wave.¹ The wave vector of this density wave is along the director in the case of the SmA phase, while it is tilted in the case of the SmC phase. Owing to this feature, the layer spacing is significantly lower in the tilted SmC phase than in the orthogonal SmA phase.² Maximum layer-shrinkage in a typical SmA–SmC transition can be as high as 11%.^3,4

In 1972, Diele et al. reported a material in which the layer spacing was similar in the SmA and SmC phases.⁵ To explain this feature, de Vries suggested a new type of SmA phase in which the molecules are tilted with respect to the layer normal just as in the SmC phase but the tilt directions of different layers are uncorrelated.⁶ These are now known as the de Vries smectic phases and are characterized by a maximum layer contraction of ≤1% upon transition from the non-tilted SmA phase to the tilted SmC phase.^4,7–15 This phenomenon stems from the diffuse cone model proposed by de Vries that describes the SmA phase as a lamellar structure in which mesogens have a tilted molecular orientation and random azimuthal distribution.¹⁶ According to this idealized model, the SmA–SmC transition is described as an ordering of the azimuthal distribution that results in zero layer contraction, as shown in Fig. 1. The simple reorientation of molecules at the SmA–SmC transition in de Vries-like liquid crystals is advantageous for practical applications. For instance, the low layer contraction avoids the formation of a chevron structure and zigzag defects that usually occur in SmA–SmC transitions of conventional ferroelectric (SmC*) liquid crystals and that are detrimental for the optical quality of electro-optical devices.¹⁷ High electroclinic effects (response, tilt angle, and birefringence) can be achieved at low voltages as compared with typical electroclinic materials on these materials.^18–20

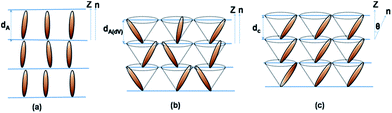Fig. 1 Schematic representation of the molecular arrangement in (a) SmA (b) one type of SmA_dV and (c) SmC phases. The molecules are along the layer normal in the SmA, while being tilted in the SmA_dV and SmC phases. To be noted is the fact that the tilt is azimuthally correlated in the SmC but not in the SmA_dV phase (dV: de Vries).²¹

The structure of this unusual phase has yet to be fully elucidated, but recent theoretical studies suggest that materials combining low orientational order and high lamellar order are likely to exhibit this behavior.^22,23 Three examples of liquid crystal materials known to have very low layer shrinkage and large electroclinic susceptibilities are considered as bona fide ‘de Vries-like’ liquid crystals. These are the siloxane-terminated mesogen TSiKN65 and its carbosilane-terminated analogue W599,^9,24 and the 2-phenylpyrimidine mesogen 3M 8422 with a chiral perfluoroether chain¹⁰ which show maximum layer contractions in the rage of 0.40–0.73% (Fig. 2). In our earlier reports of X-ray, electrical, electro-optical and dielectric studies on such bona fide de Vries LCs, the effect of differential interactions in different molecular end of compounds was found to be one of the major cause of unusual behaviour and minimum layer shrinkage in such systems.^25,26 Rational design strategy and structural investigations of de Vries-like liquid crystals was initiated by Lemieux et al. by design and synthesis of a number of de Vries-like liquid crystals having trisiloxane terminated side-chain materials with 2-phenylpyrimidine core.^27–29 Further, they extended their work by incorporating chemically inert carbosilane-terminated de Vries LCs and substituting the 2-phenylpyrimidine core with the cores known to be stronger ‘SmC-promoters’ in model compounds: 6-phenylpyridazine, 6-phenylpyridine and 2-phenyl thiadiazole.^30,31 In the same reports, drawback of hydrolytical and electrochemical lability of siloxane end group and need of incorporation of chemically inert nanosegregating terminal elements for fabrication of de Vries-like LCs towards electro-optical applications are mentioned.^27,28 Thus, reports on bona fide de Vries-like materials feature nanosegregating structural elements such as siloxane end-groups or perfluorinated side chains and example of simple alkoxy chain-terminated conventional liquid crystal showing de Vries-like properties is still rare. In this communication, we report a structurally unprecedented achiral, chemically inert, straight alkoxy chain-terminated aroylhydrazone based liquid crystal N-(4(tetradecyloxy)-2-hydroxybenzylidene)-4′((4′′(hexadecyloxy)benzyl)oxy)benzohydrazide (BS_ac-1416) showing de Vries like properties comparable to that of perfluorinated or siloxane end-groups containing bona fide de Vries-like liquid crystalline materials.

Fig. 2 Molecular structures of bona fide de Vries-like liquid crystals (TSiKN65, W599, 3M 8422, 2)^8,9,18 and BS_ac-1416.

Compound BS_ac-1416 and initial precursors were obtained by microwave assisted synthetic approach in very good yield (Scheme 1). The detailed experimental procedures and analytical data are described in the ESI.†

Scheme 1 Reactions and reagents: (a) 1-bromohexadecane (30 μL, 0.11 mmol.), Cs₂CO₃ (0.1 g, 0.3 mmol), NMP, MW (150 W), 3–5 min, 87%. (b) LAH, stirring in dry THF at 0 °C, 2 h, 92%. (c) SOCl₂ (0.1 mL, 1.4 mmol), refluxing in dry DCM, DMF (cat.), 20 min, 82%. (d) Cs₂CO₃ (0.49 g, 1.5 mmol), ethyl 4-hydroxybenzoate (0.09 g, 0.5 mmol), 4-hexadecyloxybenzyl chloride (0.18 g, 0.5 mmol), DMF, MW, 70 °C, 2–3 min, 80%. (e) NH₂NH₂·H₂O (0.12 mL, excess), MW, 5–6 min, 82%. (f) 1-Bromotetradecane (0.27 mL, 1.0 mmol), Cs₂CO₃ (1.3 g, 4.0 mmol), NMP, MW (150 W), 3–5 min, 82%. (g) Acetic acid (cat.), EtOH, MW, 5 min, 83%.

The XRD results, microscopic optical observations and differential scanning calorimetry (DSC) enthalpies at the phase transitions have been used to determine mesomorphic properties and de Vries-like behaviour in the newly synthesized compound BS_ac-1416. Accurate measurements of the smectic layer spacing (d) as a function of temperature were carried out by SAXS.

As shown in Fig. 3, the normalized d/d_AC(T) profiles of BS_ac-1416 shows a negative thermal expansion in the SmA phase that persists in the SmC phase and counteracts the layer contraction caused by tilting in the SmC phase. Other bona fide ‘de Vries-like’ materials have been reported to show similar negative thermal expansion in their d(T) profiles.^8,13–15,25 Maximum layer contractions of 0.65% are observed at ca. 10 K below T_AC and the layer spacing at the SmA–SmC transition d_AC is restored upon further cooling to ca. 26.4 K below T_AC.

Fig. 3 Smectic layer spacing versus reduced temperature T − T_AC for compound BS_ac-1416. The dashed lines show the layer spacing at the SmA–SmC transition. The solid lines represent the least-squares fit of the data points in the SmA phase at T − T_AC. The arrows indicate the difference in layer spacing for calculating the R and f reduction factors.

The compound BS_ac-1416 forms SmA and SmC phases. A thin film (18 μm thickness) of the sample observed between crossed polarizers, exhibits the characteristic fan and homeotropic textures of the SmA phase that turn into broken fan texture, upon transition to the SmC phase. In each case, the texture analysis revealed a pronounced change in interference colour on cooling from the isotropic phase to the SmC phase. As shown in Fig. 4, the fan texture shows a green colour just below the clearing point, which gradually turns reddish-green at the SmA–SmC transition point T_AC, and then red at 6 °C below T_AC. The overall colour change corresponds to a net increase in birefringence Δn from ca. 0.07 to 0.08 consistent with an increase in orientational order expected for de Vries-like materials.⁹

Fig. 4 Polarized photomicrographs (20×) of compound BS_ac-1416 in an unaligned glass cell with a spacing of 18 μm during mesophase transitions (from left to right, 176.2, 174.1, 171.8 and 168.2 °C). The change in interference color from (a)–(d) corresponds to an increase in birefringence of ca. 20%.

The optical tilt angle (θ_opt) was measured by polarized optical microscopy (POM) as a function of reduced temperature T − T_AC in the absence of electric field (Fig. 5); θ_opt, obtained as the difference in the angle of rotation between dark states in domains of opposite tilt orientations³⁰ was found to be 26.1°. Its magnitude shows a discontinuity as T approaches T_AC suggesting that the SmA–SmC transition may be weakly first-order in nature. To test this hypothesis, the θ_opt profile was fitted to the power law:

θ ∝ |T − T_c|^β (1)

where β is the order parameter exponent related to the nature of the phase transition and T_c is the critical temperature of a hypothetical second-order transition (i.e., the super-heating limit of the weakly first-order transition).¹ According to the generalized mean-field (Landau) theory of phase transitions, a β value of 0.5 is expected in the case of a pure second-order phase transition, whereas a β value of 0.25 is expected in the case of a transition at the crossover (tricritical) point from second to first-order transition.^32,33 As shown in Fig. 5, fits of the θ_opt profiles to eqn (1) give β value ranging 0.21, which are consistent with the ΔH_AC values measured by DSC and suggest that the SmA–SmC phase transition exhibited by the BS_ac-1416 mesogens reported herein is weakly first-order in nature.⁸

Fig. 5 Optical tilt angle θ_opt versus reduced temperature T − T_AC for the compound BS_ac-1416. The solid lines represent the fits to eqn (1) (β = 0.21).

To assess the potential of a de Vries material to achieve defect-free bookshelf geometry in the SmC phase, Radcliffe et al. defined figures of merit R and f according to eqn (2) and (3):

R = δ(T)/θ_opt(T) = cos⁻¹[d_C(T)/d(T_AC)]/θ_opt(T) (2)

f = θ_Xray(T)/θ_opt(T) = cos⁻¹[d_C(T)/d_A(T)]/θ_opt(T) (3)

Here, assuming a rigid-rod model δ(T) is the tilt angle required to give the observed contraction relative to the layer spacing at the SmA–SmC transition.⁸ In eqn (3), θ_Xray(T), the X-ray tilt required to give the observed layer contraction relative to the SmA layer spacing d_A(T) extrapolated in the SmC phase. This extrapolation is done at a given reduced temperature using least-squares fit of the data points in the SmA phase near the SmA–SmC transition.¹⁰ The latter gives a reduction factor that is normalized with respect to negative thermal expansion. In each equation, the tilt angle derived from layer spacing measurements is divided by the optical tilt angle θ_opt(T) measured by POM. At a reduced temperature T − T_AC = −10 K, θ_Xray observed for BS_ac-1416, is 6.1°, a value consistent with the data for other “de Vries like” materials.¹⁰ The R and f values of this compound at T − T_AC = −10 K were calculated to be 0.23 and 0.44 respectively. Table 1 shows R and f values for the title compound under investigation along with other “de Vries-like” liquid crystals. It is seen that the figures of merit for BS_ac-1416 are comparable to those for the best “de Vries-like” materials reported heretofore, and thus has the potential to achieve defect free bookshelf geometry.⁴

Table 1 Smectic layer spacings, tilt angles, and figures of merit R and f at T − T_AC = −10 K

Cmpds	dC (Å)	dA (Å)	d(TAC) (Å)	θopt (deg)	θXray (deg)	δ (deg)	R	f
a Ref. 18.b Ref. 8.c Ref. 9.
BSac-1416	43.0	43.9	43.3	26.1	6.1	11.4	0.23	0.44
2^a	40.8	43.1	41.2	35	18.8	8.0	0.23	0.54
3M 8422^b	31.7	32.3	31.8	25	11.0	4.5	0.18	0.44
TSiKN65^c	35.70	35.95	35.95	34	6.8	6.8	0.20	0.20

---

In summary, “de Vries-like” liquid crystals behaviour comparable to earlier best reports on such liquid crystals has been observed in a simple straight alkoxy chain-terminated conventional liquid crystal. Ongoing efforts are focused on structure–function relationship studies of homologous series of such mesogens featuring aroylhydrazone core and reduction in melting point of mesogens via structural modifications, and will be reported in due course.

Acknowledgements

HKS (Senior Research Fellow) is grateful to the Council of Scientific and Industrial Research (CSIR), New Delhi, India, for financial support. BS is grateful to DRDO, India (Project No. ERIP/ER/1203053/M/01/1542) and DST, India (Project No. SR/S1/IC-08/2012) for providing financial assistance. S.K.S. is grateful to DST, SERB for providing fellowship under N-PDF (PDF/2015/000147) scheme.

Notes and references

1. S. Chandrasekhar, Liquid Crystals, Cambridge University Press, Cambridge, England, 2nd edn, 1992.
2. C. V. Lobo, S. K. Prasad and D. S. Shankar Rao, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 62701.
3. S. Kumar, Phys. Rev. A: At., Mol., Opt. Phys., 1981, 23, 3207.
4. J. P. Lagerwall and F. Giesselmann, ChemPhysChem, 2006, 7, 20.
5. S. Diele, P. Brand and H. Sackman, Mol. Cryst. Liq. Cryst., 1972, 16, 105.
6. (a) A. De Vries, in Abstracts of the Fifth International Liquid Crystal Conference, Stockholm, ed. G. H. Brown, ILC Society, Kent, OH, 1974, p. 150; (b) A. De Vries, Mol. Cryst. Liq. Cryst., 1977, 41, 27; (c) A. De Vries, A. Ekachai and N. Spielberg, Mol. Cryst. Liq. Cryst., 1979, 49, 143.
7. Y. Takanishi, Y. Ouchi, H. Takezoe, A. Fukuda, A. Mochizuki and M. Nakatsuka, Jpn. J. Appl. Phys., 1990, 2, L984.
8. M. D. Radcliffe, M. L. Brostrom, K. A. Epstein, A. G. Rappaport, B. N. Thomas, R. Shao and N. A. Clark, Liq. Cryst., 1999, 26, 789.
9. M. S. Spector, P. A. Heiney, J. Naciri, B. T. Weslowski, D. B. Holt and R. Shashidhar, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 1579.
10. J. P. F. Lagerwall, F. Giesselmann and M. D. Radcliffe, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 31703.
11. J. Naciri, C. Carboni and A. K. George, Liq. Cryst., 2003, 30, 219.
12. O. E. Panarina, Y. P. Panarin, J. K. Vij, M. S. Spector and R. Shashidhar, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 51709.
13. M. Rossle, R. Zentel, J. P. F. Lagerwall and F. Giesselmann, Liq. Cryst., 2004, 31, 883.
14. N. Hayashi, T. Kato, A. Fukuda, J. K. Vij, Y. P. Panarin, J. Naciri, R. Shashidhar, S. Kawada and S. Kondoh, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 41705.
15. O. E. Panarina, Y. P. Panarin, F. Antonelli, J. K. Vij, M. Reihmann and G. Galli, J. Mater. Chem., 2006, 16, 842.
16. F. Giesselmann, P. Zugenmaier, I. Dierking, S. T. Lagerwall, B. Stebler, M. Kaspar, V. Hamplova and M. Glogarova, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 598.
17. A. de Vries, J. Chem. Phys., 1979, 71, 25.
18. J. C. Roberts, N. Kapernaum, F. Giesselmann and R. P. Lemieux, J. Am. Chem. Soc., 2008, 130, 13842.
19. F. Goc, C. Blanc, V. Lorman, M. Nobili, S. Samaritani, G. Galli and W. Kuczynski, Ferroelectrics, 2006, 343, 101.
20. K. Saunders, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 11703.
21. S. K. Prasad, D. S. Shankar Rao, S. Sridevi, J. Naciri and B. R. Ratna, J. Phys.: Condens. Matter, 2011, 23, 1.
22. (a) M. V. Gorkunov, M. A. Osipov, J. P. F. Lagerwall and F. Giesselmann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 51706; (b) M. V. Gorkunov, F. Giesselmann, J. P. F. Lagerwall, T. J. Sluckin and M. A. Osipov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 60701.
23. (a) K. Saunders, D. Hernandez, S. Pearson and J. Toner, Phys. Rev. Lett., 2007, 98, 197801; (b) K. Saunders, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 61708.
24. Y. Shen, L. Wang, R. Shao, T. Gong, C. Zhu, H. Yang, J. E. Maclennan, D. M. Walba and N. A. Clark, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 062504.
25. S. K. Prasad, D. S. Shankar Rao, S. Sridevi, C. V. Lobo, B. R. Ratna, J. Naciri and R. Shashidhar, Phys. Rev. Lett., 2009, 102, 147802.
26. R. Shashidhar, B. R. Ratna, G. G. Nair and S. K. Prasad, Phys. Rev. Lett., 1988, 61(5), 547.
27. L. Li, C. D. Jones, J. Magolan and R. P. Lemieux, J. Mater. Chem., 2007, 17, 2313.
28. J. C. Roberts, N. Kapernaum, F. Giesselman and R. P. Lemieux, J. Am. Chem. Soc., 2008, 130, 13842.
29. J. C. Roberts, N. Kapernaum, Q. Song, D. Nonnenmacher, K. Ayub, F. Giesselmann and R. P. Lemieux, J. Am. Chem. Soc., 2010, 132, 364.
30. Q. Song, D. Nonnenmacher, F. Giesselmann and R. P. Lemieux, J. Mater. Chem. C, 2013, 1, 343.
31. C. P. J. Schubert, C. Muller, M. D. Wand, F. Giesselmann and R. P. Lemieux, Chem. Commun., 2015, 51, 12601.
32. R. J. Birgeneau, C. W. Garland, A. R. Kortan, J. D. Litster, M. Meichle, B. M. Ocko, C. Rosenblatt, L. J. Yu and J. Goodby, Phys. Rev. A: At., Mol., Opt. Phys., 1983, 27, 1251.
33. L. D. Landau, Statistical Physics, Pergamon Press, Oxford, 3rd edn, 1980.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra10028g

‡ Authors have equal contribution.

---