Molecular dynamics simulation of Al–SiO2 sandwich nanostructure melting and low-temperature energetic reaction behavior
Jinping Zhanga,
Yubing Si*b,
Can Lengc and
Baocheng Yang*b
aCollege of Information Engineering, Huanghe Science and Technology College, Zhengzhou 450006, China
bHenan Provincial Key-Laboratory of Nano-composite and Applications, Institute of Nanostructured Functional Materials, Huanghe Science and Technology College, Zhengzhou, Henan 450006, China. E-mail: yubingsi@hhstu.infmm.cn; baochengyang@hhstu.infmm.cn
cNational Supercomputing Center, ChangSha, Hunan 410000, China
First published on 15th June 2016
Abstract
The heating and low temperature thermite reactions of the Al/SiO2 sandwich nanostructure are investigated by molecular dynamics simulations in combination with the reactive force field, ReaxFF. In this paper, the initial atomistic processes, thermal stability and energetic reaction properties of Al and SiO2 are presented. The results show that the melting temperature of the Al/SiO2 sandwich structure is ∼1400 K. The thermite reaction self-heating rates are determined by the thickness of the interfacial diffusion barrier at the interface in the nanoparticle.
1. Introduction
Superthermites,1 nanostructured energetic materials, have attracted much attention in the energetic community in recent years due to the properties of heat loss minimization via extremely fast propagating reaction rates, as well as the unique nanostructure that allows control over the reactivity by varying parameters such as particle size, morphology and local composition.2 Nanostructured energetic materials typically consist of a metal fuel (i.e., Al nanoparticles) and an oxide (CuO, Fe2O3, SiO2 and other oxide nanoparticles). Al/SiO2 thermite, for example, has generated great interest as an additive to thermite powders and its polycrystalline silicon is widely used in manufacturing solar cells, single crystals, and other high-tech applications.3 However, a substantial number of the traditional methods4 for polycrystalline silicon preparation have proven to be multistage, expensive and ecologically hazardous. Alternative ways for Si production are suggested by self-propagating high-temperature synthesis (SHS) technology5 and mechanochemical treatment,6 followed by considerable experimental studies using Auger electron spectroscopy (AES) and low-energy electron-loss spectroscopy (ELS) techniques. For example, a number of experimental studies5,6 on Al/SiO2 thermite have been carried out over the past several decades. This paper is motivated by the fact that no complete theoretical investigations have been performed on its energetic reaction properties. Therefore, the initial atomistic processes between Al and cristobalite SiO2 during the heating and thermite reaction at low initial temperature (300–500 K) are studied on the basis of the previous paper7 at high initial temperature (600–1100 K).Nowadays molecular dynamics (MD) atomistic simulation techniques play an essential role in providing physical insight understanding into atomic scale and thus can precisely predict the structure and the performances of various materials.8 Therefore, it is not surprisingly that MD studies have been conducted to predict the energetic properties of different nanostructured energetic materials.9 Currently, the traditional quantum mechanics (QM) models based on density functional theory (DFT) are computationally intensively used even for small clusters of 100 atoms or less. In the reactive force field, ReaxFF molecular dynamics (ReaxFF-MD) method9e can well model the bonds formation and broken several orders of magnitude faster than traditional DFT-QM models within the quantum chemical framework. In this paper, the reactive behavior between Al and SiO2 is simulated through using a molecular dynamics simulation in combination with the ReaxFF.10 To the best of our knowledge, the fundamental understanding of the molecular scale thermite reactions is not yet fully accomplished. Recently, an extremely computationally expensive11 ab initio study has been performed by a QM standpoint to examine the Al/Fe2O3 system, it is reported that 5 ps of simulation requiring over 985 h on 960 (3.2 GHz Intel Xeon) processors.6b Therefore, here we aim to obtain a fundamental understanding of the Al/SiO2 thermite reaction mechanisms through using classic molecular dynamics simulation with the ReaxFF. The investigations are focused on the initial atomistic processes during the heating and thermite reaction between Al and cristobalite SiO2.
2. Simulation model and method
All calculations are carried out by molecular dynamics (MD) simulations using the LAMMPS software package.12 The interatomic interactions are described by ReaxFF potential. ReaxFF13a is a reactive force field based on a general bond order/bond length relationship that provides smooth transitions from non-bonded to bonded systems and thus enables accurate description of the formation, transition, and complete dissociation of chemical bonds during reactive MD simulations in complex and large systems (>1 × 106 atoms). In the ReaxFF method, the forces are derived from a general energy expression| Esystem = Ebond + Eover + Eunder + Elp + Eval + EvdWaals + ECoulomb | (1) |
In this work we employed the recently developed Al/Si/O ReaxFF parameter set by B. Narayanan et al.10 This potential provides an accurate description of the structural and thermodynamic properties of several bulk phase oxides, silicates, and aluminates. These parameters have been shown to correctly predict relative order of stability of various polymorphs of eucryptite, and study atomic-scale mechanisms underlying solid-state phase transitions in eucryptite.10 Therefore, the present ReaxFF potential10 makes it suitable for the investigation of structure and properties of sub-oxides, atomic-scale mechanisms for phase transformations, as well as oxidation–reduction reactions. The Al/Si/O ReaxFF parameter for investigating the reaction properties of Al/SiO2 system is reliable and accurate.
The simulation model performed in the work is a stack of Al and SiO2 layers involving 1050(600 Al + 150 SiO2) atoms in an orthorhombic supercell with dimensions (Lx, Ly, Lz) = (28.6 Å, 24.8 Å, 30.2 Å) with periodic boundary conditions. The initial configuration of atoms is shown in Fig. 1. The cristobalite (SiO2) crystal is cut along the (111) planes and is placed in the supercell with the (111) direction parallel to the z direction. The (111) planes of cristobalite are attached to the (111) planes of the face-centered cubic Al crystal at the two interfaces. The simulation time step is set to 1.0 fs for all simulation cases. For the heating simulation, the temperature range in this study is from 300 to 2100 K (above the melting temperature). In order to achieve an equilibrium state, the system is kept at 300 K for 100 ps within a Nosé–Hoover thermostat scheme13f,13g of the NVT canonical ensemble. Then, a constant heating rate (0.6 K ps−1) is employed in the simulation; i.e., the particle is heated gradually by 3 × 106 time steps, which is equivalent to 3000 ps with temperature rising from 300 to 2100 K. The thermite reactional simulations in the nanoparticles model are carried out for three low initial temperatures (300 K, 400 K and 500 K) with the NVE microcanonical ensemble at adiabatic conditions in the nanoparticles model. In the NVE ensemble, the system is isolated from changes in moles (N), volume (V), and energy (E), which corresponds to an adiabatic process with no heat exchange. A microcanonical molecular dynamics trajectory may be seen as an exchange of potential and kinetic energy, with the total energy being conserved. The first step simulates the nanoparticles structure with the NVT ensemble using the Nosè–Hoover thermostat technique13f,13g at three different initial temperatures (300 K, 400 K and 500 K) for 50 ps. The second step simulates the structural changes and energetic properties of the system under the adiabatic conditions. The computing time is set to 600 ps for initial 300 K and 800 ps for initial 400 K and 500 K, then the NVE ensemble simulations are conducted. The computing time has been found to be sufficient, as trial simulations with longer durations yield minuscule changes of final temperatures in the computed initial temperatures.
3. Results and discussion
3.1 Heating simulation
For a constant heating rate of 0.6 K ps−1, we focus on Al/SiO2 sandwich's thermodynamic and structural properties. The typical particle evolution scenario shown in Fig. 2 display the side (yz) view of the entire system and are taken as radial representations for the whole system due to its constant volume property. From Fig. 2, it can be illustrated that the aluminum atoms diffuse inward the cristobalite with the increase of temperature, and the oxygen atoms within the cristobalite diffuse into the aluminum metal layers, forming part of Al–O bonds and gathering the silicon atoms together. At 1200 K, O atoms reach the outmost surface of the Al/SiO2 nanoparticles and continue to spread along with the temperature increasing. At 1600 K, large numbers of Si–O bonds break and become disconnected in the whole system and form abundant Al–O bonds at the same time. At 2000 K, pure silicon is found at the Al/SiO2 nanoparticles. A well-mixed liquid aluminum oxide forms and pure silicon leaves behind in the heating termination, which indicates a thermite reaction occurring during the heating process. The silica finally converse into silicon.Fig. 3 shows the potential energy profile of Al/SiO2 nanoparticles under 0.6 K ps−1 with the temperature ranging from 300 to 2100 K, which is very different from the pure aluminum particle as reported by Song et al.2e and our previous investigation.7 The potential energy of a pure Al particle has a linear increase followed by an abrupt jump. It can be seen that the potential energy of the Al/SiO2 exhibit a distinct V-shape with the increase of temperature; i.e., the nanoparticles experiences an early linear decline of potential energy at low temperatures, reaching a minimum value at ∼1400 K before a linear increase. Similar behavior is described in ref. 2e. The phenomenon is believed to be associated with the “hiccup” profile of temperature and pressure for Ni/Al nanolaminate as observed by Zhao et al.14 The V-shape of potential energy is result from a synergy between a disordering effect and the exothermic thermite reaction under continuous heating. The temperature of the whole system increases under heating conditions within a Nosé–Hoover thermostat scheme of the NVT canonical ensemble. External heat source can promote atomic mobility at relatively low temperatures. Consequently, an exothermic thermite reaction is induced by mutual diffusion of Al and O atoms in the fixed volume and the external heat source keeps solid structural disordering. The released energy will either go toward melting that makes atoms disorder or increasing atomic mobility that elevates the temperature. The V-shape of potential energy means the dominance of melting latent heat. The O–Al interaction which is confined in the fixed volume causes the initial potential energy decrease. Such a scenario is different from the potential energy increases for a pure element where the local order of atoms dominates atomic interaction. Clearly the minima in the potential energy are related to the melting phenomena so that the global melting temperature of the Al/SiO2 sandwich structure is ∼1400 K.
3.2 Thermite reactions of Al/SiO2 sandwich structure
Fig. 4 shows the time evolution of temperature at initial temperatures T0 = 300 K, 400 K and 500 K. From the Fig. 4, we can see that the Al/SiO2 at adiabatic conditions is accompanied by a significant self-heating after the relaxing of initial structures under the different initial temperatures, which reveals a large amount of heat generation after the thermite reaction occurring. Furthermore, an interesting characteristic of the thermite reaction is also shown in Fig. 4. Different initial temperatures bring about the different asymptotic temperature values (Tfin) (the average value of each simulation image at the last 0.2 ns). As shown in Fig. 4, the Tfin are 2602 K, 2326 K and 2034 K for the initial temperatures of 300, 400 K and 500 K, respectively, those are in good agreement with the reported adiabatic reaction temperature Tad of Al/SiO2 system by Fischer et al.,15 which is 2010 K without phase change and 1889 K with phase change. The MD Tfin results also reveal that Tfin decreases with increasing of the initial temperature. According to the simulation, the increasing temperature (Tfin − T0) is 2302 K, 1926 K and 1534 K, corresponding to the initial temperature of 300 K, 400 K and 500 K, respectively. | ||
| Fig. 4 Temporal evolution of temperature during the thermite reaction for Al/SiO2 with different initial temperatures. T (K) is the reaction temperature. | ||
The effective reaction time t at which the simulation temperature of the system reached T0 + 0.8(Tfin − T0) according to monitor the simulation temperature of the system, which is defined by Zhao et al.14
| T(t) = T0 + 0.8(Tfin − T0) | (2) |
The initial higher temperature slows down the reaction proceeding to completion, which is possibly the presence of an interfacial diffusion barrier at the Al–SiO2 interface according to the fact that it slows down the thermite reaction in the Al/SiO2 nanolaminates. What's more, the barrier may be quite weak in the initial temperature of 300 K, resulting in a very rapid reaction self-heating rate ∼10 K ps−1. However, it is even possible that there may be a stronger interfacial diffusion barrier exists in the initial temperature of 500 K since thermite reaction rate is more slowly (∼4 K ps−1) than before. These results are in good agreement with the theoretical investigation of in Al-coated Ni nanoparticle by Levchenko et al.16 about the research of the alloying reaction, as well as the experimental observation17 in which nanoparticles can dramatically decrease the ignition temperature of the reaction process.
3.3 Diffusion and its role in nanothermite reactions
To provide further insight into the simulation, we give the snapshots of the structure evolution for the initial temperature of 300 K and 500 K in Fig. 5 and 6, respectively. The time evolution snapshots of the side (yz) view of atomic configuration for both initial temperature (300 K and 500 K) display the whole thermite reaction process of Al/SiO2 sandwich structure. They are demonstrated that the oxygen atoms in cristobalite migrate into the aluminum metal to form aluminum oxide, leaving liquid silicon behind, which means that our simulation successfully reproduces the thermite reaction in the Al/SiO2 system consisting initially of thin aluminum and cristobalite layers. | ||
| Fig. 5 Snapshots of the side (yz) view of atomic configuration for the initial temperature of 300 K. | ||
 | ||
| Fig. 6 Snapshots of the side (yz) view of atomic configuration for the initial temperature of 500 K. | ||
When pre-heating of the Al/SiO2 sandwich model is up to 300 K and 500 K, a well-defined thin Al–O layer can be formed at the interface as shown in Fig. 5 and 6. But the barrier layer is quite weak for the initial temperature of 300 K and a stronger interfacial diffusion barrier grows with the model temperature up to 500 K. The Al–O layer prevents Si atoms diffusing into the Al side during the subsequent reacting at adiabatic conditions. As shown in the snapshots at 200 ps for the initial temperature of 300 K and 400 ps for the initial temperature of 500 K, the oxygen atoms diffuse toward the aluminum layer and reach the outmost surface to form part of Al–O bonds. Such phenomenon reveals two interesting characteristics of the thermite reaction. First, full conversion of silica into silicon completes, which is in good accordance with the experimental5c result conducts the hard-to-trigger silicon-producing SiO2–Al thermit-type SHS reaction in the electric arc ignited in an inert atmosphere under reduced pressure. Second, the higher initial temperature slows down the reactions proceed, which is also in excellent agreement with the result discussed above. The main reason is that the stronger interfacial diffusion barrier formed at the initial temperature of 500 K can slow down the thermite reaction in Al/SiO2 sandwich structure. This is in accord well with our previous investigation7 about the thermite reaction of Al/SiO2 at high initial temperature. But in that paper,7 we find that the thickness of interfacial diffusion barrier decreases with the increasing of the initial temperature when the initial temperature is higher than 600 K.
Ref. 2m sums up two different mechanisms to explain the observed behavior for nanoaluminum. The first mechanism states that the ignition and reaction of nanoaluminum has diffusion based mechanism where participating species diffuse across the oxide shell. The second is the melt dispersion mechanism, which requires the mechanical rupture of the shell and thereby release of the aluminum for ignition/reaction. Their studies showed that the highly violent reaction of Al/CuO is based on a diffusion mechanism. From snapshots of the structure evolution in Fig. 5 and 6, when reacting of Al/SiO2 at adiabatic conditions, the Al and O atom diffuse across the Al–O layer at the interface. So we have conclusions that the reactions are diffusion controlled. The diffusion capability of atoms during the reaction of Al/SiO2 can be further studied using the mean square displacements (MSD) by tracking individual atoms at the system. The MSD is based on atom random walk, and statistically an opposite diffusion trend is assumed for the system. We calculate the mean square displacements (MSD) by using the simulation data for 0–300 ps at the initial temperatures of 300 K and 500 K, which is shown in Fig. 7. The MSD is given as
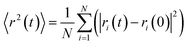 | (3) |
 | ||
| Fig. 7 Mean square displacements and fitted curve of all atoms in the thermite reaction, (a) initial temperature of 300 K; (b) initial temperature of 500 K. | ||
According to the MSD, we can get the self-diffusion coefficient with following Einstein relation:
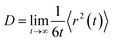 | (4) |
MSD is an important parameter for various components to understand the molecular dynamics of the multiphase system and can provide the system its self-diffusion coefficient. The self-diffusivity of the system is calculated from the Einstein relation. The resulting effective diffusion constant is 2.98 × 10−9 m2 s−1 and 1.33 × 10−9 m2 s−1 at 300 K and 500 K, respectively. This indicates that the bigger the effective diffusion constant, the faster the reactive speed of the thermite reactions. These further illustrate the fact that the overall chemical reaction is diffusion controlled.
3.4 Partial radial distribution function (RDF)
The partial radial distribution function (RDF) g(r) are also calculated for the better understanding of the atomic structures evolution and the reactive speed of the thermite reactions at different initial temperatures. Fig. 8 shows the g(r) of Al–Al, Si–Si, Al–O and Si–O pairs calculated at different time under the two different initial temperatures (300 K and 500 K) with the NVE ensemble. At t = 0 ps, the peak intensity and peak number of gAl–O(r) can be ignored compared to gSi–O(r). It reveals the domination statues of Si–O bond in the system. From Fig. 6, the peak intensity of gAl–Al(r) and gSi–O(r) weakens and the peak intensity of gAl–O(r) and gSi–Si(r) strengthens progressively as the reaction of aluminum and cristobalite proceeds, to be more details, the Al and SiO2 decreases steadily as the peak intensity of gAl–Al(r) and gSi–O(r) weakens, and the aluminum oxide and pure silicon phase increases as the peak intensity of gAl–O(r) and gSi–Si(r) strengthens. In Fig. 8, it is even more specifically that the second peak of gSi–Si(r) strengthening indicates the atom of Si becoming ordered in the whole system. The change of peak numbers gAl–Al(r), gSi–O(r), gAl–O(r) and gSi–Si(r) also indicates the decrease of reactants, solid Al and SiO2 phase, and the increase of the products, Si and aluminum oxide phase. The second peak of gSi–O(r) almost disappears especially at t = 400 ps for the initial temperature of 300 K and t = 600 ps for the initial temperature of 500 K, which indicates the Si–O bonds to be disconnected for the whole system. Corresponding to the end of the reaction, the peak intensities of gAl–O(r) and gSi–Si(r) reach to the maximum at t = 400 ps for the initial temperature of 300 K and t = 600 ps for the initial temperature of 500 K, on the contrary, the peak intensities of gAl–Al(r) and gSi–O(r) reach to the minimum and its curves becomes smooth, which indicates full conversion of silica into silicon complete. So we have conclusions that the reactive speed of the thermite reactions at the initial temperature of 300 K is faster than at the initial temperature 500 K.Compared to the first peaks of gAl–O(r) and gSi–O(r) at t = 200 ps for the initial temperatures of 300 K and 500 K are the higher peak of gAl–O(r) for the initial temperature of 300 K and the higher peak of gSi–O(r) for the initial temperature of 500 K, which also indicates that the reactive speed of the thermite reactions at the initial temperature of 300 K is faster than at the initial temperature of 500 K. It also can be implied the partial radial distribution functions g(r) of Al–Al, Si–Si, Al–O and Si–O pairs at last two sets pictures in Fig. 6, where the peak intensities of gAl–Al(r), gSi–O(r), gAl–O(r) and gSi–Si(r) are almost equal at different initial temperatures. But being aware that the computing times are 400 ps and 600 ps for the initial temperature of 300 K; however, it becomes 600 ps and 1000 ps when the initial temperature changes to 500 K.
4. Conclusions
The melting and low-temperature thermite reaction in Al/SiO2 system consisting initially of thin aluminum and cristobalite layers have been studied by molecular dynamics simulation and the ReaxFF. The melting temperature of the Al/SiO2 sandwich structure is ∼1400 K. Full conversion of silica into silicon has been found, which describes that a redox reaction to form aluminum oxide and simple substance silicon. We demonstrate that the thermite reactions will be very rapidly and the reaction self-heating rate is 10 K ps−1 if the reaction has been occurred before the formation of thin interfacial diffusion barrier layer at the interface. In this case, the initial temperature can be as low as 300 K. The thermite reaction occurs much more slowly when the reaction is ignited after the stage formatting of the interfacial diffusion barrier layer at the interface, and the reaction self-heating rate is 7 K ps−1 and 4 K ps−1 for the initial temperatures of 400 K and 500 K, respectively. The interfacial diffusion barrier slows down the thermite reaction in the nanoparticle.Acknowledgements
This work is supported by Zhengzhou Science and Technology Bureau (20150342) and the Science & Technology Development Program of Henan Province in China (Grant No. 142300410282).Notes and references
- S. F. Son, B. W. Asay, T. J. Foley, R. A. Yetter, M. H. Wu and G. A. Risha, J. Propul. Power, 2007, 23, 715 CrossRef CAS.
- (a) A. Prakash, A. V. McCormick and M. R. Zachariah, Nano Lett., 2005, 5, 1357 CrossRef CAS PubMed; (b) B. S. Bockmon, M. L. Pantoya, S. F. Son, B. W. Asay and J. T. Mang, J. Appl. Phys., 2005, 98, 064903 CrossRef; (c) S. M. Umbrajkar, S. Seshadri, M. Schoenitz, V. K. Hoffmann and E. L. Dreizin, J. Propul. Power, 2008, 24, 192 CrossRef CAS; (d) K. Sullivan, G. Young and M. R. Zachariah, Combust. Flame, 2009, 156, 302 CrossRef CAS; (e) P. X. Song and D. S. Wen, J. Phys. Chem. C, 2010, 114, 8688 CrossRef CAS; (f) J. L. Cheng, H. H. Hng, Y. W. Lee, S. W. Du and N. N. Thadhani, Combust. Flame, 2010, 157, 2241 CrossRef CAS; (g) K. Zhang, C. Rossi and G. A. A. Rodriguez, Appl. Phys. Lett., 2007, 91, 113117 CrossRef; (h) K. Zhang, C. Rossi, P. Alphonse, C. Tenailleau, S. Cayez and J.-Y. Chane-Ching, Appl. Phys. A, 2009, 94, 957 CrossRef CAS; (i) Y. Ohkura, S.-Y. Liu, P. M. Rao and X. Zheng, Proc. Combust. Inst., 2010, 33, 1909 CrossRef; (j) N. A. Manesh, S. Basu and R. Kumar, Combust. Flame, 2010, 157, 476 CrossRef CAS; (k) M. Petrantoni, C. Rossi, L. Salvagnac, V. Conédéra, A. Estève, C. Tenailleau, P. Alphonse and Y. J. Chabal, J. Appl. Phys., 2010, 108, 084323 CrossRef; (l) E. M. Hunt, S. Malcolm, M. L. Pantoya and F. Davis, Int. J. Impact Eng., 2009, 36, 842 CrossRef; (m) S. Chowdhury, K. Sullivan, N. Piekiel, L. Zhou and M. R. Zachariah, J. Phys. Chem. C, 2010, 114, 9191 CrossRef CAS; (n) K. T. Sullivan, W.-A. Chiou, R. Fiore and M. R. Zachariah, Appl. Phys. Lett., 2010, 97, 133104 CrossRef; (o) A. Ermoline, D. Stamatis and E. L. Dreizin, Thermochim. Acta, 2012, 527, 52 CrossRef CAS.
- D. Sarti and R. Einhaus, Sol. Energy Mater. Sol. Cells, 2002, 72, 27 CrossRef CAS.
- B. G. Gribov and K. V. Zinov'ev, Semiconductors, 2008, 42, 1475 CrossRef CAS.
- (a) Z. Yermekova, Z. Mansurov and A. S. Mukasyan, Int. J. Self-Propag. High-Temp. Synth., 2010, 19, 94 CrossRef CAS; (b) Z. A. Mansurov, R. G. Abdulkarimova, N. N. Mofa, N. K. Umarova and T. A. Shabanova, Int. J. Self-Propag. High-Temp. Synth., 2007, 16, 213 CrossRef CAS; (c) Y. M. Grishin, N. P. Kozlov, A. S. Skryabin, S. G. Vadchenko, N. V. Sachkova and A. E. Sytschev, Int. J. Self-Propag. High-Temp. Synth., 2011, 20, 181 CrossRef CAS.
- (a) T. A. Ketegenov and F. K. Urakaev, Int. J. Self-Propag. High-Temp. Synth., 2010, 19, 133 CrossRef CAS; (b) G. T. Hida and I. Liu, J. Am. Chem. Soc., 1988, 67, 1508 Search PubMed; (c) G. I. Ksandopulo, N. N. Mofa, T. A. Ketegenov, O. V. Chervyakova and O. A. Tyumentseva, Combust., Explos. Shock Waves, 2002, 38, 54 CrossRef.
- J. P. Zhang, Y. Y. Zhang, H. Li, J. X. Gao and X. L. Cheng, Acta Phys. Sin., 2014, 63, 086401 Search PubMed.
- (a) J. Hafner, Acta Mater., 2000, 48, 71 CrossRef CAS; (b) Y. B. Si, B. C. Yang, H. Qin, J. Y. Yuan, S. W. Wang, H. Y. Chen and Y. Zhao, J. Phys. Chem. C, 2015, 119, 8014 CrossRef CAS.
- (a) H. Z. Wu and S. J. Zhao, J. Phys. Chem. A, 2011, 115, 13605 CrossRef CAS PubMed; (b) N. H. Nguyen, A. Hu, J. Persic and J. Z. Wen, Chem. Phys. Lett., 2011, 503, 112 CrossRef CAS; (c) K. G. Vishnu, M. J. Cherukara, H. Kim and A. Strachan, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 184206 CrossRef; (d) E. V. Levchenko, A. V. Evteev, G. G. Löwisch, I. V. Belova and G. E. Murch, Intermetallics, 2012, 22, 193 CrossRef CAS; (e) A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 9396 CrossRef CAS.
- B. Narayanan, A. C. T. van Duin, B. B. Kappes, I. E. Reimanis and C. V. Ciobanu, Modell. Simul. Mater. Sci. Eng., 2012, 20, 015002 CrossRef.
- (a) F. Shimojo, A. Nakano, R. K. Kalia and P. Vashisha, Appl. Phys. Lett., 2009, 95, 043114 CrossRef; (b) F. Shimojo, A. Nakano, R. K. Kalia and P. Vashisha, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 066103 CrossRef PubMed.
- S. J. Plimpton, J. Comput. Phys., 1995, 117, 1 CrossRef CAS.
- (a) A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 9396 CrossRef CAS; (b) H. J. Qian, A. C. T. van Duin, K. Morokuma and S. Irle, J. Chem. Theory Comput., 2011, 7, 2040 CrossRef CAS PubMed; (c) J. Yeon and A. C. T. van Duin, J. Phys. Chem. C, 2016, 120, 305 CrossRef CAS; (d) A. Rahnamoun and A. C. T. van Duin, Phys. Chem. Chem. Phys., 2016, 18, 1587 RSC; (e) Z. H. He, X. B. Li, W. J. Zhu, L. M. Liu and G. F. Ji, RSC Adv., 2014, 4, 35048 RSC; (f) S. Nosè, Mol. Phys., 1984, 52, 255 CrossRef; (g) W. G. Hoover, Phys. Rev. A, 1985, 31, 1695 CrossRef.
- S. Zhao, T. C. Germann and A. Strachan, J. Chem. Phys., 2006, 125, 164707 CrossRef PubMed.
- S. H. Fischer and M. C. Grubelich, Theoretical Energy Release of Thermites, Intermetallics, Combustible Metals. in Proc. 24th Int., Pyrotechnics Seminar, Monterey, CA, 1998, pp. 1–6 Search PubMed.
- E. V. Levchenko, A. V. Evteev, D. P. Riley, I. V. Belova and G. E. Murch, Comput. Mater. Sci., 2010, 47, 712 CrossRef CAS.
- S. Dong, P. Hou, H. Cheng, H. Yang and G. Zou, J. Phys.: Condens. Matter, 2002, 14, 11023 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2016 |




