Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Forces and physical properties of the Langmuir monolayers of TiO2 particles at air/water interfaces after collisions by a particle in water†
Cathy E.
McNamee
*a and
Michael
Kappl
b
aDepartment of Chemistry and Materials, Faculty of Textile Science and Technology, Shinshu University, Tokida 3-15-1, Ueda, Nagano 386-8567, Japan. E-mail: mcnamee@shinshu-u.ac.jp; Tel: +81-268-21-5585
bMax Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany
First published on 31st May 2016
Abstract
The effect of a microsphere colliding with a particle stabilized emulsion was investigated by using a Langmuir monolayer of TiO2 particles at an air/pH 2 water interface and a TiO2 particle attached to a cantilever (probe) in the subphase. TiO2 particles with diameters (D) of 75 nm, 300 nm, 3 μm and 10 μm were used to determine the effect of the particle size on the physical properties of the interface. The Monolayer Particle Interaction Apparatus was used to measure the surface pressure–area/particle isotherms of the monolayers of the particles and the forces between the monolayers at different surface pressures and a 3 μm diameter TiO2 particle (probe) in the subphase, which acted as the colliding particle. The adhesion between the monolayer and the probe tended to decrease with a surface pressure increase. As the TiO2 particles are positively charged in pH 2 water, this result was explained by the increase in the proportion of the particle covered areas at the water surface, which would increase the charge density of the monolayer and therefore also the repulsive force. The stiffness of the monolayer tended to decrease as the surface pressure increased for the monolayers with the D ≤ 3 μm particles, rationalized by the decrease in the interfacial tension that accompanies a surface pressure increase. The stiffness, however, increased with a surface pressure increase for the D = 10 μm particles. This was explained by the strong capillary attractions that act between closely packed large particles at an air/water interface.
1. Introduction
Many cosmetics,1 food and drink products,2,3 pharmaceutical4,5 and technical products and applications6 require oils to be dispersed in water. A stable emulsion is needed so as to inhibit the coalescence of oil droplets and the coagulation of the phases in the materials, which would otherwise have detrimental effects on the properties of the product. Traditionally, surfactants are used for that purpose. However, environmental and health issues have driven the search for alternatives. One promising approach is the use of particles that adsorb at the oil/water interface, leading to so-called Pickering emulsions. The size, shape, chemical and mechanical properties, and packing density of the particles have been reported to determine the stability of Pickering emulsions.7,8 The types of oils and liquids used also affect the stabilizing ability of the particles.9In a real system, an emulsion droplet is not stationary in the water phase. It may collide with another droplet or dispersed particle while moving. Such collisions may change the arrangement of the particles at the interface and could consequently influence the mechanical stability and interaction of that droplet with other materials. The collision may also deform and bend the interface, causing buckling. The effect of a collision on the physical properties of an emulsion is not well understood.
The physical properties of a particle stabilized emulsion droplet are affected by the forces that act between the particles of the emulsion at the oil/water interface. For example, electrostatic forces cause repulsions between the particles, which are controlled by the particle surface charge. Common attractive force components include the hydrophobic, van der Waals, and lateral capillary interactions that act between neighboring particles.10 The strength of the repulsive and attractive inter-particle interactions within the emulsion are affected by the size, hydrophobicity, packing density of the particles at the interface, and the liquid type. The combination of these repulsive and attractive forces determines the physical properties of the emulsion droplet, such as its deformability and its interaction with other materials.
The effect of a particle colliding with a particle stabilized emulsion droplet is controlled by many factors, such as the impact strength, the relative sizes of the impacting particle and the particles at the oil/water interface of the emulsion, and the interactions between the impacting particle and the emulsion droplet. Additionally, the mechanical properties of the emulsion droplet will also affect the ability of the colliding particle to interact with the emulsion droplet. The elasticity and bending rigidity of colloidal monolayers at an air/water interface have shown that the monolayer may buckle or deform under stress.11,12 The collision of a particle would therefore also exert a point force on a monolayer of particles, and may cause changes in the physical properties of the monolayer. A droplet that can be easily deformed will be changed by the colliding particle to a larger extent than a more rigid droplet. As a result, the adhesive strength between the colliding particle and the emulsion droplet will be different for a soft droplet than a hard droplet.
A particle stabilized emulsion can be modelled by a monolayer of particles at an air/aqueous interface. The air corresponds to the hydrophobic oil phase, and the aqueous subphase corresponds to the water phase in which the oil is dispersed. The packing density of the particles in such a model system can be controlled by changing the surface pressure of the monolayer, where a low and high positive surface pressure represents a loose and a dense particle packing, respectively. The use of a model instead of a real particle stabilized emulsion enables the factors affecting the physical properties of the particle stabilized emulsion to be controlled more easily. This is because parameters such as the packing of the particles at the interface, the subphase type and the interaction of a foreign particle with the emulsion can be directly preset.
Stable Langmuir monolayers of bare TiO2 particles with diameters ranging from 300 nm to 10 μm have been made at an air/pH 2 water interface.13 We therefore used TiO2 particles of different sizes (diameter D = 75 nm, 300 nm, 3 μm and 10 μm) for the Langmuir monolayers. TiO2 is fairly hydrophilic with typical contact angles of 33 ± 4° for pH 2 water.13 The advantage of using such hydrophilic particles instead of hydrophobic particles, which are also known to form monolayers at air/aqueous interfaces, is that particle aggregation due to hydrophobic interactions can be avoided. The Monolayer Particle Interaction Apparatus (MPIA)14 was used to study the physical properties of the monolayers, while a colloid probe approached the monolayer from the bulk water phase. The MPIA is a combination of a Langmuir–Blodgett trough and a force measurement device. This instrument therefore enabled us to create the Langmuir monolayer of TiO2 particles at the air/pH 2 water interface and to control the packing density of the particles in the monolayer. The forces could be measured between the monolayer and a colliding particle (colloid probe), while the probe approached the monolayer from the bulk water phase. The stiffness of the monolayer could be obtained from the region of the force curves where the probe and the monolayer were in contact. The packing of the particles in the monolayer could be observed by using an optical microscope that was mounted above the Langmuir trough. The MPIA allowed us to control the collision parameters, i.e., approach speed and maximum contact force of the probe with the model emulsion. In this study, we used the same speed and maximum force in all the experiments and only varied the size of the particles in the monolayer and their packing densities. In this way, we could determine the effect of the particle sizes and their packing density in the monolayer on the physical properties of the monolayer at the air/pH 2 water interface upon the collision of an external particle (probe).
2. Experimental
2.1. Materials
The solvents used in this study were ethanol (EtOH, special high purity, Wako, Japan) and chloroform (CHCl3, special high purity, Wako, Japan). The water used in these experiments was distilled and de-ionised using a water purification system (Direct-Q3 UV, Millipore, USA) to give a conductance of 18.2 MΩ cm−1 and a total organic content of <5 ppm. The pH of all the aqueous solutions used in this study was adjusted to pH 2 by using hydrochloric acid (HCl, 30%, Wako, Japan). Throughout the Results and discussion section, the pH 2 water is referred to as “water”.Spherical TiO2 particles with a diameter of 75 nm (mixture of rutile and anatase, 10 wt% dispersion in water) were purchased from Aldrich, USA. Spherical silica particles coated with a TiO2 layer (sicastar, micromod Partikeltechnologie GmbH, Rostock, Germany) with D = 300 ± 60 nm, 3 ± 0.85 μm and 10 ± 2.5 μm were used for the larger TiO2 particles. The TiO2 in ethanol spreading solutions used to create the TiO2 particulate monolayers were prepared by firstly heating several mL of the aqueous particles solution in an oven for 2 h at 200 °C, in order to remove the aqueous solution in which the TiO2 particles were suspended. The particles were then allowed to cool overnight, dispersed in ethanol, and sonicated for 1 h.
The TiO2 colloid probe was prepared by attaching a D = 3 μm TiO2 particle to a cantilever (NP-S, Veeco Nano Probe™ Tips, nominal spring constant k = 0.12 N m−1) by using an XYZ micromanipulator and an epoxy resin glue (Araldite Rapid, Nichiban, Japan). The probes were cleaned prior to use by plasma treatment (2 min, medium power, PDC-32G-2 plasma cleaner, Harrick Plasma, Ithaka, NY).
2.2. Methods
The surface pressure of the monolayer was measured using a Wilhelmy plate of wet filter paper15 (S&S 595 Filter Paper Circles, Schleicher & Schuell GmbH, Dassel, Germany) suspended from a strain gauge (Riegler & Kirstein GmbH, Potsdam, Germany). The forces were measured between a colloid probe in the aqueous subphase and the film of particles at the air/aqueous interface, while the colloid probe was moved towards and away from the monolayer. Optical micrographs of the monolayers were obtained by attaching a digital camera (ueye SE, IDS GmbH, Obersulm, Germany) to the optical microscope (Axiotech Vario, Zeiss, Göttingen, Germany), which was mounted above the Langmuir trough.
The Π–A isotherms were converted to Π–area/particle isotherms by dividing A by the number of particles spread at the interface (Np), calculated using
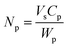 | (1) |
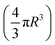 and the specific density of the particle, which was provided by the manufacture. R is the radius of the particle.
and the specific density of the particle, which was provided by the manufacture. R is the radius of the particle.
The magnitude of the adhesion force between the probe and the monolayer was obtained from the force curve minimum that was measured in the retraction force curves at a given surface pressure. The average adhesion force (Fad) was calculated by fitting a Gaussian curve to a histogram of the adhesive forces that were obtained from a minimum of 50 force curves. The reduced Fad data were calculated by dividing Fad by R2, where R is the radius of the probe; this allowed Fad of different deformable systems to be compared.14 The effective stiffness (SN)14 of the monolayer at the air/aqueous interface was calculated by dividing the slope of the linear contact region of the force curves measured between the probe and the monolayer at the air/pH 2 water interface (S1) by the slope of the linear contact region of the force curves measured between the same probe and the hard mica substrate in water (S2).
3. Results and discussion
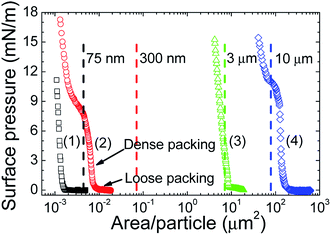
The monolayers made from the D = 75 nm, 300 nm, 3 μm or 10 μm TiO2 particles at the air/pH 2 water interface gave surface pressure–area/particle isotherms with zero or near zero surface pressure at large area/particles (Fig. 1). The surface pressure increased as the area/particle was decreased, confirming that all the TiO2 particle sizes formed monolayers at the air/pH 2 water interfaces. Surface pressure–area/particle regions attributable to monolayers of particles with loose and dense packing16 could be recognized in the isotherms. The loose packing regime was apparent by the larger area/particle values and the non-linear surface pressure–area/particle relationship before the onset of the steep slope for surface pressures up to between 1 and 3 mN m−1. The densely packed region commenced at higher surface pressures after the loose packing regime. The D = 300 nm and 10 μm particles also showed a plateau at high surface pressures and at area/particle values smaller than those observed for the dense packing regime.The origin of the plateau observed in the 300 nm and 10 μm monolayers and the stability of the particles at the air/water interface for all the monolayers was investigated by comparing the area of one particle (Ap), calculated using R2 (see dashed lines in Fig. 1), to the area/particle where the dense packing regime was observed. The 75 and 300 nm particles showed an Ap which was much larger than the area/particle observed in the densely packed regime. This result indicates that some of the particles spread at the air/water interface were instable at the air/water interface and sank into the subphase. The plateau observed for the 300 nm particles is therefore explained by the movement of some of the particles from the interface to the subphase bulk. The fact that the 75 nm particles did not show a plateau suggests that the 75 nm particles were less stable at the air/water interface than the 300 nm particles. The area/particle seen in the dense packing regime for the D = 3 and 10 μm particles corresponded reasonably well with Ap, where the experimental values were the same or slightly larger than Ap. The particles with D ≥ 3 μm were concluded to be stable at the air/water interface and therefore were thought not to sink into the subphase. The reason why the area/particle values seen in the dense packing regime were larger than Ap is explained by the deviation in the particle sizes and the error in the estimation of the number of particles spread at the air/water interface. As the 10 μm particles were stable at the air/water interface, the plateau seen for the monolayer of 10 μm particles is not due to the movement of the particles into the subphase bulk. Instead the plateau is explained by wrinkling, caused by attractions between the particles in the monolayer. The fact that the 3 μm particles did not show this plateau suggests that the inter-particle interactions between the 3 μm particles were weaker than those between the 10 μm particles.
As all the particle sizes used here showed loose and dense packing regimes, we were able to determine the effect of the particle size and particle packing on the forces between a colliding particle (probe) and a monolayer of particles.
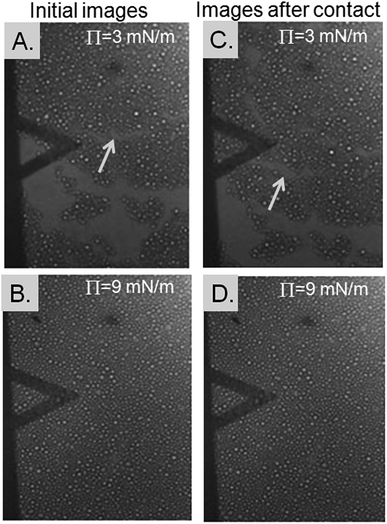
The TiO2 particle monolayer at the water surface was imaged with a camera by using the monolayer made of the 10 μm particles, while the forces were measured between the probe and the monolayer. The images show the monolayer at a lower surface pressure of 3 mN m−1 and a higher surface pressure of 9 mN m−1 before and after a force measurement, i.e., before and after contact by the probe (Fig. 2). A surface pressure of 3 mN m−1 gave areas corresponding to a bare water surface and areas that were covered with the particles (Fig. 2A and C). This result indicated that 3 mN m−1 gave a loose packing regime. Islands of TiO2 particles could also be observed, which moved after the probe contacted the monolayer (compare Fig. 2A and C). A surface pressure of 9 mN m−1 resulted in a water surface that was completely covered by particles, i.e., no areas of bare water surface were observed (Fig. 2B and D), indicating a dense packing regime. No marked differences were observed before and after the probe contacted the monolayer.
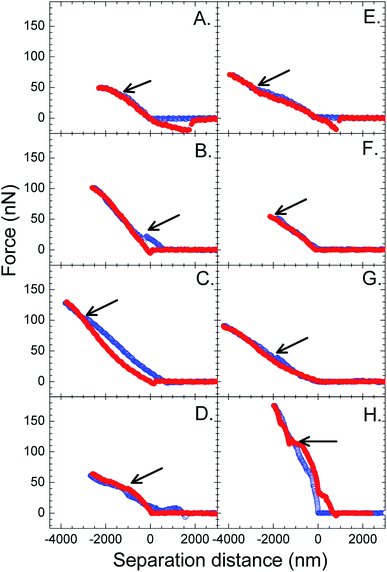
Examples of force curves measured between the monolayers of TiO2 particles at the water surface and a 3 μm TiO2 probe at a low (Π = 3 mN m−1) and a high (Π = 9 mN m−1) surface pressure are shown in Fig. 3. The approach force curves showed a repulsive force at smaller distances. The linear repulsive region indicates the region where the probe and the monolayer were in contact. The slope of this region allowed us to calculate the stiffness of the monolayer. It is thought that this region may be related to the bending rigidity of the monolayer. A stiffness of less than one (slope < 1) indicates that the monolayer is being deformed by a point force (probe). A discontinuity (break-through) could be seen in the repulsive force region of the approach force curve, as indicated by the arrows. The discontinuity suggests that the probe could break and enter the monolayer of particles.
The retract force curves in Fig. 3 showed a contact region followed by an adhesion, before the probe and the monolayer separated completely. The separation event was identified from a jump from an attractive force back to a zero force. The adhesion was divided by the square of the probe radius to give Fad/R2,14 so that adhesion values of different experiments reported in the literature can be compared in the future.
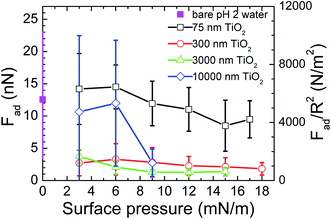
The average adhesion forces that were determined from the force curves measured between a bare air/water interface and a 3 μm TiO2 probe or between TiO2 particulate monolayers at air/water interfaces at various surface pressures and a 3 μm TiO2 probe are plotted in Fig. 4. Both the adhesion forces (Fad) and reduced adhesion forces (Fad/R2) are shown as a function of the surface pressure of the monolayers. The adhesion of the bare air/water interface was either comparable or higher than the values measured for the air/water interface with the monolayers of the TiO2 particles. This high adhesion of the bare water surface can be explained by a capillary attraction, attractive van der Waals forces, and hydrogen bonding between the probe and the water surface. The magnitude of the adhesive force and the size of their error bars also tended to decrease as the surface pressure of the monolayer increased.
A bare air/water interface gave the highest adhesion with a reasonably high error. The error in those data is explained by the variation in the force curves measured at the air/water interface and by fact that different TiO2 particles were used as the probes for different monolayer systems. A monolayer of particles gave adhesions whose magnitude and associated error depended on its surface pressure. High surface pressures gave the lowest adhesions and smaller error bars. Low surface pressures gave higher adhesions with higher error bars. The magnitude of the error bars associated with the adhesion forces of the monolayers shows the variation in the force curves measured for each monolayer at each surface pressure. Fig. 2 showed that the air/water interface was not completely covered by the particles at low surface pressures. Thus, force curves would sometimes be measured at bare air/water interfaces, which would give high adhesions, or sometimes at air/water interfaces that were partially or completely covered by particles, which would give lower adhesions. The averaging of these adhesions would give adhesion values with an apparent high error.
The interaction between a probe and a particle covered interface has been measured from the air side by other groups.17 Adhesions were measured between the probe and a particle free air/water interface. The magnitude of these adhesions decreased when particles were added to the interface. As the probe was being brought from the air to the air/water interface, the adhesions were explained by a capillary interaction acting between the probe and the interface. The presence of the particles was thought to reduce the adhesion, due to a reduction in the perturbation of the interface shape. Although we measured the forces between the probe and the monolayer from the water side, we also observed a decrease in the magnitude of the adhesions between the probe and the monolayer when the packing density of the particles increased. Thus, the presence of particles at an air/water interface is thought to reduce the adhesion of the interface to a probe, when the force between the probe and the interface is measured from either the air or the water side. This result indicates that the presence of the particles at the interface changes the forces acting at the interface, suggesting that the presence of the particles influences the deformability of the interface.
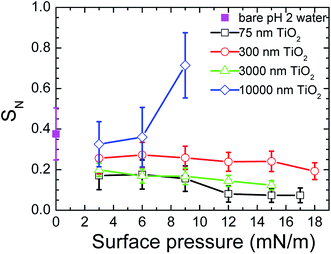
Fig. 5 shows the effect of the surface pressure on the effective stiffness (SN) of the bare air/water interface or a monolayer of particles. The SN values were determined from the force curves measured between a bare air/water interface and a probe in the water or between a monolayer of particles at the air/water interface and a probe in the water. The effective stiffness of the monolayer was calculated using the slope of the repulsion in the approach force curve before the break-through. The SN of the bare air/water interface was greater than the SN of the monolayers containing particles with D ≤ 3000 nm for all surface pressures. The SN of the monolayers with the 10 μm particles was greater than the SN of the bare air/water interface at high surface pressures. The variation in SN with the surface pressure of the monolayer depended on the size of the particles used in the monolayer. Type (1) showed a tendency for SN to decrease with a surface pressure increase. This was seen was for monolayers with particles of D = 75 nm, 300 nm and 3 μm. Type (2) showed a SN increase with a surface pressure increase. This was observed for monolayers with particles of D = 10 μm. The error bars for the SN values measured for the monolayer of particles at the air/water interface is a consequence of the variation in force curves that were measured for the same monolayer at the same surface pressure. These different force curves are thought to come about from the movement of the particles due to a low packing density or from the particle movement caused by the impact of the probe.
The strength of the adhesive force is considered to be controlled by (1) the interactions between the probe and the water surface and (2) the deformability of the interface. A deformable interface with particles smaller than the probe can deform and wrap around the probe to give a large probe–monolayer contact surface area, whereas a non-deformable (stiff) interface or one with particles larger than the probe cannot deform and wrap around the probe, thus resulting in only a small contact area. The adhesive energy between the probe and a surface will increase with an increased contact area. Thus, a monolayer that is deformable and/or shows an attraction to the probe would give a high adhesion.
Increasing the surface pressure of a monolayer at an air/water interface causes the surface tension to decrease. The deformability of an interface has been reported to increase with a surface tension decrease.18 In the case of a monolayer of particles at an air/water interface, such a coarse-grained picture is expected to comply if one averages over many interfacial particles. This interpretation is therefore thought to hold, if the probe contacts and presses the monolayer with a force that is spread over a greater area, i.e., if the probe is bigger than the particles forming the monolayer. As a result, the adhesion between the probe and the monolayer should increase with a surface pressure increase for monolayers with a particle diameter ≤3 μm. The stiffness of the monolayers of the TiO2 particles at the air/water interface tended to decrease with a surface tension decrease (surface pressure increase). However, the adhesion was seen to decrease with a surface pressure increase. In the case of a monolayer composed of 10 μm particles, pressing a monolayer of 10 μm spheres with a 3 μm sphere corresponds to a point force on one of the 10 μm spheres. The big sphere is held by the water interface with a high surface tension and this interface must balance the force. Therefore, the surface tension is expected not to decrease with a surface pressure increase, if a 3 μm probe is pressed against a monolayer composed of D = 10 μm particles. As the surface tension effect cannot explain the adhesion decrease for all the TiO2 particle sizes used in this study, causes other than a surface tension change must contribute to the change in the adhesion with a surface pressure increase for monolayers of particles with D ≤ 10 μm.
Increasing the surface pressure also causes the area of the water surface covered by the particles to increase. A TiO2 particle that is immersed in water adjusted to pH 2 is positively charged.19 Thus, the repulsion between the TiO2 probe in the water and the monolayer of TiO2 particles at the air/water interface is expected to increase due to the increased charge density of the monolayer. This would cause the adhesion to decrease. Regardless of the particle size used in the monolayers, we observed a tendency for the adhesion to decrease with an increased surface pressure of the monolayer. The decrease in adhesion with a surface pressure increase is therefore explained by the increased charge density of the air/water interface.
The way the stiffness of the monolayer changed with the surface pressure was seen in Fig. 5 to be affected by the size of the particles used in the monolayer. It is therefore necessary to understand how the particle size affects the stiffness. The effect of the particle size on the stiffness can best be understood by comparing the data of the monolayers at dense packing. This is because the contributions from the bare water surface are small in this region. The images in Fig. 2 showed that the water surface was completely covered by TiO2 particles at Π = 9 mN m−1. Thus, we can use the SN data of Fig. 5 and compare the values of the different monolayer particle sizes that were measured at Π = 9 mN m−1. This comparison had the added advantage that the surface tension effect could be neglected, because the data from the same surface pressure were being compared. A larger SN was seen for the TiO2 particles with D = 10 μm than the values obtained for the TiO2 particles with D < 10 μm.
The size of the particles in the monolayer will influence how easily the particles in the monolayer can be moved and displaced by the impacting probe, and therefore how much the monolayer will be disrupted and how much its stiffness will decrease as a result. Monolayers with particles that are smaller than the probe are expected to show more particle movement or displacement than the monolayers with particles that are larger than the probe, due to the difference in size between the particles and the probe. The particles moved by the probe are expected to roll and slide on top of each other. A greater movement or displacement of the particles in a monolayer will cause the monolayer to be disrupted more, resulting in its stiffness appearing lower. Fig. 5 showed that the stiffest monolayer was achieved when the size of the particles used in monolayer (D = 10 μm) was larger than the size of the colloid probe that collided with the monolayer (D = 3 μm). Thus, the size of the particles making up the monolayer and their size relative to the probe are thought to affect the stiffness.
The stiffness of the monolayer will also be affected by the forces acting between the particles in the monolayer. The DLVO interactions that can act between two TiO2 particles in contact with an aqueous solution are the electrostatic force and the van der Waals force. The repulsive electrostatic force dominates at larger particle separations, while the van der Waals force dominates at smaller particle separations. Monolayers with a loose packing density should ideally show particles that are discrete and separated, i.e., no aggregates or islands, due to the electrostatic repulsions. Monolayers with a dense packing density should show particles that are packed closely, due to the attractive van der Waals forces. Fig. 2, however, showed islands of particles at a low surface pressure that corresponded to a loose packing density regime rather than individually isolated particles. This result indicates that forces other than the DLVO forces were also present in the system.
A non-DLVO force that causes attractions between particles at an air/water interface is the capillary force. The weight induced lateral capillary force acts between particles at an air/aqueous interface, as a result of the deformation of the interface due to the effect of gravity.10 Its presence can result in an attraction between the particles at an air/water interface.20,21 The effect of the size of the particles on the weight induced lateral capillary force can be estimated by calculating the weight induced lateral capillary force between two similar spherical TiO2 particles, when the size of the particles is varied. The lateral capillary interaction energy for particles separated by small distances (L ≪ κ1), was calculated from22
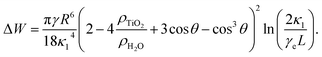 | (2) |
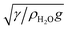 , where g and γ were the standard gravity (9.81 m s−2) and the surface tension of water (0.07 N m−1).
, where g and γ were the standard gravity (9.81 m s−2) and the surface tension of water (0.07 N m−1).
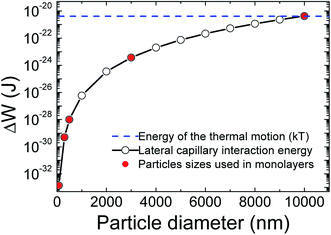
Fig. 6 shows the effect of particle size on the lateral capillary interaction energy (ΔW), calculated using eqn (2). The solid circles in the figure correspond to the sizes of the particles used to make the TiO2 particulate monolayers in this study. The lateral capillary interaction was seen to increase with a particle size increase, where ΔW for the D = 300 nm, 500 nm, 3 μm and 10 μm particles was 3.6 × 103, 7.2 × 104, 2.7 × 109 and 3.0 × 1012 times larger than that obtained for the 75 nm particles. The magnitude of the energy of the thermal motion (kT, where k and T are the Boltzmann's constant and temperature, respectively) at T = 298 K was included in Fig. 6 (blue dashed line), in order to compare the magnitude of the energy of the thermal motion to the calculated weight induced lateral capillary force. The strength of the capillary interaction can be seen to reach kT for the 10 μm spheres, indicating that aggregation due to capillary forces is possible. This result corresponds with the aggregation of the 10 μm particles at low surface pressures that was seen in Fig. 2a and with the associated effects reported elsewhere.20,21 The strong lateral capillary interactions that acted between the 10 μm TiO2 particles in the monolayer help explain the large SN observed at higher surface pressures in Fig. 5.
The stiffness of the monolayer is therefore thought to be affected by (1) the lateral adhesions between the particles in the monolayer at the water surface and (2) the relative size difference between the particles in the monolayer and the probe.
The lateral adhesions between the particles in the monolayer at the water surface are considered to include the van der Waals attraction and the capillary attractions, the latter of which become strong if the particles in the monolayers are large enough. These attractions would lead to a monolayer whose structure would be less changed or damaged by the probe, causing it to appear stiffer. The strength of these lateral attractions increases as the separation distance between the particles decrease and the particles come into contact. Although entirely discrete particles were not observed at any surface pressure, a surface pressure increase would decrease the separation between the islands of particles at the interface. Thus, the areas in the monolayer which are connected by the van der Waals and capillary forces would increase with a surface pressure increase. As a result, the ability of parts of the monolayer to resist deformation and breakage by the probe would increase.
The stiffness of the monolayer is also affected by the relative size difference between the particles in the monolayer and the probe. Particles at the surface can be displaced more if the probe is larger, causing the monolayer stiffness to appear weaker. The larger stiffness seen for the 10 μm particles is also explained by the fact that the displacement of the 10 μm particles at the surface by the 3 μm probe was less than the displacement of the particles in a monolayer with particle sizes smaller or the same size as the probe. The capillary adhesions between the D = 10 μm particles help explain why the particles were displaced less by the probe, when the size of the particles in the monolayer was D = 10 μm and not D ≤ 3 μm.
Monolayers with particle sizes (D = 10 μm) greater than the probe (D = 3 μm) were seen to give a stiffer monolayer at close packing (high surface pressures) than monolayers with particle sizes (D = 75 nm, 300 nm, 3 μm) smaller than the probe at close packing. The larger stiffness can be explained by the decreased ability of the probe to move the particles in the monolayer as the size of the particles in the monolayer was increased. In the case of the monolayers with particle sizes (D = 75 and 300 nm) smaller than the probe (D = 3 μm), the probe was in contact with more than one particle and therefore interacted with and moved a network of particles. The fact that the 300 nm particles gave a stiffer monolayer than the 75 nm particles can be explained by the increased inter-particle van der Waals and capillary interaction attractive forces that accompany a particle size increase. In the case of the monolayers with particle sizes (D = 3 μm) the same as the probe size (D = 3 μm), the probe may interact with one particle at the interface or at the boundary area between several particles. We explain the lower stiffness of the monolayer with the D = 3 μm particles compared to the D = 300 nm particles due to the contact of the probe at the junctions between the particles at the air/water interface. Increasing the number of particles in the probe–monolayer contact area appears to decrease the movement of the particles in the monolayer by the probe, when inter-particle attractions exist. This difference may be related to a change in the elasticity of the monolayers with a decrease in the size of the particles in the monolayer.
The adhesion between the monolayer and the probe is affected by the ratio of the particle covered water surface as to the bare water surface. Increasing the surface pressure increases the ratio of the particle covered water surface as to the bare water surface, which would decrease the adhesion between the monolayer and the probe. This repulsion, however, does not appear to be large enough to inhibit the probe from displacing or moving the particles in the monolayer, resulting in a decreased stiffness.
A monolayer of particles can therefore be made to appear stiffer and therefore change less after the collision of a probe by using (1) particles of the same charge as the probe, i.e., utilizing the electrostatic force, (2) particles large enough to give a strong capillary force between the particles, i.e., increasing the adhesion between the particles in the monolayer, and (3) particles that are larger than the probe, i.e., particles that are harder to be moved by the probe. The capillary force effect appears to be the most effective in increasing the stiffness of the monolayer.
Comparison of the stiffness of monolayers made from our particles (particle sizes between 75 nm and 10 μm) and monolayers made from surfactants (octadecanol or stearic acid at an air/water interface)23 shows that the stiffness is comparable, when the size of the particles in the monolayer were ≤3 μm. This result was surprising, as the particles were much larger than the size of a surfactant molecule. The small size of the surfactants means that the lateral capillary attractions between surfactant molecules are negligible. The attractive interactions between the surfactant molecules that affect the stiffness are therefore thought to be the van der Waals and hydrophobic interactions. The particles used to make the monolayer were hydrophilic. The attractive interactions between the particles at the air/water interface are therefore thought to be the van der Waals and lateral capillary interactions, where the magnitude of the inter-particle lateral capillary interactions depends on the size of the particles. The stiffness of the particle monolayers appears to became larger than the surfactant monolayers, when large particles are used (D = 10 μm). Thus, hydrophilic particles are thought to be able to make monolayers that are stiffer than amphiphilic surfactants when the particles are big enough to display large attractive inter-particle lateral capillary interactions.
In order to understand how a collision affects the stiffness of an emulsion droplet using the results from our study of monolayers of particles at air/water interfaces, we must consider the difference in the shapes of the particle adsorbed interfaces. An air/water interface is flat. However, an emulsion droplet is curved. Curvature has been reported to decrease surface tension.24 Thus, an emulsion droplet with particles large enough to display inter-particle capillary attractions and with particles that are compressed to a high packing density is expected to have a lower interfacial tension than a monolayer of the same particle type at an air/aqueous interface, which is compressed to the same packing density. This would result in the physical properties of the emulsion droplet corresponding to those of a monolayer of particles at an air/water interface with a lower surface pressure. Such a system would show a lower stiffness. Thus, a collision of a particle with an emulsion droplet is anticipated to cause the emulsion droplet to deform more than a monolayer of particles at an air/aqueous interface compressed to the same packing density, causing the stiffness of the droplet to be reduced more than that observed in a monolayer of particles at an air/water interface.
4. Conclusions
The adhesion between a monolayer of particles at an air/water interface and a probe tended to decrease with a surface pressure increase. This is explained by the increase in the area of the particle covered water, which gives rise to an increased charge density and therefore an increased electrostatic repulsion. A surface pressure increase also showed the tendency for the stiffness of the monolayer to decrease for the monolayers with the 75 nm to 3 μm sized particles. This was explained by the decrease in the surface tension of the interface. The D = 10 μm particles gave a monolayers whose stiffness increased with a surface pressure increase. This was explained by the presence of the strong capillary attractions that act between large particles in contact at an air/water interface. It is therefore concluded that the strength of a monolayer of particles, i.e., the stiffness of the monolayer, and its ability to interact with a colliding particle, i.e., adhesion ability, can be modified by changing the sizes of the particles used in the monolayer and the density to which they are compressed, i.e., surface pressure.Acknowledgements
The authors would like to thank Prof. Hans-Juergen Butt (Max Planck Institute for Polymer Research, Mainz, Germany) for valuable discussions. This study was partially performed through the Hosokawa Powder Technology Foundation (Japan) and the JSPS KAKENHI Scientific Research C (General) research grant entitled “Determination and control of the forces at deformable interfaces and the effect of particle adsorption”.References
- W. G. Cho, Journal of the Society of Cosmetic Scientists of Korea, 2010, 36, 1–16 Search PubMed.
- D. Rosusseau, Curr. Opin. Colloid Interface Sci., 2013, 18, 283–291 CrossRef.
- E. Dickinson, J. Sci. Food Agric., 2013, 93, 710–721 CrossRef CAS PubMed.
- S. Lam, K. P. Velikov and O. D. Velev, Curr. Opin. Colloid Interface Sci., 2014, 19, 490–500 CrossRef CAS.
- M. Wahlgren, J. Engblom, M. Sjoo and M. Rayner, Curr. Pharm. Biotechnol., 2013, 14, 1222–1234 CAS.
- V. Alvarado, X. Wang and M. Moradi, Energies, 2011, 7, 1058–1086 CrossRef.
- W. Huang, L. Qiang and Z. Yan, Prog. Chem., 2007, 19, 214–219 Search PubMed.
- R. Aveyard, B. P. Binks and J. H. Clint, Adv. Colloid Interface Sci., 2003, 100, 503–546 CrossRef.
- Y. Chevalier and M.-A. Bolzinger, Colloids Surf., A, 2013, 439, 23–34 CrossRef CAS.
- P. A. Kralchevsky and K. Nagayama, Adv. Colloid Interface Sci., 2000, 85, 145–192 CrossRef CAS PubMed.
- P. J. Yunker, M. Gratale, M. A. Lohr, T. Still, T. C. Lubensky and A. G. Yodh, PRL, 2012, 108, 228303 CrossRef PubMed.
- D. Vella, P. Aussillous and I. Mahadevan, EPL, 2004, 68, 212 CrossRef CAS.
- C. E. McNamee, S. Yamamoto, H.-J. Butt and K. Higashitani, Langmuir, 2011, 27, 887–894 CrossRef CAS PubMed.
- C. E. McNamee, M. Kappl, H.-J. Butt, K. Higashitani and K. Graf, Langmuir, 2010, 26, 4574–14581 Search PubMed.
- G. T. Barnes and I. R. Gentle, Interfacial Science an Introduction, Oxford University Press, Oxford, 2005, p. 86 Search PubMed.
- F. Bremse and M. Oettel, J. Phys.: Condens. Matter, 2007, 19, 413101 CrossRef.
- W. He, N. Şenbil and A. D. Dinsmore, Soft Matter, 2015, 11, 5087 RSC.
- D. Y. C. Chan, R. R. Dagastine and L. R. White, J. Colloid Interface Sci., 2001, 236, 141–154 CrossRef CAS PubMed.
- W. Wang and Y. Ku, J. Membr. Sci., 2006, 282, 342–350 CrossRef CAS.
- J. Bleibel, A. Domínguez and M. Oettel, Eur. Phys. J.: Spec. Top., 2013, 222, 3071–3087 CrossRef.
- J. Bleibel, A. Domínguez, M. Oettel and S. Dietrich, Soft Matter, 2014, 10, 4091–4109 RSC.
- M. G. Nikolaides, A. R. Bausch, M. F. Hsu, A. D. Dinsmore, M. P. Brenner, C. Gay and D. A. Weitz, Nature, 2002, 420, 299–301 CrossRef CAS PubMed.
- C. E. McNamee, M. Kappl, H.-J. Butt, H. Nguyen, S. Sato, K. Graf and T. Healy, J. Phys. Chem. B, 2012, 116, 13731–13738 CrossRef CAS PubMed.
- E. Santiso and A. Firoozabadi, AIChE J., 2006, 52, 311–322 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra09499f |
| This journal is © The Royal Society of Chemistry 2016 |