A thermodynamic approach of self- and hetero-diffusion in GaAs: connecting point defect parameters with bulk properties
Abstract
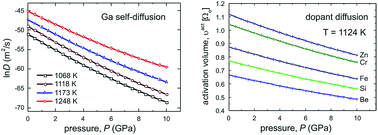
The self- and hetero-diffusion in GaAs is investigated in terms of the cBΩ thermodynamic model, which connects point defect parameters with the bulk elastic and expansion properties. Point defect thermodynamic properties, such as activation enthalpy, activation volume, activation Gibbs free energy, activation entropy and isobaric specific heat of activation, are calculated as a function of temperature for Ga, H and various n- and p-type dopants (Si, Be, Cr, Fe and Zn) diffused in GaAs. The present calculations are in good agreement with the reported experimental results. The pressure dependence of Ga self-diffusion is also investigated and the diffusivities and activation volumes are predicted at different temperatures from ambient pressure up to 10 GPa, above which GaAs is transformed into the orthorhombic structure. The activation volumes of dopants are also estimated at high temperature (1124 K), as a function of pressure.

 Please wait while we load your content...
Please wait while we load your content...