Morphology and thermal properties of novel clay-based poly(ethylene 2,5-furandicarboxylate) (PEF) nanocomposites

Abstract

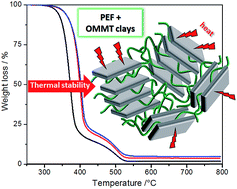
Novel nanocomposites of bio-based poly(ethylene 2,5-furandicarboxylate) (PEF) and organo-modified montmorillonite (OMMT) clays were prepared. Sample morphology was investigated by means of transmission electron microscopy (TEM) and X-ray diffraction (XRD) that revealed a good dispersion of the clay layers in the PEF matrix. Moreover, the effect of clays on the nanocomposites' thermal behavior was determined by differential scanning calorimetry (DSC) and thermogravimetric analysis (TGA). The results show that the presence of clays induces a slight nucleating effect on the PEF crystallization. More remarkably, the clay layers increase significantly the thermal stability of PEF by postponing the initial degradation (+20 °C).