A quantum chemical approach towards understanding stability and tautomerism of 2-imino-2H-pyran derivatives

Abstract

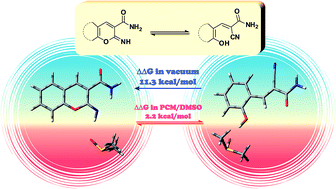
The ring-chain tautomerism of 2-imino-2H-pyran derivatives annelated with an aromatic or aliphatic ring and their transformation into corresponding 2-pyridons were theoretically studied based on the relative stabilities of two series of model isomers calculated by the DFT B3LYP/aug-cc-pVDZ method. This approach, augmented by the analysis of specific interactions between the solute and solvent molecules (DMSO or acetone) in 1 : 1 complexes and simulation of the bulk solvent medium by PCM, allowed a good agreement with the experimental data for 2-imino-2H-coumarines and explained their ring-chain tautomerism in different media. The main reason governing the stabilization of the open-chain isomers was found to be the specific intermolecular interaction of the hydroxyl groups of these isomers with a solvent molecule.

---

Introduction

The molecular structure of heterocycles is a fundamental subject of organic chemistry that fully determines the compound's properties and applications. In this regard, 2-imino-2H-pyran derivatives represent a well-known class of heterocycles, but their extensive practical use is accompanied by an insufficiently clear understanding of the factors that define their stability. Thus, 2-imino-2H-1-benzopyrans, also known as 2-iminocoumarins, 2-imino-2H-chromenes or 2H-chromen-2-imines are unique heterocycles. They can be readily synthesized in diverse structural variations and possess the exocyclic imino group, which is capable of further transformations. A great number of reactions with nucleophiles^1–14 and electrophiles^12–16 using these compounds as starting materials, as well as rearrangements of the 2-iminopyran ring^3,7–11 are common in synthesis of heterocyclic systems that contain the coumarin moiety^{3–8,12–14} and other heterocycles.^13,17–29 Importantly, 2-iminocoumarin derivatives are known to possess a spectrum of biological activity,^30–37 they are used as ligands for metal complexes,^37–40 as luminescence compounds,^24,40–50 and as models for studying hydrogen bonds.⁵¹ 2-Iminocoumarins 4 are generally synthesized by the Knoevenagel reaction starting from salicylic aldehydes 1 and active methylene compounds 2 followed by intramolecular cyclization of the hydroxyl and cyano groups, as depicted in Scheme 1.

Scheme 1 Reaction conditions: (a) EtOH or i-PrOH, piperidine (catal.), rt or Δ; (b) i-PrOH, piperidine (catal.), rt; (c) i-PrOH, MW 100 °C/5 min.

In contrast, the isolation and characterization of 2-imino-2H-pyran derivatives without annulated aromatic or heteroaromatic ring are exceptional.⁵² The intermediate formation of such derivatives was, however, postulated to rationalize heterocyclization reactions^53–55 of dienolate salts 6.^55–58 The acid-catalyzed hydrolysis of 2-iminocoumarins 4 proceeds under very mild reaction conditions to give corresponding coumarin derivatives.^{4–8,12–14} An analogous reaction for dienolate salts 6 resulting in formation of corresponding 2-pyrons under similar reaction conditions has been recently described.⁵⁹ Interestingly, reactions of 2-iminocoumarins 4 as well as dienolate salts 6 with N-nucleophiles readily proceed in acetic acid, but lead to different types of products, namely, N₂-substituted 2-iminocoumarins^1,2,6–14 and N₁-substituted 2-pyridone derivatives.^56,57 Moreover, the significant difference in the reactivity of 2-iminocoumarins 4 and dienolate salts 6 is represented by a possibility of the salts to be further transformed into 2-pyridones 8, presumably via addition of dimethylamine to the intermediate iminopyrane 7 at nodal C–O–carbon followed by the pyran ring opening and ring closure (ANRORC mechanism).^53,54 In contrast, a similar transformation of 2-iminocoumarin derivatives (4 → 9) is obviously restricted due to the necessity of nucleophilic substitution of the phenolic OH-group, and such reactions have not been described in the literature with the exception of one artifact published without substantial evidence and discussion.¹³

Regardless of the importance of 2-imino-2H-pyran derivatives the questions of their stability and ring-chain tautomerism have not been studied sufficiently well. This especially concerns 2-mino-2H-pyrans 7, the intermediate formation of which has been only suggested, but not observed experimentally.

More data about the structure and stability of 2-iminocoumarins is available. A hundred years ago, Perkin and Robinson had pioneered in formulation of 2-iminocoumarin structure 10 (Scheme 2) for a product of demethylation of ethyl 2-cyano-3-(2,3-dimethoxyphenyl)acrylate.⁶¹ The structure was drawn on the basis of the chemical properties of the compound, namely, the ready hydrolysis of its imino group yielding the corresponding ethyl coumarin-3-carboxylate. In a much later work, O'Callaghan et al. synthesized the same compound by the Knoevenagel approach and its open-chain structure 11 in the crystalline phase was proven by a single-crystals X-ray study.⁶² Interestingly, another representative of such compounds (12) can exist in a cyclic 2-iminocoumarin form in the crystalline phase as it was also proven by single-crystals X-ray diffraction study.¹⁵

Scheme 2 Isomerization of 2-iminocoumarin derivatives: structures 11 and 12 are confirmed by X-ray single crystal analysis. Degree of the isomerization (DI) is given for solutions of compounds 13 in DMSO-d₆ at 293 K. The designations “s-trans-“ and “s-cys-“ are used as in original article.⁶⁰

The O'Callaghan's group has studied the isomerization of 2-iminocoumarin-3-carboxamides in detail by NMR and IR spectroscopy (Scheme 2).⁶⁰ These compounds exist in the cyclic form 13 in solid state as well as in deuterochloroform (CDCl₃) and acetone-d₆ solutions. However, in dimethyl sulfoxide-d₆ (DMSO-d₆) solutions, an equilibrium between cyclic tautomer 13 and acyclic rotamers s-trans- and s-cys-14 exists, though the latter is present in a quite low extent (ca. 5%). The degree of the isomerization clearly depends on the position and nature of the substituent R in the aromatic ring. The isomerization of compounds 16 (ref. 60) and 17 (ref. 63) in DMSO-d₆ was not detected.

It can be assumed that the stability of 2-iminopyran ring depends on both the molecular structure and the nature of the medium. There is enough experimental evidence that these compounds can exist in cyclic 4 and acyclic 3 forms. For their aliphatic analogues, on the contrary, the acyclic form was isolated and characterized only as its salt 6, and the formation of cyclic imino form 7 was postulated to mechanistically rationalize the transformations of salts 6.

In this work we aim to clarify the reasons governing the ring-chain tautomerism of 2-imino-2H-pyran derivatives including the influence of the annelated ring in different media using quantum chemical calculations.

Calculation details

The quantum chemical calculations were carried out at the DFT B3LYP/aug-cc-pVDZ level of theory with Gaussian'03 program package.⁶⁴ This density functional of GGA type reproduces geometry parameters well enough and requires no frequency scaling⁶⁵ in thermodynamic computations. The basis set should contain diffuse functions as long as we need to describe intermolecular interactions; it also compensates for the well-known hydrogen bond strength overestimation inherent to the “magic” B3LYP/6-31G** method.

We found the global minima on the molecular potential energy surfaces (PESs) through the following procedure meant to be an exhaustive conformational search. The geometry of the structures Ar1-3 and Alk1-3 together with all their possible staggered rotamers were pre-optimized with the semiempirical AM1 method. Then all resulting conformers were re-optimized at the B3LYP/aug-cc-pVDZ level of theory (see ESI, Tables S1–S3,† for details). After this, a few most stable conformers were selected. Usually, 4–5 of the conformers falling within 2–3 kcal mol⁻¹ difference range from the global minimum were subjected to further calculations.

At the next stage, the influence of the solution medium on the molecular structure and properties was studied. Initially it was done in the framework of the Polarizable Continuum Model (PCM⁶⁶), using DMSO and acetone as actual solvents from the experiment. This model is denoted below as “PCM/solvent”. Then the specific interactions were partly taken into account. A solvent (DMSO or acetone) molecule was allowed to form hydrogen bond(s) with the solute molecule. The model of 1 : 1 solute–solvent complex is denoted below as “+solvent”.

Finally, the most accurate treatment of solvent effects in this work was the application of a mixed physico-chemical model, in which the 1 : 1 solute–solvent complex is enveloped by PCM solvent. This model is denoted below as “+solvent, PCM/solvent”.

All the structures discussed below represent minima on the potential energy surface, which was confirmed by frequency computations. The thermodynamical properties were evaluated at 298 K with no frequency scaling. The relative energy as well as process energy referred to below is the difference in the Gibbs free energy of two structures.

The basis set superposition error (BSSE), present in the 1 : 1 complexes, was neglected for the following reasons. Firstly, the diffuse basis set shells reduce the error value. Secondly, it will be cancelled to a great deal when comparing different 1 : 1 complexes, in particular, when ranging the complexes for the stability.

Visualization of the computed structures was done using the GaussView program.⁶⁷

Results and discussion

Two series of isomers Ar1-3 and Alk1-3 have been chosen to be the model structures (Scheme 3) as the simplest representatives of molecules 3, 4, 9 and 6 (in its conjugate acid form), 7, 8 (Scheme 1). Since the isomerization of 2-iminocoumarin-3-carboxamides (13) is most well-studied⁶⁰ (Scheme 2) we have chosen the derivatives possessing the amide group (EWG = CONH₂) in order to compare calculation results with the available experimental data. An additional type of tautomerism can be expected for molecule Alk1 (Scheme 4), and the CH tautomers (Alk1a and Alk1b) can take different conformations. Owing to the absence of the aromatic fragment, the enolate 6 can be transformed into 2-pyridone derivatives 8 via intermediate formation of 7 under relatively vigorous reaction conditions (Scheme 1). This indicates the higher stability of 8 compared to 6 (in its conjugate acid form) and 7, apparently, this must be reflected in the calculation results. The highest stability of the 2-pyridone derivatives, Ar3, in the aromatic series is also expected by structural analogy. That's why we also used 1H-quinolin-2-one Ar3 and aliphatic carbocycle Alk3, as a checkpoint for verification of our calculation results.

Scheme 3 Model structures chosen for quantum chemical calculations. Possible rotamers taken into account are marked with the curved arrows. Only the chair conformation of cyclohexane moiety of Alk1-3 was taken into account.

Scheme 4 The expected tautomerism for model molecule Alk1. Possible rotamers taken into account are marked with the curved arrows. Only the chair conformation of cyclohexane moiety of Alk1 was taken into account.

The initial calculations revealed that in vacuum the intramolecular hydrogen bond between the amide hydrogen and the imino group (as illustrated in Fig. 1, Alk2_1) is more favorable than any other intramolecular interaction (Alk2_4 and Alk2_2). It can be attributed partially to better planarity of the molecule supporting the conjugation. This trend was observed in all further calculations for both the aliphatic (Alk2) and aromatic (Ar2) imines (see ESI, Table S22†). For the aliphatic series, the OH-tautomers (Alk1_1 and Alk1_9) were found to be significantly more stable than C–H tautomers (Alk1a_3 and Alkb_1). This trend is also common for all computed structures (ESI, Tables S17, S18, S25–S27†).

Fig. 1 Structures and relative stability (in vacuum) of the most stable Alk2 rotamers with different intramolecular hydrogen bonding and the most stable tautomers of Alk1 of different types.

Calculated relative stability of Ar1-3 and Alk1-3 shows clearly that in vacuum (Table 1, vacuum) the energy of the isomers is simultaneously decreased from open-chain structures (Ar1, Alk1) through imino forms (Ar2, Alk2) to the most stable 2-pyridone derivatives (Ar3, Alk3). The Gibbs free energy of the imine → open form isomerisation for the aromatic series (Table 2, vacuum) corresponds to the equilibrium constants of order 10⁻⁹, while for the aliphatic series—10⁻⁵. Therefore the equilibrium is shifted completely to the more stable imino form.

Table 1 Structure and relative stability of the most stable isomers in series Ar1-3 and Alk1-3 (ΔG₂₉₈, kcal mol⁻¹). The media influence is modelled by PCM and/or the formation of 1 : 1 complexes with a solvent molecule by an intermolecular hydrogen bond with a mobile proton as indicated in brackets. The molecular geometry is shown as it was obtained in PCM, in the cases where the most stable isomers were different in vacuum and PCM, both structures are shown

Code	Optimized structure^a
	Vacuum	PCM/DMSO	+DMSO	+DMSO, PCM/DMSO	+Acetone	+Acetone, PCM/acetone
a The optimized structure was chosen between all possible conformers/tautomers as the global energy minimum (see ESI for the full list of structures).
Ar1
	36.1	34.8	34.4	31.6	34.7	33.2
Ar2
	24.9	28.1	28.2	28.6	27.0	28.3
Ar3
	0
Alk1
	32.5	37.5	35.4	33.7	33.6	35.6
Alk2
	26.7	30.8	31.4	32.4	29.9	32.0
Alk3
	0

---

Table 2 Isomerization energies (ΔG₂₉₈, kcal mol⁻¹) of imino (2) to open-chain (1) forms in aromatic and aliphatic series (see Scheme 3)

Process	Vacuum	PCM/DMSO	+DMSO	+DMSO, PCM/DMSO	+Acetone	+Acetone, PCM/acetone
Ar2 → Ar1	11.3	6.7	6.2	3.0	7.7	4.9
Alk2 → Alk1	5.8	6.7	2.2	1.3	3.7	3.6

---

Importantly, the structures of the most stable open-chain isomers are not similar for the aromatic and aliphatic sequences. In contrast to Ar1 isomers, where the global energy minimum corresponds to the structure Ar1_6, the most stable in vacuum open-chain isomer of the aliphatic series (Alk1) is Alk1_9 that contains resonance-assisted⁶⁸ intramolecular hydrogen bond (OH⋯O) between its hydroxyl and amide groups (Table 1). The bond is mainly responsible for 5.5 kcal mol⁻¹ decrease in the imine → open form isomerization energies between the aromatic and aliphatic sequences (Table 2, vacuum). It is worth noting that omitting the most stable structure Alk1_9 results in almost the same isomerisation energy for the both series, 11.3 kcal mol⁻¹ for Ar1_6/Ar2_1 and 11.0 kcal mol⁻¹ for Alk1_1/Alk2_1 (ESI, Table S25†). The aromatic analogue of Alk1_9, that is Ar1_9, lies 1.2 kcal mol⁻¹ above the global minimum Ar1_6 for the open form structure (ESI, Table S22†). In this case, the resonance stabilization of the hydrogen bond would break the aromatic conjugation.

However, as illustrated in Scheme 2, for 2-iminocoumarin-3-carboxamides dissolved in DMSO-d₆, the equilibrium between imino and open forms is observed. This experimental fact cannot be rationalized from the calculation results discussed above. The obvious cause of this is our neglecting the role of the solvent. As the first attempt to take into account the solvent influence, the Polarizable Continuum Model (PCM) was further applied. The use of DMSO medium within PCM affected notably the calculation results (Table 1; PCM/DMSO). In the aromatic series, the isomerization energy decreases considerably, but in the aliphatic one it increases slightly resulting in the same value of 6.7 kcal mol⁻¹ for the both series (Table 2). The different influence of PCM is obviously related to different types of the most stable open-chain conformer structures in the aromatic and aliphatic series, cf. Ar1_6 and Alk1_9. The calculated isomerization energy value corresponds to the equilibrium constant of order 10⁻⁵, that still disagrees with the observed equilibrium between isomers 13 and 14, 15.

In general, the relative stability of Ar1/Ar2 and Alk1/Alk2 calculated in vacuum and PCM/DMSO shows that the imino forms are more stable, this agrees with the experimental data concerning amides 13 found to exist in imino form in CDCl₃, and also predicts that imino form Alk2 will exist in media of similar nature. As expected (Scheme 1), the calculation results agree with the thermodynamic possibility for the reactions Alk1 → Alk2 → Alk3 and Ar1 → Ar2 → Ar3 to be carried irreversibly at least in the solvents of low solvating ability under conditions allowing the molecules to overcome the activation barriers.

From our results we assumed that specific solvation effects are responsible for the equalization of thermodynamic potentials of these two isomers, and we have to involve structure of the solvent molecules into the calculations. Structures of 1 : 1 complexes of model compounds with DMSO molecule were further built. Since DMSO is a basic aprotic solvent, its molecules tend to form intermolecular hydrogen bonds with acidic protons due to S=O oxygen atom. It is known that hydrogen atoms of the methyl groups form only weak hydrogen bonds.^69,70 So the strongest solute–DMSO interaction should be a hydrogen bond of O–H (N–H) protons to the DMSO oxygen atom. The bonds with DMSO molecule are stronger with OH group⁷¹ as the most acidic center among all the other functions containing mobile protons in Ar1/Ar2 and Alk1/Alk2. Formation of such bonds in DMSO could provide the observed stabilization of the open-chain forms Ar1 and Alk1 in this solvent. Therefore, two types of 1 : 1 complex were considered that contain the following proton donating groups H-bonded with DMSO molecule. The first one is with active in the cyclization OH group for the open forms (Ar1, Alk1) and NH group for imino derivatives (Ar2, Alk2). The second one is with the amide group (Fig. 2). It should be noted that in rotamers Ar1_9 and Alk1_9 OH-group is involved in an intramolecular hydrogen bond. Here the solvent molecule can attach to the amide group only.

Fig. 2 Selected structures and relative energies of 1 : 1 complexes formed by attachment of one DMSO molecule to hydroxyl, imino, and amide groups of the acyclic (Ar1, Alk1) and cyclic (Ar2, Alk2) forms (+DMSO, PCM/DMSO model). In all cases the most stable conformer of each type was chosen preliminary basing on the PCM/DMSO model results.

The results obtained for 1 : 1 complexes of the model molecules with DMSO in vacuum are represented in Table 1 (+DMSO). The structures Ar3 and Alk3 hold as the most stable ones. Also for the both series the open-chain structures appeared to be the least stable. However, these calculations provide considerable energetic leveling of cyclic and acyclic tautomers for the aliphatic series, estimating the isomerization energy for Alk1_9 (CONH₂–CN) → Alk2_1 (CONH₂) to be 2.2 kcal mol⁻¹. At the same time, for the aromatic series, the solvation model has no such a significant effect, cf. Ar1_6 (OH) → Ar2_1 (CONH₂) (Table 2).

Finally, the relative stability was studied within +DMSO, PCM/DMSO model. The DMSO complexes of 2-pyridone derivatives Ar3 and Alk3 were the most stable isomers (Table 1, +DMSO, PCM/DMSO) as expected. Comparison of calculated stability of different complexes participating in the ring-chain tautomerism is shown in Fig. 2. For the cyclic forms (Ar2 and Alk2) the 1 : 1 complexes formed by imino and amide groups are nearly isoenergetic (Fig. 2). The most stable solvates of the open-chain isomers are formed by OH-group, Ar1_6 (OH) and Alk1_2 (OH). For both imino forms, the most stable 1 : 1 complex is formed by amide groups, Ar2_1 (CONH₂) and Alk2_1 (CONH₂). However, the stability of the complexes formed by imino groups, Ar2_1 (NH) and Alk2_1 (NH), differs insignificantly, below 1 kcal mol⁻¹ in the both series (Fig. 2). The open form, in contrary, gives the most stable 1 : 1 complex with OH group, while complex with amide group is less stable by 3.3 kcal mol⁻¹ and even less for the aliphatic compound (6.2 kcal mol⁻¹). Note, a significant proton transfer in Alk1_2 (OH) is observed showing formation of a strong intermolecular hydrogen bond (Fig. 2).

Calculations of the 1 : 1 complexes in PCM/DMSO show considerable stability convergence of the open-chain and cyclic imino forms (Table 1, +DMSO, PCM/DMSO). The value of 1.3 kcal mol⁻¹ providing the equilibrium constant of order 0.1 is close to reproduce the experimental data on the tautomeric equilibrium displayed in Scheme 1. Interestingly, in contrast to the +DMSO model results, the solvate of rotamer, Alk1_9 (CONH₂), with intramolecular hydrogen bond appeared to be less stable than acyclic solvate formed by the hydroxyl group, Alk1_2 (OH). It is related probably to destabilization of the intramolecular hydrogen bond in DMSO.⁵¹ This fact underlines the deficiency of our +DMSO model and necessity of the PCM envelope (see ESI, Tables S23 and S24,† for details).

Thus it can be concluded that the main factor of the open form stabilization (Ar1, Alk1) in the DMSO medium is the strong hydrogen bond between the OH-group and the oxygen atom of DMSO. Our application of a phisyco-chemical solvation model that takes into account only one molecule of the solvent already provides considerable leveling of the tautomeres energies. The estimated equilibrium constant value approaches the experimentally determined one for 2-iminocoumarins.

Comparison with another solvent: acetone

Hydrogen bond formation can be also expected in the acetone medium. But as it was mentioned above, the cyclic form of 2-iminocoumarin-3-carboxamides is experimentally observed in their acetone solutions. In contrast to DMSO, the calculation results for acetone (+acetone, PCM/acetone) show that the equilibrium between open-chain and cyclic imino forms is shifted completely to the more stable imino form. The Gibbs free energy of the imine → open form isomerisation for the aromatic sequence (4.9 kcal mol⁻¹) corresponds to the equilibrium constants of order 10⁻⁴, while that for the aliphatic sequence (3.6 kcal mol⁻¹) to 10⁻³ (Table 2, +acetone, PCM/acetone).

The acetone molecule is expected to form weaker intermolecular hydrogen bonds compared to the DMSO. Formation of intermolecular hydrogen bonds with acetone stabilizes also the open-chain structures Ar1 and Alk1, though less efficiently (Table 1, +acetone, PCM/acetone; see ESI† for the other data from our +acetone and +acetone, PCM/acetone models).

Analysis of the specific interactions

The crucial role of the specific intermolecular interactions in DMSO guided us towards deeper analysis of this aspect. There are several empirical relations established between electron density properties and atom–atom interaction energy.^72–75 The most relevant here is the well-known formula of Espinosa et al.⁷² relating energy density in a special point on the hydrogen bond line to the bond energy. The formula describes the medium-strength hydrogen bonds well, but also has been applied sometimes to the bonds (or rather, interaction lines) between other atoms, failing mostly in the complicated cases like metalorganic bonds.

As seen from Table 3 (for full data see ESI, Tables S32 and S33†), DMSO molecule forms the strongest intermolecular hydrogen bond with the enol OH group of Alk1_2 (OH), −24.4 kcal mol⁻¹. The similar hydrogen bond in the aromatic derivative Ar1_6 (OH) is weaker, −16.1 kcal mol⁻¹, but also very strong compared to all other intermolecular specific interactions. In Alk2_1 (NH) and Ar2_1 (NH) the hydrogen bond energy between the imino group hydrogen atoms and DMSO molecules corresponds to −5.0 and −4.6 kcal mol⁻¹, and energy of the hydrogen bonds formed by the amide group hydrogen atoms and oxygen atoms of DMSO is varied from −5.9 to −7.9 kcal mol⁻¹ depending on structure. The strongest intramolecular interaction is found in Alk1_9 (CONH₂), this is the resonance-assisted hydrogen bond formed by the enol hydrogen and the amide oxygen (−41.5 kcal mol⁻¹; such high estimation underlines inapplicability of the Espinosa's formula to the strongest hydrogen bonds). But Gibbs energy of this isomer calculated in PCM/DMSO is 4.0 kcal mol⁻¹ higher than the most stable open-form solvate Alk1_2 (OH) (Fig. 2). The similar hydrogen bond in Ar1_9 (CONH₂) is much weaker (−25.4 kcal mol⁻¹) because its resonance assistance is accompanied with disruption of the aromatic ring. That makes the aromatic analog, Ar1_9 (CONH₂), to be less stable, as compared to Ar1_6 (OH), by 7.3 kcal mol⁻¹ (Fig. 2), and the formation of Ar1_9-type structures is hardly expectable in any medium. While the resonance-assisted hydrogen bond is very strong, it is not strong enough to compensate the sum of two factors: unfavorable geometry of seven-membered pseudo-cycle and some entropy loss due to the additional ring formation. On the other hand, the break of intramolecular hydrogen bond N–H⋯N=C of imino forms (the bond energy varies from −6.9 to −7.4 kcal mol⁻¹ for the both series) in DMSO and the ring opening itself is compensated by formation of the strong intermolecular hydrogen bond of OH-functions with DMSO molecule medium, −24.4 kcal mol⁻¹ for Alk1_2 (OH) and −16.1 kcal mol⁻¹ for Ar1_6 (OH). The open-chain molecules are additionally stabilized by non-classical intramolecular hydrogen bonds C–H⋯OH (−4.1 kcal mol⁻¹ for Ar1_6 (OH) and −4.0 kcal mol⁻¹ for Ar1_6 (CONH₂), see ESI for more detailed Tables S32 and S33†) and interactions between aromatic C–H and CN-group, −2.3 kcal mol⁻¹ for both above mentioned 1 : 1 complexes. Such interactions are absent in aliphatic analogs Alk1_2 (OH) and Alk1_2 (CONH₂). Instead, there is an interaction between partially negatively charged oxygen atom of the hydroxyl and partially positively charged carbon atom of the cyano group (HO⋯CN, energy estimation is −2.7 and −2.4 kcal mol⁻¹, correspondingly). These interactions probably determine the structure of the most stable rotamers.

Table 3 Hydrogen bond length and estimated strongest specific interaction energy values⁷² in Ar1-2 and Alk1-2 1 : 1 complexes in the +DMSO, PCM/DMSO model

Structure	Interaction	l, Å	E, kcal mol^−1	Structure	Interaction	l, Å	E, kcal mol^−1
	All intermolecular		−17.5		All intermolecular		−25.3
	O–H⋯O=S	1.606	−16.1		O–H⋯O=S	1.505	−4.4
	All intramolecular		−6.4		All intramolecular		−2.7
	All intermolecular		−7.5		All intermolecular		−7.5
	N–H⋯O=S	1.859	−6.8		N–H⋯O=S	1.864	−6.7
	All intramolecular		−6.3		All intramolecular		−2.4
	All intermolecular		−9.0		All intermolecular		−9.1
	N–H⋯O=S	1.814	−7.8		N–H⋯O=S	1.808	−7.9
	All intramolecular		−25.4		All intramolecular		−47.1
	C=O⋯HO	1.505	−25.4		C=O⋯HO	1.386	−41.5
	All intermolecular		−4.6		All intermolecular		−5.0
	N–H⋯O=S	2.040	−4.6		N–H⋯O=S	1.994	−5.0
	All intramolecular		−7.4		All intramolecular		−6.9
	N–H⋯N=C	1.903	−7.4		N–H⋯N=C	1.929	−6.9
	All intermolecular		−6.5		All intermolecular		−6.6
	N–H⋯O=S	1.911	−5.9		N–H⋯O=S	1.910	−5.9
	All intramolecular		−7.0		All intramolecular		−6.5
	N–H⋯N=C	1.923	−7.0		N–H⋯N=C	1.950	−6.5

---

Thus, as confirmed by the calculation of the specific interaction energies, the substantial strength of intermolecular hydrogen bonds between hydroxyl groups and DMSO molecules is the main stabilizing factor towards formation of ring-open isomers from the 2-iminopyrans. In the real solutions, the solvation occurs simultaneously by all solvation centers, and the solvation of amide group with one DMSO molecule contributes into stabilization of all CONH₂-solvates with very close intermolecular interaction energy values (the energy is varied from −6.5 to −7.5 kcal mol⁻¹ for the both series). Therefore, the 1 : 1 complexes formed by amide group can be neglected in comparison of relative stability. Taking this into account allows further leveling the relative stability of the open-chain and cyclic imino forms, providing the isomerization energies of Ar1_6 (OH) and Ar2_1 (NH) to be 2.2 kcal mol⁻¹ and for Alk1_2 (OH) and Alk2_1 (NH) to be 0.8 kcal mol⁻¹. Thus, both consideration of the calculation results, with taking into account the solvation of amide groups and with neglecting this solvation, provide considerable leveling of the Gibbs energies of two tautomers for the both series showing that the quantum chemical calculations of 1 : 1 complexes of the solute molecules with DMSO in PCM/DMSO is the adequate enough model of the studied tautomerism.

Finally, the estimated energies of similar specific interactions with acetone generally have lower values, especially for the strongest intermolecular hydrogen bonds, formed by phenol and enole groups with the interaction energy of −11.0 and −14.5 kcal mol⁻¹, correspondingly, for Ar1_6 (OH) and Alk1_2 (OH). The strength of intermolecuar hydrogen bonds formed by imino groups and acetone, N–H⋯O=C, also decreased as compared to that with DMSO, −3.7 and −4.0 kcal mol⁻¹ for Ar2_1 (NH) and Alk2_1 (NH), correspondingly (for all data see ESI, Tables S32 and S33†). The interaction energy with amide groups is ranged from −3.8 to −5.1 kcal mol⁻¹, depending on the solute structure. These results are in line with the recent investigation using NMR clearly demonstrating that the phenolic OH-group forms stronger hydrogen bonds with DMSO-d₆ than to acetone-d₆.⁷⁶

Thus, the energy of itrermolecular hydrogen bond formation between OH-groups and acetone is insufficient to stabilize the open forms Ar1 and Alk1 in this medium. The equilibrium is predicted to be completely shifted to the imino form, as it is observed for 2-iminocoumarins experimentally.⁶⁰

Conclusions

For aromatic and aliphatic tautomeric series of 2-imino-2H-pyrans the trends in relative stability are generally the same. In two series of isomers Ar1-3 and Alk1-3 the most stable structures are 2-pyridone derivatives, Ar3 and Alk3, independent of the medium nature. The cyclic imino forms, Ar2 and Alk2, appear to be significantly more stable than the open forms, Ar1 and Alk1, in vacuum, in polar solvents without specific interactions (as modeled by PCM/DMSO), and in solvents with weak specific interactions (such as acetone). The specific solute–solvent interactions (especially involving classic hydrogen bonds) in the aliphatic sequence are stronger, and the energetic levelling of the open-chain and cyclic imino forms is sharper. Moreover, in contrast to the aromatic sequence, the conformer containing a resonance-assisted intramolecular hydrogen bond, Alk1_9, has a relatively high stability and is found to be the most stable open form in a calculation not involving the use of PCM.

In DMSO medium a significant energetic leveling is observed for the corresponding 1 : 1 complexes of the imino and open forms with one DMSO molecule in PCM. The main factor responsible for this and influencing the ring-chain tautomerism is the energy of specific interactions between solvent molecules and proton-donating groups of the open and cyclic forms. The strongest intermolecular hydrogen bonds are formed between DMSO molecules and the hydroxyl groups of the open forms, and these hydrogen bonds stabilize the open forms in DMSO. On the contrary, the acetone solvation energy is insufficient to stabilize the open-chain form. That is why the tautomerism is not observed in this medium. Thus, taking into account just a single solvent molecule (in our +solvent, PCM/solvent model) already allows us to recover the most substantial part of the solvent–solute interaction energy and approach a quantitative description of tautomeric equilibrium constants.

Acknowledgements

This work was performed using computational facilities of the Joint computational cluster of SSI “Institute for Single Crystals” and Institute for Scintillation Materials of National Academy of Sciences of Ukraine incorporated into Ukrainian National Grid. Authors are thankful to Dr Art Bochevarov (Schrödinger, LLC) for his valuable revision of the text.

Notes and references

1. N. Yu. Gorobets, A. V. Borisov, A. V. Silin, V. M. Nikitchenko and S. N. Kovalenko, Chem. Heterocycl. Compd., 2002, 38, 1389–1396.
2. L. Benmaktouf, H. Ammar, Y. Le Bigot and S. Abid, Synth. Commun., 2011, 41, 1017–1026.
3. C. N. O'Callaghan, T. B. H. McMurry, J. E. O'Brien, S. M. Draper and D. J. Wilcock, J. Chem. Soc., Perkin Trans. 1, 1996, 1067–1071.
4. J. O. Moon, J. W. Lee, M. G. Choi, S. Ahn and S.-K. Chang, Tetrahedron Lett., 2012, 53, 6594–6597.
5. J. A. Cabello, J. M. Campelo, A. Garcia, D. Luna and J. M. Marinas, J. Org. Chem., 1984, 49, 5195–5197.
6. A. A. Karasev, L. L. Lukatskaya, M. I. Rubtsov, Z. A. Sizova and A. O. Doroshenko, Russ. Chem. Bull., 2002, 51, 2070–2073.
7. P. E. Shynkarenko, S. V. Vlasov, S. M. Kovalenko, S. V. Shishkina, O. V. Shishkin and V. P. Chernykh, J. Heterocycl. Chem., 2010, 47, 800–806.
8. P. E. Shynkarenko, S. V. Vlasov, S. M. Kovalenko and V. P. Chernykh, J. Sulfur Chem., 2010, 31, 447–456.
9. S. Kovalenko, I. Bylov, K. Sytnik, V. Chernykh and Y. Bilokin, Molecules, 2000, 5, 1146–1165.
10. Y. V. Bilokin, M. V. Vasylyev, O. V. Branytska, S. M. Kovalenko and V. P. Chernykh, Tetrahedron, 1999, 55, 13757–13766.
11. S. M. Kovalenko, S. V. Vlasov and V. P. Chernykh, Synthesis, 2006, 2006, 847–852.
12. J. Volmajer, R. Toplak, I. Leban and A. M. L. Marechal, Tetrahedron, 2005, 61, 7012–7021.
13. M. Winterwerber, R. Geiger, U. Predoiu and H.-H. Otto, Monatsh. Chem., 2006, 137, 1441–1451.
14. O. S. Detistov, V. D. Orlov and I. O. Zhuravel, J. Heterocycl. Chem., 2012, 49, 883–892.
15. J. Volmajer, R. Toplak, S. Bittner, I. Leban and A. Majcen Le Marechal, Tetrahedron Lett., 2003, 44, 2363–2366.
16. H. Ammar, S. Abid, Y. Le Bigot and R. El Gharbi, Synth. Commun., 2011, 42, 799–810.
17. L. Capuano, G. Urhahn and A. Willmes, Chem. Ber., 1979, 112, 1012–1022.
18. C. N. O'Callaghan, J. Chem. Soc., Perkin Trans. 1, 1980, 1335–1337.
19. C. N. O'Callaghan, J. Chem. Soc., Perkin Trans. 1, 1981, 2273–2276.
20. J. Světík, F. Tureček and V. Hanuš, J. Chem. Soc., Perkin Trans. 1, 1988, 2053–2058.
21. S. A. S. Ghozlan and A. Z. A. Hassanien, Tetrahedron, 2002, 58, 9423–9429.
22. N. Y. Gorobets and V. V. Abakumov, Chem. Heterocycl. Compd., 2002, 38, 1518–1520.
23. N. Yu. Gorobets, V. V. Abakumov, A. V. Borisov and V. M. Nikitchenko, Chem. Heterocycl. Compd., 2004, 40, 334–342.
24. H. Turki, S. Abid, Y. Le Bigot, S. Fery-Forgues and R. El Gharbi, Synth. Commun., 2004, 34, 3553–3563.
25. A. V. Borisov, S. G. Dzhavakhishvili, I. O. Zhuravel, S. M. Kovalenko and V. M. Nikitchenko, J. Comb. Chem., 2006, 9, 5–8.
26. A. M. El-Sayed, Phosphorus, Sulfur Silicon Relat. Elem., 2006, 181, 2709–2723.
27. N. M. Evdokimov, A. S. Kireev, A. A. Yakovenko, M. Y. Antipin, I. V. Magedov and A. Kornienko, Tetrahedron Lett., 2006, 47, 9309–9312.
28. A. V. Borisov, N. Yu. Gorobets, S. A. Yermolayev, I. O. Zhuravel, S. M. Kovalenko and S. M. Desenko, J. Comb. Chem., 2007, 9, 909–911.
29. M. Kammoun, H. Turki, H. Ammar and R. El Gharbi, Synth. Commun., 2011, 42, 1677–1684.
30. I. E. Bylov, M. V. Vasylyev and Y. V. Bilokin, Eur. J. Med. Chem., 1999, 34, 997–1001.
31. J. A. Hadfield, V. H. Pavlidis, P. J. Perry and A. T. McGown, Anti-Cancer Drugs, 1999, 10, 591–596.
32. S. V. Ukhov, M. E. Kon'shin and T. F. Odegova, Pharm. Chem. J., 2001, 35, 364–365.
33. D. Grée, S. Vorin, V. L. Manthati, F. Caijo, G. Viault, F. Manero, P. Juin and R. Grée, Tetrahedron Lett., 2008, 49, 3276–3278.
34. S. V. Ukhov, B. Y. Syropyatov, V. V. Novikova, V. A. Balabash, A. S. Shustov and T. F. Odegova, Pharm. Chem. J., 2011, 45, 228–230.
35. E. Rajanarendar, M. Nagi Reddy, S. Rama Krishna, K. Rama Murthy, Y. N. Reddy and M. V. Rajam, Eur. J. Med. Chem., 2012, 55, 273–283.
36. N. Edraki, O. Firuzi, A. Foroumadi, R. Miri, A. Madadkar-Sobhani, M. Khoshneviszadeh and A. Shafiee, Bioorg. Med. Chem., 2013, 21, 2396–2412.
37. S. V. Ukhov, M. E. Kon'shin, V. V. Novikova and T. F. Odegova, Pharm. Chem. J., 2004, 38, 186–187.
38. A. A. El-Bindary, Spectrochim. Acta, Part A, 2001, 57, 49–54.
39. A. M. Amin, K. Abou Zid, N. A. Bayoumi and M. Abd El-hamid, J. Radioanal. Nucl. Chem., 2010, 283, 55–62.
40. K. Komatsu, Y. Urano, H. Kojima and T. Nagano, J. Am. Chem. Soc., 2007, 129, 13447–13454.
41. R. Rajagopal, V. U. Shenoy, S. Padmanabhan, S. Sequeira and S. Seshadri, Dyes Pigm., 1990, 13, 167–175.
42. V. V. Maslov, N. Yu. Gorobets, A. V. Borisov and V. M. Nikitchenko, J. Appl. Spectrosc., 2003, 70, 794–799.
43. Z. A. Syzova, A. O. Doroshenko, L. L. Lukatskaya, M. I. Rubtsov and A. A. Karasyov, J. Photochem. Photobiol., A, 2004, 165, 59–68.
44. A. Vasylevska, A. Karasyov, S. Borisov and C. Krause, Anal. Bioanal. Chem., 2007, 387, 2131–2141.
45. V. Kandavelu, H.-S. Huang, J.-L. Jian, T. C. K. Yang, K.-L. Wang and S.-T. Huang, Sol. Energy, 2009, 83, 574–581.
46. M. Fakhfakh, H. Turki, S. Fery-Forgues and R. El Gharbi, Dyes Pigm., 2010, 84, 108–113.
47. S.-T. Huang, J.-L. Jian, H.-Z. Peng, K.-L. Wang, C.-M. Lin, C.-H. Huang and T. C. K. Yang, Dyes Pigm., 2010, 86, 6–14.
48. D. Guo, T. Chen, D. Ye, J. Xu, H. Jiang, K. Chen, H. Wang and H. Liu, Org. Lett., 2011, 13, 2884–2887.
49. H. Turki, S. Abid, N. Saffon and S. Fery-Forgues, Dyes Pigm., 2012, 94, 81–87.
50. T.-I. Kim, H. Kim, Y. Choi and Y. Kim, Chem. Commun., 2011, 47, 9825–9827.
51. N. Yu. Gorobets, S. A. Yermolayev, T. Gurley, A. A. Gurinov, P. M. Tolstoy, I. G. Shenderovich and N. E. Leadbeater, J. Phys. Org. Chem., 2012, 25, 287–295.
52. F. A. Abu-Shanab, Y. M. Elkholy and M. H. Elnagdi, Heterocycl. Commun., 2001, 7, 183–192.
53. N. Yu. Gorobets, B. H. Yousefi, F. Belaj and C. O. Kappe, Tetrahedron, 2004, 60, 8633–8644.
54. N. Yu. Gorobets, Y. V. Sedash, S. V. Shishkina, O. V. Shishkin, S. A. Yermolayev and S. M. Desenko, ARKIVOC, 2009, 23–30.
55. F. Bondavalli, O. Bruno, E. Presti, G. Menozzi and L. Mosti, Synthesis, 1999, 1169–1174.
56. S. A. Yermolayev, N. Y. Gorobets, E. V. Lukinova, O. V. Shishkin, S. V. Shishkina and S. M. Desenko, Tetrahedron, 2008, 64, 4649–4655.
57. S. G. Dzhavakhishvili, N. Y. Gorobets, V. N. Chernenko, V. I. Musatov and S. M. Desenko, Russ. Chem. Bull., 2008, 57, 422–427.
58. S. A. Yermolayev, N. Yu. Gorobets, O. V. Shishkin, S. V. Shishkina and N. E. Leadbeater, Tetrahedron, 2011, 67, 2934–2941.
59. M. A. Vodolazhenko, N. Yu. Gorobets, S. A. Yermolayev, V. V. Musatov, V. A. Chebanov and S. M. Desenko, RSC Adv., 2012, 2, 1106–1111.
60. C. N. O'Callaghan, T. B. H. McMurry and J. E. O'Brien, J. Chem. Soc., Perkin Trans. 2, 1998, 425–429.
61. W. H. Perkin and R. Robinson, J. Chem. Soc., Trans., 1914, 105, 2376–2392.
62. C. N. O'Callaghan, T. B. H. McMurry and C. J. Cardin, J. Chem. Res., Synop., 1990, 132–133.
63. I. O. Zhuravel', S. M. Kovalenko, A. V. Ivachtchenko, V. P. Chernykh and P. E. Shinkarenko, J. Heterocycl. Chem., 2004, 41, 517–524.
64. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision D.01, Gaussian, Inc., Wallingford CT, 2004.
65. P. Sinha, S. E. Boesch, C. Gu, R. A. Wheeler and A. K. Wilson, J. Phys. Chem. A, 2004, 108, 9213–9217.
66. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094.
67. R. Dennington, T. Keith and J. Millam, GaussView, Version 5, Semichem Inc., Shawnee Mission, KS, 2009.
68. G. Gilli and P. Gilli, J. Mol. Struct., 2000, 552, 1–15.
69. Y. Gu, T. Kar and S. Scheiner, J. Am. Chem. Soc., 1999, 121, 9411–9422.
70. Advances in Molecular Structure Research, ed. M. Hargittai and I. Hargittai, JAI Press Inc., Stamford, CT, 2000.
71. R. J. Abraham and M. Mobli, Magn. Reson. Chem., 2007, 45, 865–877.
72. E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173.
73. A. Robertazzi and J. A. Platts, Inorg. Chem., 2005, 44, 267–274.
74. M. P. Waller, A. Robertazzi, J. A. Platts, D. E. Hibbs and P. A. Williams, J. Comput. Chem., 2006, 27, 491–504.
75. I. Mata, I. Alkorta, E. Espinosa and E. Molins, Chem. Phys. Lett., 2011, 507, 185–189.
76. V. G. Kontogianni, P. Charisiadis, A. Primikyri, C. G. Pappas, V. Exarchou, A. G. Tzakos and I. P. Gerothanassis, Org. Biomol. Chem., 2013, 11, 1013–1025.

---

Footnote

† Electronic supplementary information (ESI) available: Tables S1–S33 contain selected geometrical parameters, structures and relative stability for all structures; intra- and intermolecular bond lengths and estimation of the bond energies for the most stable conformers. See DOI: 10.1039/c6ra08873b

---