Structural, magnetic and theoretical investigations on the magnetocaloric properties of La0.7Sr0.25K0.05MnO3 perovskite
S. El Kossi*a,
J. Dhahria and
E. K. Hlilb
aLaboratoire de La Matière Condensée et des Nanosciences, Département de Physique, Faculté des Sciences University de Monastir, 5019, Tunisia. E-mail: safwene666@hotmail.com; Fax: +216 73500278; Tel: +216 53180481
bInstitut Néel, CNRS et Université Joseph Fourier, BP 166, 38042 Grenoble, France
First published on 27th June 2016
Abstract
The La0.7Sr0.25K0.05MnO3 (LSKMO0.05) manganite compound was synthesized by the solid state reaction method. X-ray diffraction analysis revealed that this sample crystallizes in the distorted rhombohedral system with the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group. The magnetic study showed a second order paramagnetic (PM)-ferromagnetic (FM) transition at the Curie temperature TC = 332 K. In addition, isothermal measurements of magnetization allowed us, through thermodynamic Maxwell relations, to determine the magnetic entropy change (ΔSM). The maximum magnetic entropy change (ΔSmax) and the relative cooling power (RCP) were found to be, respectively, 2.37 J kg−1 K−1 and 102 J kg−1 for a 2 T magnetic field change along with a negligible hysteresis loss, making this material a promising candidate for magnetic refrigeration. In order to eliminate the drawbacks due to the use of multistep nonlinear fitting in a conventional manner, the field dependence of magnetic entropy change was applied to study the critical behavior. As expected, our results are consistent with the values derived for the 3D-Heisenberg model.
c space group. The magnetic study showed a second order paramagnetic (PM)-ferromagnetic (FM) transition at the Curie temperature TC = 332 K. In addition, isothermal measurements of magnetization allowed us, through thermodynamic Maxwell relations, to determine the magnetic entropy change (ΔSM). The maximum magnetic entropy change (ΔSmax) and the relative cooling power (RCP) were found to be, respectively, 2.37 J kg−1 K−1 and 102 J kg−1 for a 2 T magnetic field change along with a negligible hysteresis loss, making this material a promising candidate for magnetic refrigeration. In order to eliminate the drawbacks due to the use of multistep nonlinear fitting in a conventional manner, the field dependence of magnetic entropy change was applied to study the critical behavior. As expected, our results are consistent with the values derived for the 3D-Heisenberg model.
1. Introduction
Magnetic refrigeration based on the magnetocaloric effect (MCE) is a promising alternative to conventional gas compression refrigeration. This is thanks to its high efficiency, small volume, energy saving and ecological cleanliness; in fact, this technology does not use toxic gases that can negatively influence the ozone layer.1,2 Therefore, new and improved promising magnetic materials are one of the cornerstones in the development of room temperature magnetic refrigeration.In the context of MR applications, several materials with giant magnetic entropy changes have been proposed. Among these materials we can cite Gd5Si4−xGex,3 MnAs1−xSbx4 and La(Fe1−xSix)13.5 They undergo a simultaneous first-order structural and magnetic-phase transition that is believed to be responsible for the large MCE. These compounds exhibit a MCE about twice as large as that exhibited by gadolinium, the best known magnetic refrigerant material for near room-temperature applications.1 Further efforts to find new materials, especially the materials without rare-earth elements, have revealed that some of perovskite manganese oxides are also expected to be promising candidates in magnetic refrigeration technology.6,7 This is attributed to their colossal magnetoresistance, as well as the large change in temperature in adiabatic conditions under moderate external magnetic field. Perovskite manganites with a general formula R1−xTxMnO3 where R is a rare earth atom (La, Pr, Nd, etc.) and T is an alkaline earth element (Sr, Ca, Ba, etc.), present a wide spectrum of structural and functional phases associated to the complex interplay between charge, spin, orbit and structural aspects which are sensitive to the arrangement of the 3d electrons of Mn in their orbit.8 Recent studies suggest that multifunctional behavior can be achieved through a careful chemical manipulation explained by the double-exchange (DE) mechanism and the strong electron-phonon coupling caused by lattice polarons and dynamic Jahn–Teller (JT) distortions.9 Following this mechanism, a number of works reported on the MCE in lanthanum manganites wherein a large magnetocaloric effect has been found. Among the lanthanum-based manganites, the strontium-doped lanthanum manganites (La1−xSrxMnO3, LSMO) have secured a prominent position based on the high potential for magnetic sensor applications magnetoresistance effect and the MCE as they possess high magnetic moments.10 These manganites exhibit a metal-to-insulator transition accompanied by a ferromagnetic-to-paramagnetic transition near the Curie temperature TC, which directed the focus towards magnetic entropy studies. Experimentally, it has been revealed that the La0.67Sr0.33MnO3 compound is characterized by a maximum magnetic entropy change of ΔSMax equal to 2.68 J kg−1 K−1 at a 370 K and under a magnetic field of 2 T which is beneficial for technological applications.11 The new investigation field is focused on the manganites doped with monovalent elements. In fact, the substitution of the monovalent cations for the rare earth cations in manganites is of a particular interest. This is because it leads to converting twice more Mn3+ to Mn4+ ions to give rise to the double exchange interactions, which are the origin of the ferromagnetic character and the CMR effect. Therefore, even a small amount of doping results in a large number of charge carriers and as a consequence an increase in the conductivity can be achieved and the crystal structure may be modified depending on the radius of monovalent ions. The Curie temperature is, therefore, expected to be reduced as compared to that reported for the parent undoped manganite. Besides, our research group has widely studied the effect of monovalent elements on the physical properties of La0.67Sr0.33MnO3. In addition, we have found an important value of ΔSMax = 2.32 J kg−1 K−1 and TC = 363 K under a magnetic field of 2 T in the La0.7Sr0.25Na0.05MnO3 sample.12 These values of ΔSMax are significant but the Curie temperatures are higher at room temperature. To get more insights into the effect of the monovalent cations on manganite, we turn our attention to potassium-doped perovskite manganites to see if it improves the magnetic and magnetocaloric properties of our sample.
The purpose of this work is to investigate in details the field induced magnetic phase transition and the MCE of La0.7Sr0.25K0.05MnO3 compound and its possibility for application as an active magnetic refrigerant (AMR) material. A phenomenological model was used for the simulation of the dependence of magnetization on temperature variation to predict the magnetocaloric properties such as magnetic entropy change, heat capacity change, and relative cooling power.
2. Experimental details
The polycrystalline sample L0.7Sr0.25K0.05MnO3 was synthesized by solid state reaction. Pure (≥99.99%) raw powders with appropriate amounts of La2O3, SrCO3, K2CO3 and MnO2 were thoroughly ground and mixed, then pressed into pellets. These were calcined at several processing steps with increasing temperatures from 900 °C to 1100 °C and with intermediate grindings and pelletizations. The product was then sintered at 1200 °C for 24 h in ambient atmosphere. Finally, these pellets were rapidly quenched to room temperature in order to keep the structure at an annealing temperature.13Phase purity, homogeneity and crystal properties were determined by powder X-ray diffraction (XRD) data, recorded at room temperature on a PANalytical X'PERT Pro MPD diffractometer, using θ/2θ Bragg–Brentano geometry with diffracted beam monochromatized CuKα radiation (λ = 1.5406 Å). The surface morphology was investigated by a field-emission scanning electron microscopy (SEM) attached with energy dispersive analysis through X-rays (EDAX). Magnetizations (M) vs. temperature (T) were measured using BS1 and BS2 magnetometers developed in Louis Néel Laboratory of Grenoble. BS1 (300–900 K) and BS2 (1.5–300 K) magnetometers are used respectively for magnetic measurements at high and low temperatures equipped with a super conducting coil. These two instruments are automated by a computer system that allows the registration of digital data for each successive measurement. Magnetization isotherms were measured in the range of 0–5 T and with a temperature interval of 3 K in the vicinity of Curie temperature (TC). These isothermals were corrected by a demagnetization factor D that was determined by a standard procedure from low-field dc magnetization measurement at low temperatures (H = Happ-DM). Finally, the magnetocaloric effect (MCE) was characterized by an isothermal change of the magnetic entropy and the adiabatic change of temperature. In fact, the magnetocaloric effect was estimated in terms of isothermal magnetic entropy change (ΔSM) using M–μ0H-T data and Maxwell's relation:14,15
 | (1) |
On the other hand, the relative cooling power RCP was calculated using the relation:
 | (2) |
3. Results and discussion
3.1. X-ray analysis
Fig. 1 shows the room temperature X-ray diffraction (XRD) pattern of the synthesized LSKMO0.05 sample with a fit of whole profile. The diffraction peaks are sharp, indicating well crystallized phases. No impurity phases were detected within the X-ray diffraction limits.The structural parameters of the samples are refined by the standard Rietveld technique16 using the FullProf program.17 As can be seen from this figure, the sample is of a single phase without any detectable secondary phase and can be indexed according to the rhombohedral perovskite structure with a space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c (no. 167), in which the (La, Sr, K) atoms are at 6a (0, 0, 1/4) positions, Mn at 6b (0, 0, 0) and O at 18e (x, 0, 1/4). The difference observed between the intensities of the measured and calculated diffraction pattern can be attributed to the existence of a preferential orientation of the crystallites in the sample. The quality of the agreement is evaluated through the adequacy of the fit indicator χ2. The related results are listed in Table 1. The structural stability of LSKMO0.05 sample was estimated by Goldschmidt's tolerance factor tG, which has been widely admitted as a criterion for the formation of a perovskite structure, expressed as follows:18
c (no. 167), in which the (La, Sr, K) atoms are at 6a (0, 0, 1/4) positions, Mn at 6b (0, 0, 0) and O at 18e (x, 0, 1/4). The difference observed between the intensities of the measured and calculated diffraction pattern can be attributed to the existence of a preferential orientation of the crystallites in the sample. The quality of the agreement is evaluated through the adequacy of the fit indicator χ2. The related results are listed in Table 1. The structural stability of LSKMO0.05 sample was estimated by Goldschmidt's tolerance factor tG, which has been widely admitted as a criterion for the formation of a perovskite structure, expressed as follows:18
 | (3) |
Phase R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) C C |
|
|---|---|
| Structural model cell parameters | |
| a (Å) | 5.524 (2) |
| c (Å) | 13.376 (1) |
| Cell volume (Å3) | 353.52 (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Isotropic thermal parameters | |
| B(La/K/Sr) (Å2) | 0.24 (2) |
| B(Mn) (Å2) | 0.73 (3) |
| B(O) (Å2) | 0.47 (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Discrepancy factors | |
| RP (%) | 6.8 |
| Rwp (%) | 6.4 |
| RF (%) | 5.2 |
| χ2 | 2.7 |
In general, the perovskite structure is stable in the region 0.75 < tG < 1.06, and the symmetry is higher as the tG value is closer to 1. This parameter is an indication of how far the atoms can move from the ideal packing and be still belonging to the perovskite structure. In the present study, the tolerance factor of LSKMO0.05 is calculated from Shannon's ionic radii rLa3+ = 1.22 Å, rSr2+ = 1.44 Å, rK+ = 1.55 Å, rMn3+ = 0.65 Å, rMn4+ = 0.53 Å and rO2− = 1.4 Å (ref. 19) and it is found to be 0.963 which improves a stable perovskite structure.
The inset of Fig. 2 shows the scanning electron microscopy (SEM) photograph for the LSKMO0.05 sample. We can see that the grains exhibit spheroid-like shapes and a good connectivity between each other. Using the linear intercept method, the grain size was estimated to be mostly within 208 nm. In order to check the cationic composition of the sample, the Energy Dispersive X-ray Analysis (EDAX) was performed at room temperature (Fig. 2). EDAX plot reveals the presence of all expected chemical elements introduced in the starting oxide powders, which confirms that there was no loss of any integrated element during the process of preparation.
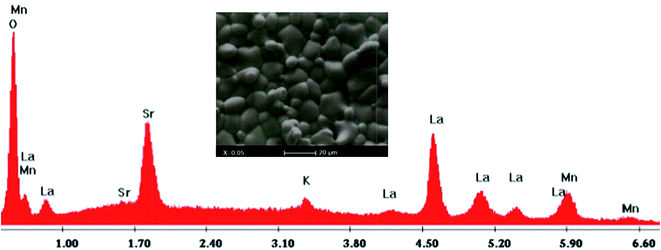 | ||
| Fig. 2 Plot of EDX analysis of chemical species of La0.7Sr0.25K0.05MnO3. The inset shows typical scanning electron micrography (SEM). | ||
3.2. Magnetization investigation
Magnetization measurements versus temperature, recorded under a magnetic field of 0.05 T, are shown in Fig. 3a. We observe a sharp transition from high-temperature paramagnetic state to low temperature ferromagnetic state. This curve reveals a strong variation of magnetization around the ferromagnetic Curie temperature (TC = 332 K) defined as the inflection point of dM/dT curve (inset of Fig. 3a). It indicates that there is a possible large magnetic entropy change. For a further understanding of the magnetic interaction at a high temperature, we have investigated the temperature dependence of the inverse magnetic susceptibility χ for 0.05 T (Fig. 3b). For a ferromagnet, it is well known that in the PM region, the relation between χ and the temperature T should follow the Curie–Weiss law, i.e. χ = C/T − θCW, where θCW is the Weiss temperature and C is the Curie constant defined as:
 | (4) |
From the slope of the linear 1/χ vs. T curve (see Fig. 3b), the experimental effective paramagnetic moments can be determined and the temperature at which 1/χ intercepts the temperature axis is the Curie Weiss temperature θCW. Assuming orbital momentum to be quenched in Mn3+ and Mn4+, the theoretical paramagnetic effective moment μtheff can be written as:
 | (5) |
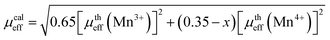 | (6) |
From the high temperature linear fit, the effective magnetic moment evaluated is equal to 3.83 μB, which is slightly smaller than the calculated effective paramagnetic moment 4.04 μB. The discrepancy between the experimental and the theoretical values implies that some short-range FM couplings might have been developed in the PM region contributing to the additional magnetic moments. This phenomenon is generally termed as “magnetic phase separation” and has been extensively reported in manganites.21 It can also be remarked that the paramagnetic Curie–Weiss temperatures θCW value is slightly higher than TC. Generally, the difference between θCW and TC (θCW > TC) depends on the substance and is associated with the presence of short-range magnetic interaction ordered slightly above TC, which may be related to the presence of a magnetic inhomogeneity.22
To evaluate the MCE of the present sample, the isothermal magnetic field dependence of magnetization M–μ0H was measured at different temperatures in the range of 296–398 K, as shown in Fig. 4a (magnetic field was varying from 0 to 5 T). We found a clear ferromagnetic behavior at all temperatures. This reveals a strong variation of magnetization around Curie temperature indicating that there is a possible large magnetic entropy change associated with the FM-PM transition temperature occurring at TC. Fig. 4b show the Arrott plot M2 vs. μ0H/M. However, all the curves in the Arrott plots are nonlinear and show upward curvature even at high field, indicating that the present phase transition will not satisfy the mean field theory. Moreover, the concave downward curvature clearly indicates a second order phase transition according to the criterion suggested by Banerjee.23 According to the criterion, the negative and positive slopes of μ0H/M vs. M2 isotherms curves (Arrott plots) suggest a first-order and a second-order phase transition, respectively. For the present compound, a positive slope of the Arrott plots can be observed, which indicates the second-order nature of phase transition.
 | ||
| Fig. 4 (a) Isothermal magnetization versus magnetic field M vs. μ0H at different temperatures for La0.7Sr0.25K0.05MnO3 sample. (b) The standard Arrott plot M2 versus μ0H/M. | ||
3.3. Theoretical considerations
 | (7) |
 ; B is the magnetization sensitivity dM/dT at ferromagnetic state before transition;
; B is the magnetization sensitivity dM/dT at ferromagnetic state before transition;  is the magnetization sensitivity dM/dT at Curie temperature TC and
is the magnetization sensitivity dM/dT at Curie temperature TC and  .
.
Differentiating eqn (7) gives:
 | (8) |
Using eqn (1) and (8), the magnetic entropy change of a magnetic system under adiabatic magnetic field variation from 0 to final value μ0 Hmax can be rewritten as follows:
 | (9) |
The presence of a large magnetic entropy change is accredited to a high magnetic moment interaction and a rapid change of magnetization at TC. The result of eqn (9) is a maximum magnetic entropy change ΔSmax (where T = TC) can be evaluated as the following equation:
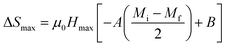 | (10) |
Furthermore, the determination of full-width at half-maximum δTFWHM can be performed as follows:
 | (11) |
Relative cooling power (RCP) is a useful parameter, which decides the effectiveness of magnetocaloric materials based on the magnetic entropy change.25 The RCP is defined as the product of the maximum magnetic entropy change ΔSMax and full width at half maximum (δTFWHM) in ΔSM (T) curve.
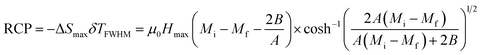 | (12) |
The heat capacity ΔCP,H can be calculated, from the magnetic contribution to the entropy change induced in the material, by the following expression:26
 | (13) |
From eqn (9)  can be inferred as follows:
can be inferred as follows:
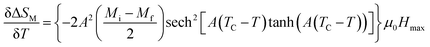 | (14) |
From eqn (13) and (14), ΔCP,H can be rewritten as:
| ΔCP,H = −TA²(Mi − Mf)sech2[A(TC − T)] tanh[A(TC − T)]μ0Hmax | (15) |
From this phenomenological model, ΔSM, δTFWHM, RCP and ΔCP,H can be simply evaluated for La0.7Sr0.25K0.05MnO3 under magnetic field variation.
| μ0H(T) | TC (K) | Mf (emu g−1) | Mi (emu g−1) | B (emu g−1 K−1) | SC (emu g−1 K−1) |
|---|---|---|---|---|---|
| 1 | 332.3 | 62.3 | 3.3 | −0.014 | −1.54 |
| 2 | 335.5 | 64.1 | 6.2 | −0.033 | −1.24 |
| 3 | 336.7 | 67.5 | 9.6 | −0.036 | −0.05 |
| 4 | 337.6 | 68.7 | 11.8 | −0.045 | −0.92 |
| 5 | 338.2 | 69.4 | 14.7 | −0.058 | −0.79 |
 | ||
| Fig. 6 Magnetization versus temperature for the La0.7Sr0.25K0.05MnO3. The solid lines are modeled results and symbols represent experimental data. | ||
Fig. 7 shows the dependence of the magnetic entropy change on temperature for different applied magnetic fields for La0.7Sr0.25K0.05MnO3 sample. The solid lines are modeled results and the symbols represent experimental data. The results of calculations are in accordance with the experimental results. It is interesting to note that the maximum of the magnetic entropy change is obtained near Curie temperature (TC = 332 K) of the sample. It is found to be positive in the entire temperature range for all magnetic fields, which confirmed the ferromagnetic character.28 We can see from Fig. 7 that the magnitude of ΔSM increases with increasing the strength of μ0H and reaches a maximum value of 1.34 J kg−1 K−1 and 4.85 J kg−1 K−1 under a magnetic field change of μ0H = 1 T and μ0H = 5 T, respectively. In fact, the intensity of the magnetic field plays an important role in magnetic cooling. The maximum magnetic entropy change ΔSmax exhibits a linear rise with increasing field, which indicates a much larger entropy change to be expected at a higher magnetic field, signifying, therefore, the effect of spin-lattice coupling associated to changes in the magnetic ordering process in the sample.29 Another interesting feature to be noted is that for the LSKMO0.05 sample, the maximum of the magnetic entropy, 2.37 J kg−1 K−1 for a 2 T applied magnetic field, which is about 45% of the pure Gd30 is larger than the ΔSmax value of many perovskite materials (Table 3). These results clearly suggest that this compound could be a suitable candidate as a working material in refrigeration devices at near room temperature. To explain the large magnetic entropy change in perovskite manganites, Zener's double exchange model is strongly recommended.31 The effect of the double-exchange interaction between Mn3+ and Mn4+ ions would be closely related to the change in Mn3+/Mn4+ ratio, under the doping process. In addition, Guo et al. suggest that the large magnetic entropy change in perovskite manganites could be originating from the spin-lattice coupling in the magnetic ordering process.32 Because of the strong coupling spin and lattice, a significant change in the lattice accompanying the magnetic transition in perovskite manganites has been observed.33,34 The lattice structural change in 〈Mn–O〉 bond distance as well as in the 〈Mn–O–Mn〉 bond angle would in turn favor the spin ordering. As a result, a more abrupt variation of magnetization near TC occurs, which leads to a large magnetic entropy change, resulting in a large MCE.
| Materials | μ0H (T) | −ΔSM (J kg−1 K−1) | δTFWHM (K) | RCP (J kg−1) | ΔCP,Hmax (J kg−1 K−1) | ΔCP,Hmin (J kg−1 K−1) | Refs. |
|---|---|---|---|---|---|---|---|
| La0.7Sr0.25K0.05MnO3 | 1 | 1.34 | 36.05 | 48.32 | 5.79 | −5.48 | Present |
| 2 | 2.37 | 44.64 | 105.37 | 11.64 | −10.97 | Present | |
| 3 | 3.15 | 51.54 | 162.38 | 19.56 | −18.41 | Present | |
| 4 | 4.04 | 55.38 | 223.75 | 27.66 | −25.93 | Present | |
| 5 | 4.85 | 58.15 | 282.03 | 34.81 | −32.45 | Present | |
| Gd | 2 | 5.5 | — | 164 | — | — | 47 |
| La0.95Ag0.05MnO3 | 1 | 1.1 | — | 44 | — | — | 48 |
| La0.925Na0.075MnO3 | 1 | 1.32 | 93 | — | — | 49 | |
| Pr0.55Sr0.4K0.05MnO3 | 2 | 2.19 | — | 87 | 50 | ||
| La0.8Na0.05K0.15MnO3 | 2 | 2.2 | 107 | 51 | |||
| Pr0.6Sr0.35Na0.05MnO3 | 2 | 1.84 | 92 | 52 | |||
| La0.7Sr0.25Na0.05MnO3 | 2 | 2.32 | 82 | 12 | |||
| La0.7Ca0.3MnO3 | 3 | 2.2 | 55 | 53 | |||
| La0.60Y0.07Ca0.33MnO3 | 3 | 1.46 | 140 | 54 | |||
| Nd0.55Sr0.45MnO3 | 3 | 3.12 | 71 | 55 | |||
| Gd | 5 | 9.5 | 410 | 1 | |||
| La0.7Sr0.3Mn0.93Fe0.07O3 | 5 | 4 | 255 | 11 | |||
| La0.7Sr0.2Ag0.1MnO3 | 5 | 4 | 244 | 56 | |||
| La0.7Sr0.25Na0.05MnO3 | 5 | 4.34 | 298 | 12 | |||
| La0.6Pr0.1Sr0.3MnO3 | 5 | 3.32 | 227 | 57 |
Another relevant quantity to evaluate the applicability of a magnetocaloric material is the relative-cooling-power (RCP), which is defined as:35
| RCP = −ΔSmax × δTFWHM | (16) |
Fig. 8 shows the temperature dependence of ΔCp under different field variations for the sample calculated from ΔSM − T curves of Fig. 7 by using relation:
 | ||
| Fig. 8 Heat capacity changes (ΔCp) as function of temperature for La0.7Sr0.25K0.05MnO3 in different applied magnetic field variations. | ||
The ΔCp undergoes a sudden change from positive to negative around TC with a positive value above TC and a negative value below TC. The positive or negative values of ΔCp closely above or below TC may strongly alter the total specific heat. Furthermore, the maximum and minimum values of specific heat change for this sample are estimated and summarized in Table 3. Finally, in this model, a few necessary parameters are required and the processing time for the simulation is limited. The used procedure does not add any supplementary computational effort to the numerical simulation and it is suitable to be coupled with field computation.
Based on the standard scaling theory,36 it has been found that the magnetic materials with a second order phase transition follow a universal behavior as far as the MCE variation is concerned. However, Franco et al.37 prescribed that the measured curves of ΔSM(T) at different applied magnetic fields should collapse on to the same universal curve. This procedure was performed by normalizing the magnetic entropy change curves ΔSM with respect to their peak ΔSmax and rescaling the temperature axis using a two reference temperatures in a different way below and above TC. A new temperature variable θ is defined by the following expression:
 | (17) |
The temperatures Tr1 and Tr2 correspond to the temperatures for which ΔSM(Tr) = 0.5ΔSmax. Noticeably, from Fig. 9 the scaled curves overlap into the same curve; indicating the validity of our data treatment for compounds with a second-order transition. Furthermore, the universal curve can be well fitted by a Lorentz distribution function:
 | (18) |
 | ||
| Fig. 9 The master curve behavior of the curve as a function of the rescaled temperature. The inset shows the collapse of the experimental data onto the average curve: the solid line is the fit to eqn (18). | ||
Referring to eqn (18), just three main parameters are required to characterize the entropy change: the magnitude (ΔSmax), the position of the peak (TC) and two reference temperatures Tcold and Thot, where Tcold < TC and Thot > TC. These parameters can be considered as system resources. Indeed, the “real” ΔSM (T) can be translated from ΔS′ (θ) by the knowledge of these parameters. Thus, incomplete ΔSM (T) curves, which are experimentally determined from a small temperature span in the vicinity of TC for the isothermal magnetization measurements, can be easily transformed into complete curves. This is a helpful tool for the evaluation of material properties such as the refrigerant capacity (RC). Furthermore, engineers can use this function to analyze the influence of material parameters on the design of a magnetic refrigerator.
Besides the urgent need for low cost MCE materials, the analysis of the critical behavior provides an important reference point since it is directly related to the MCE.38,39 It has been recently experimentally shown and theoretically demonstrated, based on Arrott–Noakes equation of state, that the field dependence of the magnetic entropy change can be expressed by the following relations:40,41
 | (19) |
 | (20) |
In the particular case of T = TC or at the temperature of the peak entropy change, the exponent n becomes field independent:
 | (21) |
This can be transformed using the relation:42 βδ = β + γ
 | (22) |
On the basis of a mean field approach, the field dependence of the magnetic entropy change at the Curie temperature corresponds to n = 2/3.43,44 However, by fitting the data of ΔSM vs. μ0H on the ln–ln scale, the values of n obtained from the slope around TC (Fig. 10a) are 0.60. These values perfectly agree with the values reported in other soft magnetic materials.45 On the other hand, the field dependence of RCP for our samples can be expressed as a power law by taking the field dependence of entropy change ΔSM and reference temperature into consideration:
 | (23) |
4. Conclusion
The results of the present investigation concerning the structural, magnetic and magnetocaloric properties of La0.7Sr0.25K0.05MnO3 manganite can be summarized as follows. The single phase of LSKM0.05 compound, synthesized using the solid state reaction method, crystallizes in the rhombohedral structure with R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group. This sample exhibits a second-order ferromagnetic to paramagnetic phase transition around Curie temperature TC = 332 K. A large magnetocaloric effect is observed under an applied magnetic field of 2 T, and the maximum of the magnetic entropy change ΔSmax is found to be 2.37 J kg−1 K−1, which is comparable to other manganites. The dependence of magnetization on temperature variation for LSKM0.05 upon different magnetic fields was simulated. In general, this allows predicting the magnetocaloric properties such as magnetic entropy change, full-width at half-maximum, relative cooling power and magnetic specific heat change, upon different magnetic field variations. The obtained results indicate that the La0.7Sr0.25K0.05MnO3 manganite could be a potential candidate for magnetic refrigeration applications at room temperature.
c space group. This sample exhibits a second-order ferromagnetic to paramagnetic phase transition around Curie temperature TC = 332 K. A large magnetocaloric effect is observed under an applied magnetic field of 2 T, and the maximum of the magnetic entropy change ΔSmax is found to be 2.37 J kg−1 K−1, which is comparable to other manganites. The dependence of magnetization on temperature variation for LSKM0.05 upon different magnetic fields was simulated. In general, this allows predicting the magnetocaloric properties such as magnetic entropy change, full-width at half-maximum, relative cooling power and magnetic specific heat change, upon different magnetic field variations. The obtained results indicate that the La0.7Sr0.25K0.05MnO3 manganite could be a potential candidate for magnetic refrigeration applications at room temperature.
Acknowledgements
This work is supported by the Tunisian National Ministry of Higher Education, Scientific Research, and the French Ministry of Higher Education and Research of CMCU 10G1117 collaboration.References
- K. A. Gschneidner Jr, V. K. Pecharsky and A. O. Tsokol, Rep. Prog. Phys., 2005, 68, 1479 CrossRef.
- V. K. Pecharsky and K. A. Gschneidner Jr, Adv. Mater., 2001, 13, 683 CrossRef CAS.
- V. K. Pecharsky and K. A. Gschneidner, Phys. Rev. Lett., 1997, 78, 44941 CrossRef.
- H. Wada and Y. Tanabe, Appl. Phys. Lett., 2001, 79, 3302 CrossRef CAS.
- A. Fujita and K. Fukamichi, IEEE Trans. Magn., 1999, 35, 1796 Search PubMed.
- M. Khlifi, E. Dhahri and E. K. Hlil, J. Appl. Phys., 2014, 115, 193905 CrossRef.
- S. Choura Maatar, R. M'nassri, W. Cheikhrouhou Koubaa, M. Koubaa and A. Cheikhrouhou, J. Solid State Chem., 2015, 225, 83 CrossRef CAS.
- C. Zener, Phys. Rev., 1951, 82, 403 CrossRef CAS.
- P. T. Phong, L. V. Bau, L. C. Hoan, D. H. Manh, N. X. Phuc and I.-J. Lee, J. Alloys Compd., 2015, 645, 243–249 CrossRef CAS.
- A. N. Ulyanov, G. V. Gusakov, V. A. Borodin, N. Y. Starostyuk and A. B. Mukhin, Solid State Commun., 2001, 118, 103–105 CrossRef CAS.
- A. Rostamnejadi, M. Venkatesan, P. Kameli, H. Salamati and J. M. D. Coey, J. Magn. Magn. Mater., 2011, 323, 2214 CrossRef CAS.
- S. E. L. Kossi, S. Ghodhbane, S. Mnefgui, J. Dhahri and E. K. Hlil, J. Magn. Magn. Mater., 2015, 395, 134 CrossRef CAS.
- S. B. Desu, J. Am. Ceram. Soc., 1990, 73, 3407 CrossRef CAS.
- V. K. Pecharsky, K. A. Gschneidner, A. O. Percharsky and A. M. Tishin, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 144406 CrossRef.
- A. Szewczyk, M. Gutowska, B. Dabrowski, T. Plackowski, N. P. Danilova and Y. P. Gaidukov, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 224432 CrossRef.
- H. M. Rietveld, A profile refinement method for nuclear and magnetic structures, J. Appl. Crystallogr., 1969, 2, 65–71 CrossRef CAS.
- D. B. Wiles and R. A. Young, J. Appl. Crystallogr., 1981, 14, 149 CrossRef CAS.
- V. Goldschmidt, Geochemistry, Oxford University Press, London, 1958 Search PubMed.
- R. D. Shanon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751 CrossRef.
- C. Kittel, Introduction to Solid State Physics, Wiley, New York, 6th edn, 1986, pp. 404–406 Search PubMed.
- M. H. Phan, M. B. Morales, N. S. Bingham, H. Srikanth, C. L. Zhang and S. W. Cheong, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 094413 CrossRef.
- T. I. Arbuzova, V. I. Voronin, B. A. Gizhevskil, S. V. Naumov and V. L. Arbuzov, Phys. Solid State, 2010, 52, 1217–1226 CrossRef CAS.
- B. K. Banerjee, Phys. Lett., 1964, 12, 16–17 CrossRef.
- Elementary Solid State Physics by Ali Omer.
- M. A. Hamad, Phase Transitions, 2012, 85, 159–168 CrossRef CAS.
- T. Samanta, I. Das and S. Banerjee, Appl. Phys. Lett., 2007, 91, 082511 CrossRef.
- M.-H. Phan, S.-C. Yu, N. Hwi Hur and Y.-H. Jeong, J. Appl. Phys., 2004, 96, 1154 CrossRef CAS.
- A. Dhahri, M. Jemmali, E. Dhahri and M. A. Valente, J. Alloys Compd., 2015, 638, 221 CrossRef CAS.
- R. Skini, M. Khlifi, M. Wali, E. Dhahri and E. K. Hlil, J. Magn. Magn. Mater., 2014, 324, 217 CrossRef.
- E. Brück, O. Tegus, D. T. C. Thanh and K. H. J. Buschow, J. Magn. Magn. Mater., 2007, 310, 2793 CrossRef.
- Z. M. Wang, G. Ni, Q. Y. Xu, H. Sang and Y. W. Du, J. Appl. Phys., 2001, 90, 5689 CrossRef CAS.
- Z. B. Guo, Y. W. Du, J. S. Zhu, H. Huang, W. P. Ding and D. Feng, Phys. Rev. Lett., 1997, 78, 1142 CrossRef CAS.
- P. G. Radaelli, D. E. Cox, M. Marizio, S. W. Sheong, P. E. Schiffer and A. P. Ramirez, Phys. Rev. Lett., 1995, 75, 4488 CrossRef CAS PubMed.
- W. Chen, W. Zhong, D. I. Hou, R. W. Gao, W. C. Feng, M. G. Zhu and Y. W. Du, J. Phys.: Condens. Matter, 2002, 14, 11889–11896 CrossRef CAS.
- K. A. Gschneidner Jr and V. K. Pecharsky, Annu. Rev. Mater. Res., 2000, 30, 387 CrossRef.
- V. Franco, A. Conde, J. M. Romero-Enrique and J. S. Blázquez, J. Phys.: Condens. Matter, 2008, 20, 285207 CrossRef.
- B. Biel, F. J. Garcia-Vidal, A. Rubio and F. Flores, Phys. Rev. Lett., 2005, 95, 266801 CrossRef PubMed.
- V. Franco, R. Caballero-Flores, A. Conde, K. E. Knipling and M. A. Willard, J. Appl. Phys., 2011, 109, 07A905 Search PubMed.
- J. Fan, L. Pi, L. Zhang, W. Tong, L. Ling, B. Hong, Y. Shi, W. Zhang, D. Lu and Y. Zhang, Appl. Phys. Lett., (2011), 98, 072508 Search PubMed.
- V. Franco, J. S. Blazquez and A. Condea, Appl. Phys. Lett., 2006, 89, 222512 CrossRef.
- L. Xu, J. Fan, Y. Shi, Y. Zhu, K. Bärne, C. Yang and D. Shi, Europhys. Lett., 2015, 112, 17005 CrossRef.
- B. Widom, J. Chem. Phys., 1965, 43, 3898 CrossRef.
- M. Pekala, J. Appl. Phys., 2010, 108, 113913 CrossRef.
- H. Oesterreicher and F. T. Parker, J. Appl. Phys., 1984, 55, 4334 CrossRef CAS.
- D. N. H. Nam, N. V. Dai, L. V. Hong, N. X. Phuc, S. C. Yu, M. Tachibana and E. Takayama-Muromachi, J. Appl. Phys., 2008, 103, 043905 CrossRef.
- P. Zhang, P. Lampen, T. L. Phan, S. C. Yu, T. D. Thanh, N. H. Dan, V. D. Lam, H. Srikanth and M. H. Phan, J. Magn. Magn. Mater., 2013, 348, 146 CrossRef CAS.
- S. Y. Dan'kov, A. M. Tishin, V. K. Pecharsky and K. A. Gschneidner Jr, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 3478 CrossRef.
- T. Tang, K. M. Gu, Q. Q. Cao, D. H. Wang, S. Y. Wang, S. Y. Zhang and Y. W. Du, J. Magn. Magn. Mater., 2000, 222, 110 CrossRef CAS.
- W. Zhong, W. Cheng, W. P. Ding, N. Zhang, Y. W. Du and Q. J. Yan, Solid State Commun., 1998, 106, 55 CrossRef CAS.
- A. Jerbi, R. Thaljaoui, A. Krichene and W. Boujelben, Phys. B, 2014, 442, 21–28 CrossRef CAS.
- Y. Regaieg, M. Koubaa, W. Cheikhrouhou Koubaa, A. Cheikhrouhou and T. Mhiri, J. Alloys Compd., 2010, 502, 270–274 CrossRef CAS.
- R. Thaljaoui, W. Boujelben, M. PeR kała, D. Pociecha, J. Szydłowska and A. Cheikhrouhou, J. Alloys Compd., 2012, 530, 138 CrossRef CAS.
- R. Skini, M. Khlifi, M. Triki, E. Dhahri and E. K. Hlil, J. Chem. Phys., (2015), 452, 67 Search PubMed.
- Y. Sun, X. Xu and Y. Zhang, J. Magn. Magn Mater., 2000, 219, 183 CrossRef CAS.
- L. Xu, J. Fan, Y. Zhu, Y. Shi, L. Zhang, L. Pi, Y. Zhang and D. Shi, Mater. Res. Bull., 2016, 73, 187 CrossRef CAS.
- F. Ayadi, W. Cheikhrouhou-Koubaa, M. Koubaa, S. Nowak, L. Sicard, S. Ammar and A. Cheikhrouhou, Mater. Chem. Phys., 2014, 145, 56 CrossRef CAS.
- N. Zaidi, S. Mnefgui, J. Dhahri and E. K. Hlil, RSC Adv., 2015, 5, 31901 RSC.
| This journal is © The Royal Society of Chemistry 2016 |






