Isochronal superposition and density scaling of the intermolecular dynamics in glass-forming liquids with varying hydrogen bonding propensity

Abstract

We have tested the idea of thermodynamic scaling T⁻¹ρ^γ and isochronal superposition in glass-forming liquids with varying propensity to form hydrogen bonds. The samples under investigation were dimeric rich ketoprofen and it is incapable of forming local hydrogen bonding structures, methylated derivative. We find that both features of viscous liquid dynamics hold better for the methylated sample and include the entire pressure-sensitive dynamics. We also show that it is possible to scale simultaneously the α- and secondary relaxation times in terms of T⁻¹ρ^−γ approach using the same value of the γ exponent. This is the first such clear observation reported for supercooled liquids to date. The removal of the hydrogen bonds enables these effects to be clearly identified experimentally.

---

A liquid is termed ‘supercooled’ if on lowering the temperature below the normal freezing (melting) point it bypasses crystallization and remains in a liquid state.¹ As believed, any liquid can avoid crystallization upon cooling if a sufficiently fast cooling rate is applied. For some liquids, this could be only 1 K min⁻¹, whereas for others (like metallic liquids) this is 10⁷ K s⁻¹. A supercooled liquid will eventually solidify upon lowering the temperature and form a glass (in which the molecular arrangement lacks the long-range order characteristic to crystalline materials). Typically, this happens around 80–140 K below the melting point.

The two most striking experimental findings regarding the dynamics of supercooled liquids are (i) isochronal superposition and (ii) density scaling. Based on high pressure dielectric relaxation studies, it has been established that for many glass-forming liquids the shape of the relaxation function depends only on the relaxation time and remains essentially the same in the whole T–p phase space. This property of glass-forming liquids is called isochronal superposition. In analogy to an isobar (or isotherm), which identifies (T, p) state points with the same pressure (or temperature), an isochrone signifies the curve in T–p space along which the relaxation process has exactly the same time scale. The results of numerous experimental studies have shown that the isochronal temperature–pressure superpositioning (TPS) of the α-relaxation is valid for liquids with van der Waals interactions, or any system lacking complex intermolecular bonding.^2–7 On the other hand, hydrogen bonding liquids generally violate isochronal superposition due to changes in the population of the HB structures induced by pressure (e.g. polyalcohols,⁸ glycols^9,10 or polyols¹¹). The other interesting feature of glass-forming liquids is related to the idea of scaling of dynamic quantities (such as structural relaxation time, viscosity or diffusion) with a single control variable, Γ = ρ^γ/T, where γ is the universal materials constant.^12–14 Scaling of the structural relaxation or viscosity when plotted versus ρ^γ/T was conformed for hundreds of materials, including van der Waals liquids and polymers, but not hydrogen bonding systems.^15,16 The scaling exponent γ is often linked to the intermolecular potential. For molecular liquids which interactions can be described purely in terms of the inverse power law (IPL) approximation, ∝r⁻ⁿ, the density scaling exponent γ = n/3 (ref. 17).

The experimental observation of the isochronal superposition and density scaling have followed development of the ‘isomorph theory’ that predicts for a special group of so-called ‘Roskilde-simple liquids’ the existence of isomorphic curves in the T–ρ phase diagram along which the structural, dynamic and some thermodynamic properties described using proper reduced units are invariant.^18,19 This special class of liquids is believed to include van der Waals bonded, metallic, weakly ionic liquids, but exclude most hydrogen-bonded or any other systems with strong directional bonding. The immediate criteria for a realistic liquid to fulfill the requirements of the simple Roskilde systems are density scaling and isochronal superposition.^20,21 Therefore, to a first approximation, the isomorphic curves examined only via molecular dynamics (MD) simulation can be related to the experimentally accessible isochrones.^22–24

By examining an increasing number of experimental results collected at varying thermodynamic conditions, it can be surprisingly concluded that in the conventionally available range of pressure (up to ∼0.5 GPa) the density scaling and isochronal superposition of the α-relaxation are satisfied to a large extent by an enormous number of glass-forming liquids with a diverse spectrum of intermolecular interactions, i.e. not only van der Waals liquids but also polymers, ionic liquids, and even strongly hydrogen bonding systems. For example, the isochronal superposition and T⁻¹ρ^γ scaling was reported for various ionic liquids, although their dynamic behavior in the supercooled regime is determined by a combination of hydrogen bonding, van der Waals and columbic interactions.^25,26 Similarly, a recent high-pressure dielectric relaxation study for glucose (an obviously strongly hydrogen bonded system) has demonstrated that the shape of the structural relaxation remains temperature and pressure invariant along isochrone.²⁷ It is also possible to scale individual Debye and structural relaxations in monohydroxy alcohols capable of forming HB supramolecular structures.²⁸ From the above, the isochronal superposition and density scaling emerge as more universal and intuitive features that cannot be limited to only glass-forming liquids lacking hydrogen bonding interactions or complex structural formation. It also contests whether both experimental observations (i) and (ii) are the sufficient experimental indicators of the simple Roskilde systems in the case of real liquids. The abovementioned issue stimulates in-depth examination of the isochronal superposition and density scaling concepts for molecular liquids with and without hydrogen bonding tendencies, particularly finding the accurate approach that would help evaluate their precision and the range of applicability.

Because of the rich diversity among glass-forming materials, a useful strategy to get relevant information on the dynamic properties of the viscous liquids and the role of intermolecular interactions is to tamper with the molecular structure to probe the exact effect of the specific chemical moiety on the behaviour of liquids in the vicinity of the glass-transition. The aim of this study is to test the idea of density scaling and isochronal superposition for a model low molecular weight hydrogen bonded liquid ketoprofen and its non-hydrogen bonding equivalent. The results of MD simulation have demonstrated that ketoprofen molecules form a significant number of hydrogen bonded cyclic and linear structures. On approaching the glass-transition, it is expected that the dynamic equilibrium between intermolecular HB cyclic and linear forms is shifted towards the former.²⁹

In this study, we have inhibited chemically the propensity to form HBs by replacing the hydroxyl group (–OH) by the methoxy unit –OCH₃ (see the chemical structures in Fig. 1). Consequently, the initial and final ketoprofen samples differ only in the tendency to form intermolecular hydrogen bonds. Therefore, they constitute ideal materials for a direct comparison of the dynamic features between typical van der Waals and hydrogen bonding glass-forming liquids. We have conducted dielectric relaxation measurements at elevated pressure using commercial high-pressure equipment from Unipress (Warsaw, Poland) and a Novocontrol Alpha analyser (Montabaur, Germany). Detailed analysis of the temperature and pressure dependences of structural relaxation time for the studied samples can be found elsewhere.^15,30 Pressure–volume–temperature (PVT) measurements were performed using a Gnomix dilatometer operating within the range of pressure from 0.1 to 200 MPa. For the studied samples, the supercooled liquid regime starts just below the melting point (T_m = 366.7 K for RS-ketoprofen, T_m = 324 K for Me-RS-ketoprofen³¹) and continues down to the glass transition temperatures.

Fig. 1 Chemical structures of (a) ketoprofen and (b) methyl ester of ketoprofen.

In the inset of Fig. 2, we show dielectric loss spectra for ketoprofen and its methyl ester with approximately the same position of the α-loss maxima. In both cases, the entire spectrum is composed of well-pronounced α-relaxation and secondary modes detected at higher frequencies. The former reflects cooperative reorientational dynamics related to the glass-transition, while the latter reflects more local non-cooperative processes (labelled in order of decreasing time scale by using the consecutive Greek letters β, γ). The removal of the hydrogen bonds lowers the glass transition temperature from 266.5 K for ketoprofen to 228.3 K for its methylated derivative.³¹ However, this has essentially no effect on the dispersion of the α-relaxation, as clearly demonstrated by the normalized spectra (main figure). We also note, it is not possible to superimpose secondary processes while maintaining constant τ_α.

Fig. 2 Comparison of the shape of the normalized dielectric loss spectra measured for RS-ketoprofen and Me-RS-ketoprofen at 0.1 MPa. The inset shows raw dielectric loss spectra before normalization. The arrows show the position of the primitive frequency as calculated from the coupling model (CM). For ketoprofen, the intermediate location of the primitive frequency ν₀ indicates that the well-separated secondary relaxation is not Johari–Goldstein (JG) type.

By applying the coupling model (CM), Sailaja and co-workers have identified this well-resolved secondary relaxation in ketoprofen (termed as γ-relaxation of activation energy, E_a = 37.91 kJ mol⁻¹ in the glassy state) as originating from the intramolecular motions.³² In this case, the primitive relaxation/true Johari–Goldstein (JG) β-relaxation is located on the high frequency side of the α-loss peak, which is too close to the main process to be detected as a separate relaxation. Using the CM equation (τ₀ = t_c^1−β_KWWτ_α^β_KWW,³³ with t_c = 2 ps and the fractional exponent of the Kohlrausch–Williams–Watts function β_KWW = 0.71 describing the breadth of the α-relaxation for methylated and non-methylated samples), we have estimated the position of the primitive relaxation (τ₀ ≈ τ_β), which is indicated by arrows in the inset of Fig. 2. Clearly in both cases, the expected JG β-relaxation/primitive relaxation of CM is located in the intermediate region between α- and γ-loss peaks, or, as termed in the literature, on an ‘excess wing’. For the methyl ketoprofen ester, the excess wing is probably more evident, as there is no faster γ-relaxation. Moreover, on approaching a glass transition, it transforms to a secondary process of the activation energy 47 ± 1 kJ mol⁻¹ in the glassy state. As there is no evident γ mode detected in the dielectric loss spectra of methylated ketoprofen, we presume that it might be somehow related with the presence/absence of the hydrogen bonds. A similar finding was reported by Grzybowska et al. for dipropylene glycol and its non-hydrogen bonding analogue.⁹

As resulted from the CM, the strong connection between α- and β-relaxations brings about the invariance of the τ_α − τ_β dependences and dispersion of the dielectric spectrum to different combinations of temperature and pressure while keeping τ_α constant.³⁴ In such a case, the isochronal superposition and the density scaling (with the same value of the scaling exponent) should apply to both types of movements. In this line, none of the secondary relaxations that has an intramolecular origin would scale, because at various thermodynamic conditions the dynamics is far too sluggish with respect to the density change. Similarly, in terms of the isomorph theory, it is predicted that for ‘simple-Roskilde’ systems the isochronal superposition holds only for intermolecular processes.⁶

By applying pressure, we have tested the idea of isochronal superposition for the studied samples. Fig. 3a and b show dielectric loss spectra obtained upon pressurization at fixed temperature for ketoprofen and its non-hydrogen bonding analogue, respectively. When the pressure is applied, the α-relaxation moves towards lower frequencies, in analogy to the same effect caused by decreasing the temperature at constant pressure. However, we have also noted that the behavior of the faster dynamics is completely different for both compounds. In the case of hydrogen bonded ketoprofen, the position of the secondary γ-relaxation remains practically unchanged, whereas for the methylated derivative the secondary process shifts upon applying pressure. This result indicates that the molecular movement responsible for the occurrence of γ-relaxation in ketoprofen almost does not sense changes in the density. On the other hand, for methylated ketoprofen, γ-relaxation was not detected in the loss spectra, possibly because individual molecules are no longer involved in the intermolecular hydrogen bonding. More importantly, the removal of the hydrogen bonds enables revelation of the secondary mode, which, similarly to the α-relaxation, is sensitive to pressure effects. For the methylated sample, the calculated value of the activation volume for the secondary relaxation detected upon isothermal measurements at 299 K is 32 ± 10 cm³ mol⁻¹, which is rather a significant number considering that for the cooperative α-relaxation at the same temperature ΔV = 136 ± 1 cm³ mol⁻¹. Large value of ΔV is a strong indication that this secondary process involves movement of either the whole molecule or a considerably large part of the molecule.

Fig. 3 Dielectric loss spectra for (a) RS-ketoprofen and (b) Me-RS-ketoprofen measured along isotherm T-308 K (from 70 MPa to 220 MPa) and T = 299 K (from 343 MPa to 443 MPa), respectively.

Using results from isobaric and isothermal dielectric relaxation studies, we have demonstrated in Fig. 4 the idea of isochronal superposition. Dielectric loss spectra collected at various combinations of temperature and pressure but with approximately the same position of α-loss peak frequency were normalized and plotted together, separately for ketoprofen in Fig. 4a and methyl ester of ketoprofen in Fig. 4b. Along the same isochrone, the shape of the α-relaxation remains temperature and pressure invariant, indicating that within the studied range of thermodynamic conditions the physical structure of dimer-rich ketoprofen is not modified by pressure to an extent that would affect the dispersion of α-relaxation. However, by inspecting the faster dynamics, we find that for the methylated derivative the isochronal superposition is more fulfilled and includes all pressure-sensitive dynamics composed not only from the α-relaxation but also the secondary modes of either inter or intramolecular origin. To date, this is the first such distinct observation that the temperature–pressure superpositioning might include the entire dielectric response of the supercooled liquid.

Fig. 4 Normalized dielectric loss spectra for (a) RS-ketoprofen and (b) Me-RS-ketoprofen taken at different (T, p) conditions but with approximately the same ν_max.

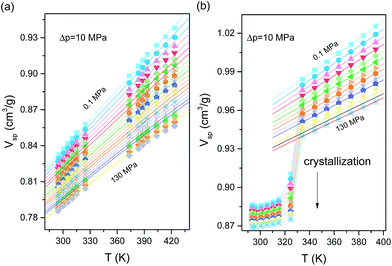
The next step in our investigations was to verify the density scaling idea of the relaxation dynamics for supercooled ketoprofen and its methylated analogue. This requires the temperature (T) and density (ρ) dependences of the relaxation time to be determined. In practice, to calculate the density at each (T, p) state point, pressure–volume–temperature (PVT) data are needed. In Fig. 5b, we have demonstrated the results of volumetric studies for RS-ketoprofen ad Me-RS-ketoprofen. Upon slow cooling (∼0.5 K min⁻¹) of ME-RS-ketoprofen crystallization was recorded as a sudden drop of the V_sp. It can be easily avoided, but this requires faster changes of the temperature during cooling, which are not of key importance during standard PVT measurements. The value of the specific volume in the supercooled liquid state depends on the current value of pressure, temperature and history of experimental observation. The time required for temperature and pressure stabilization is also needed. For Me-RS-ketoprofen, the crystallization process occurred abruptly, as the time required to form the crystalline phase was faster than the applied cooling rate. At the same time, no signs of crystallization were reported for RS-ketoprofen, which indicates that in the studied range of temperature and pressure it shows better glass-forming ability than its non-hydrogen bonded analogue. We will discuss this aspect elsewhere.

Fig. 5 Measured PVT data for (a) RS-ketoprofen and (b) Me-RS-ketoprofen. Specific volume as a function of temperature along isobars. Solid lines represent the best fits to the equation of state (EOS) equation for supercooled liquids.

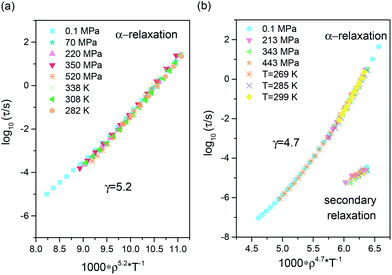
Description of the V_sp(T, p) dependence in the liquid state is typically carried out by means of equations of state, which allows satisfactory description of the dependence of the specific volume for a supercooled liquid in the temperature range in which the crystallization process might occur, or in any other situation in which the T–p range upon volumetric studies is limited because of the experimental difficulties.^15,35 We parametrized the PVT results with the use of the equation of state for supercooled liquids, V(T, p) = A₀ + A₁(T − T₀) + A₂(T − T₀)²/{[1 + (p − p₀)b₁ exp[b₂(T − T₀)]]^1/γ_EOS.^36,37 Then, the density scaling idea was tested for the investigated samples. The results of ρ^γ/T scaling are demonstrated in Fig. 6a and b. As can be observed, all isothermal and isobaric τ_α dependences overlap onto a master curve when plotted as a function of the scaling variable ρ^γ/T. Values of the γ exponents used to scale α-relaxation dynamics were obtained from fitting τ_α(T, V) dependences to the modified Avramov model.³⁸ The scaling exponents γ that obtain the best superpositioning of the α-relaxation dynamic are γ = 5.2 for ketoprofen and γ = 4.7 for methyl ketoprofen ester. For the latter, we surprisingly note that the density scaling with the same value of the exponent γ applies for both primary and secondary relaxations, as analysed above the glass transition temperature. This finding gives clear experimental evidence that the density scaling can be obeyed by the entire pressure-sensitive dynamics in the viscous liquid state. Previously, Ngai et al.³⁴ reported simultaneous ρ^γ/T (γ = 3.5) scaling of the α- and β-relaxation for DGEBA (diglycidyl ether of bisphenol A). However, the secondary β-relaxation times were taken from the glassy states, and the density data determined below the glass transition rests on extrapolation of the values of glass compressibility and expansivity. Therefore, we report here for the first time the validity of the density scaling for secondary dynamics tested directly in the supercooled liquid state.

Fig. 6 Alpha-relaxation times plotted as a function of 1000 × ρ^γ × T⁻¹ product for (a) RS-ketoprofen with γ = 5.2 and (b) Me-RS-ketoprofen with γ = 4.7. Density data were taken from PVT data. Scaling exponents were obtained from fitting of the τ_α(T, V) dependences to the modified Avramov equation.

By visually comparing the obtained results, it is also evident that the ρ^γ/T scaling relation for α-relaxation times is conformed to better precision by the methylated derivative. In addition, it holds for the secondary mode, which, similar to the α-relaxation, recognizes changes in the molecular packing. This process is possibly also present in the supercooled liquid state of ketoprofen, but due to the intensity of the γ-relaxation, we are not able to detect it. Nevertheless, for ketoprofen, it is still possible to provide a good description of the structural relaxation data in terms of the density scaling, especially keeping in mind its strong tendency to form HB dimers. Because the experimentally determined values of the γ exponent provide an insight into the microscopic interactions between molecules, we can conjecture that these should be a bit different for ketoprofen and its methylated derivative. In addition, it is interesting to point out that this study shows that the same information about the intermolecular potential as that embedded in the scaling exponent γ can be provided by both, structural and more local (non-cooperative) secondary processes of the different molecular nature.

A justification that the scaling exponent γ provides an insight into the intermolecular interactions can be given by referring to liquids with simple Lennard-Jones-like interactions for which the intermolecular potential energy can be approximated by the interparticle repulsive forces (∝r⁻ⁿ, where r is the distance between particles) with a weak attractive term acting only as a uniform background.³⁹ For the inverse power law (IPL) for liquids, it was demonstrated that the density scaling is rigorously obeyed with γ = n/3.^40–42 Therefore, for a simple system interacting perfectly via LJ 6–12 potential (repulsive term ∼r⁻¹² and attractive term ∼r⁻⁶) the scaling behaviour is obtained with exponent γ = 4 (as the repulsive part ∝r^−3γ).

By taking into account the dynamic properties of supercooled ketoprofen, it is also obvious that it does not hold characteristic hallmarks of other hydrogen-bonded liquids capable of forming extensive HB networks. The presence of dimeric hydrogen bonded structures is not able to affect the isochronal superposition or the density scaling, whereas it becomes rather well-established that these features of glassy dynamics are commonly violated for the hydrogen bonding systems. Therefore, the present study gives new evidence that the dynamic behaviour of the entire group of the ‘HB systems’ is more diverse than their most representative examples. The relaxation dynamics of supercooled ketoprofen inherit unconsciously much from the properties of its van der Waals liquids counterpart. However, one of the things that distinguish both supercooled liquids is the behaviour of more local dynamics that disclose different pressure sensitivity depending on the propensity to form intermolecular hydrogen bonds.

To sum up, this study has focused on testing the validity of isochronal superposition and density scaling for two molecular liquids differing only in the propensity to form hydrogen bonded dimeric structures. We show that both features of viscous liquid dynamics can be obeyed irrespectively of the tendency to form intermolecular hydrogen bonds. This is in contrast to some previous results reported for strongly associated liquids. However, it is evident that the isochronal superposition and the density scaling hold better for the non-hydrogen bonding sample and include not only the structural relaxation but also local pressure sensitive dynamics. Thus, the results given in this study should urge investigators to look for a more precise approach that would help evaluate and rank the accuracy of the isochronal superposition and density scaling for various glass-forming systems, especially if both criteria are used to distinguish the real glass-forming liquids to be ‘simple Roskilde’ or not. Finally, scaling of the secondary relaxation times in terms of the ρ^γ/T law with the same value of the γ exponent as that necessary to superimpose structural relaxation times might indicate that from the non-cooperative local dynamics it is possible to obtain the same information about the intermolecular forces as that provided from the cooperative α-relaxation mode. However, this hypothesis should be tested in more detail theoretically.

Acknowledgements

K. A. and M. P. are grateful for the financial support from the National Science Centre within the framework of the OPUS project (Grant No. DEC 2014/15/B/ST3/00364).

Notes and references

1. D. Turnbull, Contemp. Phys., 1969, 10, 473–488.
2. C. M. Roland, R. Casalini and M. Paluch, Chem. Phys. Lett., 2003, 367, 259.
3. K. L. Ngai, R. Casalini, S. Capaccioli, M. Paluch and C. M. Roland, J. Phys. Chem. B, 2005, 109, 17356.
4. S. Hensel-Bielowka, S. Pawlus, C. M. Roland, J. Ziolo and M. Paluch, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 050501(R).
5. S. Pawlus, M. Paluch, M. Sekula, K. L. Ngai, S. J. Rzoska and J. Ziolo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 021503.
6. L. A. Roed, D. Gundermann, J. C. Dyre and K. Niss, J. Chem. Phys., 2013, 139, 101101.
7. K. L. Ngai, Relaxation and Diffusion in Complex Systems, Springer, Heidelberg, 2011.
8. S. Pawlus, M. Paluch, M. Nagaraj and J. K. Vij, J. Chem. Phys., 2011, 135, 084507.
9. K. Grzybowska, S. Pawlus, M. Mierzwa, M. Paluch and K. L. Ngai, J. Chem. Phys., 2006, 125, 144507.
10. R. Casalini and C. M. Roland, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 094202.
11. S. Pawlus, M. Paluch, J. Ziolo and C. M. Roland, J. Phys.: Condens. Matter, 2009, 21, 332101.
12. A. Tölle, Rep. Prog. Phys., 2001, 64, 1473.
13. C. Alba-Simionesco, D. Kivelson and G. Tarjus, J. Chem. Phys., 2002, 116, 5033.
14. G. Dreyfus, A. Le Grand, J. Gapinski, W. Steffen and A. Patkowski, Eur. J. Phys., 2004, 42, 309.
15. C. M. Roland, S. Hensel-Bielowka, M. Paluch and R. Casalini, Rep. Prog. Phys., 2005, 68, 1405–1478.
16. C. M. Roland, R. Casalini, R. Bergman and J. Mattsson, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 012201.
17. W. G. Hoover, S. G. Gray and K. W. Johnson, J. Chem. Phys., 1971, 55, 1128.
18. U. R. Pedersen, N. P. Bailey, T. B. Schrøder and J. C. Dyre, Phys. Rev. Lett., 2008, 100, 015701.
19. N. Gnan, C. Maggi, T. B. Schrøder and J. C. Dyre, Phys. Rev. Lett., 2010, 104, 125902.
20. D. Gundermann, U. R. Pedersen, T. Hecksher, N. P. Bailey, B. Jakobsen, T. Christensen, N. B. Olsen, T. B. Schrøder, D. Fragiadakis, R. Casalini, C. M. Roland, J. C. Dyre and K. Niss, Nat. Mater., 2011, 7, 816–821.
21. W. Xiao, J. Tofteskov, T. V. Christensen, J. C. Dyre and K. Niss, J. Non-Cryst. Solids, 2015, 407, 190–195.
22. N. Gnan, T. B. Schrøder, U. R. Pedersen, N. P. Bailey and J. C. Dyre, J. Chem. Phys., 2009, 131, 234504.
23. L. Bøhling, N. P. Bailey, T. B. Schrøder and J. C. Dyre, J. Chem. Phys., 2014, 140, 124510.
24. U. R. Pedersen, N. Gnan, N. P. Bailey, T. B. Schrøder and J. C. Dyre, J. Non-Cryst. Solids, 2011, 357, 320–328.
25. M. Paluch, Z. Wojnarowska, P. Goodrich, J. Jacquemin, J. Pionteck and S. Hensel-Bielowka, Soft Matter, 2015, 11, 6520.
26. G. Jarosz, M. Mierzwa, J. Ziolo, M. Paluch, H. Shirota and K. L. Ngai, J. Phys. Chem. B, 2011, 115, 12709–12716.
27. E. Kaminska, M. Tarnacka, K. Jurkiewicz, K. Kaminski and M. Paluch, J. Chem. Phys., 2016, 144, 054503.
28. A. Reiser, G. Kasper, C. Gainaru and R. Böhmer, J. Chem. Phys., 2010, 132, 181101.
29. M. T. Ottou Abe, N. T. Correi, L.-C. Valdes, J. M. B. Ndjaka and F. Affouard, J. Mol. Liq., 2015, 205, 74–77.
30. K. Adrjanowicz, K. Kaminski, M. Paluch and K. Niss, Cryst. Growth Des., 2015, 15, 3257.
31. K. Adrjanowicz, K. Kaminski, M. Tarnacka, K. Szutkowski, L. Popenda, G. Bartkowiak and M. Paluch, Phys. Chem. Chem. Phys., 2016, 18, 10585–10593.
32. U. Sailaja, M. Shahin Thayyil, N. S. Krishna Kumar and G. Govindaraj, Eur. J. Pharm. Sci., 2013, 49, 333.
33. K. L. Ngai, J. Chem. Phys., 1998, 109, 6982–6994.
34. K. L. Ngai, J. Habasaki, D. Prevosto, S. Capaccioli and M. Paluch, J. Chem. Phys., 2012, 137, 034511.
35. G. Floudas, M. Paluch, A. Grzybowski and K. L. Ngai, Molecular Dynamics of Glass-Forming Systems – Effect of Pressure, Springer-Verlag, 2011.
36. A. Grzybowski, K. Grzybowska, M. Paluch, A. Swiety and K. Koperwas, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 041505.
37. For RS-ketoprofen: T₀ = 273 K, P₀ = 0.1 MPa, A₀ = 0.81692 cm³ g⁻¹, A₁ = 7.70996 × 10⁻⁴ cm³ (g K)⁻¹, A₂ = 3.40939 × 10⁻⁷ cm³ (g K²)⁻¹, BT₀(P₀) = 2801.353 MPa, b₂= 0.0052 K⁻¹, γ_EOS = 11.50016, log₁₀(τ₀/s) = −9.79695, A = 207.27722 cm^3γ g^−γ K, D = 2.92411, γ = 5.26105. For methyl ester of RS-ketoprofen: T₀ = 273 K, P₀ = 0.1 MPa, A₀ = 0.94481 cm³ g⁻¹, A₁ = 6.22509 × 10⁻⁴ cm³ (g K)⁻¹, A₂ = 3.66938 × 10⁻⁷ cm³ (g K²)⁻¹, BT₀(P₀) = 2925.28003 MPa, b₂= 0.00539 K⁻¹, γ_EOS = 11.93974, log₁₀(τ₀/s) = −10.60884, A = 310.99349 cm^3γ g^−γ K, D = 3.52145, γ = 4.76756.
38. R. Casalini, U. Mohanty and C. M. Roland, J. Chem. Phys., 2006, 125, 014505.
39. D. Chandler, J. D. Weeks and H. C. Andersen, Science, 1983, 220, 787–794.
40. Y. Hiwatari, M. Matsuda, T. Ogawa, N. Ogita and A. Ueda, Prog. Theor. Phys., 1974, 52, 1105.
41. W. G. Hoover and M. Ross, Contemp. Phys., 1971, 12, 339.
42. L. Bøhling, T. S. Ingebrigtsen, A. Grzybowski, M. Paluch, J. C. Dyre and T. B. Schrøder, New J. Phys., 2012, 14, 113035.

---