Geometric, magnetic and electronic properties of folded graphene nanoribbons

Abstract

Geometric, magnetic and electronic properties of folded graphene nanoribbons (GNRs) are investigated by first-principles calculations. These properties are mainly dominated by the competition or cooperation among stacking, curvature and edge effects. For the folded zigzag GNRs, the more stable structures are revealed to be AB stackings, while for the armchair types, AA′ stackings are more stable. The interlayer interactions and hybridization of four orbitals lead to smaller energy gaps, anti-crossing bands, and more band-edge states. Specifically, the edge atoms, with the different magnetic environments, in the odd-zAB-stacked folded zigzag GNRs are responsible for the spin-up and spin-down splitting subbands. All folded GNRs are direct-gap semiconductors except that the edge–edge interactions cause the even-zAA-stacked folded zigzag GNRs to exhibit a pair of metallic linear bands. The width-dependent energy gaps in the folded armchair GNRs can be classified into six categories. Furthermore, there exist rich features in density of states, including the form, number, intensity and energy of the special structures.

---

1 Introduction

In 2004, graphene was first successfully synthesized,¹ and since then has attracted considerable attention in the fields of chemistry, materials science and physics.^2–8 The unique two-dimensional (2D) hexagonal symmetry induces rich electronic properties, such as an extremely high mobility,² an anomalous quantum Hall effect,^2,6 and ambipolar transport phenomena.¹ Graphene is viewed as a future electronic materials. However, its zero-gap property makes actual applications in logic electronics difficult. In order to further expand the range of applications, opening an energy gap is critical. Semiconducting 1D nanoribbons (GNRs) have been the focus of many experimental^9–22 and theoretical studies.^23–39 GNRs have been successfully produced from graphene through lithographic techniques^9,10 and from carbon nanotubes by several chemical and physical unzipping methods.^11–13 Under different growing environments, GNRs with various structures are presented in laboratories, including few-layer,¹³ curved,¹⁴ scrolled,¹⁵ and folded types.^16–20 The unique stacking configuration and curved structure in folded GNRs are worth detailed studies.

Flat GNRs possess rich geometric and electronic properties, being dominated by their edge structures and ribbon widths. The typical zigzag and armchair GNRs have the achiral boundaries. A zigzag GNR (ZGNR) is a middle-gap semiconductor with two edge-state electrons, which have a ferromagnetic arrangement for each edge but an antiferromagnetic one across the nanoribbon.²³ The zigzag systems are considered as potential materials for future applications in spintronic devices, mainly owing to their halfmetallic characteristics under a transverse electric field.²⁷ On the other hand, all armchair GNRs (AGNRs) are direct-gap semiconductors, which can be classified into three categories of energy gaps, being mainly determined by the number of dimer lines (N_a). The largest (smallest) energy gaps are reported to be at N_a = 3n + 1 (N_a = 3n + 2); n is a positive integer. All energy gaps are inversely proportional to the ribbon width for each category.²³

In previous research studies, the fundamental properties of GNRs with various curvatures or stackings have not been thoroughly explored. Few-layer GNRs²⁸ present various stacking configurations. The atomic interactions between two layers strongly depend on the van der Waals interactions. The edge–edge interactions^28,29 are introduced by the open edges in some specific configurations. Hence, the electronic properties are dominated by both the stacking- and the edge-related interactions. The hybridization of four orbitals (2s, 2p_x, 2p_y, 2p_z) in curved ribbons^24,36 and nanoscrolls causes the complex bondings at the inner side of the curved surface. The larger 2p_z orbitals on the outer side of the curved surface provide a compatible environment for adsorbed atoms, such as H and Li.^30,31 As a result, curved systems are promising materials for future hydrogen storage or lithium batteries. Due to the cooperation or competition among the stacking, curvature, and edge effects, a folded GNR with curved and stacking parts (Fig. 1) is expected to display intricate and versatile electronic properties. In experiments,^16–20 the synthesized folded GNRs have displayed distinct physical characteristics. Experimental measurements from scanning tunneling microcopy show that folded GNRs can be formed in various stacking configurations.^17,18 On the theoretical side, there are some reports on the essential properties of the folded GNRs.^34–39 The quantum Hall effects are investigated using the tight-binding model.^34–36 The first-principles calculations are used to evaluate the folding energy, optimal geometry and band structure of the folded AGNRs.^36–38 However, stacking effect and width dependence are not taken into account. The similar properties are also studied for the folded ZGNRs,³⁸ but the spin polarization is not included in the calculations. The electronic structure in the presence of spin configuration and electric field is calculated by the general gradient approximation (GGA) without the critical van der Waals interactions.³⁹ The above-mentioned reports are mainly focused on the AA stacking configuration, but few investigations have been carried out for the more stable AB ones and other potential configurations.^17,18 Apparently, knowledge of the folding energy, band structure, density of states (DOS), and band gap (E_g), geometric structure, and magnetism for various stacking configurations has not been explored thoroughly.

Fig. 1 (a)–(c) are structure of a flat ZGNR with N_z of zigzag chains, and of the folded ZGNR, side view of the folded ZGNRs, respectively. (d)–(f) represent, separately, structure of a flat AGNR with N_a of dimer chains, and of the folded AGNR, side view of the folded AGNRs. (g) The AA, AB, AA′ stacking manner for bilayer graphene.

In this paper, the geometric, magnetic and electronic properties of folded GNRs with various widths are investigated in detail by the first-principles calculations. The high-symmetry stacking configurations, AA, AB and AA′, are also taken into account. Among the complex structures, we systematically classify four types of zigzag and armchair systems, based on the edge structure, folding energy, ribbon width and stacking configuration. The armchair systems are further divided into six categories of width-dependent energy gaps on the basis of the stacking configurations. Each of these eight types of folded GNRs presents distinct electronic properties, such as a pair of metallic linear bands, the metal–semiconductor transitions, the splitting of spin-up and spin-down states, and the monotonous width dependence of the energy gap. Moreover, the predicted main features in DOS are validated and compared to experimental scanning tunneling spectroscopy (STS) measurements. These rich fundamental features in folded GNRs can be expected to provide potential applications in energy materials, as well as electronic and spintronic devices.

2 Computational details and structural properties

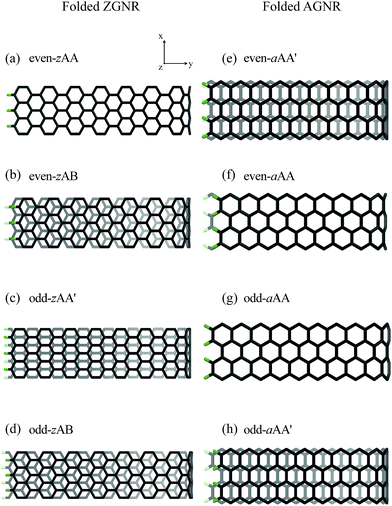
We use the Vienna ab initio simulation package^40,41 in the density-functional theory (DFT) to investigate the essential properties of folded GNRs. The DFT-D2 method⁴² is taken into account in order to describe the weak van der Waals interactions. The electron–ion interactions are obtained by the projector-augmented wave method, and the exchange and correlation electron–electron interactions are calculated from the generalized gradient approximation⁴³ with Perdew–Burke–Ernzerhof. The wave functions are expanded by the plane waves with a maximum kinetic energy of 500 eV. For electronic properties and optimized geometric structures, the first Brillouin zone is, respectively, sampled by 300 × 1 × 1 and 12 × 1 × 1 k-points in the Monkhorst–Pack scheme. All of the atoms are relaxed until the Hellmann–Feynman force is less than 0.03 eV Å⁻¹. A vacuum space of 15 Å is inserted between periodic images to simulate an isolated folded GNR.

Geometric structures of the folded GNRs are diversified by the stacking, edge structure and width. The width of a flat ZGNR (AGNR) is characterized by the number of zigzag (dimer) lines along the transverse y-axis, as shown in Fig. 1(a) and (d). By folding a single flat GNR, a folded GNR can be viewed as two flat ribbons connected by a fractional nanotube in the position to create the curved surface (Fig. 1(b) and (e)). The open edges are passivated by hydrogen atoms (green balls). There are three high-symmetry stacking configurations between two flat ribbons, including AA, AB and AA′ ones (Fig. 1(g)). Specially, the AA′ stacking is an intermediate configuration between AA and AB ones, where the C–C dimer of the upper (lower) layer is projected at the hexagon center of the lower (upper) layer. According to the number of zigzag and armchair lines, ZGNRs and AGNRs, respectively, possess four types of stable geometric structures, including an even N_z with AA (even-zAA) and AB (even-zAB) stackings (Fig. 2(a) and (b)), an odd N_z with AA′ (odd-zAA′) and AB (odd-zAB) ones (Fig. 2(c) and (d)), an even N_a with AA′ (even-aAA′) and AA (even-aAA) ones (Fig. 2(e) and (f)); an odd N_a with AA (odd-aAA) and AA′ (odd-aAA′) ones (Fig. 2(g) and (h)). For the even-zAA (Fig. 2(a)), odd-zAA′ (Fig. 2(c)), even-aAA′ (Fig. 2(e)) and odd-aAA stackings (Fig. 2(g)), the edge of the upper layer lines up with that of the lower layer; that is, all the edge atoms have the same y positions. The even-zAA (Fig. 2(a)) and odd-aAA stackings (Fig. 2(g)) have the mirror symmetry about the x–y plane, while the odd-zAA′ (Fig. 2(c)) and even-aAA′ ones (Fig. 2(e)) have the C₂ rotation symmetry about the y-axis. Specially, the even-zAB and odd-zAB stackings can be, respectively, realized by shifting the upper layers of the even-zAA and odd-zAA′ stackings with the distances of b and b/2 (b is the C–C bond length). Also, a similar relation exists between the even-aAA and even-aAA′ stackings (the odd-aAA′ and odd-AA ones), but by shifting a distance of .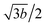

Fig. 2 Top views of folded ZGNRs with respect to (a) even-zAA, (b) even-zAB, (c) odd-zAA′, and (d) odd-zAB. Top views of folded AGNRs with respect to (e) even-aAA′, (f) even-aAA, (g) odd-aAA, and (h) odd-aAA′. The light (dark) gray balls denote the upper (lower) layer carbon atoms of GNRs, and the pink balls are the terminated H atoms.

3 Optimal geometry and folding energy

Each stacking configuration exhibits unique geometric properties. The curved and flat parts of a folded GNR, separately, determine the nanotube diameter (D_c) and the interlayer distance (D_f) (Fig. 1(c) and (f)). The former represents the influence of the ribbon curvature, and the latter reflects the stacking effect. Both distances are significantly affected by the ribbon width and stacking configuration. Nanotube diameter, interlayer distance and folding energy present the unusual width- and configuration-dependence. For folded ZGNRs, the width-dependent behavior of D_c and D_f is similar for the four types of stacking configurations, as shown in Fig. 3(a). D_c initially grows with an increase of N_z and then reaches a saturated value at N_z ≥ 40. For large N_z's, D_c's of the even-zAA, even-zAB, odd-zAA′ and odd-zAB stackings are, respectively, 9.2 Å, 9.3 Å, 8.7 Å and 8.5 Å. Moreover, D_f's are less affected by N_z. This weak dependence is reflected in the saturated D_f's which are, respectively, 3.5 Å, 3.2 Å, 3.3 Å and 3.2 Å at N_z ≥ 38 following the same sequence as for D_c's. For armchair systems (Fig. 3(b)), on the other hand, the N_a-dependence of D_c is different from the above-mentioned relations. D_c weakly depends on the ribbon width except for the even-aAA stacking, whose D_c decreases with increasing N_a and then reaches a final value at N_a ≥ 40. D_c's of the even-aAA, even-aAA′, odd-aAA, and odd-aAA′ stackings are, respectively, 7.1 Å, 7.0 Å, 7.0 Å, and 7.2 Å. The dependence of D_f on the ribbon width is negligible, and the D_f of the AA-stacked configuration is larger than that of the AA′-stacked one, regardless of the even or odd width. The perceivable D_f's of the AA and AA′ stackings are 3.5 Å and 3.3 Å, respectively.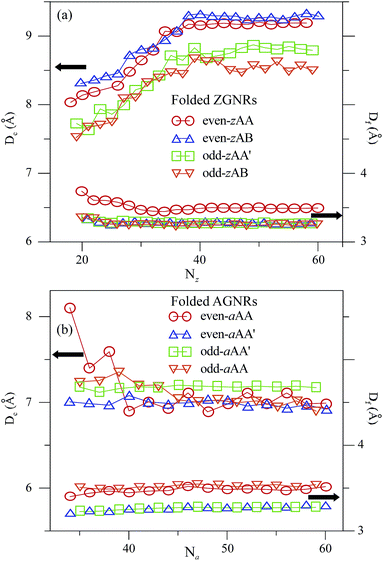

Fig. 3 Width-dependent D_c and D_f for different (a) folded ZGNRs and (b) folded AGNRs. The curves of the eight stacking configurations are as denoted.

When the ribbon width is large enough, both D_f and D_c are nearly constant. D_f is dominated by the stacking effect, meaning that even- and odd-zAB stackings have shorter interlayer distances. This result is in good agreement with those presented in bilayer graphene nanoribbons²⁸ and bilayer graphenes.⁴⁴ On the other hand, D_c is shorter in folded AGNRs compared with folded ZGNRs, indicating that the former are subjected to a larger deformation, or the latter are stiffer. This is consistent with the mechanical-strain response of the deformed flat GNRs⁴⁵ and carbon nanotubes.⁴⁶

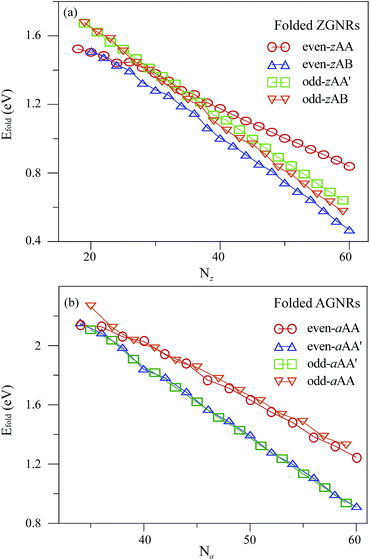
The folding energy (E_fold) is defined as the difference between the total energy of a folded GNR and that of a flat GNR. This energy is dominated by the interlayer interaction (E_stacked), the edge-induced energy (E_ee) and the bending energy (E_bend), which are mainly contributed by the flat two-layer interaction, the edge–edge interaction and the mechanical strain, respectively. E_stacked depends on D_f, the stacked manner and the length of the flat region; its magnitude increases as the length of this region but reduces as D_f grows. Moreover, the magnitude of E_ee increases as the distance between two edges (d_edge) decreases. E_bend is always larger than the sum of E_stacked and E_ee, so E_fold is greater than zero. E_fold decreases with the increasing width, because the edge–edge interaction and the bending energy for a saturated D_c are nearly unchanged, while the overlap area of two flat sheets grows in a widened ribbon. When the width is sufficiently wide (N_z ≥ 38 in Fig. 4(a)), E_fold's of zigzag systems exhibit the following descending order: even-zAA stacking > odd-zAA′ stacking > odd-zAB stacking > even-zAB stacking. The AB-stacked folded GNRs have a higher stability since they possess larger interlayer interactions. Moreover, the even-zAB stacking has a lower E_fold than the odd-zAB one. The d_edge's of both systems are, respectively, 3.1 Å and 3.6 Å, which leads to the stronger edge–edge interaction in the even stacking systems. Such influence is also applied to narrow ribbons; therefore, E_fold associated with the even-zAA stackings (d_edge = 2.9 Å) is lower than that of the odd-zAA′ ones (d_edge = 3.5 Å). On the other hand, the edge–edge interactions do not play an important role in the N_a-dependence of E_fold, but the relationship is dominated by the stacking configurations; AA′-stacked folded AGNRs are more stable than AA-stacked ones, irrespective of the dimer line number being even or odd (Fig. 4(b)). The edge–edge interaction is indistinguishable for the four types of folded AGNRs with almost the same d_edge (∼3.6 Å). When the ribbon width is larger, the reason for the folded AGNRs but not the folded ZGNRs having a higher E_fold can be explained by the fact that D_c is shorter in the former than in the latter.

Fig. 4 Width-dependent folding energies for various (a) folded ZGNRs, and (b) folded AGNRs.

4 Magnetic moments and electronic properties

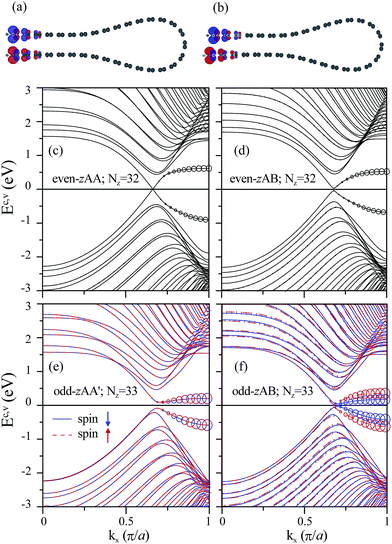
For the magnetism of GNRs, AGNRs prefer the nonmagnetic state, while ZGNRs favor the antiferromagnetic (ferromagnetic) arrangement for the two opposite edges (the same edge). Folded AGNRs remain non-magnetic; however, folded ZGNRs exhibit unique magnetic phenomena: the spin arrangements can be modified by the geometric structure. The folded ZGNRs with even N_z have no magnetic moments; nevertheless, the ones with odd N_z, like monolayer GNR,²³ present antiferromagnetic at the open edges. Each carbon atom in zigzag edge has the magnetic moment of 0.14 μ_B. The spin charge densities of odd-zAA and odd-zAB stackings are illustrated in Fig. 5(a) and (b), respectively. The magnetism of folded ZGNRs, as well as bilayer ZGNRs,²⁸ is dependent on the edge–edge interactions; that is, the strong interactions can effectively suppress the magnetic moments at a sufficiently short distance (d_edge < 3.5 Å). That d_edge's of the even-zAA, even-zAB, odd-zAA′ and odd-zAB stackings are 2.9, 3.1, 3.5, and 3.6 Å, respectively, accounts for the existence of magnetic moments. The magnetic moments affect the electronic properties significantly. The nonmagnetic systems predictably have different electronic structures in comparison with monolayer GNR. Moreover, the electronic properties of the magnetic systems can be modulated by the geometric structure.

Fig. 5 Partial charge densities with spin arrangements of (a) the odd-zAA′ and (b) odd-zAB of folded ZGNR. The red color indicates spin up and the blue color denotes spin down. Band structures of folded ZGNRs: (c) even-zAA, (d) even-zAB, (e) odd-zAA′; (f) odd-zAB configurations.

The various 1D folded GNRs present the feature-rich electronic properties. The band structures are significantly affected by the edge structure, stacking configuration, magnetism, curvature effect and ribbon width. The folded ZGNRs exhibit many 1D energy bands, as shown in Fig. 5(c)–(f). The occupied (E^v) and unoccupied (E^c) energy bands are asymmetric to the Fermi level (E_F = 0). Most of the subbands have parabolic energy dispersions. Each subband owns several band-edge states characterized by the local minima or maxima. These states are located at Brillouin zone center (k_x = 0) and boundary (k_x = π/a), and some are located in between them. At the higher-energy region, there are many anti-crossing subbands with band-edge states close to k_x = 1, mainly owing to the interlayer interactions and the enhanced hybridization of the four orbitals (2s, 2p_x, 2p_y, 2p_z) on the curved surface. In the low-lying subbands, the pair of subbands nearest to E_F in the regions of 2/3 ≤ k_x ≤ 1 and 0 ≤ k_x ≤ 2/3, respectively, possess the partially flat and parabolic dispersions. The former are mainly contributed by the local edge atoms (the circle radii representing the contributions of the edge atoms). These two subbands are quite different among the four types of folded ZGNRs. The even-zAA stackings belong to a 1D metal, while the other three systems are direct-gap semiconductors. The valence and conduction bands in the first systems intersect each other at E_F = 0, and the Fermi-momentum state is similar to the Dirac point in an armchair carbon nanotube.⁴⁷ The band crossing is also revealed in the AA-stacked bilayer graphenes,⁴⁸ bilayer ZGRNs,²⁸ and collapsed carbon nanotubes^49,50 because of the mirror symmetry in the AA stacking configuration. For the even-zAB stackings, the linearly intersecting bands become two anti-crossing parabolic bands with a narrow direct band gap (E_g), as shown in Fig. 5(d). The metal–semiconductor transition is caused by the destruction of mirror symmetry during the variation of stacking configuration, as observed in bilayer ZGNRs²⁸ and collapsed carbon nanotubes.⁴⁹ The non-magnetic even-zAA and even-zAB stackings are, respectively, metals and semiconductors. On the other hand, the antiferromagnetic odd-zAA′ and odd-zAB stackings are semiconductors with the spin-dependent band structures (Fig. 5(e) and (f)). The spin-up and spin-down subbands are doubly degenerate for the former, while the spin degeneracy is absent in the latter. The odd-zAB systems do not have the same y-coordinates for the edge atoms on the upper and lower layers (Fig. 2(d)), so that the magnetic environments are different for the spin-up and spin-down configurations (Fig. 5(b)). However, the odd-zAA′ stackings exhibit the opposite behavior (Fig. 2(c) and 5(a)). This is responsible for the spin splitting or degeneracy of the energy subbands. Among the semiconducting folded ZGNRs, the odd-zAA′ ones with various ribbons have the largest band gaps. In addition, the energy difference at zone boundary of folded ZGNRs with odd N_z is smaller than that with even N_z.

For the semiconducting folded ZGNRs, the band gaps strongly depend on the stacking configurations, edge–edge interactions and ribbon widths. E_g's monotonously decline with an increasing ribbon width, while those of the even-zAB stacking are insensitive to N_z (∼60 meV in Fig. 6). The difference in N_z-dependence is because the earlier explanation mechanism on the formation of energy gap in the even-zAB stacking considerably differs from what accounts for the odd-zAA′ and odd-zAB ones. E_g's of narrow folded ZGNRs exhibit the following descending order: odd-zAA′ stacking > odd-zAB stacking with spin down > odd-zAB stacking with spin up > even-zAB stacking. But when the ribbons are sufficiently wide (N_z ≥ 34), E_g's of the even-zAB stacking become larger than those of the odd-zAB ones.

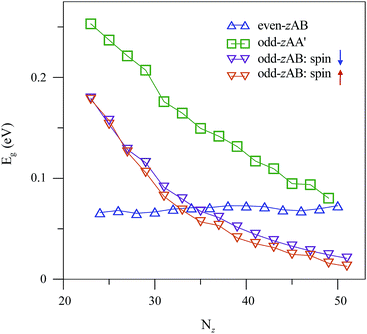Fig. 6 Width-dependent band gaps of folded ZGNRs. N_z is the number of zigzag chains in the folded ZGNRs and it relates to the width of the ribbon.

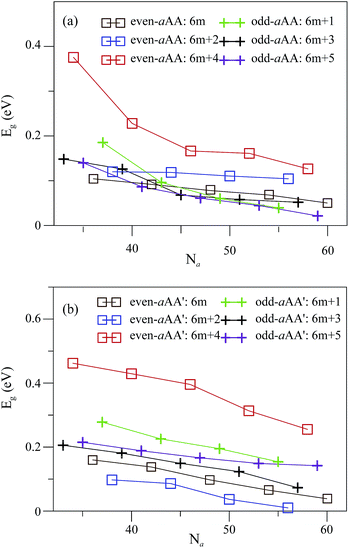
Compared to the band structures of folded ZGNRs, the folded AGNRs display an entirely different type of band structure (as depicted in Fig. 7). The edge bands are not found in the band structure of folded AGNRs. The folded AGNRs still preserve the band characters of the AGNRs. The top of valence band (TVB) and bottom of conduction band (BCB) of an folded AGNR are both located at Γ point (k_x = 0), whereas the TBV and BCB of a folded ZGNR are in the edge bands near the Brillouin zone boundary. The folded AGNRs are all direct band-gap semiconductors, while the ZGNR ones behave as semiconductors or semimetals. Their energy dispersions are almost independent of the stacking configuration, as shown in Fig. 7(a)–(h). In the low energy region of |E^c,v| ≤ 1 eV, each subband exhibits one band-edge state at k_x = 0. However, some of the band-edge states are doubly degenerate due to the stacking effect. All the folded AGNRs belong to direct-gap semiconductors, being determined by the k_x = 0 states. The energy gaps are sensitive to changes in the ribbon width and the stacking configuration. An oscillation of band gap with N_a is also found in folded AGNRs, however, a period of six N_a in E_g of folded ones is instead of three N_a that was discovered in flat AGNRs; similar oscillation also can be seen in the paper of Le and Woods,³⁷ the band-gap oscillation will be shown in Fig. 8 and discussed in next paragraph. The N_a = 34 even-aAA and N_a = 37 odd-aAA stackings possess larger energy gaps. Similar results have been predicted for the flat nanoribbon case, where the largest energy gap is from the category of N_a = 3m + 1, being attributed to the finite-width quantum confinement.²³ When the stacking configuration changes, the N_a = 34 even-aAA′ and N_a = 37 odd-aAA′′ systems also own larger energy gaps. In addition, the AA′ stacking has larger gaps than those possessed by the AA stacking.

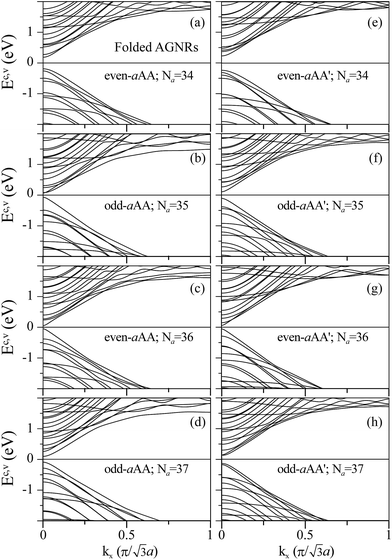Fig. 7 Band structures of AA stacked folded AGNRs: (a) N_a = 34, (b) N_a = 35, (c) N_a = 36; (d) N_a = 37. Band structures of AA′ stacked fold AGNRs: (e) N_a = 34, (f) N_a = 35, (g) N_a = 36; (h) N_a = 37.

Fig. 8 Width-dependent band gaps of folded AGNR with (a) AA, and (b) AA′ stacking.

The E_g of the flat and folded AGNRs oscillates with N_a but has different oscillating period, that is 3 N_a and 6 N_a for flat and folded AGNRs, respectively. E_g's of flat AGNRs are classified into three categories: 3n, 3n + 1 and 3n + 2, where the second (third) one has the largest (smallest) band gap. Similarly, the band gaps of folded AGNRs can be further divided into six categories, based on the two types of stacking configurations. E_g's corresponding to the AA and AA′ stackings, respectively, possess three N_a-relationships, all of which decline with a larger ribbon width, as shown in Fig. 8(a) and (b). The even-aAA stacking presents the largest (smallest) energy gap, when the ribbon width is N_a = 6m + 4 (6m). Moreover, the odd-aAA stacking owns a smaller gap in N_a = 6m + 5, but the largest energy gap lies in N_a = 6m + 3 or 6m + 1. Similarly, the even-aAA′ and odd-aAA′ stackings are each classified into one of three width-dependent energy gap categories. The even-aAA′ stackings belong to the largest energy gap among the discussed armchair systems when the ribbon width corresponds to the 6m + 4 category. The smallest energy gap of the even-aAA′ stackings is observed in the 6m + 2 category. The odd-aAA′ stacking for the 6m + 1 (6m + 3) category owns a larger (smaller) energy gap. These complex width-dependences are different from those presented in flat GNRs, mainly owing to the combined stacking and curvature effects in this unique folding structure. The ribbon width corresponding to the smallest energy gap is the 3m + 2 category for the flat GNRs; however, this is not exactly the case for the folded AGNRs. Instead, another category associated with the smallest energy gap here is 3m, for example, the even-aAA and odd-aAA′ stackings.

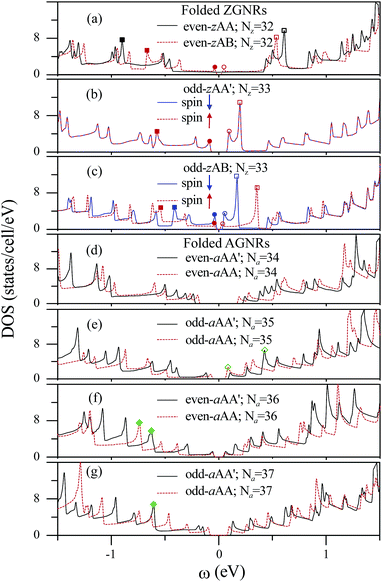
The DOS directly reflects the main characteristics of the band structures. The low-energy DOS of the even-zAA folded ZGNR, as shown in Fig. 9(a) by the black solid curve, exhibits a plateau near E_F, two prominent peaks (solid and hollow squares), and many square-root asymmetric peaks, respectively, coming from the intersecting linear bands, the partially rounded bands, and the parabolic bands (Fig. 5(c)). The constant plateau indicates the metallic behavior, as seen in a 1D armchair carbon nanotube.⁴³ The two prominent peaks on either side of E_F are mainly contributed by the local edge atoms. However, in the even-zAB stacking, the continuous plateau of the DOS is destroyed and evolves into two separate peaks (red solid and hollow circles in Fig. 9(a)), which determine a direct narrow gap. The odd-zAA′ and odd-zAB stackings possess two DOS's: one is associated with spin up (red curve) and the other is related to spin down (blue curve). The contributions are not distinguishable to DOS from the spin-up and spin-down states for the odd-zAA′ stackings (Fig. 9(b)), but are distinct for the odd-zAB ones (Fig. 9(c)). Moreover, regardless of the spin states, the energy spacings of the two adjacent prominent peaks (solid and hollow squares) are smaller in the odd-zAA′ and odd-zAB systems than in the even-zAB ones. The energy gap of the two separate peaks nearest to E_F is the largest (smallest) in the odd-zAA′ stackings (even-zAB stackings). The low-lying features in DOS are dramatically changed by the edge structure, as displayed for the folded AGNRs in Fig. 9(d)–(g). The peak energies, numbers and heights near E_F contrast sharply with those in the zigzag systems. There is no pair of prominent peaks coming from the edge atoms; on the contrary, many peaks originate from the k_x = 0 band-edge states.

Fig. 9 Density of states of (a) even-zAA and even-zAB, (b) odd-zAA′, (c) odd-zAB stacked configurations in folded ZGNRs, and DOS of folded AGNRs with AA and AA′ stacked manners for (d) N_a = 34, (e) N_a = 35, (f) N_a = 36; (g) N_a = 37.

The curvature, edge, and stacking effects, which play an important role in the energy, number, and height of peaks in DOS, can be verified by the scanning tunneling spectroscopy measurements. The tunneling conductance is roughly proportional to the DOS as a measurement reflecting the major structures. The various features of the DOS can be used to identify the type of folded GNRs. The folded ZGNRs possess a pair of prominent peaks on either side of E_F, a characteristic not reflected in the armchair systems. The DOS associated with the electron spin is the key to differentiate whether the width of the zigzag systems is even or odd. Only the even-zAA stacking has free-carrier states at E_F. The splitting of the spin degeneracy induces more peaks for the odd-zAB stackings. For the folded AGNRs, the odd-aAA, even-aAA′, even-aAA, and odd-aAA′ stackings cannot be easily identified due to the similar DOS. However, the energy gaps in DOS are a critical property in confirming the width-dependent six categories. In previous experimental measurements, the curvature effect in carbon nanotubes⁵¹ and rippled graphenes⁵² and the stacking effect in few-layer graphenes⁵³ have been verified. As expected, these two combined effects in folded AGNRs can be further examined by the STS measurements.

5 Concluding remarks

Geometric, electronic and magnetic properties of folded ZGNRs and AGNRs are thoroughly investigated by calculations based on ab initio functional theory. Eight types of stacking configurations and various ribbon widths are considered to reveal the fundamental properties, including optimal geometries, folding energies, charge densities, band structures, energy gaps and DOS. Folded GNRs show many important features, such as the constant D_c and D_f for larger ribbon widths, the destruction or creation of magnetism, the lower folding energies in the AB or AA′ stackings, the metal–semiconductor transitions, and the monotonous width-dependence of the energy gap. The predicted results could be verified by experimental measurements of scanning tunneling currents,⁵⁴ optical spectra,⁵⁵ and transport properties.⁵⁶

Geometric structure of folded GNR can be divided into the flat and curved parts; therefore, the fundamental properties are strongly dependent on the competition or cooperation among the stacking, curvature and edge effects. The even-zAB stackings or armchair AA′ stackings are the most stable stacking configurations. The electronic structures of folded GNRs in the higher-energy region possess anti-crossing bands because of the interlayer interactions and hybridization of four orbitals on the curved surface, while in the lower-energy region the energy gap and energy spacing of the band-edge states are sensitive to ribbon width and stacking configuration. The even-zAA stacking possesses intersecting linear bands and the even-zAB one is a narrow-gap semiconductor. The odd-zAA′ and odd-zAB stackings are magnetic materials. The latter has two energy gaps associated with the spin-up and spin-down states. All folded AGNRs are direct-gap semiconductors. These energy gaps exhibit a monotonic relationship, which decreases with increased ribbon width. It is worth noting that the armchair systems can be classified into six categories of width-dependent energy gaps. The width-dependencies in the folded AGNRs are different from those in flat nanoribbons. In other words, the smallest energy gap of the folded AGNRs is not necessarily associated with the N_a = 3m + 2 category. The DOS features, including the form, number, intensity and energy of the special structures, directly reflect the unique electronic properties. These rich electronic properties and various energy gaps are promising for the potential application in electronic devices.

Acknowledgements

We thank the Physics Division, National Center for Theoretical Sciences (South), and the Nation Science Council of Taiwan under Grants NSC 102-2112-M-182-002-MY3 and NSC 102-2112-M-006-007-MY3 for monetary support.

References

1. K. S. Novoselov, et al., Science, 2004, 306, 666.
2. K. S. Novoselov, et al., Nature, 2005, 438, 197.
3. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183.
4. K. S. Novoselov, et al., Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10451.
5. S. Stankovich, et al., Carbon, 2007, 45, 1558.
6. Y. Zhang, J. W. Tan, H. L. Stormer and P. Kim, Nature, 2005, 438, 201.
7. S. Y. Zhou, et al., Nat. Mater., 2007, 6, 770.
8. C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385.
9. C. Berger, et al., Science, 2006, 312, 1191.
10. K. S. Kim, et al., Nature, 2009, 457, 706.
11. D. V. Kosynkin, et al., Nature, 2009, 458, 872.
12. A. G. Cano-Márquez, et al., Nano Lett., 2009, 9, 1527.
13. S. S. Datta, D. R. Strachan, S. M. Khamis and A. C. Johnson, Nano Lett., 2008, 8, 1912.
14. L. Jiao, L. Zhang, X. Wang, G. Diankov and H. Dai, Nature, 2009, 458, 877.
15. M. V. Savoskin, et al., Carbon, 2007, 45, 2797.
16. X. Li, X. Wang, L. Zhang, S. Lee and H. Dai, Science, 2008, 319, 1229.
17. Z. Liu, K. Suenaga, P. J. Harris and S. Iijima, Phys. Rev. Lett., 2009, 102, 015501.
18. J. Zhang, J. Xiao, X. Meng, C. Monroe, Y. Huang and J. M. Zuo, Phys. Rev. Lett., 2010, 104, 166805.
19. J. Y. Huang, L. Qi and J. Li, Nano Res., 2010, 3, 43.
20. F. Liu, S. Song, D. Xue and H. Zhang, Adv. Mater., 2012, 24, 1089.
21. F. Cataldo, et al., Carbon, 2010, 48, 2596.
22. J. Yan, T. Wei, B. Shao, Z. Fan, W. Qian, M. Zhang and F. Wei, Carbon, 2010, 48, 487.
23. Y. W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2006, 97, 216803.
24. S. L. Chang, B. R. Wu, P. H. Yang and M. F. Lin, Phys. Chem. Chem. Phys., 2012, 14, 16409.
25. J. H. Wong, B. R. Wu and M. F. Lin, J. Phys. Chem. C, 2012, 116, 8271.
26. H. C. Chung, C. P. Chang, C. Y. Lin and M. F. Lin, Phys. Chem. Chem. Phys., 2016, 18, 7573.
27. Y. W. Son, M. L. Cohen and S. G. Louie, Nature, 2006, 444, 347.
28. S. L. Chang, B. R. Wu, J. H. Wong and M. F. Lin, Carbon, 2014, 77, 1031.
29. E. Cruz-Silva, et al., ACS Nano, 2013, 7, 2834.
30. G. Mpourmpakis, E. Tylianakis and G. E. Froudakis, Nano Lett., 2007, 7, 1893.
31. X. Peng, J. Zhou, W. Wang and D. Cao, Carbon, 2010, 48, 3760.
32. S. Saxena and T. A. Tyson, Carbon, 2010, 48, 1153.
33. X. Zhong, R. Pandey and S. P. Karna, Carbon, 2012, 50, 784.
34. E. Prada, P. San-Jose and L. Brey, Phys. Rev. Lett., 2010, 105, 106802.
35. Y. E. Xie, Y. P. Chen and J. X. Zhong, J. Appl. Phys., 2009, 106, 103714.
36. J. Feng, L. Qi, J. Y. Huang and J. Li, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 165407.
37. N. B. Le and L. M. Woods, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 035403.
38. W. J. Yin, Y. E. Xie, L. M. Liu, Y. P. Chen and R. Z. Wang, J. Appl. Phys., 2009, 113, 173506.
39. X. H. Zheng, L. L. Song, R. N. Wang, H. Hao, L. J. Guo and Z. Zeng, Appl. Phys. Lett., 2010, 97, 153129.
40. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
41. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
42. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
43. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
44. M. Birowska, K. Milowska and J. A. Majewski, Acta Phys. Pol., A, 2011, 120, 845.
45. W. S. Su, B. R. Wu and T. C. Leung, Comput. Phys. Commun., 2011, 182, 99.
46. C. Li and T. W. Chou, Int. J. Solids Struct., 2003, 40, 2487.
47. M. Ouyang, J. L. Huang, C. L. Cheung and C. M. Lieber, Science, 2001, 292, 702.
48. B. R. Wu, Appl. Phys. Lett., 2011, 98, 263107.
49. P. E. Lammert, P. Zhang and V. H. Crespi, Phys. Rev. Lett., 2000, 84, 2453.
50. J. Yan, C. Li, D. Zhan, D. Shen, J. L. Kuo, S. Chen and Z. Shen, Nanoscale, 2016, 8, 9102.
51. J. W. Wilder, L. C. Venema, A. G. Rinzler, R. E. Smalley and C. Dekker, Nature, 1998, 391, 59.
52. A. V. De Parga, et al., Phys. Rev. Lett., 2008, 100, 056807.
53. P. Lauffer, et al., Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 155426.
54. L. Tapasztó, G. Dobrik, P. Lambin and L. P. Biró, Nat. Nanotechnol., 2008, 3, 397.
55. A. C. Ferrari, et al., Phys. Rev. Lett., 2006, 97, 187401.
56. A. Barreiro, M. Lazzeri, J. Moser, F. Mauri and A. Bachtold, Phys. Rev. Lett., 2009, 103, 076601.

---