Multiscale simulation of shear-induced mechanical anisotropy of binary polymer blends
Shengwei Dengab,
Sanal Sebastian Payyappillyb,
Yongmin Huanga and
Honglai Liu*a
aState Key Laboratory of Chemical Engineering, Department of Chemistry, East China University of Science and Technology, Shanghai 200237, China. E-mail: hlliu@ecust.edu.cn
bFaculties of Chemical Engineering and Mechanical Engineering, Technion – Israel Institute of Technology, Haifa 3200003, Israel
First published on 20th April 2016
Abstract
Mechanical properties of polymer blends are not only determined by characteristics of individual polymer but also depend significantly on processing such as shear fields. A sequential mesoscopic simulation method was adopted to study the influence of shear processing on morphology orientation and mechanical responses. This method utilizes mesoscopic dynamic simulation (MesoDyn) for structural evolution and lattice spring model (LSM) for correlating the structure and mechanical behaviour. The dispersed phase in meso-structures moves from spherical to elliptical and then to columnar structure with the increase of shear rates. The morphology orientation leads to the anisotropy of elastic modulus. During the tensile test, different fracture processes were observed with two kinds of toughness relationship in blends which correspond to brittle phases dispersed in a ductile matrix and in reverse ductile phases dispersed in a brittle matrix. The tensile strength along shear processing direction increases with the increase of shear rates when the dispersed phase is ductile, while the strength decreases when the dispersed phase is brittle. The strength perpendicular to shear processing direction is mainly related to the soft matrix and interfacial strength. The morphologies of polymer blends at different shear rates and their corresponding mechanical behavior are well correlated by the mesoscopic simulation. The simulation results also yield guidelines to manufacture desired polymer blends with shearing process, e.g. extrusion or injection molding.
Introduction
Polymer blending is an important path to form new polymeric materials with desired performance. The macroscopic properties of polymer blends are strongly related to processing conditions especially for mechanical properties.1,2 The effects of shear flow on polymeric systems have been studied experimentally3 and theoretically4 during the last decades, e.g. both shear-induced mixing and demixing can be observed in polymer blends due to the relative relaxation times and plateau moduli of the two components.5 For common immiscible polymer blends in engineering applications, shear processing such as extruding by mechanical blending extruder usually results in the orientation6 of the phase morphologies, or fibrillation in some conditions.7 These structural changes at mesoscale8,9 are believed to be responsible for the anisotropic mechanical properties.9 In this way, the study of relationship between the meso-structure induced by various processing conditions and mechanical response is of high importance in industry.The experimental study plays a pivotal role in the field of mechanical properties of sheared polymer blends. In situ observation of deformation and fracture process10,11 to get a comprehensive picture of the effect of the microstructure on the macroscopic stress response is still a challenge. High efficient computer simulation could become an alternative tool to approach this question. In the study of mechanical behaviour of polymer materials, molecular dynamics is now one of the most popular simulation methods, and this method is adopted to reveal the mechanism of many physical phenomena at atomic or molecular scale.12–15 In this paper, simulating the deformation of polymer blends with shear processing becomes a multiscale problem with a set of unique challenges. For the purpose of efficient prediction, it is unnecessary to perform large scale computer simulations at small scales, though these small-scale methods could well predict some macroscopic properties of solids. A possible way is to use multiscale simulation method16–18 in order to balance the computational efficiency and accuracy.
Only a few works have investigated the effect of shear history on final mechanical behaviour of polymer materials by multiscale simulation. Buxton et al.19 combined Cahn–Hilliard method and lattice spring model (LSM)20–24 to study the dynamic fracture of sheared binary polymer blend and obtained some qualitative results without expensive computation. Inspired by this work, we here adopted the sequential mesoscopic simulation method25 that we proposed previously. Dynamic density functional theory embodied in MesoDyn26,27 was used to simulate the meso-structures of polymer blends processed under shear. MesoDyn is a field-based approach to obtain the structural evolution information with high computational efficiency, and this method can be easily applied in more complicated systems comparing to Cahn–Hilliard method, e.g. multicomponent composites. The output from MesoDyn served as input to the lattice spring model, a discretized method for continuum elastic media often used to simulate deformation and fracture of complicated structural systems.
This work aims to understand the effect of shear fields on the structure – mechanical properties relationship of polymer blends. For simplicity, binary polymer blends with dispersed phase separation structure were chosen as the model system. During the simulation, influence of shear rates on the structure evolution was first examined, followed by the study of the impact of toughness relationship between two components on the fracture process. Special emphasize was given on correlating the meso-structure and fracture behaviour through the evolution of fracture position.
Multiscale simulation for studying mechanical properties
The method combines the MesoDyn simulation for phase separation structures and a lattice spring model for mechanical properties. The output of the former serves as the input of the latter. The principles of these two methods were described in detail in our previous works.25,28,29 Here, we only give a brief overview of the methods and mainly focus on the different parts in the model according to current application.A. Morphology model
The dynamics of micro-phase separation at the mesoscopic level is simulated by using the MesoDyn program incorporated in the Materials Studio, version 6.0 from Accelrys. MesoDyn is based on a dynamic variant of mean-field density functional theory, which elucidates that there is a one-to-one relationship between the density distribution function of the system and the external potential field. The free energy F of an inhomogeneous liquid is a functional of density field ρ(r), and all thermodynamic functions can be derived from the free energy. The Langevin equation is used to describe the diffusion of the density field.Polymer chains are modelled as ideal independent Gaussian chains consisting of beads and a mean-field non-ideal contribution. On a coarse-grained time scale, a probability f can be assigned to a certain configuration of bead positions, correspondingly, a free energy functional F[f] can be constructed. Taking conditional minimum, the undetermined multiplier UI is just the external potential (subscript I stands for different kind of monomers). And the density functional of the free energy can be obtained as:
 | (1) |
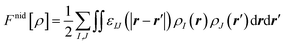 | (2) |
The intrinsic chemical potentials can be derived by functional differentiation of the free energy, μI(r) = δF/δρI(r). On the basis of these equations, the generalized time-dependent Ginzburg–Landau theory can be established. The time dependence is described by a diffusion equation. The Langevin equations for the diffusion dynamics of the density fields are then given by:
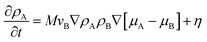 | (3) |
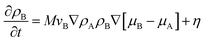 | (4) |
| 〈η(r,t)〉 = 0 | (5) |
| 〈η(r,t)η(r′,t′)〉 = −2MvBβ−1δ(t − t′)∇r·δ(r − r′)ρAρB∇r′ | (6) |
The kinetic coefficient MvBρAρB models a local exchange mechanism. The Langevin equations are constructed for an incompressible system with dynamic constraints:
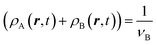 | (7) |
B. Lattice spring model
Born LSM is a numerical technique for discretizing the linear elasticity theory. The material is represented by a network of springs that occupy the nearest and next nearest neighbour bonds of a simple cubic lattice (18 in total). Although this model lacks rotational invariance, it is valid in the study of heterogeneous systems as the next nearest neighbour's central and bond-bending interactions can be locally changed to account for local variations in the elastic modulus. Importantly, this model allows us to determine micromechanical properties in a computationally efficient way.The energy associated with a node m in the cubic lattice was taken to be of the form
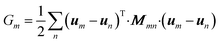 | (8) |
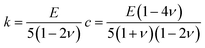 | (9) |
The elastic force acting on the mth node is a linear function of the displacement because of the harmonic form of energy in eqn (8). The force acting on the mth node, due to the local displacement of the spring between nodes m and all neighbouring n, is given by
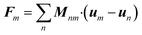 | (10) |
If the external forces are applied to the boundary nodes with the spring constants specified, the constraint that all these linear forces must balance at each node at equilibrium results in a set of sparse linear equations. The solution of these equations is obtained by using a conjugate gradient method to find the equilibrium configuration corresponding to the situation without net force at each node. The stress and strain tensors were calculated using the forces and displacements. The ijth component of the stress tensor σm,ij acting on the central node m of a cubic unit cell is defined as
 | (11) |
 represent a sum over all the cube surfaces across node m, while pijm,s is a unit vector with its components either normal or parallel to the surface s, and A is the area of surface perpendicular to the spring of tensile direction in the cubic cell. The average strain and the applied stress can then be used to calculate the elastic modulus, which is defined as the stress of a material divided by its strain.
represent a sum over all the cube surfaces across node m, while pijm,s is a unit vector with its components either normal or parallel to the surface s, and A is the area of surface perpendicular to the spring of tensile direction in the cubic cell. The average strain and the applied stress can then be used to calculate the elastic modulus, which is defined as the stress of a material divided by its strain.
Aforementioned model is used to study the stress and strain distribution after deformation; this method can also be used to predict critical fracture strain and strength. Critical fracture strain is a measure of the extensibility of the material corresponding to the maximum strain that the system can sustain before catastrophic failure. We incorporated a probabilistic method into LSM to study the fracture process wherein the fracture forms with a probability proportional to the local stress. To determine when the fracture surface is to be created, a rate of failure ps(t) of a surface s at time t is introduced as follows:
 | (12) |
Assuming that a damage occurs somewhere in the system, the probability of failure, Ps(t), occurring at a given surface s is the rate associated with the surface s relative to the total rate of damage occurring throughout the material, i.e.,  , where the sum
, where the sum  is over all surfaces. The surface chosen to fracture is related to this probability. The average time interval for this failure event to occur is
is over all surfaces. The surface chosen to fracture is related to this probability. The average time interval for this failure event to occur is
 | (13) |
To initiate fracture, a constant strain rate is applied to the sample with periodic boundary condition adopted. The strain is varied in a predetermined range by a golden section method to find the crack tip (the strain error is less than 0.1%). An initial time step Δt0 is introduced; the fracture occurs if the average time interval is smaller than Δt0. After the beginning of the fracture, the applied strain rate would be increased at each iteration by a constant value. Therefore, the creation of fracture surfaces depends on the correct probability weightings in eqn (12), and the relaxation of material surrounding the propagating crack tip takes the average time interval over which the crack grows into consideration. In this manner, the deformation and fracture cease at the fracture point when the stress no longer increases with the increase of strain, and the strain and stress at this point correspond to the fracture strain and tensile strength, respectively.
Results and discussion
A. Morphology
The microphase separations of polymer blends at different shear rates are studied by MesoDyn. Binary polymer blends with blending ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 with the same chain length of eighteen were considered in this work. The thermodynamic incompatibility of two components in blends drives the polymer system into a two-phase morphology. To facilitate the mechanical analysis, we define that the Young's moduli of these two components differ sharply in the model system, where the hard phase is made up of minor component with relatively high Young's modulus, and the soft phase is made up of major component with relatively low Young's modulus. A shear force is applied during the structure evolution in MesoDyn. In the simulation, two sets of parameters should be defined: one is the chain topology in terms of repeat beads, and the other is the interaction energy between different components. The information of molecular architecture is incorporated in the collective concentration field ρ, while the Flory–Huggins interaction parameters χ can be derived from the interaction energy parameter in eqn (2). Two components are thermodynamically incompatible when the interaction parameter (repulsion) χ is larger than 0.5. The model systems here are based on PS-b-PAN block copolymer systems (PS: polystyrene; PAN: polyacrylonitrile). MesoDyn input parameter (ν−1εIJ = χIJRT) between H and S was chosen to be 4.75 kJ mol−1, where H is the abbreviation of hard phase and S represents soft phase. All MesoDyn simulations were carried out in a cubic grid with size 40 × 40 × 40 mesh cells. The grid parameter λ ≡ γμ−1 = 1.1543, where γ represents bond length, and μ is the mesh size. The compressibility parameter is equal to 10kT, and the total simulation time is 1 × 104 steps with 8 different shear rates. The time step Δt′ = 50 ns. The simulations are performed at ambient temperature 298 K which is common for mechanical test. To ensure a stable numerical algorithm, as an approximation, all bead diffusion coefficients (β−1M) are 1.0 × 10−7 cm2 s−1 in MesoDyn input parameters, where M is the bead mobility parameter. For more simulation details about the structure evolution of this system can also be found in ref. 31.
1 with the same chain length of eighteen were considered in this work. The thermodynamic incompatibility of two components in blends drives the polymer system into a two-phase morphology. To facilitate the mechanical analysis, we define that the Young's moduli of these two components differ sharply in the model system, where the hard phase is made up of minor component with relatively high Young's modulus, and the soft phase is made up of major component with relatively low Young's modulus. A shear force is applied during the structure evolution in MesoDyn. In the simulation, two sets of parameters should be defined: one is the chain topology in terms of repeat beads, and the other is the interaction energy between different components. The information of molecular architecture is incorporated in the collective concentration field ρ, while the Flory–Huggins interaction parameters χ can be derived from the interaction energy parameter in eqn (2). Two components are thermodynamically incompatible when the interaction parameter (repulsion) χ is larger than 0.5. The model systems here are based on PS-b-PAN block copolymer systems (PS: polystyrene; PAN: polyacrylonitrile). MesoDyn input parameter (ν−1εIJ = χIJRT) between H and S was chosen to be 4.75 kJ mol−1, where H is the abbreviation of hard phase and S represents soft phase. All MesoDyn simulations were carried out in a cubic grid with size 40 × 40 × 40 mesh cells. The grid parameter λ ≡ γμ−1 = 1.1543, where γ represents bond length, and μ is the mesh size. The compressibility parameter is equal to 10kT, and the total simulation time is 1 × 104 steps with 8 different shear rates. The time step Δt′ = 50 ns. The simulations are performed at ambient temperature 298 K which is common for mechanical test. To ensure a stable numerical algorithm, as an approximation, all bead diffusion coefficients (β−1M) are 1.0 × 10−7 cm2 s−1 in MesoDyn input parameters, where M is the bead mobility parameter. For more simulation details about the structure evolution of this system can also be found in ref. 31.
Due to the strong repulsion between different components and notable difference of contents, a dispersed structure (minor phase is dispersed in the major phase matrix) is formed in the system without shear, and the shearing process lead to the morphology anisotropy. In Fig. 1a, hard phase is dispersed as spherical domains in the soft matrix. With the increase of shear rates, the dispersed phase in meso-structures moves to elliptical (Fig. 1b) and then to columnar structure (Fig. 1c).
As for the interfacial area, here we randomly take two adjacent grids (grid a and b) in the x direction for example. The number of interfacial bonds in the x direction between grids a and b is given by
| Iab = min(ρaH + ρbH, ρaS + ρbS) | (14) |
Interfacial areas at different directions were calculated to evaluate the orientation effect on morphologies (Fig. 2) at different shear rates. The system without shear shows similar interfacial area in three directions. With the shear field applied in z direction, the morphology becomes anisotropic and leads to the difference of the interfacial area in different directions. The interfacial area decreases significantly with the increase of shear rates along the shear direction (z), and this value increases slightly perpendicular to the shear direction (x and y). The reason for this phenomenon is as follows. Without the shear field, isotropic morphology is formed with spherical hard phase dispersed in the soft matrix. With the increase of the shear rate, the spherical phase change to elliptical structure or columnar structure without significant change of phase domain size. In this way, the interfacial area along the shear direction is decreased and in reverse this area perpendicular to the shear direction is increased. Due to the limited box size, some deviations can be observed, e.g. systems with shear rate of 5 × 103 s−1 and 1 × 105 s−1 at x direction.
 | ||
| Fig. 2 Interfacial area corresponding to polymer blends at different shear rates (vs) (calculating along x, y or z directions). | ||
B. Mechanical properties: elastic modulus, strength and fracture process
| Em = ρHEH + ρSES | (15) |
The normal stress distribution of x–z plane (y = y/2) is shown in Fig. 3. A proper scaling factor was chosen and then applied it to all samples to rescale the stress value within the range from 0 to 1. Corresponding morphologies are shown on the top-left corner, where the hard phase domains are coloured red, and the soft matrix is displayed in blue. The stress distribution is closely related to the structure and stress mainly concentrates on the hard phase in all samples. In sample a, the hard phase is dispersed in soft matrix and separated by the soft phase. When the sample is deformed at z direction, the stress concentrate at hard phase is relieved by the soft phase. While in sample g, the hard phase run through the sample along the tensile direction and the stress in this phase cannot be delivered to the soft matrix, and then the average stress at hard phase in sample g is much higher than that in sample a. With the increase of shear rates, the hard phase moves from spherical to elliptical to columnar structure, the gap (soft phase) between hard phase domains is decreased or disappeared, it also leads to the difficulty of stress release of hard phase when the stress is applied at shear direction (z). This indicates that the stress at hard phase increases with the increase of shear rates.
When the tensile direction is parallel to the shear direction, the average stress is mainly attributed by the stress at hard phase and increases with the increase of shear rates. This average stress is related to the elastic modulus along tensile direction as the same strain is applied to different samples. From the LSM calculation (Fig. 4), when the tensile deformation is at z direction, the elastic modulus (dimensionless unit in the model system) generally increases with the increase of shear rates. When the deformation is at x or y direction (perpendicular to the direction of shear fields), the hard phase is separated by the soft phase and therefore the elastic modulus is mainly dominated by the soft matrix.32 The elastic moduli along x direction are almost the same as the moduli along y direction, and these moduli slightly decrease with the increase of shear rates. The slight decrease of modulus is caused by the increase of interfacial area and weak interface applied in the LSM calculation.28 Similar behaviour can be found in Nasir Mahmood's experiment related to shear processing on mechanical properties of styrene butadiene triblock copolymers,9 and this behaviour can also be explained by Voigit and Maxwell models33 which are usually used to correlate the structure and morphology of fiber reinforced systems.
2.1. Ductile phases disperse in a brittle matrix. As shown in Fig. 5, the black circle dot shows the trend of tensile strength (dimensionless unit in the model system) when the stretching direction is parallel to the shear direction. The strength increase slightly at low shear rates (samples with shear rate of 2 × 103 s−1, 5 × 103 s−1 and 1 × 104 s−1) comparing to the system without shear. From the stress distribution in Fig. 3, the hard phase in these three systems is dispersed in the soft matrix in the form of ellipsoids. With the further increase of shear rates, the hard phase turn to columnar structure and run though the simulation box, and the strength dramatically increases at high shear rates (samples with shear rate of 1 × 104 s−1, 5 × 104 s−1 and 1 × 105 s−1). The increase of elastic modulus is contributed by the orientation of hard phase and the fracture is mainly happened in the soft phase based on the assumption of the minimum fracture stress. When the stress concentrates in the hard phase, the stress of the soft phase is relaxed and lead to higher fracture strain, and the increase of elastic modulus will also lead to the increase of strength. A brittle–ductile transition34 is observed here. The red triangle dot shows the trend of tensile strength when the tensile direction is perpendicular to the shear direction (here we only choose y direction due to the slight difference of the result when the tensile test at x or y direction). The tensile strengths for different samples are almost the same in this case. The elastic modulus is controlled by the soft phase and the fracture is also occurred in this phase. It means that the stress is not concentrated in the hard phase and fracture strains for all samples are similar. And then the tensile strength maintains the same with the increase of shear rates.
In order to study the fracture creation, the coordinates for every fracture positions were recorded for further analysis. Each broken bond represents the removal of a cluster of springs and the creation of a fracture surface.19 We then depict the fractions of fracture number for the hard phase, soft phase and interphase which are the average value after removal of 80 clusters of springs for all polymer blends. The fracture fraction is the average composition of all beads connected by broken springs, which is used to determine the relative contribution of fracture of difference phases. Fig. 6 shows the fracture fraction when the stretch direction is perpendicular to the shear direction. The fracture is mainly happened in the brittle soft phase, while the fracture in the interface can be observed in some samples. The fracture will occasionally occur in the interface area due to the weak interface strength applied in LSM. This phenomenon can be explained by the pull out of polymer chains35 in the interface of immiscible polymer blends, while the effect of interface strength on the mechanical behaviour was studied in our previous work.28
 | ||
| Fig. 6 Fracture fractions at different shear rates (vs). The stretch direction is perpendicular to the shear direction. | ||
When the stretch direction is parallel to the shear direction, the soft phase (brittle) dominates the mechanical properties. The fracture still mainly happens in the soft phase (Fig. 7) for all samples, which agrees well with the assumption that ductile phases disperse in a brittle matrix. But for high shear rates samples, the fracture occurs in the hard phase and interface occasionally. With the increase of shear rates, the morphology becomes anisotropic and the stress concentrated on the hard phase will deliver to the interphase, and then the fracture will also occur in the interface due to the immiscible characteristic.
 | ||
| Fig. 7 Fracture fractions at different shear rates (vs). The stretch direction is parallel to the shear direction. | ||
2.2. Brittle phases disperse in a ductile matrix. Adding stiff polymer into soft but ductile polymer to improve its mechanical properties is an important way in developing engineering polymer materials. Fig. 8 shows the tensile strength of polymer blends when the brittle hard phase disperses in the ductile soft matrix. Similarly, the black circle dot shows the trend of tensile strength when the tensile direction is parallel to the shear direction. The strength is decreasing with the increase of shear rates in general, which is corresponding to a ductile–brittle transition process.36 The stress becomes to concentrate on the hard phase with the increase of shear rates, especially when the hard phase becomes columnar structure at high shear rates. The elastic modulus of the sample is mainly controlled by the hard phase. Due to the assumption of brittle dispersed phase and ductile matrix, stress concentration in the hard phase will lead to smaller fracture strain and lower tensile strength. The red triangle dot shows the trend of tensile strength when the tensile direction is perpendicular to the shear direction. The stress concentration in the hard phase will be relaxed by surrounding soft phase, then lead to higher fracture strain, and then the fracture will happen at both soft and hard phase. In this way, the tensile strength is unlikely to be influenced by morphology orientation.
Fig. 9 shows that when the stretch direction is perpendicular to the shear direction, the fracture will happen at both soft phase and hard phase. And it seems that the fracture position is not relevant to shear rates. The applied force is perpendicular to the orientation of hard phase, and during the tensile test, the stress concentration in hard phase will deliver to soft phase and lead to higher fracture strain. It means that the node in soft phase has larger strain and higher fracture strain (ductile) than the node in hard phase. With the increase of uniaxial strain, both phases (soft and hard) will fracture. In this way, the fracture of position is not strongly related to the shear rate, and all samples have similar fracture strain and tensile strength.
 | ||
| Fig. 9 Fracture fractions at different shear rates (vs). The stretch direction is perpendicular to the shear direction. | ||
Blending with stiff immiscible polymer as minority phase and adding nanofillers are both effective methods to improve the mechanical property of soft polymers, but nanofiller reinforced polymers can result in strong interface and unbreakable hard phase domain, e.g. polymer filled with efficiently exfoliate nanoparticles.37 In contrast, fracture can happen in the hard phase in immiscible polymer blends and the interface is usually weak due to the disentanglement in real polymers.38 Fig. 10 shows the fracture fraction when the stretch direction is parallel to the shear direction. The fracture is mainly occurring at the hard phase in samples with shear rate of 1 × 105 s−1 and 2 × 105 s−1 (around 80%). The bifurcation of the columnar structure in some highly sheared samples may happen with further fracture. And the fracture fraction in hard phase is increasing with the increase of shear rates. This phenomenon can be explained as follows, the orientation of morphology will lead to the stress concentration on the hard phase especially when the hard phase becomes columnar structure and run through the simulation box. This concentration will lead to the fracture of samples due to the brittle hard phase.
Conclusion
The mechanical properties of polymer blends with shear processing are investigated by using a combined simulation method, where MesoDyn is employed to simulate the structural evolution of polymer blends and dynamic LSM is adopted to capture static and dynamic mechanical properties. Dispersed structure was observed in the system without shear due to the repulsion and disparity of volume fraction between two components. With the addition of shear stress during the structure evolution, the morphology becomes anisotropic and finally changes to columnar structure, which corresponds to shear induced structure orientation in experiment.3 These morphologies at different shear rates were then served as the input of the upcoming mechanical test. The elastic modulus was measured at different directions by LSM and the fracture process was studied based on two kinds of toughness relationship between two components. Mechanical anisotropy is observed from the result of elastic modulus and tensile strength due to the orientated morphology. The location of the fracture was recorded along with the creation of fracture surface, which help us to understand the fracture process and correlate the meso-structure and mechanical properties. For example, the fracture is mainly occurred in the hard phase when the hard phase is brittle and the tensile direction is parallel to shear direction.Based on these results we can conclude that the morphology anisotropy at mesoscale induced by external field leads to the mechanical anisotropy. The elastic modulus is strongly related to the orientation between the applied force and shear processing, while the strength is not only mainly influenced by the orientation but also the toughness for each component and the interfacial strength. Ductile matrix with strong interface will lead to overall high strength. Weak interface which is run through the system facilitates the crack developing along the interface and results in catastrophic break at low fracture strain. These findings based on binary polymer blends system with dispersed structure indicate an example for the application of our sequential mesoscopic simulation method, and we can expand the application to more complicated structures according to real polymers, e.g. multicomponent polymer system, block copolymers, polymer nanocomposites. The extensive application make this method become more efficient to study the mechanical response of heterogeneous polymer materials without large-scale computations and show its predictive capabilities to be applied in polymer processing industry.
Acknowledgements
Financial support for this work was provided by the National Natural Science Foundation of China (No. 91334203 and 21476071), the 111 Project of Ministry of Education of China (No. B08021), the Fundamental Research Funds for the Central Universities and Technion-Guangdong Fellowship.References
- E. Martuscelli, Polymer Blends: Processing, Morphology, and Properties, Springer Science & Business Media, 2012 Search PubMed
.
- Y. Zhang, M. Zuo, Y. Song, X. Yan and Q. Zheng, Compos. Sci. Technol., 2015, 106, 39 CrossRef CAS
.
- C. Rotella, S. Tencé-Girault, M. Cloitre and L. Leibler, Macromolecules, 2014, 47, 4805 CrossRef CAS
.
- C. L. Tucker III and P. Moldenaers, Annu. Rev. Fluid Mech., 2002, 34, 177 CrossRef
.
- N. Clarke and T. McLeish, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, R3731 CrossRef CAS
.
- L. C. Arruda, M. Magaton, R. E. S. Bretas and M. M. Ueki, Polym. Test., 2015, 43, 27 CrossRef CAS
.
- R. Su, K. Jiang, Y. Ge, S. Hu, Z. Li, X. Li, K. Wang, Q. Zhang, Q. Fu and F. Yang, Polym. Int., 2011, 60, 1655 CrossRef CAS
.
- M.-C. Lu, R.-H. Chen and K.-H. Chi, Plast., Rubber Compos., 2008, 37, 29 CrossRef CAS
.
- N. Mahmood, A. M. Anton, G. Gupta, T. Babur, K. Knoll, T. Thurn-Albrecht, F. Kremer, M. Beiner and R. Weidisch, Polymer, 2014, 55, 3782 CrossRef CAS
.
- G. Stoclet, J. Lefebvre, R. Séguéla and C. Vanmansart, Polymer, 2014, 55, 1817 CrossRef CAS
.
- E. M. McCready and W. R. Burghardt, Macromolecules, 2014, 48, 264 CrossRef
.
- Z. Zheng, J. Shen, J. Liu, Y. Wu, L. Zhang and W. Wang, RSC Adv., 2016, 6, 28666 RSC
.
- T. Ge, G. S. Grest and M. O. Robbins, Macromolecules, 2014, 47, 6982 CrossRef CAS
.
- J. Shen, J. Liu, H. Li, Y. Gao, X. Li, Y. Wu and L. Zhang, Phys. Chem. Chem. Phys., 2015, 17, 7196 RSC
.
- I.-C. Yeh, J. W. Andzelm and G. C. Rutledge, Macromolecules, 2015, 48, 4228 CrossRef CAS
.
- S. Yang, S. Yu, W. Kyoung, D.-S. Han and M. Cho, Polymer, 2012, 53, 623 CrossRef CAS
.
- H. Shin, S. Yang, J. Choi, S. Chang and M. Cho, Chem. Phys. Lett., 2015, 635, 80 CrossRef CAS
.
- J. Choi, H. Shin, S. Yang and M. Cho, Compos. Struct., 2015, 119, 365 CrossRef
.
- G. A. Buxton and A. C. Balazs, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 054101 CrossRef
.
- G. A. Buxton, C. M. Care and D. J. Cleaver, Modell. Simul. Mater. Sci. Eng., 2001, 9, 485 CrossRef
.
- G. A. Buxton and A. C. Balazs, J. Chem. Phys., 2002, 117, 7649 CrossRef CAS
.
- G. A. Buxton, J. Y. Lee and A. C. Balazs, Macromolecules, 2003, 36, 9631 CrossRef CAS
.
- L.-T. Yan, E. Maresov, G. A. Buxton and A. C. Balazs, Soft Matter, 2011, 7, 595 RSC
.
- G. A. Buxton and A. C. Balazs, Macromolecules, 2005, 38, 488 CrossRef CAS
.
- S. Deng, Y. Huang, S. Xu, S. Lin, H. Liu and Y. Hu, RSC Adv., 2014, 4, 63586 RSC
.
- B. Van Vlimmeren, M. Postma, P. Huetz, A. Brisson and J. Fraaije, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 5836 CrossRef CAS
.
- J. Fraaije, B. Van Vlimmeren, N. Maurits, M. Postma, O. Evers, C. Hoffmann, P. Altevogt and G. Goldbeck-Wood, J. Chem. Phys., 1997, 106, 4260 CrossRef CAS
.
- S. Deng, X. Zhao, Y. Huang, X. Han, H. Liu and Y. Hu, Polymer, 2011, 52, 5681 CrossRef CAS
.
- S. Deng, Y. Huang, C. Lian, S. Xu, H. Liu and S. Lin, Polymer, 2014, 55, 4776 CrossRef CAS
.
- J. Fraaije, A. Zvelindovsky and G. Sevink, Mol. Simul., 2004, 30, 225 CrossRef CAS
.
- S. Piotto; S. Concilio; F. Mavelli and P. Iannelli, in Macromolecular symposia, Wiley Online Library, 2009, vol. 286, p. 25 Search PubMed
.
- Y. Cohen, R. J. Albalak, B. J. Dair, M. S. Capel and E. L. Thomas, Macromolecules, 2000, 33, 6502 CrossRef CAS
.
- I. M. Ward and J. Sweeney. An Introduction to the Mechanical properties of Solid Polymers, John Wiley & Sons, 2004, ch. 7 and 8 Search PubMed
.
- Z. Liu, X. Zhang, X. Zhu, Z. Qi and F. Wang, Polymer, 1997, 38, 5267 CrossRef CAS
.
- J. Washiyama, E. J. Kramer, C. F. Creton and C.-Y. Hui, Macromolecules, 1994, 27, 2019 CrossRef CAS
.
- D. Quintens, G. Groeninckx, M. Guest and L. Aerts, Polym. Eng. Sci., 1990, 30, 1474 CAS
.
- S. M. Liff, N. Kumar and G. H. McKinley, Nat. Mater., 2007, 6, 76 CrossRef CAS PubMed
.
- A. Phatak, L. S. Lim, C. K. Reaves and F. S. Bates, Macromolecules, 2006, 39, 6221 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2016 |






