DOI:
10.1039/C6RA07726A
(Paper)
RSC Adv., 2016,
6, 55984-55989
Microstructure, dielectric properties and impedance spectroscopy of Ni doped CaCu3Ti4O12 ceramics
Received
24th March 2016
, Accepted 6th June 2016
First published on 6th June 2016
Abstract
Ni doped CaCu3Ti4O12 ceramics (CaCu3−xNixTi4O12, x = 0, 0.05, 0.1, 0.2) were prepared by a sol–gel method and the influence on the microstructure, dielectric properties and impedance spectroscopy has been investigated. CaCu3−xNixTi4O12 ceramics can cause a remarkable increase in the grain size and exhibit a very high dielectric constant (ε′) over a wide frequency range at room temperature. The ε′ value of the CaCu2.9Ni0.1Ti4O12 ceramic sintered at 1060 °C for 8 h was between 7.1 × 104 and 9.6 × 104 over the frequency range of 20 Hz to 100 kHz. Besides, a very low dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) of 0.025 was observed for the CaCu2.95Ni0.05Ti4O12 ceramic sintered at 1060 °C for 8 h with ε′ ∼ 4.2 × 104 at about 1 kHz. These results indicate that Ni doping at the Cu site may improve the dielectric properties of CaCu3Ti4O12. The giant dielectric response behavior can be attributed to the internal barrier layer capacitance (IBLC) effect.
δ) of 0.025 was observed for the CaCu2.95Ni0.05Ti4O12 ceramic sintered at 1060 °C for 8 h with ε′ ∼ 4.2 × 104 at about 1 kHz. These results indicate that Ni doping at the Cu site may improve the dielectric properties of CaCu3Ti4O12. The giant dielectric response behavior can be attributed to the internal barrier layer capacitance (IBLC) effect.
1. Introduction
In recently years, dielectric materials with high dielectric constants (ε′) have attracted much attention due to application in the miniaturization of electronic devices, especially those with giant ε′ at a low frequency. CaCu3Ti4O12(CCTO) has recently attracted considerable attention due to its giant ε′ in the order of 104 at room temperature (RT) with a good temperature stability over a wide temperature range from 100 K to 600 K.1–11 However, an increase in ε′ is usually accompanied by a strong increase in the dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ).12 In other words, high tan
δ).12 In other words, high tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ has restricted the practical application of CCTO.
δ has restricted the practical application of CCTO.
To date, the mechanism for giant dielectric response of CCTO is still ambiguous.6 Most studies attribute the cause of the giant ε′ phenomenon to extrinsic origins. An internal barrier layer capacitance (IBLC) effect associated with insulating grain boundaries and semiconducting grains was proposed by Sinclair group.3–5 They considered that the novel giant dielectric response of CCTO comes from heterogeneities, and the explanation has been the most widely accepted one so far. According to the IBLC model, the change of electric properties of grain and grain boundary will affect the dielectric properties considerably. In other words, the dielectric properties of CCTO are very sensitive to the preparation process as well as ion-doping. For this hypothesis, many groups have tried doping CCTO with various ions, such as La for Ca,13 Ni for Cu,14–16 Nb for Ti17 etc. Among these reports, Ni substitution of Cu site seems to be a useful way.9–11 Rai et al. reported that Ni doping (CaCu2.9Ni0.1Ti4O12) could increase the ε′ from 1800 to 3000 at RT and 1 kHz. However, the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ also increased from 0.2 to about 0.25;14 Zhang et al. synthesized CaCu3NixTi4O12+x (x = 0, 0.1, 0.2, 0.3) ceramics by the sol–gel method. With x = 0.2, they found that CaCu3Ni0.2Ti4O12.2 ceramics exhibits a high ε′ about 4000 and a tan
δ also increased from 0.2 to about 0.25;14 Zhang et al. synthesized CaCu3NixTi4O12+x (x = 0, 0.1, 0.2, 0.3) ceramics by the sol–gel method. With x = 0.2, they found that CaCu3Ni0.2Ti4O12.2 ceramics exhibits a high ε′ about 4000 and a tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ about 0.4 at RT and 1 kHz;15 Li et al. prepared CCTO–xNiO ceramics by the conventional solid state reaction method. They found that, with x = 0.003 and 0.006, the ε′ could increase to 3.2 × 104 at RT at 1 kHz while the ε′ of pure CCTO is only about 1.2 × 104. On the other hand, the tan
δ about 0.4 at RT and 1 kHz;15 Li et al. prepared CCTO–xNiO ceramics by the conventional solid state reaction method. They found that, with x = 0.003 and 0.006, the ε′ could increase to 3.2 × 104 at RT at 1 kHz while the ε′ of pure CCTO is only about 1.2 × 104. On the other hand, the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ decreases obviously by Ni doping. With x = 0.020, the tan
δ decreases obviously by Ni doping. With x = 0.020, the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ was as low as 0.12 while the tan
δ was as low as 0.12 while the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ of pure CCTO is 0.34 at RT and 1 kHz.11 As described above, one can find that Ni doping can significantly change the dielectric properties of CCTO. However, both the microstructure and dielectric properties of similar Ni-doping samples prepared by different group or method were very different,14–16 indicating the cause of the giant ε′ phenomenon is extrinsic.
δ of pure CCTO is 0.34 at RT and 1 kHz.11 As described above, one can find that Ni doping can significantly change the dielectric properties of CCTO. However, both the microstructure and dielectric properties of similar Ni-doping samples prepared by different group or method were very different,14–16 indicating the cause of the giant ε′ phenomenon is extrinsic.
In our recent work, a very low tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ of 0.028 was observed in pure CCTO ceramic (prepared by the sol–gel method) sintered at 1100 °C for 16 h with ε′ ∼ 1.8 × 104 at RT and 1 kHz.18 In this paper, stoichiometric CaCu3−xNixTi4O12 (CCNTO, x = 0, 0.05, 0.1, 0.2) ceramics were successfully prepared by the sol–gel method. The influences of different Ni doping and sintering temperature/duration on the microstructures, dielectric properties and impedance spectroscopy were analyzed and discussed. Value of ε′ was extremely increased while value of tan
δ of 0.028 was observed in pure CCTO ceramic (prepared by the sol–gel method) sintered at 1100 °C for 16 h with ε′ ∼ 1.8 × 104 at RT and 1 kHz.18 In this paper, stoichiometric CaCu3−xNixTi4O12 (CCNTO, x = 0, 0.05, 0.1, 0.2) ceramics were successfully prepared by the sol–gel method. The influences of different Ni doping and sintering temperature/duration on the microstructures, dielectric properties and impedance spectroscopy were analyzed and discussed. Value of ε′ was extremely increased while value of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ considerably decreased by Ni doping. A ε′ of ∼8.7 × 104 and tan
δ considerably decreased by Ni doping. A ε′ of ∼8.7 × 104 and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ of ∼0.047 have been achieved for CaCu2.9Ni0.1Ti4O12 ceramics sintered at 1060 °C for 8 h in the atmosphere measured at RT and 1 kHz. And a very low tan
δ of ∼0.047 have been achieved for CaCu2.9Ni0.1Ti4O12 ceramics sintered at 1060 °C for 8 h in the atmosphere measured at RT and 1 kHz. And a very low tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ ∼ 0.025 was found in the CaCu2.95Ni0.05Ti4O12 ceramics sintered at 1060 °C for 8 h with ε′ ∼ 4.2 × 104 at RT and 1 kHz. In comparison with the previous work of Ni doped CCTO,14–16 the CCNTO ceramics in our work can show higher ε′ and lower tan
δ ∼ 0.025 was found in the CaCu2.95Ni0.05Ti4O12 ceramics sintered at 1060 °C for 8 h with ε′ ∼ 4.2 × 104 at RT and 1 kHz. In comparison with the previous work of Ni doped CCTO,14–16 the CCNTO ceramics in our work can show higher ε′ and lower tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, which may be related to the preparation and sintering process.
δ, which may be related to the preparation and sintering process.
2. Experimental
CaCu3−xNixTi4O12 (x = 0, 0.05, 0.1, 0.2) powders were prepared by the sol–gel method. Appropriate amount of calcium nitrate (Ca(NO3)2·4H2O, 99%), nickel nitrate (NiNO3·6H2O, 99%), copper nitrate (Cu(NO3)2·3H2O, 99%), tetrabutyl titanate ([CH3(CH2)3O]4Ti, 99%) and citric acid (C6H8O7, 98.5%), all from aladdin, were weighted in precision and dissolved in ethanol to be mixed uniformly (the pH value needs to be adjusted to 2–3 with nitric acid). After magnetic stirring, homogeneous sol was obtained. The gel was obtained by stirring the sol at 80 °C for about 3 h and dried at 100 °C for about 16 h. The CCNTO precursor powders were obtained by sintering the gel at 650 °C for 2 h in air. Then, the precursor was fully grounded and pressed into small pellets (12 mm in diameter, 2 mm in thickness) with a pressure of 350 MPa. Finally, the pellets were sintered at 1000–1060 °C in a muffle furnace for 8 h to get the CCNTO ceramic samples.
X-ray diffraction with Cu Kα radiation (XRD) (MSAL-XD2) and scanning electronic microscope (SEM) (HITACHI S-520) were used to characterize the phase composition and fractured cross-sectional microstructures. The step size is 0.05° and the scan speed is 6° min−1. Both surfaces of the CCNTO ceramics for dielectric measurements were coated with silver paste as the electrode. The dielectric properties were measured by an LCR meter (Agilent E4980A) with an oscillation voltage of 0.5 V over the frequency range from 20 Hz to 2 MHz and temperature range from 20 °C to 360 °C.
3. Results and discussion
Fig. 1 shows the XRD patterns for different Ni-doped CCNTO ceramic samples sintered at 1060 °C for 8 h. Ni has successfully substituted Cu atom in CCTO due to no second phase was observed. The lattice parameters are calculated to be 7.379 Å, 7.374 Å, 7.385 Å and 7.379 Å for the CaCu3−xNixTi4O12 ceramic samples with x = 0, 0.05, 0.1 and 0.2 sintered at 1060 °C for 8 h, respectively. Lattice parameters nearly remain unchanged due to the ionic radius of Ni2+ (0.72 Å) is almost the same as Cu2+ (0.71 Å). Fig. 2(a)–(d) shows the SEM images of the fractured surfaces of CaCu2.95Ni0.05Ti4O12 ceramics sintered at 1000–1060 °C for 8 h, respectively. Though the lattice parameter does not changed a lot, the grain size is influenced by Ni doping in a significant manner. The average grain size (estimated by a line intercept technique) and relative densities (by the Archimedes' method) of CCNTO ceramic samples discussed in this work are listed in Table 1.
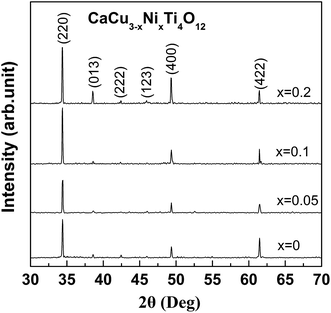 |
| | Fig. 1 The X-ray diffraction patterns of CaCu3−xNixTi4O12 (x = 0, 0.05, 0.1 and 0.2) ceramics sintered at 1060 °C for 8 h. | |
 |
| | Fig. 2 The FE-SEM images of the fractured surfaces of CaCu2.95Ni0.05Ti4O12 ceramics sintered at (a) 1000 °C, (b) 1020 °C, (c) 1040 °C, (d) 1060 °C for 8 h. | |
Table 1 The average grain size and relative densities for CaCu3−xNixTi4O12 ceramics
| Sintering temperature/duration |
Ni dopant concentration |
Average grain size (μm) |
Relative density (%) |
| 1000 °C/8 h |
x = 0.05 |
2.65 |
80.2% |
| 1020 °C/8 h |
2.74 |
81.4% |
| 1040 °C/8 h |
5.19 |
82.8% |
| 1060 °C/8 h |
6.53 |
84.0% |
| 1060 °C/8 h |
x = 0 |
1.68 |
89.5% |
| x = 0.05 |
2.74 |
84.0% |
| x = 0.1 |
31.5 |
89.5% |
| x = 0.2 |
1.77 |
88.1% |
As Sinclair et al. reported in their work,3–5 the one-step IBLC model is widely accepted as an effective method to explain the dielectric properties of CCTO. And the ε′ of CCTO samples can be approximated by the equation as follows.5,19,20
| |
 | (1) |
where
εr and
εgb represent the
ε′ of the samples and grain boundary, respectively.
A and
t represent the average grain size of semiconducting grains and the average thickness of grain boundaries, respectively.
Eqn (1) provides the general guidance in interpreting the dielectric responses of systems consisting of semiconducting grains and insulating boundaries.19,20 According to eqn (1), if one can achieve a high  ratio by controlling the grain size and the thickness of grain boundaries, a material with an extremely high ε′ can be obtained. Fig. 3(a) and (b) illustrates the frequency dependence of ε′ and tan
ratio by controlling the grain size and the thickness of grain boundaries, a material with an extremely high ε′ can be obtained. Fig. 3(a) and (b) illustrates the frequency dependence of ε′ and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ for CaCu2.95Ni0.05Ti4O12 ceramics sintered at 1000–1060 °C for 8 h measured at RT, respectively. Combining the Fig. 2, 3(a) and the data in Table 1, one can find that the trend of average grain size was nearly the same as the ε′. In addition, an equivalent circuit model has been proposed to clarify the dielectric properties of CCTO. The equivalent circuit contains three RC elements (RgCg, RgbCgb, and RxCx, respectively) and a frequency dependent term ZUDR, which represents the effect of hopping conduction of localized charge carriers.21 In order to explain the behavior of tan
δ for CaCu2.95Ni0.05Ti4O12 ceramics sintered at 1000–1060 °C for 8 h measured at RT, respectively. Combining the Fig. 2, 3(a) and the data in Table 1, one can find that the trend of average grain size was nearly the same as the ε′. In addition, an equivalent circuit model has been proposed to clarify the dielectric properties of CCTO. The equivalent circuit contains three RC elements (RgCg, RgbCgb, and RxCx, respectively) and a frequency dependent term ZUDR, which represents the effect of hopping conduction of localized charge carriers.21 In order to explain the behavior of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ for different CCNTO samples, the typical Cole–Cole plots of impedance are shown in Fig. 4. To make it clearer, the curves are amplified in the inset of Fig. 4. According to the IBLC model, the tan
δ for different CCNTO samples, the typical Cole–Cole plots of impedance are shown in Fig. 4. To make it clearer, the curves are amplified in the inset of Fig. 4. According to the IBLC model, the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ at low frequency mainly rests with the equation as follow16
δ at low frequency mainly rests with the equation as follow16
| |
tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ ≈1/ωRgbCp δ ≈1/ωRgbCp
| (2) |
where
Rgb represents the resistance of insulating grain boundary, which can be obtained by the extrapolated intercept of the arc on the
Z′ axis at the low-frequency, while
Cp is the capacitance of the sample, which is proportional to the value of
ε′ which depends on
eqn (1). It can be seen from
Fig. 4 that
Rgb increases with the increasing sintering temperature. Since another factor
Cp (∝
ε′) also increases with the increasing sintering temperature (
Fig. 3(a)), the lower value of tan
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ
δ for the sample sintered at 1060 °C for 8 h at low frequency should be caused by the increase of both factors. At the range of high frequency, the tan
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ
δ is approximately to be
16,22| |
tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ ≈ ωRgCp δ ≈ ωRgCp
| (3) |
where
Rg represents the resistance of the semiconducting grain, which can be estimated by another nonzero intercept on the
Z′ axis shown in the inset of
Fig. 4. It can be seen that the
Rg of all samples changes within a relatively small range from 0 to 5 Ω cm. Therefore,
Cp with remarkable change shown in
Fig. 3(a) is considered as a predominant factor at high frequencies in
eqn (3). Reviewing the changes of
ε′ at high frequency shown in
Fig. 3(a), the values increased with the increasing sintering temperature. These can explain why the tan
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ
δ value of the ceramics sintering at 1040 °C and 1060 °C is larger than those ceramics sintered at lower temperature, as shown in
Fig. 3(b). The results confirm a good correlation between tan
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ
δ and
ε′ at high frequencies.
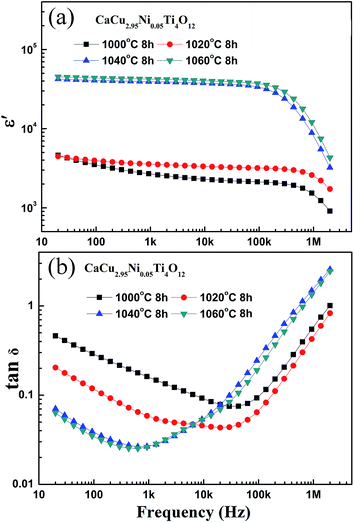 |
| | Fig. 3 The frequency dependence of ε′ (a) and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ (b) for CaCu2.95Ni0.05Ti4O12 ceramics sintered at 1000–1060 °C for 8 h. δ (b) for CaCu2.95Ni0.05Ti4O12 ceramics sintered at 1000–1060 °C for 8 h. | |
 |
| | Fig. 4 The complex impedance spectroscopies for CaCu2.95Ni0.05Ti4O12 ceramics sintered at 1000–1060 °C for 8 h. | |
Fig. 5(a)–(d) shows the SEM images of the fractured surfaces of CaCu3−xNixTi4O12 (x = 0, 0.05, 0.1, 0.2) ceramics sintered at 1060 °C for 8 h, respectively. One can clearly find that Ni doping was benefit for the grain growth of CCTO (see Table 1), and the ceramic with x = 0.1 owned the largest grain size. However, the relative density did not increase significantly as the grain size which may be caused by the increasing porosity resulting from Ni doping (see Fig. 5). Moreover, the sintering temperature which may be adjusted by the amount of Ni doping can be another reason. In future work, we will try treating CCNTO ceramics for longer time in order to reduce the porosity. Fig. 6(a) and (b) illustrates the frequency dependence of ε′ and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ for CaCu3−xNixTi4O12 (x = 0, 0.05, 0.1, 0.2) ceramics sintered at 1060 °C for 8 h measured at RT, respectively. At 1 kHz, the ε′ value is about 1.3 × 104, 4.2 × 104, 8.8 × 104 and 5.3 × 104 for CaCu3−xNixTi4O12 (x = 0, 0.05, 0.1, 0.2) ceramics, respectively, indicating Ni doping not only increases the grain size but also extremely increase the ε′. The trend of grain size was found to be nearly the same as the ε′ (see Fig. 5 and 6(a)), which can be explained by eqn (1).
δ for CaCu3−xNixTi4O12 (x = 0, 0.05, 0.1, 0.2) ceramics sintered at 1060 °C for 8 h measured at RT, respectively. At 1 kHz, the ε′ value is about 1.3 × 104, 4.2 × 104, 8.8 × 104 and 5.3 × 104 for CaCu3−xNixTi4O12 (x = 0, 0.05, 0.1, 0.2) ceramics, respectively, indicating Ni doping not only increases the grain size but also extremely increase the ε′. The trend of grain size was found to be nearly the same as the ε′ (see Fig. 5 and 6(a)), which can be explained by eqn (1).
 |
| | Fig. 5 The FE-SEM images of the fractured surfaces of CaCu3−xNixTi4O12 ceramics with (a) x = 0, (b) x = 0.05, (c) x = 0.1 and (d) x = 0.2 sintered at 1060 °C for 8 h. | |
 |
| | Fig. 6 The frequency dependence of ε′ (a) and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ (b) for CaCu3−xNixTi4O12 (x = 0, 0.05, 0.1 and 0.2) ceramics sintered at 1060 °C for 8 h. δ (b) for CaCu3−xNixTi4O12 (x = 0, 0.05, 0.1 and 0.2) ceramics sintered at 1060 °C for 8 h. | |
Until now, the greatest challenge for CCTO ceramics is to lower the dielectric loss and keep a high dielectric constant.23 The effect of sintering temperature on tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ was shown in Fig. 3(b), a very low tan
δ was shown in Fig. 3(b), a very low tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ value ∼ 0.025 was found at the CaCu2.95Ni0.05Ti4O12 ceramic sintered at 1060 °C for 8 h with ε′ ∼ 4.2 × 104 at about 1 kHz. For the ceramic sintered at 1040 °C, the two values are 0.026 and 4.0 × 104, not very different from the ceramic sintered at 1060 °C. The effect of different Ni doping ratio on the tan
δ value ∼ 0.025 was found at the CaCu2.95Ni0.05Ti4O12 ceramic sintered at 1060 °C for 8 h with ε′ ∼ 4.2 × 104 at about 1 kHz. For the ceramic sintered at 1040 °C, the two values are 0.026 and 4.0 × 104, not very different from the ceramic sintered at 1060 °C. The effect of different Ni doping ratio on the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ can be observed in Fig. 6(b). One can find that, sintering at the same condition, at low frequency (f < 2 kHz), the tan
δ can be observed in Fig. 6(b). One can find that, sintering at the same condition, at low frequency (f < 2 kHz), the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ of CaCu2.95Ni0.05Ti4O12 ceramic can be lower than pure CCTO; whereas the other two Ni doping ceramics increased the tan
δ of CaCu2.95Ni0.05Ti4O12 ceramic can be lower than pure CCTO; whereas the other two Ni doping ceramics increased the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ at almost the whole frequency range. The temperature dependence of ε′ and tan
δ at almost the whole frequency range. The temperature dependence of ε′ and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ measured at some typical frequencies for the CaCu2.95Ni0.05Ti4O12 ceramic sintered at 1060 °C for 8 h are plotted in Fig. 7. There is an obvious dielectric relaxation at low temperature in both the ε′–T and tan
δ measured at some typical frequencies for the CaCu2.95Ni0.05Ti4O12 ceramic sintered at 1060 °C for 8 h are plotted in Fig. 7. There is an obvious dielectric relaxation at low temperature in both the ε′–T and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ–T plots, and a high temperature dielectric relaxation probably existed which is out of the temperature range of measurement (ε′–T plots). The characteristic temperature increases with the increasing measurement frequency. As reported in the previous work, the high temperature relaxation is closely related to the high temperature conductivity according to the almost same activation energy.24
δ–T plots, and a high temperature dielectric relaxation probably existed which is out of the temperature range of measurement (ε′–T plots). The characteristic temperature increases with the increasing measurement frequency. As reported in the previous work, the high temperature relaxation is closely related to the high temperature conductivity according to the almost same activation energy.24
 |
| | Fig. 7 The temperature dependence of ε′ (a) and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ (b) for the CaCu2.95Ni0.05Ti4O12 ceramic sintered at 1060 °C for 8 h measured at some typical frequencies. δ (b) for the CaCu2.95Ni0.05Ti4O12 ceramic sintered at 1060 °C for 8 h measured at some typical frequencies. | |
4. Conclusions
CaCu3−xNixTi4O12 ceramics were prepared by the sol–gel method, and then sintered at various temperatures and durations. The dielectric properties as well as microstructure of CCTO were successfully improved by Ni doping, and Ni doping lead to increased porosity which may be due to the fact that the sintering time is not long enough. CaCu2.9Ni0.1Ti4O12 ceramic sintered at 1060 °C for 8 h exhibited very high ε′ (7.1 × 104 to 9.6 × 104) over the frequency range of 20 Hz to 100 kHz. The CaCu2.95Ni0.05Ti4O12 ceramic sintered at 1060 °C for 8 h show both a very low tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ ∼ 0.025 and a very high ε′ ∼ 4.2 × 104 at RT and 1 kHz. Correspondingly, dielectric relaxations can be observed in ε′/tan
δ ∼ 0.025 and a very high ε′ ∼ 4.2 × 104 at RT and 1 kHz. Correspondingly, dielectric relaxations can be observed in ε′/tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ–T curves, and ε′ tends to be slightly dependent on temperature at high frequency.
δ–T curves, and ε′ tends to be slightly dependent on temperature at high frequency.
Acknowledgements
This work was supported by National Natural Science Foundation of China (NSFC) (No. 11404236), Special Funds of the National Natural Science Foundation of China (No. 11547176) and Natural Science Foundation of Shanxi (No. 2015021026).
References
- M. A. Subramanian, D. Li, N. Duan, B. A. Reisner and A. W. Sleight, High Dielectric Constant in ACu3Ti4O12 and ACu3Ti3FeO12 Phases, J. Solid State Chem., 2000, 151, 323–325 CrossRef CAS.
- A. P. Ramirez, M. A. Subramanian, M. Gardel, G. Blumberg, D. Li, T. Vogt and S. M. Shapiro, Giant dielectric constant response in a copper–titanate, Solid State Commun., 2000, 115, 217–220 CrossRef CAS.
- T. B. Adams, D. C. Sinclair and A. R. West, Characterization of grain boundary impedances in fine- and coarse-grained CaCu3Ti4O12 ceramics, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 094124 CrossRef.
- D. C. Sinclair, T. B. Adams, F. D. Morrison and A. R. West, CaCu3Ti4O12: one-step internal barrier layer capacitor, Appl. Phys. Lett., 2002, 80, 2153 CrossRef CAS.
- T. B. Adams, D. C. Sinclair and A. R. West, Giant Barrier Layer Capacitance Effects in CaCu3Ti4O12 Ceramics, Adv. Mater., 2002, 14, 1321–1323 CrossRef CAS.
- C. C. Homes, T. Vogt, S. M. Shapiro, S. Wakimoto and A. P. Ramirez, Optical response of high-dielectric-constant perovskite-related oxide, Science, 2001, 293, 673–676 CrossRef CAS PubMed.
- Z. M. Dang, T. Zhou, S. H. Yao, J. K. Yuan, J. W. Zha, H. T. Song, J. Y. Li, Q. Chen, W. T. Yang and J. Bai, Advanced Calcium Copper Titanate/Polyimide Functional Hybrid Films with High Dielectric Permittivity, Adv. Mater., 2009, 21, 2077–2082 CrossRef CAS.
- L. Zhang, X. Shan, P. Wu, J. Song and Z. Y. Cheng, Microstructure and Dielectric Properties of CCTO-P(VDF-TrFE) Nanocomposites, Ferroelectrics, 2010, 405, 92–97 CrossRef CAS.
- W. Yang, S. Yu, R. Sun and R. Du, Nano- and microsize effect of CCTO fillers on the dielectric behavior of CCTO/PVDF composites, Acta Mater., 2011, 59, 5593–5602 CrossRef CAS.
- L. Zhang, X. Shan, P. Wu and Z. Y. Cheng, Dielectric characteristics of CaCu3Ti4O12/P(VDF-TrFE) nanocomposites, Appl. Phys. A, 2012, 107, 597–602 CrossRef CAS.
- L. J. Romasanta, P. Leret, L. Casaban, M. Hernández, M. A. de la Rubia, J. F. Fernández, J. M. Kenny, M. A. Lopez-Manchado and R. Verdejo, Towards materials with enhanced electro-mechanical response: CaCu3Ti4O12–polydimethylsiloxane composites, J. Mater. Chem., 2012, 22, 24705 RSC.
- P. Thongbai, K. Meeporn, T. Yamwong and S. Maensiri, Extreme effects of Na doping on microstructure, giant dielectric response and dielectric relaxation behavior in CaCu3Ti4O12 ceramics, Mater. Lett., 2013, 106, 129–132 CrossRef CAS.
- S. Jin, H. Xia and Y. Zhang, Effect of La-doping on the properties of CaCu3Ti4O12 dielectric ceramics, Ceram. Int., 2009, 35, 309–313 CrossRef CAS.
- A. K. Rai, K. D. Mandal, D. Kumar and O. Parkash, Characterization of nickel doped CCTO: CaCu2.9Ni0.1Ti4O12 and CaCu3Ti3.9Ni0.1O12 synthesized by semi-wet route, J. Alloys Compd., 2010, 491, 507–512 CrossRef CAS.
- C.-H. Zhang, K. Zhang, H.-X. Xu, Q. Song, Y.-T. Yang, R.-H. Yu, D. Xu and X.-N. Cheng, Microstructure and electrical properties of sol–gel derived Ni-doped CaCu3Ti4O12 ceramics, Trans. Nonferrous Met. Soc. China, 2012, 22, s127–s132 CrossRef.
- T. Li, J. Chen, D. Liu, Z. Zhang, Z. Chen, Z. Li, X. Cao and B. Wang, Effect of NiO-doping on the microstructure and the dielectric properties of CaCu3Ti4O12 ceramics, Ceram. Int., 2014, 40, 9061–9067 CrossRef CAS.
- P. Leret, M. A. de la Rubia, J. J. Romero, J. De Frutos and J. F. Fernández, Phenomenological model of grain boundary behaviour under a bias field in Nb-doped CaCu3Ti4O12 ceramics, J. Alloys Compd., 2011, 509, 9719–9723 CrossRef CAS.
- L. Sun, Z. Wang, Y. Shi, E. S. Cao, Y. Zhang, H. Peng and L. Ju, Sol–Gel synthesized pure CaCu3Ti4O12 with very low dielectric loss and high dielectric constant, Ceram. Int., 2015, 41, 13486–13492 CrossRef CAS.
- L. Marchin, S. Guillemet-Fritsch, B. Durand, A. A. Levchenko, A. Navrotsky and T. Lebey, Grain Growth-Controlled Giant Permittivity in Soft Chemistry CaCu3Ti4O12 Ceramics, J. Am. Ceram. Soc., 2008, 91, 485–489 CrossRef CAS.
- M. H. Cohen, J. B. Neaton, L. He and D. Vanderbilt, Extrinsic models for the dielectric response of CaCu3Ti4O12, J. Appl. Phys., 2003, 94, 3299 CrossRef CAS.
- W. Hao, J. Zhang, Y. Tan, M. Zhao and C. Wang, Giant Dielectric Permittivity Properties and Relevant Mechanism of NaCu3Ti3SbO12 Ceramics, J. Am. Ceram. Soc., 2011, 94, 1067–1072 CrossRef CAS.
- Y. Yan, L. Jin, L. Feng and G. Cao, Decrease of dielectric loss in giant dielectric constant CaCu3Ti4O12 ceramics by adding CaTiO3, Mater. Sci. Eng., B, 2006, 130, 146–150 CrossRef CAS.
- S. Vangchangyia, E. Swatsitang, P. Thongbai, S. Pinitsoontorn, T. Yamwong, S. Maensiri, V. Amornkitbamrung, P. Chindaprasirt and J. Hu, Very Low Loss Tangent and High Dielectric Permittivity in Pure-CaCu3Ti4O12 Ceramics Prepared by a Modified Sol–Gel Process, J. Am. Ceram. Soc., 2012, 95, 1497–1500 CrossRef CAS.
- L. Ni, X. M. Chen and X. Q. Liu, Structure and modified giant dielectric response in CaCu3(Ti1−xSnx)4O12 ceramics, Mater. Chem. Phys., 2010, 124, 982–986 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) of 0.025 was observed for the CaCu2.95Ni0.05Ti4O12 ceramic sintered at 1060 °C for 8 h with ε′ ∼ 4.2 × 104 at about 1 kHz. These results indicate that Ni doping at the Cu site may improve the dielectric properties of CaCu3Ti4O12. The giant dielectric response behavior can be attributed to the internal barrier layer capacitance (IBLC) effect.
δ) of 0.025 was observed for the CaCu2.95Ni0.05Ti4O12 ceramic sintered at 1060 °C for 8 h with ε′ ∼ 4.2 × 104 at about 1 kHz. These results indicate that Ni doping at the Cu site may improve the dielectric properties of CaCu3Ti4O12. The giant dielectric response behavior can be attributed to the internal barrier layer capacitance (IBLC) effect.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ).12 In other words, high tan
δ).12 In other words, high tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ has restricted the practical application of CCTO.
δ has restricted the practical application of CCTO.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ also increased from 0.2 to about 0.25;14 Zhang et al. synthesized CaCu3NixTi4O12+x (x = 0, 0.1, 0.2, 0.3) ceramics by the sol–gel method. With x = 0.2, they found that CaCu3Ni0.2Ti4O12.2 ceramics exhibits a high ε′ about 4000 and a tan
δ also increased from 0.2 to about 0.25;14 Zhang et al. synthesized CaCu3NixTi4O12+x (x = 0, 0.1, 0.2, 0.3) ceramics by the sol–gel method. With x = 0.2, they found that CaCu3Ni0.2Ti4O12.2 ceramics exhibits a high ε′ about 4000 and a tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ about 0.4 at RT and 1 kHz;15 Li et al. prepared CCTO–xNiO ceramics by the conventional solid state reaction method. They found that, with x = 0.003 and 0.006, the ε′ could increase to 3.2 × 104 at RT at 1 kHz while the ε′ of pure CCTO is only about 1.2 × 104. On the other hand, the tan
δ about 0.4 at RT and 1 kHz;15 Li et al. prepared CCTO–xNiO ceramics by the conventional solid state reaction method. They found that, with x = 0.003 and 0.006, the ε′ could increase to 3.2 × 104 at RT at 1 kHz while the ε′ of pure CCTO is only about 1.2 × 104. On the other hand, the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ decreases obviously by Ni doping. With x = 0.020, the tan
δ decreases obviously by Ni doping. With x = 0.020, the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ was as low as 0.12 while the tan
δ was as low as 0.12 while the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ of pure CCTO is 0.34 at RT and 1 kHz.11 As described above, one can find that Ni doping can significantly change the dielectric properties of CCTO. However, both the microstructure and dielectric properties of similar Ni-doping samples prepared by different group or method were very different,14–16 indicating the cause of the giant ε′ phenomenon is extrinsic.
δ of pure CCTO is 0.34 at RT and 1 kHz.11 As described above, one can find that Ni doping can significantly change the dielectric properties of CCTO. However, both the microstructure and dielectric properties of similar Ni-doping samples prepared by different group or method were very different,14–16 indicating the cause of the giant ε′ phenomenon is extrinsic.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ of 0.028 was observed in pure CCTO ceramic (prepared by the sol–gel method) sintered at 1100 °C for 16 h with ε′ ∼ 1.8 × 104 at RT and 1 kHz.18 In this paper, stoichiometric CaCu3−xNixTi4O12 (CCNTO, x = 0, 0.05, 0.1, 0.2) ceramics were successfully prepared by the sol–gel method. The influences of different Ni doping and sintering temperature/duration on the microstructures, dielectric properties and impedance spectroscopy were analyzed and discussed. Value of ε′ was extremely increased while value of tan
δ of 0.028 was observed in pure CCTO ceramic (prepared by the sol–gel method) sintered at 1100 °C for 16 h with ε′ ∼ 1.8 × 104 at RT and 1 kHz.18 In this paper, stoichiometric CaCu3−xNixTi4O12 (CCNTO, x = 0, 0.05, 0.1, 0.2) ceramics were successfully prepared by the sol–gel method. The influences of different Ni doping and sintering temperature/duration on the microstructures, dielectric properties and impedance spectroscopy were analyzed and discussed. Value of ε′ was extremely increased while value of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ considerably decreased by Ni doping. A ε′ of ∼8.7 × 104 and tan
δ considerably decreased by Ni doping. A ε′ of ∼8.7 × 104 and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ of ∼0.047 have been achieved for CaCu2.9Ni0.1Ti4O12 ceramics sintered at 1060 °C for 8 h in the atmosphere measured at RT and 1 kHz. And a very low tan
δ of ∼0.047 have been achieved for CaCu2.9Ni0.1Ti4O12 ceramics sintered at 1060 °C for 8 h in the atmosphere measured at RT and 1 kHz. And a very low tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ ∼ 0.025 was found in the CaCu2.95Ni0.05Ti4O12 ceramics sintered at 1060 °C for 8 h with ε′ ∼ 4.2 × 104 at RT and 1 kHz. In comparison with the previous work of Ni doped CCTO,14–16 the CCNTO ceramics in our work can show higher ε′ and lower tan
δ ∼ 0.025 was found in the CaCu2.95Ni0.05Ti4O12 ceramics sintered at 1060 °C for 8 h with ε′ ∼ 4.2 × 104 at RT and 1 kHz. In comparison with the previous work of Ni doped CCTO,14–16 the CCNTO ceramics in our work can show higher ε′ and lower tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, which may be related to the preparation and sintering process.
δ, which may be related to the preparation and sintering process.


 ratio by controlling the grain size and the thickness of grain boundaries, a material with an extremely high ε′ can be obtained. Fig. 3(a) and (b) illustrates the frequency dependence of ε′ and tan
ratio by controlling the grain size and the thickness of grain boundaries, a material with an extremely high ε′ can be obtained. Fig. 3(a) and (b) illustrates the frequency dependence of ε′ and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ for CaCu2.95Ni0.05Ti4O12 ceramics sintered at 1000–1060 °C for 8 h measured at RT, respectively. Combining the Fig. 2, 3(a) and the data in Table 1, one can find that the trend of average grain size was nearly the same as the ε′. In addition, an equivalent circuit model has been proposed to clarify the dielectric properties of CCTO. The equivalent circuit contains three RC elements (RgCg, RgbCgb, and RxCx, respectively) and a frequency dependent term ZUDR, which represents the effect of hopping conduction of localized charge carriers.21 In order to explain the behavior of tan
δ for CaCu2.95Ni0.05Ti4O12 ceramics sintered at 1000–1060 °C for 8 h measured at RT, respectively. Combining the Fig. 2, 3(a) and the data in Table 1, one can find that the trend of average grain size was nearly the same as the ε′. In addition, an equivalent circuit model has been proposed to clarify the dielectric properties of CCTO. The equivalent circuit contains three RC elements (RgCg, RgbCgb, and RxCx, respectively) and a frequency dependent term ZUDR, which represents the effect of hopping conduction of localized charge carriers.21 In order to explain the behavior of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ for different CCNTO samples, the typical Cole–Cole plots of impedance are shown in Fig. 4. To make it clearer, the curves are amplified in the inset of Fig. 4. According to the IBLC model, the tan
δ for different CCNTO samples, the typical Cole–Cole plots of impedance are shown in Fig. 4. To make it clearer, the curves are amplified in the inset of Fig. 4. According to the IBLC model, the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ at low frequency mainly rests with the equation as follow16
δ at low frequency mainly rests with the equation as follow16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ ≈1/ωRgbCp
δ ≈1/ωRgbCp
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ for the sample sintered at 1060 °C for 8 h at low frequency should be caused by the increase of both factors. At the range of high frequency, the tan
δ for the sample sintered at 1060 °C for 8 h at low frequency should be caused by the increase of both factors. At the range of high frequency, the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ is approximately to be16,22
δ is approximately to be16,22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ ≈ ωRgCp
δ ≈ ωRgCp
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ value of the ceramics sintering at 1040 °C and 1060 °C is larger than those ceramics sintered at lower temperature, as shown in Fig. 3(b). The results confirm a good correlation between tan
δ value of the ceramics sintering at 1040 °C and 1060 °C is larger than those ceramics sintered at lower temperature, as shown in Fig. 3(b). The results confirm a good correlation between tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ and ε′ at high frequencies.
δ and ε′ at high frequencies.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ (b) for CaCu2.95Ni0.05Ti4O12 ceramics sintered at 1000–1060 °C for 8 h.
δ (b) for CaCu2.95Ni0.05Ti4O12 ceramics sintered at 1000–1060 °C for 8 h.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ for CaCu3−xNixTi4O12 (x = 0, 0.05, 0.1, 0.2) ceramics sintered at 1060 °C for 8 h measured at RT, respectively. At 1 kHz, the ε′ value is about 1.3 × 104, 4.2 × 104, 8.8 × 104 and 5.3 × 104 for CaCu3−xNixTi4O12 (x = 0, 0.05, 0.1, 0.2) ceramics, respectively, indicating Ni doping not only increases the grain size but also extremely increase the ε′. The trend of grain size was found to be nearly the same as the ε′ (see Fig. 5 and 6(a)), which can be explained by eqn (1).
δ for CaCu3−xNixTi4O12 (x = 0, 0.05, 0.1, 0.2) ceramics sintered at 1060 °C for 8 h measured at RT, respectively. At 1 kHz, the ε′ value is about 1.3 × 104, 4.2 × 104, 8.8 × 104 and 5.3 × 104 for CaCu3−xNixTi4O12 (x = 0, 0.05, 0.1, 0.2) ceramics, respectively, indicating Ni doping not only increases the grain size but also extremely increase the ε′. The trend of grain size was found to be nearly the same as the ε′ (see Fig. 5 and 6(a)), which can be explained by eqn (1).

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ (b) for CaCu3−xNixTi4O12 (x = 0, 0.05, 0.1 and 0.2) ceramics sintered at 1060 °C for 8 h.
δ (b) for CaCu3−xNixTi4O12 (x = 0, 0.05, 0.1 and 0.2) ceramics sintered at 1060 °C for 8 h.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ was shown in Fig. 3(b), a very low tan
δ was shown in Fig. 3(b), a very low tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ value ∼ 0.025 was found at the CaCu2.95Ni0.05Ti4O12 ceramic sintered at 1060 °C for 8 h with ε′ ∼ 4.2 × 104 at about 1 kHz. For the ceramic sintered at 1040 °C, the two values are 0.026 and 4.0 × 104, not very different from the ceramic sintered at 1060 °C. The effect of different Ni doping ratio on the tan
δ value ∼ 0.025 was found at the CaCu2.95Ni0.05Ti4O12 ceramic sintered at 1060 °C for 8 h with ε′ ∼ 4.2 × 104 at about 1 kHz. For the ceramic sintered at 1040 °C, the two values are 0.026 and 4.0 × 104, not very different from the ceramic sintered at 1060 °C. The effect of different Ni doping ratio on the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ can be observed in Fig. 6(b). One can find that, sintering at the same condition, at low frequency (f < 2 kHz), the tan
δ can be observed in Fig. 6(b). One can find that, sintering at the same condition, at low frequency (f < 2 kHz), the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ of CaCu2.95Ni0.05Ti4O12 ceramic can be lower than pure CCTO; whereas the other two Ni doping ceramics increased the tan
δ of CaCu2.95Ni0.05Ti4O12 ceramic can be lower than pure CCTO; whereas the other two Ni doping ceramics increased the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ at almost the whole frequency range. The temperature dependence of ε′ and tan
δ at almost the whole frequency range. The temperature dependence of ε′ and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ measured at some typical frequencies for the CaCu2.95Ni0.05Ti4O12 ceramic sintered at 1060 °C for 8 h are plotted in Fig. 7. There is an obvious dielectric relaxation at low temperature in both the ε′–T and tan
δ measured at some typical frequencies for the CaCu2.95Ni0.05Ti4O12 ceramic sintered at 1060 °C for 8 h are plotted in Fig. 7. There is an obvious dielectric relaxation at low temperature in both the ε′–T and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ–T plots, and a high temperature dielectric relaxation probably existed which is out of the temperature range of measurement (ε′–T plots). The characteristic temperature increases with the increasing measurement frequency. As reported in the previous work, the high temperature relaxation is closely related to the high temperature conductivity according to the almost same activation energy.24
δ–T plots, and a high temperature dielectric relaxation probably existed which is out of the temperature range of measurement (ε′–T plots). The characteristic temperature increases with the increasing measurement frequency. As reported in the previous work, the high temperature relaxation is closely related to the high temperature conductivity according to the almost same activation energy.24
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ (b) for the CaCu2.95Ni0.05Ti4O12 ceramic sintered at 1060 °C for 8 h measured at some typical frequencies.
δ (b) for the CaCu2.95Ni0.05Ti4O12 ceramic sintered at 1060 °C for 8 h measured at some typical frequencies.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ ∼ 0.025 and a very high ε′ ∼ 4.2 × 104 at RT and 1 kHz. Correspondingly, dielectric relaxations can be observed in ε′/tan
δ ∼ 0.025 and a very high ε′ ∼ 4.2 × 104 at RT and 1 kHz. Correspondingly, dielectric relaxations can be observed in ε′/tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ–T curves, and ε′ tends to be slightly dependent on temperature at high frequency.
δ–T curves, and ε′ tends to be slightly dependent on temperature at high frequency.
