Tuning the composition of rare earth sesquioxides Gd_2−xLa_xO₃:Eu³⁺ to control phase transitions at a high temperature to design new highly sensitive luminescence-based thermal sensors

Abstract

The C-form (SG: Ia3̄) → B-form (SG: C2/m) phase transition of RE₂O₃ rare earth sesquioxides is described for the first time for face centred cubic–hexagonal close-packed array transformations. Based on XRD data analysis, the temperature of the C → B phase transition in Gd_2−xLa_xO₃ compositions (0 < x < 0.5) was controlled by adjusting the Gd/La atomic ratio and varies between 1100 °C and 1400 °C. Taking into account the various environments of rare earth oxides in C and B allotropic forms, Eu³⁺ was used as a local probe to obtain photoluminescence spectra (emission and excitation spectra, luminescence decay time curves). The spectra significantly changed during the phase transition, which occurred within a small temperature range. Furthermore, coupling Rietveld XRD data analysis for the long-range order signature with optical emission spectroscopy to probe the local environment provides a clear view of the C → B phase transition, allowing for the design of new highly sensitive thermal sensors at high temperatures.

---

1 Introduction

Rare earth sesquioxides exhibit interesting physico-chemical characteristics (low phonon energies, strong crystal fields, low thermal conductivities and high melting points), which allow for their utilization in various applications, such as optics, magnetics, electronics and catalysis.^1–4 These oxides crystallize at ambient temperatures and pressures in three polymorphs denoted as A-, B- and C-type for hexagonal, monoclinic and cubic structures, respectively. Their stability at ambient pressure and various temperatures depends on the ionic radius ratio of the cations and anions.^5–10 Large rare earth oxides based on La to Nd form hexagonal A-type structures with a P3̄m1 space group up to 600 °C.⁵ For intermediately sized cations from Sm to Gd, the corresponding sesquioxides adopt monoclinic B-type structures with a C2/m space group above 800 °C, and cubic C-type structures with a Ia3̄ space group are stabilized by Sm to form small rare earth oxides at room temperature.^5,6,11 The B-form can be obtained after quenching at high temperatures with rare earth oxides with an ionic radius between those of Sm and Gd. Considering a rare earth sesquioxide solid solution incorporating a large (La) and a small (Gd) rare earth oxide, such as Gd_2−xLa_xO₃, a phase transition from the C-form to the B-form as a function of the Gd/La ratio should be investigated, where the transition temperature would be directly related to the average rare earth ionic size. Furthermore, based on Hoekstra's diagram, this transition should occur for a restricted range of solid solutions, with the lower phase transition temperature equal to 600 °C, corresponding to a Gd/La atomic ratio near 1.2.⁵ The higher phase transition (B → C) temperature observed for Sm₂O₃ at T > 800 °C should correspond to the Gd_1.5La_0.5O₃ (Gd/La = 3) solid solution with the same average cationic radius as Sm³⁺.^12,13 From a structural point of view, the Gd₂O₃ C-form (SG: Ia3̄) corresponds to the superstructure of a fluorite-type network, where one quarter of the oxygen sites in the Td environment are removed per formula unit (Fig. 1a). In the unit cell, composed of 16 formula units (Z = 16), 8Gd³⁺ cations are on S₆ centrosymmetric (Wyckoff-8b) sites and 24 are on C₂ non-centrosymmetric (Wyckoff-24d) sites (Fig. 2a). The oxygen positions occupy 48C₁ (48e-Wyckoff) general positions in a Td environment. For the B-form (SG: C2/m (Fig. 1b)) in the unit cell, composed of 6 formula units, 12 trivalent rare earth are situated on 3 different C_s (Wyckoff-4i) sites, which correspond to one distorted octahedral site (non-centrosymmetric site) and two various seven-fold coordinated environments (Fig. 1). For B-type, the oxygen occupy four various distorted Td sites (Wyckoff-4i) and in addition to one larger Oh site (Wyckoff-2b). Taking into account their electronic configuration, the La³⁺ and Gd³⁺ cations produce non-radiative luminescence emissions, which allows for the consideration of the ternary Gd_2−xLa_xO₃ system as a white host matrix. Due to the changes in the local environment of rare earth elements during C–B phase transitions, a significant change in the europium co-doped Gd/La oxide luminescence is expected, as has been observed in pure Gd₂O₃:Eu³⁺ compounds.^11,14 For the Gd₂O₃:Eu³⁺ C-form, the nature of the predominant transition is due to the electric dipole transition ⁵D₀–⁷F₂ of the C₂ crystallographic site occupied by the Eu³⁺ ions. The contribution of the populated S₆ sites is weak and due to the magnetic dipole ⁵D₀–⁷F₁ lines. This predominant transition, due to the nature of the symmetry site, is also observed in doped Eu³⁺ Y₂O₃ and Lu₂O₃ matrix.^15–18 Due to the perturbed nature of the cationic site in the B-form with 6/7-fold coordinated non-centrosymmetric sites, the hypersensitive electric dipole transitions constitute the main part of the radiative emission. Consequently, during the C → B phase transition, a red shift in the emission is expected due to the highest contribution of non-centrosymmetric sites. Moreover, due to the increase in the coordination number from 6 to 7 during the C → B phase transition, the orbital overlap and bond covalency decrease and contribute to tuning the excitation and emission wavelengths. One should have to mention that the emission characteristics of Eu³⁺ ions have been discussed in a recent paper where a change of local symmetry is identified with a variation of photoluminescence spectra.¹⁹

Fig. 1 Representation of (a) the unit cell (cubic, SG: Ia3̄, frame in grey) closely related to the fluorite cell (cubic, SG: Fm3̄m, FCC of rare earth, frame in yellow) for the Gd₂O₃ cubic phase and (b) the unit cell (monoclinic, SG: C2/m, frame in grey) closely related to hexagonal close-packed arrays (hexagonal, SG: P6₃mc, HCP of rare earth, frame in yellow) of rare earth oxides with half of the Td sites and half of the Oh sites occupied by oxygen for the Gd₂O₃ monoclinic phase.

Fig. 2 (a) A representation of a hexagonal close-packed (ABABAB stacking) array with half of the Td sites occupied (left) by oxygens and the Gd₂O₃ monoclinic structure (right) with half of the Oh sites occupied by oxygens with a slight deviation in atoms. In this latter monoclinic unit cell (SG: C2/m), three various atomic positions of Gd³⁺ can be distinguished with three different colours (three various 4i Wyckoff positions in grey, black and green) (b) the fluorite-type network (ABCABC stacking) with all of the Td sites occupied by oxygens (left) and the Gd₂O₃ cubic structure with one quarter of the Td sites suppressed and with deviations in the atoms. In this latter cubic unit cell (SG: Ia3̄), two various atomic positions of Gd³⁺ can be distinguished with two different colours (grey 24d Wyckoff positions and green 8b Wyckoff position).

In this study, we report the structural and luminescence properties of solid solution La₂O₃–Gd₂O₃ with La < 20% mol doped by 0.5 at% of Eu³⁺. Our goal was to drive the temperature (in the high temperature range) of the phase transition as a function of the composition. The structural relationship between the two allotropic forms, B and C, are described for the first time. Then, the oxides were synthesized via self-combustion routes, followed by annealing under air at T = 700 °C. Structural investigations were performed on the undoped matrix to evaluate the optimum Gd/La ratio to reach the C → B phase transition at higher temperatures. Thereafter, complementary structural and photoluminescence characterizations were conducted on the Eu³⁺-doped matrix to finely characterize the transition phase. The final aim of this work is to design a new generation of thermal sensors that can be used at high temperatures.

2 Experimental

2.1 Powder synthesis

Oxides were prepared via a self-combustion synthesis. Typically, gadolinium and lanthanum nitrate solutions (Solvay, 99, 99%) are mixed in stoichiometric conditions. Citric acid (Sigma Aldrich, 99%) was dissolved in a solution salt with a citric acid/nitrate molar ratio equal to 1.1. The prepared mixed solutions were heated on a hot plate at 300 °C while stirring to evaporate excess water. After a few minutes, viscous liquids appeared, and self-ignited auto-combustion occurred to produce voluminous ashes. These ashes were calcined into a tubular furnace at 700 °C for 12 hours to obtain 1 g of oxide for each synthesis. Thermal treatments at higher temperatures from 900 °C to 1300 °C were performed for 20 min followed by air quenching.

2.2 X-ray diffraction

Powder X-ray diffraction patterns were collected using a Phillips X'Pert MPD X-ray diffractometer with Bragg–Brentano geometry using Kα1/Kα2 radiation (8° < 2θ < 80° step of 0.017° and a counting time of 0.6 s). Diffractograms were refined using the Rietveld method and the Fullprof package of programs with conventional reliability factors. All of the diffraction patterns were indexed based on the Gd₂O₃ cubic structure (SG: Ia3̄, ICSD # 41270) and the Gd₂O₃ monoclinic structure (SG: C2/m, ICSD # 162248) in selected papers.

2.3 Luminescence spectroscopy

Excitation and emission spectra were recorded using a SPEX Fluorolog FL212 spectrofluorometer. The excitation spectra were corrected for the variation in the incident flux, and the emission spectra were corrected for the transmission of the monochromator and the response of the photomultiplier.

3 Results and discussion

3.1 Structural relationships between the C and B phases

The C → B phase transition is classified as a reconstructive transition,^20–23 i.e., some bonds are broken and new bonds are created for the transition. However, in the literature, the structural relationships between C-cubic and B-monoclinic sesquioxides have never been described.

To better understand the phase filiation, the Gd₂O₃ phases (monoclinic and cubic) can be represented considering the primary cationic network in which the oxygens also occupy the Td and Oh sites.

In Fig. 2a and b, hexagonal close packing (ABABAB stacking) is shown, where the Td interstitial sites are half occupied by oxygens but without any Oh interstitial sites. The relationship with Gd₂O₃ monoclinic cells (B-form, SG: C2/m, Fig. 2 upper part and right) is clear, with some deviations in the atomic positions, and, in addition, the Oh interstitial sites are half occupied by oxygens leading to the final chemical formula, Gd₂O₃.

On Fig. 2 (left b), a face centred cubic (FABCABC stacking) of cations is represented with all of the Td interstitial sites filled by oxygens. For the C-cubic form of Gd₂O₃ (SG: Ia3̄, Fig. 2 right a), a quarter of the Td interstitial sites remain unoccupied, and, in addition, several atoms deviate from their standard FCC positions.

Thus, the ABCABC (FCC of rare earth) stacking of the C-form of rare earth sesquioxides evolves to ABABAB stacking (HCP of rare earth) with temperature, where oxygen atoms occupy partially Td or Oh interstitial sites. Of note, all of the atomic positions deviate from their standard FCC and HCP sites.

The FCC ↔ HCP phase transition in the case of rare earth sesquioxides, described for the first time in this study, can also be observed in various systems, such as anatase (FCC of O²⁻) ↔ rutile (HCP of O²⁻) or rock salt (FCC of S²⁻) ↔ würtzite (HCP of S²⁻).^24,25 In these latter networks, the close-packed arrays involve anions and not cations, as in the case of rare earth sesquioxides.

3.2 X-ray diffraction characterizations

Phase identifications (ICSD # 41270 for cubic-SG: Ia3̄ Gd₂O₃ and ICSD # 162248 for monoclinic SG: C2/m Gd₂O₃) of the samples annealed at 700 °C with various Gd/La contents were performed via X-ray diffraction (Fig. 3). Fig. 3 displays the XRD data of Gd_2−xLa_xO₃ (x = 0.6, 0.8, 1.2, 1.4, 1.6 and 1.8) from 15° to 45° to highlight changes in the diffraction patterns (Fig. 3). A structural change from a primarily a hexagonal phase between x = 1.4 and x = 1.2 to primarily a monoclinic phase for 0.6 ≤ x ≤ 1 was observed, whereas we only identified a pure cubic phase below x = 0.4. Finally, these XRD data indicate that the crystalline form strongly depends on the Gd/La ratio as function of the annealing treatment. The C → B → A evolution pattern of the crystalline form governed by the increase in the average cationic radius is in good agreement with the literature.^5,6 Considering x = 0.5, the average ionic size of cations is equal to that of Sm³⁺, where the C-cubic form is stabilized below T = 900 °C, and Gd_1.5La_0.5 sesquioxide is likely the limiting composition corresponding to the pure C-cubic phase.

Fig. 3 X-ray diffraction patterns of various Gd_2−xLa_xO₃ compositions annealed at 700 °C.

In the next section, we focus on the C (cubic) → B (monoclinic) phase transition. Moreover, the Gd-rich sesquioxides are non-hygroscopic compared to the La-rich phases. Two Gd-rich compositions doped with 0.5 percent Eu³⁺ (Gd_1.595La_0.395O₃:Eu_0.01³⁺ and Gd_1.795La_0.195O₃:Eu_0.01³⁺) were synthesized and annealed at various temperatures for 20 minutes followed by air quenching. As no structural evolution was observed for the samples annealed from 700 °C to 900 °C, the sample annealed at 900 °C is considered the departure reference.

Fig. 4 shows the X-ray data of the Gd_1.595La_0.395O₃:Eu_0.01³⁺ oxides annealed from 900 °C to 1300 °C at 50 °C increments. For the two lowest temperatures (900 and 950 °C), the cubic phase is observed. At higher temperatures up to 1250 °C, a C and B phase mixture is observed, indicating that a phase transition occurs. At 1300 °C, a pure monoclinic phase (B-form) is obtained. Fig. 5 shows the X-ray data of the Gd_1.795La_0.195O₃:Eu_0.01³⁺ oxide annealed under the same conditions. Similar to other composition, at low temperatures, only the cubic phase is clearly identifiable. For this latter composition, at 1200 °C, the percentage of the cubic form is more important. Higher Gd/La atomic ratios correspond to higher proportions of cubic phase at high temperatures. Above 1300 °C, the two allotropic forms are still identified on the X-ray patterns. These structural characterizations show the importance of the La/Gd atomic ratio on the thermal threshold of the phase transition. By adjusting the cationic ratio, the thermal threshold can be modulated at high temperatures between T = 1100 °C and T = 1400 °C.

Fig. 4 X-ray diffraction patterns of Gd_1.595La_0.395O₃:Eu_0.01³⁺ sesquioxides annealed at different temperatures for 20 min followed by air quenching.

Fig. 5 X-ray diffraction patterns of Gd_1.795La_0.195O₃:Eu_0.01³⁺ samples annealed at various temperatures for 20 min followed by air quenching.

For a deeper understanding, Rietveld refinements were performed based on the XRD data of Gd_1.595La_0.395O₃:Eu_0.01³⁺ obtained at various temperatures. These refinements allowed us to precisely characterize the phase transition by determining the C and B phase ratio for each annealed sample. In the first step, X-ray the diffraction data of the two pure oxides crystallizing in the C-form (sample annealed at 900 °C, SG: Ia3̄) and B-form (sample annealed at 1300 °C, SG: C2/m) were refined. The reliability factors and the atomic positions in a standard Rietveld refinement analysis were obtained by fixing the isotropic thermal factors (B_iso = 1 Å). The experimental and refined X-ray diffraction patterns of the two samples are plotted in Fig. 6, and their structural parameters are reported in Table 1. In the C-form, as mentioned in Table 1 (upper part), the rare earth atoms occupy 24d and 8b sites, whereas oxygens are located in 48e sites. The Rietveld refinement leads to satisfactory R values (R_Bragg = 3.38 & R_p = 26.2% & R_wp = 22.9%). In the B-form (Table 1, bottom), the rare earth atoms are located on three different C_s (Wyckoff-4i) sites. The oxygens occupied four different C_s (Wyckoff-4i) sites and one single C_i (Wyckoff-2b) site. Low reliability factors were obtained for this phase (R_Bragg = 6.31% & R_p = 15.4% & R_wp = 17.6%).

Fig. 6 X-ray diffraction pattern refinement of Gd_1.595La_0.395O₃:Eu_0.01³⁺ oxides annealed at 900 °C (a) and 1300 °C (b).

Table 1 Reliability factors and atomic positions of the Gd_1.595La_0.395O₃:Eu_0.01³⁺ oxides annealed at 900 °C (upper part) and 1300 °C (bottom part)

C-form, oxide annealed at 900 °C: Gd1.595La0.395Eu0.01O3 SG: Ia3̄, a = 10.873915(23) Å
Atoms	Sites	x	y	z	B (Å^2)
Gd1	24d	−0.03076(22)	0	0.25	1.0
Gd2	8b	0.25	0.25	0.25	1.0
O	48e	0.3985(19)	0.1485(23)	0.3869(25)	1.0
Rp = 26.2% & Rwp = 22.9% & RBragg = 3.38%

---

B-form, oxide annealed at 1300 °C: Gd1.595La0.395Eu0.01O3 SG: C2/m, a = 14.23654(133) Å & b = 3.61805(34) Å & c = 8.85622(82) Å & β = 100.35293(357)°
Atoms	Sites	x	y	z	B (Å^2)
Gd1	4i	0.13554(40)	0.5	0.49135(50)	1.0
Gd2	4i	0.18929(47)	0.5	0.13300(45)	1.0
Gd3	4i	0.46731(48)	0.5	0.18217(55)	1.0
O1	4i	0.13044(249)	0	0.27229(332)	1.0
O2	4i	0.32344(312)	0.5	0.02304(364)	1.0
O3	4i	0.30603(295)	0.5	0.35075(391)	1.0
O4	4i	0.47240(284)	0	0.35187(387)	1.0
O5	2	0	0.5	0	1.0
Rp = 15.4% & Rwp = 17.6% & RBragg = 6.31%

---

In the second step, Rietveld refinements were performed on the X-ray diffraction patterns for the intermediate annealed temperatures (900 < T < 1300 °C). To obtain the phase proportion, the previous structural parameters obtained for the extreme temperatures corresponding to the C- and B-forms were fixed. An example of the experimental and refined X-ray diffraction patterns of one sample containing the two forms (oxide annealed at 1200 °C) is shown in Fig. 7. The B-phase proportion as function of the temperature is described in Table 2. The R_Bragg factors associated of each C- and B-form are also presented in Fig. 7.

Fig. 7 X-ray diffraction refinement patterns of Gd_1.595La_0.395O₃:Eu_0.01³⁺ oxide annealed at 1200 °C.

Table 2 Reliability factors and atomic positions of the Gd_1.595La_0.395O₃:Eu_0.01³⁺ samples annealed at 1200 °C

T (°C)	w% B-form	RBragg (%)
		C-form	B-form
900	0	3.38	—
950	0	3.38	—
1000	Not refined	—	—
1050	Not refined	—	—
1100	16.78 ± 0.59	6.66	13.10
1150	25.58 ± 1.17	3.73	10.50
1200	86.55 ± 0.53	3.32	2.00
1250	92.56 ± 0.47	3.83	5.12
1300	100	—	6.31

---

3.3 Luminescence spectroscopy

To explore the phase transition, first, the variation in the long-range order versus annealing temperature were analysed based on XRD data. Second, the evolution of the local order as a function of the annealing temperature was probed, given the emission and excitation spectra of the Eu³⁺ ions. The general criterion is the ratio R between the intensities of EDT (Electric Dipole Transition) and MDT (Magnetic Dipole Transition) transitions. R = I(⁵D₀ → ⁷F₂)/I(⁵D₀ → ⁷F₁) gives an information on the symmetry of the sites. In this paper we have taken into account the effect of the local symmetry on the splitting of the Stark components of ⁵D₀ → ⁷F₂ transitions, with a fine study of the two following areas of this emission: range 1 600–620 nm and range 2 620–640 nm.

The emission spectra of Eu³⁺ in the two host matrices Gd_1.795La_0.195O₃ and Gd_1.595La_0.395O₃ are shown in Fig. 8 and 9, respectively. For both cases, an excitation wavelength in a charge transfer band at 250 nm was used to guarantee a high absorption of the compounds without specific selectivity of one type of europium environment. The obtained emission spectra are characteristic of the europium luminescence due to the radiative de-excitation of the excited ⁵D₀ level down to the fundamental ⁷F_J (J = 0, 1, 2, 3, 4) manifold. The ⁵D₀ → ⁷F₂ transition spectral evolutions, with temperature as a function of composition, are shown in the insets of Fig. 8 and 9. The spectral distributions of both samples annealed at low temperatures (900 °C) are similar: an intense peak at 611 nm attributed to the red hypersensitive ⁵D₀ → ⁷F₂ transitions was observed.^11,26,27 Their high intensity compared to that of the “orange” magnetic dipole transition confirmed the efficient contribution of the populated distorted site to the global emission in the C and B variety (C₂ sites of the C-form and C_s, C_i sites of the B-form). The lack of an inversion centre makes possible a partial mixing of the 4f orbitals with opposite parity 5d orbitals. For temperatures inferior to 1150 °C, independent of the composition, an improvement in the emission efficiency occurs due to an increase in crystallinity. Concerning Gd_1.595La_0.395O₃ composition, an evolution of the spectral repartition of ⁵D₀ → ⁷F₂, primarily characterized by a decrease in the most intense peak at 611 nm, was observed above 1150 °C (inset Fig. 9). For the Gd_1.795La_0.195O₃ composition, a variation in the spectrum was initiated at 1250 °C (inset Fig. 8). This clear change in the Stark component splitting of the ⁵D₀ → ⁷F₂ transitions is explained by a modification of the Eu³⁺ local environment, which is associated with the thermal C → B phase transition. The decrease in the most intense peak at 611 nm characterizes the progressive disappearance of the Eu³⁺ ions occupying the C₂ distorted prismatic sites (C-form), which move to the 6/7-fold-coordinated sites (C_s site) of the monoclinic allotropic variety (B-form). Studying the ⁵D₀ → ⁷F₂ transition evolutions of the XRD spectra highlights a dependence of the Gd/La atomic ratio on the temperature of the phase transition.

Fig. 8 Luminescence spectra of Gd_1.795La_0.195O₃:Eu_0.01³⁺ oxide annealed at various temperatures for a 250 nm wavelength excitation.

Fig. 9 Luminescence spectra of Gd_1.595La_0.395O₃:Eu_0.01³⁺ oxide annealed at various temperatures for a 250 nm wavelength excitation.

The evolution of the spectral distribution as a function of the annealing temperature for Gd_1.595La_0.395O₃:Eu_0.01³⁺ oxide is illustrated in Table 3. The 600–620 nm range (range 1) was selected as good indicator of the C-form contribution, whereas the 620–640 nm (range 2) was primarily linked to the contribution of the B-variety. The percentage of each range in the total integrated area of the electric dipole transitions is indicated. The relative contribution of each phase to the global emission was calculated by considering that the sum of the percentages of ranges 1 and 2 remains constant and equal to 100% regardless of the temperature. For each temperature, we have calculated the global integrated area (x axis in energy) below the curve in the 600–620 nm and 620–640 nm regions as the change in the spectral distribution is relevant in these two domains. We have considered that the 900 °C heat treated sample is the fingerprint of the pure C phase whereas the 1300 °C is the response of the pure B phase. As the proportion of radiative transitions between the two ranges is supposed to be fixed for each matrix (the probability remains constant), we have solved for each of the intermediary temperature a system of two equations with two unknown parameters (% C and % B).

Table 3 Spectral repartition of the partitioned ⁵D₀ → ⁷F₂ transitions

T (K)	600–620 nm (%)	620–640 nm (%)	Proportion of C (%)	Proportion of B (%)
900	78.03	21.97	100	0
950	78.74	21.26	100	0
1000	78.61	21.39	100	0
1050	76.97	23.03	100	0
1100	77.98	22.02	100	0
1150	77.13	22.87	98	2
1200	47.39	52.61	32	68
1250	37.61	62.39	11	89
1300	32.95	67.05	0	100

---

These calculations show a drastic evolution of the spectral distribution from 1150 °C, in agreement with the temperature transition phase determined previously by X-ray diffraction refinements.

Fig. 10 shows the emission spectra for an excitation at 250 nm and the excitation spectra for an emission at 615.2 nm for the Gd_1.595La_0.395O₃:Eu_0.01³⁺ composition annealed at 900 °C and 1300 °C. Under equivalent experimental conditions (same aperture slits and excitation wavelength at 250 nm), the emission graphs show similar efficiencies regarding the integrated area under the peaks. Moreover, huge differences are visible on the excitation graph. If the 4f–4f absorption lines of gadolinium remain at the same energy as expected, the charge transfer bands (CTBs), which reflect the electron transfer from the 2p oxygen orbital to the empty 4f orbitals of the Eu³⁺ ions, are not equivalent. The CTB of the C-cubic form points at near 235 nm, whereas the CTB of the B-form is red shifted and appears at 280 nm. This can be explained by the difference in the rare earth-oxygen distances in the two varieties. The rare earth-oxygen distances of the C-form (distorted prisms and octahedra) vary slightly approximately 2.33 Å (from 2.26 to 2.38 Å for the more distorted C₂ site), whereas polyhedra constituting the B-form are much more perturbed, with a longer average bond distance approximately 2.40 Å, corresponding to a less covalent chemical bond. One can count short distances of approximately 2.1 Å and long distances of 2.8 Å. As observed in oxyphosphate and oxyborate compounds doped with europium, such an environment results in the location of the CTB at a lower energy.^28,29

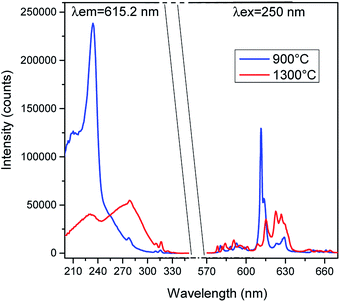Fig. 10 Excitation and luminescence spectra of Gd_1.795La_0.195O₃:Eu_0.01³⁺ oxides annealed at 900 °C and 1300 °C.

A complementary study can be performed by determining the lifetimes of each centre as function of the temperature. As illustrated in Fig. 10, the 250 nm and 615 nm wavelengths correspond to satisfying the conditions to observe ⁵D₀ → ⁷F₂ transitions of both cubic (sample annealed at 900 °C) and monoclinic (sample annealed at 1300 °C) structures. These excitation and emission conditions were selected to record the decay time curves of Eu³⁺ ions without favouring one of the crystalline forms.

All luminescence decay curves of the Gd_1.595La_0.395O₃ composition are presented in Fig. 11. These curves correspond to the radiative de-excitation of ⁵D₀ emitting levels of the Eu³⁺ down to ⁷F₂ levels in the different matrices. First, the decay time curves corresponding to the C-phase (T °C = 900 °C) and the B-phase (T °C = 1300 °C) were generated. The double exponential function, I(t) = I₀ × (A exp(−(t − t₀)/τ₁) + (1 − A) × exp(−(t − t₀)/τ₂)), was used to fit the decay curves of each sample, which corresponds to the two types of crystallographic sites for each structure (C-form: C₂ and S₆ sites; B-form: six-fold and seven-fold environment corresponding to C_s sites). Io is the fluorescence intensity at t = t₀, and τ₁ and τ₂ represent the two decay times of the ⁵D₀ excited states of the different polyhedra. The two experimental extracted lifetimes for the C-phase, τ₁ = 1.99 ± 0.02 ms and τ₂ = 4.76 ± 0.22 ms, are slightly longer than the shortest values (1.05 ms) found in the literature for the Gd₂O₃ cubic phase.¹¹ Furthermore, the presence of the two lifetimes is coherent with the presence of two different local environments for Eu³⁺ (S₆ and C₂).

Fig. 11 Photoluminescence decay time curves of the Gd_1.595La_0.395O₃:Eu_0.01³⁺ samples annealed at various temperatures for 250 nm (excitation) and 615 nm (emission) wavelengths.

Due to the selection rules, the fastest extracted lifetimes (τ₁ = 1.99 ± 0.02 ms) can be attributed to the emission of the Eu³⁺ in non-centrosymmetric C₂ sites. In fact, the longest lifetime is characteristic of the location of the Eu³⁺ ions in the S₆ centrosymmetric sites. Lifetimes of τ₃ = 1.27 ± 0.01 ms and τ₄ = 3.02 ± 0.08 ms were obtained for the B-phase sample. These lifetimes are shorter than the values determined for the C-phase sample. These results are in good agreement with the non-centrosymmetric character of an Eu³⁺ distorted environment in the B-phase. The larger τ₄ value can be attributed to the more symmetric site related to the distorted Oh environment (C_s symmetry). Note that in the experimental conditions, no discrimination can be made between the two seven-fold coordination polyhedrals. Fits of the curve were performed for various annealing temperatures. The least squares method was used to approximate the best experimental models, and the results are listed in Table 4. For intermediate temperatures between the curves that correspond to the pure C- and B-form, we fixed the values of τ₁/τ₃ and τ₂/τ₄ to obtain the relative contribution of each emission within the global decay curve. For the lifetime decay curves we have chosen non selective wavelengths: λ_exc = 250 nm because this wavelength is present in the two CTB excitation spectra of cubic and monoclinic phases and λ_emi = 615 nm because this Stark component is present in the two ⁵D₀ → ⁷F₂ spectral distributions. We have considered that the lifetimes τ₁ and τ₂ obtained for the 900 °C heat treated sample are the lifetimes of the pure C phase whereas the obtained values τ₃ and τ₄ for the 1300 °C sample are the lifetimes of the pure B phase. These lifetimes and the proportion coefficients were fixed in the fit equation, to adjust the different decay curves of the mixed phases samples the proportion of each phase were given by the fit.

Phase C (900 °C) I(t) = I₀ × (A exp(−(t − t₀)/τ₁) + (1 − A)exp(−(t − t₀)/τ₂))

Phase B (1300 °C) I(t) = I₀ × (B exp(−(t − t₀)/τ₃) + (1 − B)exp(−(t − t₀)/τ₄))

Table 4 Monoclinic phase proportion obtained after approximation based on a least squares method of the decay time curve

T °C	900	950	1000	1050	1100	1150	1200	1250	1300
M%	0	0	0	0	0	1.4	76.4	99.2	100

---

Fit mixed phases samples:

I(t) = I₀(% C[A exp(−(t − t₀)/τ₁) + (1 − A)exp(−(t − t₀)/τ₂)] + % B[B exp(−(t − t₀)/τ₃) + (1 − B)exp(−(t − t₀)/τ₄)])

τ₁, τ₂, τ₃, τ₄, A, B, t₀, being fixed the fit gives the proportion % C and % B of cubic and monoclinic phase respectively.

These curves do not exhibit significant modification until 1150 °C. Above this temperature, the curves and the relative contribution of the C-form in the total decay curve drop drastically. These changes are as well illustrated in the X-ray diffraction patterns as in the spectral distribution and reflect the C → B phase transition. The temperature threshold is equivalent for all three independent measurements.

Finally, the relative proportion of the C- and B-forms as a function of the annealing temperature determined based on three independent experimental techniques are plotted in Fig. 12 and show the trend converge for the three characterizations. Boltzmann curves were used for each case to fit the experimental points. Inflexion points characteristic of the transition phase are observed between 1150 °C and 1190 °C depending on the experimental techniques. At these high temperatures, there is only a 20 °C difference in the phase transition temperature between the XRD data, giving the evolution of the long-range order and the photoluminescence spectra data related to the variation in the local environment of Eu³⁺. Thus, Gd-rich sesquioxides with the following formulae Gd_2−xLa_xO₃:Eu³⁺ (x ≤ 0.5) are powerful and highly sensitive at high temperatures between 1100 °C and 1400 °C, and a drastic change in the emission spectra is observed during phase transitions within a small temperature range.

Fig. 12 Relative proportion of monoclinic-B phase as a function of the annealing temperature derived from the XRD Rietveld analysis, emission spectra and lifetime data. Experimental fits using the Boltzmann curve show the global tendency (full line).

4 Conclusion

The stabilization of A, B and C allotropic forms of rare earth sesquioxides as a function of pressure or temperature has been widely investigated and strongly depends on the size of the rare earth ions. In this study, we focused on the C → B transformation as a function of temperature because, on one hand, the local environments of rare earth strongly vary during the phase transition and, on the other hand, the transformation occurs at high temperatures. Thus, this C → B transformation of rare earth sesquioxides RE₂O₃ was observed for Sm, Eu and Gd with intermediate ionic sizes. Higher phase transition temperatures corresponded to smaller rare earth ionic sizes. For the first time, the C-cubic (SG: Ia3̄) → B-monoclinic (SG: C2/m) phase transition has been likened to FCC (ABCABC stacking) → HCP (ABABAB stacking) transformation involving close-packed arrays of cations (oxygens occupy interstitial Td and Oh sites). This description supports that the transformation of anatase → rutile at high temperatures involves close-packed arrays of oxygens (FCC for anatase and HCP for rutile). Gd-rich Gd_2−xLa_xO₃ sesquioxides were prepared via a self-combustion route followed by annealing under air at 700 °C to explore the C → B phase transition at high temperatures (annealing at T > 800 °C followed by quenching). The limit of stability of the cubic (C) phase was reached at x = 0.5, for which the average rare earth ionic size is similar to that of Sm³⁺. Thus, for two compositions, x = 0.2 and x = 0.4, the phase transition was analysed based on the XRD analysis. Rietveld refinement for the x = 0.4 composition allows for the accurate determination of the proportion of the B-phase as a function of temperature. Eu³⁺ ions occupying the various rare earth sites (S₆ centrosymmetric and C₂ non-centrosymmetric in the C-form, C_s non-centrosymmetric 6-fold and 7-fold coordinated sites in the B-form) were used as local probes due to the various photoluminescence and excitation spectra, which depend on the local environment of the rare earth. The emission and excitation spectra of Gd_2−xLa_xO₃:Eu³⁺ sesquioxide annealed at various temperatures and the photoluminescence decay curves were recorded. Based on the luminescence analysis, the phase transition temperature can be easily and accurately identified and varies between 1100 °C and 1400 °C in this series as a function of the La concentration. We have successfully demonstrated that control of the Gd/La atomic ratio makes possible the tuning of the transition phase temperature. X-ray diffraction characterization coupled with luminescence analyses (the study of the spectral distribution and decay time determination) leads to an efficient follow-up of the thermal history of the material synthesized through auto-combustion processes.

References

1. A. Fukabori, T. Yanagida, J. Pejchal, S. Maeo, Y. Yokota, A. Yoshikawa, T. Ikegami, F. Moretti and K. Kamada, J. Appl. Phys., 2010, 107, 073501.
2. M. Tokurakawa, K. Takaichi, A. Shirakawa, K. I. Ueda, H. Yagi, T. Yanagitani and A. A. Kaminskii, Appl. Phys. Lett., 2007, 90, 2–5.
3. T. J. Toops, A. B. Walters and M. A. Vannice, Appl. Catal., 2002, 233, 125–140.
4. X. Zhang, A. B. Walters and M. A. Vannice, Appl. Catal., 1994, 4, 237–256.
5. H. R. Hoekstra, Inorg. Chem., 1965, 5, 754–757.
6. M. Zinkevich, Prog. Mater. Sci., 2007, 52, 597–647.
7. J. O. Sawyer, B. G. Hyde and L. Eyring, Inorg. Chem., 1965, 4, 426–427.
8. B. Wu, M. Zinkevich, F. Aldinger, D. Wen and L. Chen, J. Solid State Chem., 2007, 180, 3280–3287.
9. G. Chen and J. R. Peterson, J. Alloys Compd., 1992, 186, 233–239.
10. 3 Sesquioxides, N. Hirosaki, S. Ogata and C. Kocer, J. Alloys Compd., 2003, 351, 31–34.
11. Z. Wang, P. Wang, J. Zhong, H. Liang and J. Wang, J. Lumin., 2014, 152, 172–175.
12. S. Jiang, J. Liu, C. Lin, X. Li and Y. Li, J. Appl. Phys., 2013, 113, 1–7.
13. Q. Guo, Y. Zhao, C. Jiang, W. L. Mao and Z. Wang, Solid State Commun., 2008, 145, 250–254.
14. Y. Iwako, Y. Akimoto, M. Omiya, T. Ueda and T. Yokomori, J. Lumin., 2010, 130, 1470–1474.
15. H. Forest and G. Bank, J. Electrochem. Soc., 1969, 116, 474–478.
16. M. Jia, J. Zhang, S. Lu, J. Sun, Y. Luo, X. Ren, H. Song and X. J. Wang, Chem. Phys. Lett., 2004, 384, 193–196.
17. R. G. Pappalardo and R. B. Hunt, J. Electrochem. Soc., 1985, 132, 721–730.
18. E. Zych, J. Phys.: Condens. Matter, 2002, 14, 5637–5650.
19. J. Wang, Y. Cheng, Y. Huang, P. Cai, S. Il Kim and H. J. Seo, J. Mater. Chem. C, 2014, 2, 5559.
20. C. Meyer, J. P. Sanchez and J. P. Itic, Phys. Rev. B, 1995, 51, 12187–12193.
21. Q. Guo, Y. Zhao, C. Jiang, W. L. Mao, Z. Wang, J. Zhang and Y. Wang, Inorg. Chem., 2007, 46, 6164–6169.
22. D. Lonappan, N. V. C. Shekar, T. R. Ravindran and P. C. Sahu, Mater. Chem. Phys., 2010, 120, 65–67.
23. S. Jiang, J. Liu, C. Lin, L. Bai, W. Xiao, Y. Zhang, D. Zhang, X. Li, Y. Li and L. Tang, J. Appl. Phys., 2010, 108, 083541.
24. J. Cai and N. Chen, J. Phys.: Condens. Matter, 2007, 19, 266207.
25. D. A. H. Hanaor and C. C. Sorrell, J. Mater. Sci., 2011, 46, 855–874.
26. O. Meza, E. G. Villabona-Leal, L. A. Diaz-Torres, H. Desirena, J. L. Rodríguez-López and P. Elías, J. Phys. Chem. A, 2014, 118, 1390–1396.
27. A. P. De Moura, L. H. Oliveira, I. C. Nogueira, P. F. S. Pereira, M. S. Li, E. Longo, J. A. Varela and I. L. V. Rosa, 2014, 374–388.
28. V. Jubera, J. P. Chaminade, A. Garcia, F. Guillen and C. Fouassier, J. Lumin., 2003, 101, 1–10.
29. D. C. Tuan, R. Olazcuaga, F. Guillen, A. Garcia, B. Moine and C. Fouassier, J. Phys. IV, 2005, 123, 259–263.

---