Kinetics simulation and a novel curing procedure to avoid thermal shock during the curing process of epoxy composites
Abstract
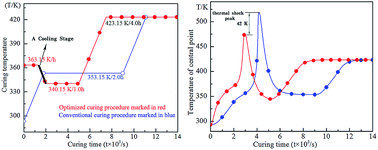
In order to reduce the effect of the thermal shock that occurs during the curing process of epoxy resin (EP), and to improve the mechanical properties of the cured EP, a novel curing procedure for an epoxy resin system, sodium carboxymethyl cellulose (CMC)/E51 type epoxy resin (E51)/4,4-diamino diphenyl methane (DDM), was established according to the simulated results of a three-dimensional finite element model and extrapolation method. Compared to the conventional curing procedure, a cooling stage was used in the new procedure according to the simulated results to reduce the effect of the thermal shock. The experimental verification showed that even when the curing time was 30 min shorter than the conventional procedure, the new curing procedure clearly improved the mechanical properties of the cured resin. For instance, the bending strength of the specimen cured by the new procedure reached 136 MPa, which is increased by 46% when compared to the specimen cured by the conventional procedure (93.3 MPa) and the impact strength increased from 18.3 kJ m−2 to 23.1 kJ m−2.

 Please wait while we load your content...
Please wait while we load your content...