Investigation of the domain structure and hierarchy in potassium–sodium niobate lead-free piezoelectric single crystals

Abstract

Recently, many techniques have been used to grow large K_0.5Na_0.5NbO₃ (KNN) based single crystals. However, most of them required the use of a crucible, fluxes in the melt at high temperature and long process times that could lead to alkali volatilization or inclusion of impurities in the crystals. In this study, the floating zone method, which is especially suitable for compounds that melt incongruently or present volatile elements, is employed to study the microstructure of [011] oriented KNN crystals. Then, the domain structure and their relationships with piezoelectric properties in KNN are investigated using scanning electron microscopy (SEM), transmission electron microscopy (TEM) and piezo force microscopy (PFM). This study reveals self-organized and hierarchized domain structures on various length scales ranging from micrometer to nanometer scale in KNN crystals. First, parallel stripe-like microdomains of 6–7 μm wide, which contain themselves parallel stripes (1–4 μm wide), are observed using SEM. These domains have been confirmed by TEM. TEM observations have also shown the presence of additional zigzag sub-microdomains with 90 and 120° orientations, which are arranged inside these observed stripes. Moreover, high resolution TEM highlighted the presence of regular antiphase boundaries at the location of the domain walls, which are caused by the small misfits between the parameters of the different structures. Split spots on the FFT image attests of these phenomena. Additionally, PFM images showed also parallel stripe-like microdomains (3–4 μm wide), which contain sub-microdomains. These sub-microdomains consist of parallel stripes of 200–400 nm and zigzag nanodomains with 60, 90, 120 and 180° orientations. The local polarization switching test by PFM emphasized that the observed domain structures correspond well with ferroelectric domains, confirming through microstructural observations the ferroelectricity of KNN. The combination of SEM, TEM and PFM observations of orthorhombic KNN crystals have shown the correlation between microstructure, sub-microstructure and domain structures at different scales. The [011] oriented KNN crystal exhibited interesting piezoelectric properties such as k_t of 0.47, d₃₃ ∼ 60–80 pm V⁻¹, ε^S_r,33 of 123, dielectric losses (δ_e) of 0.07 but also high mechanical losses (δ_m) of 0.21 that can be induced by 90° domain walls moving under the influence of an electric field during poling.

---

Introduction

The K_xNa_1−xNbO₃ (KNN) perovskite compound is of great interest due to its attractive ferroelectric and piezoelectric properties and its potential multifunctional applications, such as in ultrasonic transducers, sensors and actuators.^1–5 Indeed, the KNN family is recognized as one of the most promising lead-free materials for substituting the Pb(Zr_xTi_1−x)O₃ (PZT) family in specific applications such as those listed above. For decades KNN compositions have been extensively investigated in order to improve their piezoelectric properties through sintering condition modifications or chemical substitutions. The spark plasma sintered and hot-pressed undoped KNN ceramics showed a piezoelectric coefficient d₃₃ of 127–160 pC N⁻¹ and planar coupling factor k_p of 0.48–0.45,^6,7 respectively, while those containing substituents such as Li, Sb and Ta replacing the A and/or B perovskite sites of KNN exhibited a high thickness coupling factor k_p > 0.50 and d₃₃ > 200 pC N⁻¹.^8–10 The origin of the high piezoelectric performance of the modified KNN ceramics is ascribed to the shifting of the orthorhombic/tetragonal polymorphic phase transition (PPT) temperature from ∼200 °C near to room temperature, by means of cation substitutions that distort the KNN structure. Otherwise, Fu et al.¹¹ emphasized that the presence of nanodomains in Li, Ta and Sb co-modified KNN ceramics greatly contribute to the improvement of its piezoelectric properties. They reported domain structures consisting of nanodomains of alternate orthorhombic and tetragonal domains with a width of 20–50 nm only for compositions near polymorphic phase coexistence zone. Nanodomains easily respond to an external electric field due to their low domain wall energy, inducing thus enhanced piezoelectric properties. Similar phenomenon is observed in other lead-free compounds such as Mn-doped Na_1/2Bi_1/2TiO₃–5.5% BaTiO₃ single crystal and Ba(Zr_0.2Ti_0.8)O₃–x(Ba_0.7Ca_0.3)TiO₃ ceramics near their morphotropic phase boundary (MPB).^12,13

In the literature, abundant data can be found about the domain structure of BaTiO₃ and PbTiO₃ based materials due to their simple tetragonal structure which presents only two types of domain walls (90° and 180°).^14,15 However, limited data can be found about KNN domain morphology due to its complex orthorhombic structure which developed not only 90° and 180° domains but also 60° and 120° ones.¹⁶ The most important investigations of domain structure of KNN based materials focused on ceramics using scanning electron microscopy (SEM),¹⁷ confocal Raman microscopy (CRM),¹⁸ transmission electron microscopy (TEM),¹⁹ scanning probe microscopy²⁰ and piezo force microscopy (PFM).²¹ However, studies on KNN single crystals are rare while they could bring important informations. In recent years, the crystal growth of KNN has been the challenge to accomplish because of its incongruent melting behavior, alkali segregation and volatilization at high temperature. Chen et al.²² succeeded to grow large crystals of about 4 × 6 × 0.5 mm³ with enhanced quality in 2007, allowing thus to study their piezoelectric properties. Little attention has been paid to more fundamental aspects of crystal chemistry in KNN crystal, namely the domain structure. Thus, in 2010, ferroelectric domains in [110] and [001]-oriented Mn-doped K_0.5Na_0.5NbO₃ crystals are imaged using polarizing light microscopy (PLM).^23,24 Quite recently, Rafiq et al.²⁵ reported for the first time the domain structure of [001]-oriented K_0.5Na_0.5NbO₃ single crystals using PFM, showing a long range ordered domain pattern of parallel 180° domains with a zigzag structure of 90° domains. The piezoelectric properties are very dependent on crystallographic orientation, and it is worth noting that the domain structure of [011]-oriented K_0.5Na_0.5NbO₃ crystal has not yet been investigated using PFM. Additionally, in previous works on lead-free systems, high resolution transmission electron microscopy (HRTEM) was used to investigate Mn-doped Na_1/2Bi_1/2TiO₃–5.5% BaTiO₃ (Mn-NBT–BT) and Mn-doped Na_0.5Bi_0.5TiO₃ (Mn-NBT) ferroelectric domain walls.^12,26 For orthorhombic ferroelectrics, such as K_0.5Na_0.5NbO₃, only domain walls of KNbO₃ have been characterized by HRTEM.²⁷ Therefore, a careful investigation by HRTEM and PFM of the domain structure in [011]-oriented orthorhombic K_0.5Na_0.5NbO₃ crystals appears as important to bring some new bricks to the knowledge of the relations between microstructure, domain structures and piezoelectric properties in this KNN materials family.

Under above circumstances, we investigated the domain structure of [011]-oriented K_0.5Na_0.5NbO₃ crystal, grown by the floating zone method, by means of three complementary techniques: SEM, TEM and PFM. Then, we studied the lattice structure across the domain wall of K_0.5Na_0.5NbO₃ crystals using HRTEM. Finally, the piezoelectric properties of the [011]-oriented K_0.5Na_0.5NbO₃ crystal are reported and compared to those of a spark plasma sintered K_0.5Na_0.5NbO₃ ceramic.

Experimental details

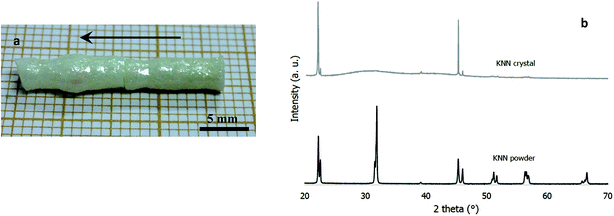
K_0.5Na_0.5NbO₃ (abbreviated KNN) crystals are grown using the floating zone method (FZM): the detailed route is described in ref. 28. A KNN crystal ingot of 40 mm in length and 5–6 mm diameter is obtained. An extracted sample from the KNN crystal ingot is shown in Fig. 1(a). Fig. 1(b) shows the X-ray diffraction pattern of the crystal sliced perpendicularly to the growth direction at 35 mm from the seed base. As the powder, the crystal exhibits an orthorhombic structure without secondary phase and have [011] preferential crystallographic orientation.

Fig. 1 (a) KNN sample extracted from crystal growth using floating zone method (FZM). The arrow represents the growth direction and (b) X-ray diffraction patterns of the KNN powder and the crystal sliced at 35 mm from the seed base.

The microstructure and domain structures observations are carried out using three complementary techniques:

SEM microstructural observation is conducted on a scanning electron microscope (SEM-FEI Quanta 200), operating at 20 kV, using backscattered imaging mode. To prepare the SEM sample, the surfaces of the sliced crystals are polished with SiC papers to about 100 μm thick and finally polished to a 1/4 μm finish with diamond suspension.

Transmission electron microscopy observations is performed at room temperature on a 200 kV JEOL 2010 FEG electron microscope (tilt ± 42°) and fitted with double tilt sample holder. For TEM observations cross sections of the KNN sliced crystals are prepared using an Ar ion beam provided by a JEOL Ion Slicer.

Piezo force microscopy and Kelvin probe force microscopy (KPFM) measurements are carried out at room temperature in air using a Solver, NT-MDT microscope and a silicon cantilever with Co/Cr-coating (resonance frequency ∼ 75 kHz, force constant ∼ 3 N m⁻¹). The sample preparation for both PFM and KPFM investigations is the same as the one used for the SEM study. The sample is electrically grounded by fixing it to the metallic substrate with conductive silver paste. For PFM measurements, an AC voltage V_AC = 1 V is applied to the cantilever to read PFM response. For KNN crystal, contact resonance frequency peak has been determined at 433 kHz and the selected modulation frequency is chosen to be 150 kHz. To switch polarization, a bias V_DC = ±10 V is used. To check the charge distribution before and after polarization modification, a two paths KPFM method with a contact potential difference (CPD) compensation is used. During the first path, morphology of KNN crystal is determined by tapping AFM mode. During the second path (i.e. lifted off = 8 nm), V_CPD = −0.17 V, electric field amplitude V_AC = 0.2 V with modulation frequency = 76 kHz are applied in order to measure the crystal surface potential. It must be noticed that this method just allows to image heterogeneous charge distribution at the surface. The d_eff33 = A/QV_ac, where A is the amplitude of the sample piezoresponse, Q is the quality factor and V_ac is the AC voltage is determined using PFM.

For electric and piezoelectric measurements, the crystal ingots of KNN which have cylindrical form are cut perpendicularly to the growth direction into discs of circa 5 mm diameter. The discs are polished to be 0.5 mm thick in order to obtain the thickness mode and painted with silver conductive paste (SPI. Supplies) on both sides. The disc is poled at 100 °C in silicone oil at 3 kV mm⁻¹ for 10 min using a DC power supply and cooled to room temperature by maintaining the electric field. For functional characterization, the KLM scheme²⁹ which is an equivalent electric circuit for thickness-expander plate, was used. This circuit is composed of electric and mechanical (corresponding to an acoustic line transmission) parts, separated by electromechanical transformer (symbolizing the piezoelectric effect). It allows to calculate the electric input impedance for an arbitrary acoustic load and vice versa. The advantage of this circuit is that it may be modeled into a series of quadrupoles which is characterized by a transfer function each one and allow to calculate the electromechanical properties. The detailed procedure used for the investigation of electromechanical properties is reported in ref. 6.

Results and discussions

Fig. 2(a) shows the SEM image of the domain structure obtained for [011]-oriented KNN crystals. The topographical features on the polished surface can be clearly identified and stripe-like microdomains are evidenced (6–7 μm wide). After chemical etching, a sub-domain configuration consisting of parallel stripes (1–4 μm wide) can be seen inside the dark and light zones (see the inset image). These parallel stripes are separated by 90° domain walls. Such domain structures might appear because of twin phenomenon in this orthorhombic structure or under the effect of composition modulation due to the presence of ordered vacancies because of the alkali volatilization at high temperature during crystal growth. In order to check this last point, EDS measurements have been done across the crystal in order to determine the amount of each element. Fig. 2(b) shows the composition distribution across the parallel domains (dark and light zones). Every point on the graph corresponds to an average value of 10 measurement points inside one parallel domain. The composition variations between two nearest parallel domains (dark and light zones) are quantitatively not significant. The average value of the cationic ratio (K + Na)/Nb is found to be 0.90. The composition of the crystal is within the stoichiometry with a slight deviation due to the alkali losses and the corresponding oxygen vacancies, taking into account the EDS experimental error, especially high on sodium element (∼5%).

Fig. 2 (a) Domain structure of the KNN crystal observed by scanning electron microscope. The inset image shows the domain structure after chemical etching. (b) Composition analysis measured by EDS across the parallel domains (see white arrow).

The KNN crystal cross section is examined using TEM. As shown in Fig. 3(a) and (b), different networks of parallel stripe-like microdomains with width in the range 0.4–1.5 μm are evidenced. Interestingly, zigzag sub-microdomains forming 90 and 120° orientations can be seen within the microdomains, as encircled in Fig. 3(a) and (b). These observed parallel stripe-like microdomains confirmed the organization of the ones already observed with SEM at a lower scale. These domain structures can be related to stresses developed in the crystal due to the crystallographic phase transitions undergone by KNN during crystal growth and cooling. It is well known that such kind of tetragonal to orthorhombic phase transition leads to the formation of twin structures in non-ferroelectric perovskites in order to minimize local stresses.^30,31 In KNN, the orthorhombic–tetragonal (O–T) polymorphic phase transition could lead to stresses located mainly in the (a and b) planes, which may induce twin domains formation due to energy minimizing, along 〈110〉 family directions in the orthorhombic phase. As reported by some authors, KNN crystals display such domain structures that completely disappear at ∼405 °C.³² Note with interest that the KNN material becomes also paraelectric at this temperature, corresponding to tetragonal–cubic transition, which implies the disappearance of the ferroelectric domains. This makes it difficult to distinguish these two effects and SEM/TEM microstructural figures might be attributed to stress accommodation (twin domains, antiphase boundaries) and/or ferroelectric domains.

Fig. 3 (a and b) TEM images of the KNN cross section showing parallel stripe-like microdomains. Zigzag sub-microdomains forming 90 and 120° orientations are arranged inside the microdomains (white circles).

Referring to these issues, high resolution transmission electron microscopy investigations are undertaken at room temperature to obtain direct evidence of possible defects near the domain walls or twin wall identification, at room temperature. Fig. 4(a) and (b) show the lattice images of KNN near a domain boundary. First of all, these observations attest, as expected, that KNN crystal in each domain displays good crystallinity without stacking defects (Fig. 4(a)) even at atomic scale (Fig. 4(b)). The EDS analysis in TEM is in good agreement with the SEM-EDS analysis. The main microstructural feature is that no disorder and no structural change identifying twin structure and no composition fluctuation are detected on either side of the domain wall.

Fig. 4 (a and b) High-resolution TEM images of the domain wall structure showing two neighbouring domains: white arrows represent the domain wall. (c) In inset Fast Fourier Transform (FFT) performed respectively right (1) and left (2) from the domain wall. The crystallographic orientation is more or less the same and each dots in the FFT are unique and not splitted. (d) FFT performed on the hole image on both domains (3) splitted dots are clearly evidenced (see enlargements in inset) on this FFT attesting of a small disorientation (less than 1°) between the two domains on each side of the wall.

The boundary (white arrows in Fig. 4(a)–(c)) is probably due to small misfits between the parameters and crystallographic direction changes of the different structures that can take place in the sample. Fast Fourier Transforms (FFT), performed on both sides of the domain wall, presented on Fig. 4(c) evidences that no changes are observed in the main crystallographic direction on either side of the domain wall. Even if these main crystallographic directions are maintained, Fig. 4(c) and (d) evidence the very small disorientations (less than 1°) observed on both sides of the wall. On the FFT, Fig. 4(d), splitted spots (insets Fig. 4(d)) attests of these phenomena. However, due to the size of the domains and the resolution of the data obtained from the FFT no conclusion can be made, on the basis of TEM observations, on the different cell parameter possibilities that could be observed in these samples.

The domain structures observed all over the sample can be attributed to the presence of regular antiphase boundaries generated by growth stresses relaxation or even polymorphic phase transition accommodation. The stripes observed with SEM may also correspond to these phenomena at a higher scale. The question arising now is the possible link between these antiphase boundaries and the ferroelectric domains. For that purpose, PFM studies on KNN crystals were performed to investigate its local ferroelectric domain structures and local polarization switching.

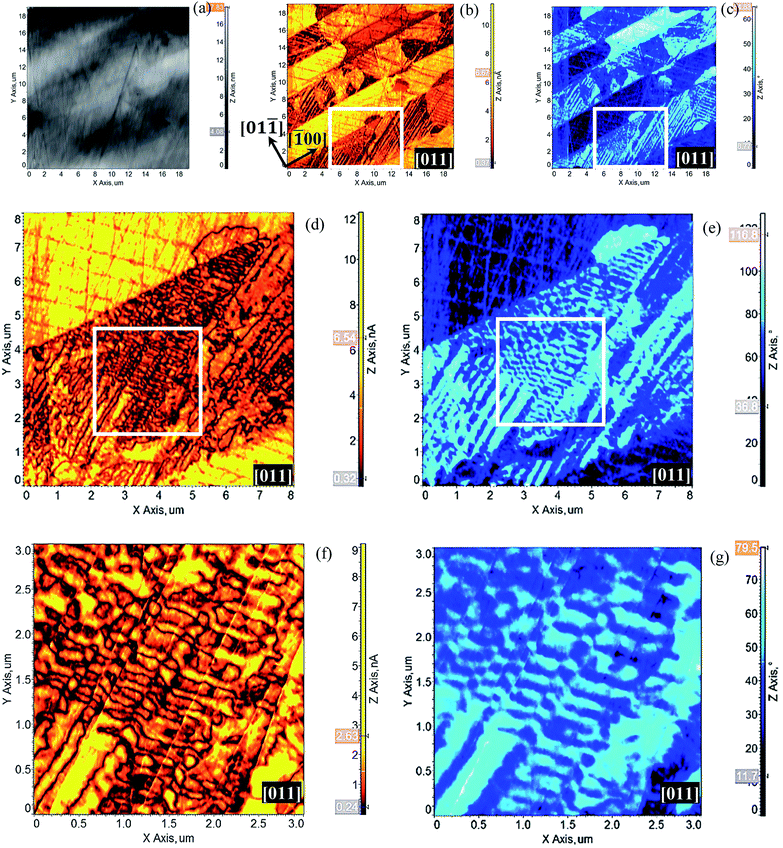
Topography of the polished surface of the KNN crystal with PFM images (amplitude and phase for OUT-plane component of piezoresponse) are shown on Fig. 5(a)–(c). Observed contrasts on PFM images confirm the piezoelectric response of the crystal. Parallel stripe-like microdomains oriented along the [001̄] crystallographic direction can clearly be seen (Fig. 5(b)-amplitude (domain walls), (c)-phase (polarization orientation)). The domain width is around 3–4 μm. Dark and bright regions on the phase image (Fig. 5(c)) correspond to upward and downward orientation of the OUT-plane component of polarization, respectively. Stripe-like microdomains structure confirms the one already observed by SEM and TEM (Fig. 2(a) and 3). PFM magnified images (Fig. 5(d)–(g)) show microdomains which contain sub-microdomains. One can clearly see that those sub-microdomains have different geometrical configurations: parallel stripes and zigzag. The first ones are located along [1̄11̄] crystallographic direction with width around 200–400 nm (Fig. 5(f) and (g)). Zigzag ones with width around 50–100 nm are oriented, in the image plane, at 90°, 180°, 60° and 120° to each other (Fig. 5(f) and (g)).

Fig. 5 (a) Morphology, OUT-plane component of the polarization: (b) amplitude and (c) phase (dark and bright regions correspond to up- and downward polarization, respectively). (d and e) Domains configuration in stripe-like microdomains. (f–g) Domains configuration of sub-microdomains.

Observed sub-microdomains (stripes and zigzag) have also been previously evidenced by TEM (Fig. 3(a) and (b)). Correlation in between PFM and TEM results confirms the accuracy between these techniques. It should be noticed that observed piezoresponses of micro- and sub-microdomains are not the same maybe due to different orientations of the OUT-plane polarization component which can strongly modify cantilever/crystal surface interactions.

In order to clearly identify ferroelectric domains, the reversibility of the local polarization switching is investigated. The bias to modify the polarization has been determined to be ±10 V which corresponds to an electric field value of 10⁴ V m⁻¹. It can be noticed that this value is very low in comparison with ones used for thin films (around 10⁸ V m⁻¹). It must be due to weaker constrains in single crystal.

So, for “writing”, a 3 × 3 μm² area is scanned in a contact mode with DC voltage V_DC = −10 V (applied to the cantilever). For “rewriting”, a 1.8 × 1.8 μm² area inside the previous one is selected and scanned with V_DC = +10 V. On obtained PFM images (amplitude and phase), one can clearly see “written–rewritten” regions, as shown in Fig. 6(a) and (b). Initial domain configuration is totally recovered (even sub-microdomains) after “rewriting” confirming the absence of pinning effect and, then, the high quality of the crystal. Despite this, we are not able to measure a difference of phase equal to 180° between domains exhibiting opposite polarizations. In order to check if it's an electrostatic effect we focused on KPFM measurements.

Fig. 6 Local polarization switching: (a) PFM amplitude, (b) PFM phase and (c) surface potential distribution.

For the same “written–rewritten” regions, the distribution of the surface potential (Fig. 6(c)) is determined. Different charge states corresponding to charge dynamics which appear during polarization switching were observed. But, the asymmetry of surface potential (from −120 to +340 mV) clearly shows that other effects happened during this “writing–rewriting” process. This observed surface potential distribution could have been implemented by the presence of screen charges or an electrochemical reaction in between cantilever and crystal surface.

These observations and measurements demonstrated that the antiphase boundaries caused by the growth stresses relaxation or even polymorphic phase transition accommodation during crystal growth and cooling are correlated with the formation and the organization of the ferroelectric domains.

Let us consider now the stripe-like domains contribution to the electromechanical properties of the (011) KNN crystal grown by the floating zone method. Fig. 7 shows, as example, a fit of the KNN electric impedance around the fundamental resonance. Table 1 summarizes the electromechanical properties of the crystal and for comparison, the results obtained with a spark plasma sintered KNN ceramic and a [011]-oriented KNNT-2 (Ta-doped) crystal obtained by another group with a different technique are added. The (011) KNN crystal displays k_t of 0.47 comparable to that of spark plasma sintered KNN ceramic. The KNN crystal exhibits piezoelectric coefficient d₃₃ around 60–80 pC N⁻¹ and clamped dielectric constant ε^S_r,33 (measured at 2f_a ∼ 12 MHz) of 123 which are two times smaller than those of the ceramic (d₃₃ of 127 pC N⁻¹ and ε^S_r,33 of 229). It is worth noting that the d₃₃ measured with a piezometer for the KNN crystal is 65 ± 5 pC N⁻¹, which is correlated to our measurements by using PFM. These differences are ascribed to the anisotropy of the crystal properties. Indeed, the orthorhombic crystal is oriented along the polar axis i.e. [011] and in this configuration the single domain state is unstable because of high elastic energy that is associated to 90° domains.³³ After removing the electric field, the [011]-oriented KNN crystal would partially depolarize, explaining why we obtained such properties. Further, KNN crystal presents dielectric losses of 0.07 and high mechanical losses of 0.21 compared to the ceramic. Gerthsen et al.³⁴ established both theoretically and experimentally that the dielectric and mechanical losses are induced by the vibrations of 90° domain walls under the influence of electric field. Hence, as observed in this work the presence of 90° domain walls in [011]-oriented KNN crystal might be the origin of the high mechanical losses. Besides that, our crystal presents superior properties of k_t and d₃₃ compared to those of [011]-oriented KNNT-2 (Ta doped crystal) grown by the top-seeded solution growth (TSSG). However, KNNT-2 crystal exhibits a slightly higher clamped dielectric constant of 181 than that of 123 in the undoped KNN crystal. Our electromechanical properties may be explained by the presence of parallel stripe-like sub-microdomains and zigzag nanodomains (see Fig. 5) in KNN crystal. Indeed, these fine domains could response easily to an external electric field, as confirmed by the local polarization switching test with PFM (see Fig. 6), which should improve the piezoelectric properties.

Fig. 7 Real and imaginary parts of the complex electric impedance of KNN crystal grown by the FZM (black solid lines: modeling and gray dotted lines: experimental data).

Table 1 Piezoelectric properties of (011) KNN crystal and ceramic. SPS: Spark Plasma Sintering; FZM: floating zone method; TSSG: top-seeded solution growth; k_t: thickness coupling factor; d₃₃: piezoelectric coefficient; ε^S_r,33: clamped dielectric constant δ_e and δ_m: dielectric and mechanical losses, respectively. For comparison, the properties of a [011]-oriented KNNT-2 crystal grown by TSSG are added. The d₃₃ = 65 pC N⁻¹ was measured with a piezometer (Piezotest PM300)

Composition	Method	kt	d33 (pC N^−1)	ε^Sr,33	δe	δm	Ref.
KNN (ceramic)	SPS	0.45	127 ± 5	229	0.003	0.02	6
[011]-KNN	FZM	0.47	60–80 pm V^−1, 65 ± 5	123	0.07	0.21	This work
[011]-KNNT-2	TSSG	0.365	56.2	181	—	—	33

---

Otherwise, in the literature, [001] oriented KNN crystals exhibit d₃₃ ranging from 148 to 160 pC N⁻¹ and dielectric constant (ε_r measured at ∼kHz) of 226–240.^32,35 Our [011]-oriented KNN crystal displays inferior properties than those oriented along the [001] direction, and as previously discussed, this difference is ascribed to the anisotropy of properties in piezoelectric crystals. Indeed, it is well established that the orthorhombic crystal oriented along the polar [011] direction displays inferior properties compared to that oriented along the non-polar [001] direction. This is due to the high instability of the single domain state that would partially depolarizes after removing the electric field after poling because of the high elastic and electrostatic energies associated to 90° and 180° ferroelectric domains, respectively.³³

Conclusions

In this study, hierarchical domains with different sizes are evidenced thanks to different techniques (SEM, TEM and PFM) in KNN single crystal grown by the floating zone method. The SEM observation showed long parallel stripe-like microdomains (6–7 μm in width), containing themselves a substructure consisting of parallel stripes (1–4 μm in width), the latter being also observed by TEM. Interestingly, inside the stripe-like microdomains a sub-structure consisting of zigzag sub-microdomains forming 90 and 120° domain walls is arranged. Moreover, high resolution TEM investigations showed the presence of regular antiphase boundaries that derived from the small misfits between the parameters of the average structures, forming thus the domain walls, which is directly correlated with the formation of stripe-like domains and sub-domains. More, no structural change and composition segregation are detected on either side of the domain walls, excluding twin boundaries formation.

From the properties point of view, PFM studies confirmed the piezoelectric response of the crystal and showed parallel stripe-like microdomains of 3–4 μm, containing sub-microdomains as well. These sub-microdomains are consisting of parallel stripes of 200–400 nm and zigzag nanodomains oriented at 60, 90, 120 and 180° to each other. Besides that, the local polarization switching test by PFM confirmed the ferroelectricity of KNN. The sub-microdomains (stripes and zigzag) observed with TEM and PFM allowed the correlation and accuracy between these two techniques to be confirmed. Moreover, the organization of the stripe-like domains from micrometer to nanometer scale evidenced the ferroelectric domains hierarchy in [011]-oriented KNN crystal, and can explain some aspects of the piezoelectric properties.

In summary, this study has shown that the internal stresses generated during crystal growth, due to the thermal gradient and cooling rates combined with structural transitions in KNN crystal grown by floating zone method, directly influence the large and fine structures of the ferroelectric domains, and thus the electromechanical properties.

Author contributions statement

M. Bah carried out material synthesis, crystal growth, sample preparation, SEM investigations, EDS analysis, electromechanical characterization and managed the project direction. N. Alyabyeva and A. Ruyter carried out PFM studies and assisted with interpretation of PFM data and co-writing of the paper. R. Retoux led all TEM investigations of K_0.5Na_0.5NbO₃ single crystals and co-wrote the paper. M. Zaghrioui, F. Delorme, F. Giovannelli and I. Monot-Laffez assisted with discussions and interpretations of SEM and TEM data and co-wrote the paper.

Acknowledgements

The authors wish to thank Muriel Strebel and Xavier Larose from CRISMAT Laboratory, CAEN (France) for samples preparation prior to TEM observations.

References

1. H. Deng, X. Zhao, H. Zhang, C. Chen, X. Li, D. Lin, B. Ren, J. Jiao and H. Luo, CrystEngComm, 2014, 16, 2760–2765.
2. Y. Saito, H. Takao, T. Tani, T. Nonoyama, K. Takatori, T. Homma, T. Nagaya and M. Nakamura, Nature, 2004, 432, 84–87.
3. M. Bah, F. Giovannelli, F. Schoenstein, C. Brosseau, J.-R. Deschamps, F. Dorvaux, L. Haumesser, E. Le Clezio and I. Monot-Laffez, Ultrasonics, 2015, 63, 23–30.
4. J. Rödel, K. G. Webber, R. Dittmer, W. Jo, M. Kimura and D. Damjanovic, J. Eur. Ceram. Soc., 2015, 35, 1659–1681.
5. J. Wu, D. Xiao and J. Zhu, Chem. Rev., 2015, 115, 2559–2595.
6. M. Bah, F. Giovannelli, F. Schoenstein, G. Feuillard, E. Le Clezio and I. Monot-Laffez, Adv. Appl. Ceram., 2015, 114, 211–219.
7. R. E. Jaeger and L. Egerton, J. Am. Ceram. Soc., 1962, 45, 209–213.
8. J. Fu, R. Zuo, D. Lv, Y. Liu and Y. Wu, J. Mater. Sci.: Mater. Electron., 2010, 21, 241–245.
9. X. Chao, Z. Yang, Z. Li and Y. Li, J. Alloys Compd., 2012, 518, 1–5.
10. Y. Chang, S. F. Poterala, Z. Yang, S. Trolier-Mckinstry and G. L. Messing, Appl. Phys. Lett., 2009, 95, 232905.
11. J. Fu, R. Zuo and Z. Xu, Appl. Phys. Lett., 2011, 99, 062901.
12. J. Yao, Y. Yang, N. Monsegue, Y. Li, J. Li, Q. Zhang, W. Ge, H. Luo and D. Viehland, Appl. Phys. Lett., 2011, 98, 132903.
13. J. Gao, D. Xue, Y. Wang, D. Wang, L. Zhang, H. Wu, S. Guo, H. Bao, C. Zhou, W. Liu, S. Hou, G. Xiao and X. Ren, Appl. Phys. Lett., 2011, 99, 092901.
14. M. Iwata, K. Ando, M. Maeda and Y. Ishibashi, Jpn. J. Appl. Phys., 2015, 54, 021502.
15. Z.-G. Ye and M. Dong, J. Appl. Phys., 2000, 87, 2312–2319.
16. L. Zheng, J. Wang, X. Huo, R. Wang, S. Sang, S. Li, P. Zheng and W. Cao, J. Appl. Phys., 2014, 116, 044105.
17. R. Lopez-Juarez, O. Novelo-Peralta, F. Gonzalez-Garcia, F. Rubio-Marcos and M.-E. Villafuerte-Castrejon, J. Eur. Ceram. Soc., 2011, 31, 1861–1864.
18. F. Rubio-Marcus, A. Del Campo, R. Lopez-Juarez, J. J. Romero and J. F. Fernandez, J. Mater. Chem., 2012, 22, 9714–9720.
19. Y. Huan, X. Wang, Z. Shen, J. Kim, H. Zhou and L. Li, J. Am. Ceram. Soc., 2014, 97, 700–703.
20. R.-P. Herber, G. A. Schneider, S. Wagner and M. J. Hoffman, Appl. Phys. Lett., 2007, 252905.
21. F.-Z. Yao, Q. Yu, K. Wang, Q. Li and J.-F. Li, RSC Adv., 2014, 4, 20062–20068.
22. K. Chen, G. Xu, D. Yang, X. Wang and J. Li, J. Appl. Phys., 2007, 101, 044103.
23. Y. Inagaki, K.-I. Kakimoto and I. Kagomiya, J. Am. Ceram. Soc., 2010, 93, 4061–4065.
24. D. Lin, Z. Li, S. Zhang, Z. Xu and X. Yao, J. Am. Ceram. Soc., 2010, 93, 941–944.
25. M. A. Rafiq, M. E. V. Costa and P. M. Vilarinho, Sci. Adv. Mater., 2014, 6, 426–433.
26. J. Yao, W. Ge, L. Yan, W. T. Reynolds, J. Li, D. Viehland, D. A. Kiselev, A. L. Kholkin, Q. Zhang and H. Luo, J. Appl. Phys., 2012, 111, 064109.
27. J. L. Peng and L. A. Bursill, Philos. Mag. A, 1983, 48, 251–263.
28. M. Bah, F. Giovannelli, R. Retoux, J. Bustillo, E. Le Clezio and I. Monot-Laffez, Cryst. Growth Des., 2016, 16, 315–324.
29. R. Krimholtz, D. A. Leedom and G. L. Matthaei, Electron. Lett., 1970, 6, 398–399.
30. G. Van Tendelo, H. W. Zandbergen and S. Amelinckx, Solid State Commun., 1987, 63, 603–606.
31. F. Delorme, I. Monot-Laffez, C. Harnois and G. Desgardin, EPJ Appl. Phys., 2001, 14, 159–163.
32. D. Lin, Z. Li, S. Zhang, Z. Xu and X. Yao, Solid State Commun., 2009, 149, 1646–1649.
33. L. Zheng, S. Li, S. Sang, J. Wang, X. Huo, R. Wang, Z. Yuan and W. Cao, Appl. Phys. Lett., 2014, 105, 212902.
34. P. Gerthsen, K. H. Härdtl and N. A. Schmidt, J. Appl. Phys., 1980, 51, 1131–1134.
35. S. Gupta and S. Priya, Appl. Phys. Lett., 2011, 98, 242906.

---