Ionic liquid prolongs DNA translocation through graphene nanopores

Abstract

The Lab-on-a-chip technology based on electrophoresis via nanopores is advancing at a fast pace to achieve low cost, fast, and reliable genomic sequencing. However, such a promising technique for genome sequencing is challenged by the uncontrolled faster DNA translocation speed and low signal to noise ratio. In this study, we have performed all-atom molecular dynamics simulations to investigate the effect of ionic liquid BMIM-Cl on dsDNA translocation through a nanopore grafted in a single layer of graphene. The presence of BMIM-Cl enhances DNA translocation time compared to the conventional KCl electrolyte solution. The study is capable of capturing the decelerating effect caused by ionic liquids. However, such a system has reduced ionic currents due to the low mobility of BMIM-Cl. The open pore current study demonstrated a pronounced effect of access resistance in such systems.

---

Introduction

The detection of DNA molecules at single base resolution by employing nanopore-based technology has paved the way for high throughput, label-free and low-cost personalized genome sequencing techniques. The method is based on a simple principle of measuring the reduction in ionic current while DNA passes through a nanopore under the influence of an external voltage. The increasing number of attempts to initiate a practical application of the nanopore-based technique for genome sequencing has not reached the National Human Genome Research Institute's (NHGRI) proposed target price of $1000 (ref. 1) due to various factors.

Biological pores like α-hemolysin, Mycobacteria smegmatis porin A (MspA), as well as solid-state nanopores have proved to be suitable materials for translocation studies with their intrinsic advantages and disadvantages.² The application of biological pores is limited due to low mechanical strength and pronounced sensitivity towards pH, temperature, and salt concentration. Nanopores grafted in solid-state materials such as single-layer graphene, MoS₂, or hafnium oxide are observed to be efficient alternative materials to biological nanopores. Solid-state nanopores allow calculation of the tunneling current as well as the ionic blockade current and provide higher accuracy in achieving single base detection.

During a translocation experiment, DNA is divided into fragments of ∼50 000 base pairs and passed repeatedly through nanopores to improve the single base reading. Under the influence of a voltage of the order of 10⁻³ volts, the translocation speed is approximately 2 μs per base. The generation of pico-ampere level ionic currents requires a high bandwidth amplifier for detection and is associated with high magnitude pink noise in graphene nanopores. Thus, DNA sequencing using solid-state nanopores is still challenged by fast translocation speeds and leads to large errors in single base detection of a DNA sequence.

The DNA translocation speed depends on various factors such as diameter of the nanopore (d), temperature, viscosity of the solution, applied electric field, pressure, and interaction of DNA with electrolyte ions. The relationship between the viscosity of a solution (η) and DNA translocation^3,4 speed (ν) is given by,

where ε is the dielectric constant of the electrolyte. ζ_d and ζ_w are zeta potentials of DNA and nanopore surface, respectively. E is the applied electric field. Hence, DNA translocation speed can be reduced (a) by increasing the viscosity of the electrolyte, (b) by applying low electric fields or (c) by reducing the zeta potential difference between the DNA and the nanopore (ζ_d − ζ_w).

Fologea et al.⁵ used glycerol–water solutions to slow down DNA translocation through solid-state silicon nitride nanopores. The study suggested that combined use of reduced temperature, a low bias voltage, and a high glycerol–water (50%) ratio would effectively slow down the DNA translocation speed. The same study indicated that there exists an interplay between the dwell time (t_d) and the amplitude of blockade ionic current or current drop, when one attempts to modulate other parameters like temperature, viscosity, and salt concentration. The dwell time is the mean translocation time for which the open pore current gets reduced. Reduction in the translocation speed also reduces the ionic conductivity, leading to a decreased blockade signal.

The DNA molecule is recognized by both dwell time and current drop (ΔI_b). The current drop (ΔI_b) is related to the thickness of the nanopore (H), the solution conductivity (σ), the hydrodynamic radius of the translocating molecule (R_DNA) and the applied voltage as,

The dwell time depends on the viscosity of electrolyte as,

where η is the viscosity of the solution. λ and L_DNA are the linear charge density and the length of the DNA molecule, respectively. V is the applied voltage and K is a constant for complex possible conditions. The increased interaction between the nanopore surface and the DNA governs the translocation speed.⁶ The experimental and MD simulation study performed by Mirsaidov et al.⁷ showed that the DNA translocation speed can be reduced up to 1 bp/2 ms by using reduced pore diameter (∼2 nm) and by modulating voltage and salt concentration (<200 mV and 100 mM KCl). With such a reduced speed, enhanced base-pair discrimination between C-G and G-C base pairs was observed. Akahori and coworkers⁸ reduced the nanopore diameter to enhance graphene–ssDNA interactions, which reduced the translocation time per base by up to 1.4 μs.

Wanunu and coworkers⁹ have shown the effect of salt gradient on DNA translocation motions. The “funneling effect” exerted by a salt gradient displays increased current rates and improves translocation times. Molecular dynamics simulation studies¹⁰ also corroborated these effects and suggested that nanopore surface charges play an important role in the trapping and translocation of polymers like dsDNA.

A nanopore created by a high intensity electron beam using a transmission electron microscope (TEM) generally assumes a negative charge. The electric field bias is needed to maintain the electro-osmotic flow of ions near the pore surface. Crowding of ions near the pore reduces translocation speed.¹¹ Negatively charged surfaces create competition in hydrodynamic coupling between the electro-osmotic flow of ions and DNA motions,³ thus retarding DNA translocation through the nanopore. The simulation study¹² also revealed that the reversal of the DNA's electrophoretic motion is caused by the strong binding of large organic cations like spermine (+4) and spermidine (+3).

The translocation speed can also be reduced by lowering the temperature^5,13 or using small diameter nanopores and high pressures.^14,15 In a theoretical study of pressure driven translocation, it was shown that the current reversal happens only in the presence of trivalent or higher valency cations. Kowalczyk et al. used LiCl solution¹⁶ to reduce the DNA translocation speed. This study indicated that strong binding of Li⁺ ions in the minor groove, primarily with O4′ atoms as well as N3 (of cytosine and thymine) and O2 (adenine and guanine) atoms of bases, reduces DNA translocation.

The increased viscosity and strong DNA–ion interactions can also slow down DNA translocation. Recently, room temperature ionic liquid BMIM-Cl¹⁷ was used to retard DNA speed while translocating through a mutated α-hemolysin nanopore. Both short-lived (∼50–100 μs) and long-lived (∼msec) translocation events were observed, albeit with a decreased current. The low current was attributed to the lower conductivity of 1 M BMIM-Cl (49.9 mS cm⁻¹) compared to a 1 M NaCl solution (81.6 mS cm⁻¹).¹⁷ The study showed that there exists a strong interaction between BMIM cations and DNA, which hinders the DNA squeezing through the nanopore.

The thickness of a single layer graphene sheet is 0.34 nm, similar to the DNA base pair separation. This makes the single layer of graphene a suitable material to achieve single base resolution through ratcheting motions of DNA bases. However, the effective use of graphene nanopores is limited by low (<3) signal to noise ratio (SNR). Also, the sticking of DNA to the graphene surface and nanopores restricts its effective use.^18,19 Nowadays different materials like MOS₂ (ref. 20 and 21) and hafnium oxide²² are used to achieve enhanced SNR (>15). In the case of MOS₂, the hydrophilic–hydrophobic–hydrophilic (S/Mo/S) arrangement of atoms reduces the noise in the ionic current. Also, the problem of DNA sticking to the pore surface is absent in MOS₂ nanopores.^20,23 Recently, an ionic liquid (BMIM-PF₆) induced viscosity gradient was used with an MOS₂ nanopore to reduce translocation speed and achieved a high SNR (>10).²¹ HfO₂ membranes with nanopores of less than 2 nm have also proved to be effective materials for DNA translocation.²²

Modi and coworkers²⁴ studied the translocation behavior of BMIM-CL in biological nanopores. Attaining the right orientation of BMIM⁺ molecules near the nanopore's constriction region was observed to be the rate-limiting step in its translocation. This orientation of BMIM⁺ was speculated to be an important factor in slowing down antibiotic translocation.²⁴ The passage of room temperature ionic liquid (RTIL) bulky ions through the nanopore channel creates ionic clouds near the nanopore surface. This accumulation of bulky ions alters the effective electric field and affects the translocation of molecules.²⁵

The single base resolution efficiency of a single layered graphene nanopore is reported in the literature, but its application is still limited mainly by the fast translocation speed as well as by graphene attachment of DNA on the trans side (top panel of Fig. S2 in ESI†) during the translocation process. The prolonged dsDNA translocation in a mutated α-hemolysin nanopore was achieved¹⁷ using BMIM-Cl as an electrolyte. However, the possible application of ionic liquids to reduce translocation speed in solid-state nanopores like graphene was not demonstrated.

In the present study, we have investigated the possible role of BMIM-Cl in reducing DNA translocation speed through a single graphene layer. Various simulations were performed to explore the effect of nanopore diameter and voltage on the translocation behavior of several homo-nucleotide sequences dA₂₀, dC₂₀, dG₂₀ and dT₂₀. Comparisons are drawn with normal salts such as KCl for a d(ACGT)₅ sequence based system. The results indicate that single base resolution can be improved by using smaller nanopores at a lower voltage gradient in the presence of ionic liquids. The translocation time increases compared to KCl solutions. The increase in translocation time is due to the slow passage of a strong DNA–BMIM⁺ complex through smaller nanopores.

Simulation details

System setup

We designed five DNA sequences, each containing 20 base pairs, as dA₂₀, dC₂₀, dG₂₀, dT_20, and d(ACGT)₅. The length of the DNA ensures that there are two helical repeats. Canonical B-form structures of DNA for the above sequence were constructed using the NAB²⁶ module of Ambertools.²⁷ The CHARMM27 force field parameters were chosen to perform the simulation. An armchair graphene sheet of approximately 9.8 nm × 9.8 nm was created using Nanotube builder in VMD.²⁸ The atoms within the required radius from the center atom were removed to create the pore. The ionic liquid 1-butyl-3-methylimidazolium chloride (BMIM-Cl) was used as an electrolyte. The BMIM optimized geometry was obtained using hf/6-31G*. The parameters were derived from ref. 29. The potassium and chlorine parameters were chosen from CHARMM27 force field for ions. GROMACS 4.5.3 (ref. 30) version was used to perform simulations. Each DNA-ionic liquid system was solvated with CHARMM27 TIP3P³¹ water. Ions were added randomly to make a 1 M concentration for both BMIM-Cl and KCl solutions.

The interaction between DNA and graphene nanopores is a crucial parameter to achieve base specific recognition. Hence, the choice of nanopore size is critical, as the large diameter pores possess fewer interactions with translocating DNA sequences and small pores can completely stop the electro-osmotic flow of ions. Generally, a nanopore of radius 1.2 nm was used as it is close to the radius of a dsDNA in B-form. In the case of BMIM-Cl, however, it was observed that using such a small nanopore allowed only dsDNA to pass and not bulky molecules of BMIM⁺ ions (data not shown). This observation led us to choose a nanopore radius by considering the hydrodynamic radius of BMIM⁺ cations.

The hydrodynamic diameter of BMIM is 0.57 nm.³² We have considered two possibilities, assuming dsDNA to be a cylinder: (a) BMIM⁺ molecules binding preferentially to either major or minor groove sides of a DNA sequence (see Fig. S1(a) in ESI†) and (b) BMIM molecules binding to both grooves (see Fig. S1(b) in ESI†). In the first case, the equivalent diameter of the DNA and attached BMIM would be 2.57 nm, thus requiring a nanopore of 2.6 nm diameter. In the second case, the effective diameter would be 3.14 nm. Thus, the DNA translocation simulations were performed for nanopores with diameters of 2.6 (smaller nanopore) and 3.1 nm (bigger nanopore). For each nanopore, we performed the calculations at two different voltage gradients, 0.05 V nm⁻¹ (lower voltage gradient) and 0.10 V nm⁻¹ (higher voltage gradient). These simulations are listed in Table S1 in ESI.†

Open pore current simulations were performed to determine mean ionic current value and its fluctuations. This study was extended for a pore diameter of 2.6 nm at different voltages to observe the I–V relationship in the case of the BMIM-Cl based system. Also, the relationship between resistance and diameter of the nanopore was studied using various open pore simulations. These simulations were performed with different pore diameters (2.4 nm, 2.6 nm, 2.8 nm, 3.0 nm, 3.1 nm, 3.4 nm, 3.8 nm and 4.6 nm) at the higher voltage gradient (VG). These simulations were performed for 5 ns each.

The graphene sheet was aligned along the XY plane and the dsDNA was aligned along the Z-direction. Two terminal base pairs of DNA were inserted inside the pore to avoid unwarranted DNA diffusion in the solvent in search of a nanopore (see Fig. S2 in ESI†). The end of the graphene sheet was restrained. The graphene sheet was modeled as a continuous periodic molecule to avoid end effects. Periodic boundary conditions were applied along the XYZ directions. The final box size of the system was approximately 9.8 nm × 9.8 nm × 19.8 nm.

The Particle Mesh Ewald method³³ was used to calculate electrostatic interactions with a cut-off value of 1.3 nm. We took a 1.2 nm cut-off radius for van der Waals interactions. Bonds involving hydrogen atoms were constrained during simulation using the LINCS algorithm. We carried out 20 simulations with DNA that involved four homo-nucleotide sequences at different conditions and four other simulations using the hetero-nucleotide sequence d(ACGT)₅. Each system contains approximately 184 000 atoms. Each system was simulated three times, starting with a different initial velocity, to obtain the error estimate.

Equilibration and data collection

Each system was heated slowly up to 300 K followed by a 50 ps equilibration using a Berendsen barostat and thermostat.³⁴ The production runs were performed using an NVT ensemble and by implementing V-rescale³⁵ as a thermostat. A recent study showed that a V-rescale thermostat maintains the canonical ensemble and reduces ionic current fluctuations.³⁶ Apart from 20 simulations monitoring DNA translocation under various conditions, four open pore simulations were performed for nanopore diameters of 2.6 nm and 3.1 nm at both 0.05 and 0.10 V nm⁻¹. For the smaller nanopore, ten open pore simulations were performed at ten different voltages to confirm that the system obeys Ohm's law and to study the I–V relationship in ionic liquid-based solid-state nanopores.

Analysis

DNA–graphene COM movement. Since the graphene sheet is placed in the X–Y plane, movement of the DNA and its translocation were determined by the change in the Z component of the distance between the centers of mass of the DNA and the graphene sheet. The Z-component of the DNA movement (D_Z) is normalized by its value at t = 0 (D₀). We have calculated normalized movement (D_Z/D₀) in all cases.

Ionic blockade current. As the electric field was applied along the Z-direction, the time-dependent ionic current was calculated from the Z-component of ions using the following equation,³⁷where L_z is the box length along the Z-axis. Δt is the time lag, which depends on the electrolyte of the system. It was suggested that Δt should be chosen such that the signal to noise ratio would be larger than five.³⁸ q_i is the charge on the i-th atom. In the case of BMIM-Cl, all atoms of BMIM⁺ and Cl⁻ ions were considered to contribute to the ionic current. Similarly, for KCl solution based systems, current due to K⁺ and Cl⁻ were considered.

Radial distribution function. We studied the radial distribution function of cations (BMIM⁺ or K⁺) around the DNA phosphate groups. In the case of d(ACGT)₅, we also monitored the distribution of Cl⁻ ions.

Charge distribution calculations. The charge distribution due to cations and anions for DNA translocation simulations in KCl and BMIM-Cl systems was calculated. The charge distribution along the Z-axis was calculated by dividing the simulation box into 200 slices perpendicular to the Z-axis and using the g_potential program in GROMACS.³⁰ The number of charged atoms belonging to a particular slice provides the effective charge distribution caused by the applied electric field. This potential is averaged over the number of frames and plotted along the length of a box in the Z-direction.

Results and discussion

Open pore current analysis

Signal to noise ratio (SNR). The success of the nanopore sequencing technique depends on the slow translocation speed of DNA with a high signal to noise ratio (SNR) in blockade current measurement. The open pore current calculations provide an opportunity to understand the SNR and conductance behavior of a simulation system under study. These studies help reveal the effect of time lag on the SNR ratio and I–V curves of the system, specific to simulation parameters like force field, thermostat, and other factors. Hence the reliability of MD simulations in exploring DNA translocation can be ascertained from open pore current calculations. The ionic current due to the passage of BMIM-CL molecules through the graphene nanopores can be calculated using eqn (4). The ionic current calculations are sensitive to the time lag (Δt), the choice of which in turn dictates SNR. We have studied SNR dependence on Δt for BMIM-Cl based systems to find the appropriate value of Δt, so that SNR remains above five. We have estimated SNR using an open pore current, which is the current estimated in the absence of the DNA, containing only 1 M BMIM-CL solution and nanopores of a given size. Open pore simulations were performed for two different nanopore diameters, 2.6 nm and 3.1 nm, at two different voltages of 0.05 V nm⁻¹ and 0.10 V nm⁻¹. SNR was then calculated using eqn (5).

Fig. 1 suggests that the recommended SNR value (above 5) is observed at 4 GHz (equivalent to a 250 ps time lag). Hence, all further simulations to estimate currents in the case of BMIM-CL based systems were performed using Δt = 250 ps. This value is almost five times higher than the suggested value of 50 ps in case of KCl solutions.³⁶ The SNR is defined as,³⁹

here, I_avg is the average open pore ionic current and I_SD is a standard deviation of the ionic current when a particular Δt is used. The noise in spectral density of a signal is inversely proportional to the frequency (f) and has a stochastic origin; such noise is called 1/f noise. At high frequencies, 1/f noise is comparable to the magnitude of the signal and hence leads to poor detection. For a single conical nanopore, the use of ILs like BMIM-TFSI and EMIM-SCN provides better SNR, due to the crystal-like self-assembled structures.⁴⁰ The eventual slow dynamics of the translocation of ionic liquids exhibits jammed-like⁴¹ motions which enhances the SNR.⁴⁰ Hence, the use of an ionic liquid may help to enhance the SNR in solid-state nanopores.

Fig. 1 SNR for diameter (D) 2.6 nm at voltage gradients (VG) at (a) V = 0.05 V nm⁻¹ and (b) V = 0.10 V nm⁻¹.

Fig. 2 indicates that for the smaller nanopore, the average current values are 7.39 nA and 7.70 nA for the lower and higher voltage gradients, respectively. Similarly, the open pore current values for the bigger pore are 8.28 nA and 9.92 nA for the lower and higher voltage gradients, respectively. Fig. 1a and b indicate that the average current values remain almost same in both cases. The choice of Δt is independent of voltage applied to the above systems. Also, it indicates that one needs high frequency apparatus to detect currents of such low values, eventually increasing the chance of instrumental errors. Such errors can be reduced by using Al₂O₃ nanolaminated graphene membranes as shown previously.⁴² It has also been shown that nanopores with larger diameters have better SNR in low salt regions.³⁹

Fig. 2 Open pore current behavior for nanopores of diameter 2.6 nm at (a) 0.05 V nm⁻¹ and (b) 0.10 V nm⁻¹.

Variation of current against voltage. Since we used a non-conventional electrolyte, we wanted to verify whether BMIM-CL follows Ohm's laws using a voltage and current relationship. For this, we chose the smaller nanopore and performed simulations at ten different voltage gradients ranging from 0.01 to 0.20 V nm⁻¹. Each simulation was performed for 5 ns. The current was calculated in each case using eqn (4) for two different time lags (50 ps and 250 ps). The I–V plot (Fig. 3) shows a linear relationship between the voltage and current as expected from Ohm's law. However, it has a nonzero intercept on the ordinate. The simulation at 0 V, performed to check the values of ionic current and thermal fluctuations in the system, showed the presence of a 0.01 nA current. The open pore current and graphene pore conductance were calculated to determine the accuracy of the MD simulations. The open pore current study predicts a higher bulk conductivity for 1 M BMIM-Cl than the experimental bulk conductivity value as shown below. The bulk conductivity of the BMIM-Cl solution is calculated using the method implemented by Aksimentiev et al.³⁷ in their previous study. The slope of the I–V plot in Fig. 3 provides a direct measurement of the bulk conductivity. The bulk conductivity is found to be 67.1 S m⁻¹, which is higher than the experimental value of 4.62 S m⁻¹. The study by Modi et al.²⁴ also observed a slightly enhanced conductivity for BMIM-Cl using a TIP3P water model. Hence, the unusually high conductivity observed in this study may be attributed to the BMIM-Cl force field parameters and is partly due to the TIP3P water model.

Fig. 3 I–V characteristic of the system.

The accuracy of the electrochemical properties of IL depends on the force field of IL as well as on the water model. We would like to stress that the current IL force field model was chosen on the basis of its ability to present accurate DNA–IL interactions,⁴³ at the cost of losing accuracy in the electrochemical property. We believe that even though the bulk conductivity value is high, the qualitative trends in translocation will remain unchanged.

Behaviour of current. Fig. 2 shows open pore current fluctuations through the smaller nanopore at two different voltage gradients. Open pore current fluctuations are significant in both cases, possibly due to fluctuations in the effective unoccupied area of a nanopore by bulky BMIM ions, as demonstrated earlier.⁴⁴

Also, we can see a dip at around 2200 ps in the case of the lower voltage gradient (Fig. 2a). Hence, bulky molecules like BMIM⁺ can introduce a current blockade. The average current in both cases is similar – 7.39 nA for 0.05 V nm⁻¹ and 7.70 nA for 0.10 V nm⁻¹.

Resistance and pore diameter relationship. We have observed the dependence of resistance on the pore diameter, which was found to follow a nonlinear relationship. The nanopore size can affect the conductance of bulky BMIM⁺ cations due to electrostatic interactions⁴⁵ with the graphene surface leading to a different arrangement of cations near the graphene interface. The conductivity of ionic liquids depends strongly on the size of the ions and on pore diameter. Experimentally, low conductivity was observed in the case of pores having diameters less than 20 nm according to the hindered transport theory.^46,47 If the thickness of the electric double layer is comparable with the pore diameter, then ionic current rectification is observed. This rectification generates asymmetry in the I–V curve. The experimental⁴⁸ and previous theoretical study¹⁸ based on the KCl electrolyte observed that the resistance varies inversely with the square of the diameter of a nanopore.

Surprisingly, Fig. 4 shows that for a BMIM-Cl based system the data from the simulation fits well with Hall's equation for total resistance of a nanopore as shown below,⁴⁹

R = a₀/d² + a₁/d, (6)

where a₀ = 4L/πσ and a₁ = 1/σ, L is length of the nanopore, σ is the bulk conductivity of the BMIM-Cl solution, d is the diameter of nanopore. The calculated values obtained here are a₀ = 1976.41, a₁ = −292.17 with a correlation coefficient of 0.98 and χ² = 834.4. A good fit to eqn (6) indicates the presence of an enhanced nonlinear dependence of the resistance of the system on the pore diameter. The first term of eqn (6) represents the channel resistance and the second term of eqn (6) represents the access resistance. The access resistance arises from a resistance of the medium outside the nanopore and causes a significant reduction in potential near the pore mouth. The higher values of both a₀ and a₁ indicate that the channel resistance as well as access resistance significantly contribute to the total pore resistance.

Fig. 4 Dependence of resistance on the pore diameter.

The current study does not allow comment on the negative value of a₁. However, based on eqn (6), we would like to speculate on possible reasons for the negative value of coefficient a₁. First, we assume that the conductivity of a BMIM-Cl solution is different in the bulk solution (σ_channel) and near a graphene nanopore (σ_access). The negative conductivity for the access resistance can be assumed to be due to reversal of the current near the small region of the nanopore. At the microscopic level, some BMIM⁺ molecules might be dragged against the direction of the potential gradient due to strong binding with the DNA molecule. These bound BMIM⁺ cations may get stripped off near the nanopore surface while translocating, creating negative access resistance near the nanopore. However, we strongly believe that further study is required to verify this effect and to understand whether this phenomenon is only a local effect or an overall signature for these particular types of IL–nanopore systems.

Polynucleotide translocation time

The long DNA sequences threading through the small aperture are discriminated based on signature translocation time and ionic current blockades of individual bases. To understand the effect of IL on the DNA translocation, we have performed a series of simulations with different DNA base pairs, different sizes of nanopores and different voltage gradients. The translocation time values for individual runs are listed in Table S2 in ESI.†

The initial structure of a simulation contains the DNA partially inserted in the nanopore. Hence, the time required for a DNA sequence to completely pass through the pore may be considered to be the “translocation time” for the DNA. The translocation time is decided on the basis of the position of the center of mass (COM) along the Z-axis, also confirmed by visual inspection of trajectories. For the smaller nanopore at both voltage gradients, DNA sticks to the graphene surface after translocation on the trans side, causing partial blockades (see Fig. S3 in ESI†). In such cases, the translocation time is estimated when the last atom of DNA passes through the pore and no partial blockades are observed. The DNA COM movement projected on the Z-axis is normalized in Fig. S4 of ESI.† It helps to compare the behavior of the translocation time under different conditions, as the D₀ value for different sequences varies slightly due to inherent differences in COM of the sequences.

Previous studies^39,50 have shown that smaller nanopores and low electric fields enhance the interaction between solid-state nanopores and DNA, eventually providing better discrimination of the bases. Fig. 5 indicates that for the smaller nanopore at lower voltage gradient (VG) and, surprisingly, the bigger nanopore at higher VG, individual bases can be discriminated on the basis of the translocation time. The normalized DNA COM movement through the smaller nanopore at lower VG (see Fig. S4(a)†) indicates that all bases exhibit translocation times of more than 3000 ps. Such slow translocation is always affected by the strong DNA–graphene interactions, which eventually cause the DNA to stick to the nanopore surface. This effect is observed in Fig. S4(a) in ESI,† where D_Z/D₀ values converge beyond 2500 ps. This effect is absent in the larger nanopore of diameter 3.1 nm, where we can see a sharp COM movement indicating less interaction between the hydrophobic graphene surface and DNA. The steep slope of the curve of COM against time in the case of the large nanopore indicates a fast translocation process and hence less interaction with graphene. It is known that the DNA–graphene interaction affects DNA translocation speed.⁶ The normalized DNA COM movement through the larger nanopore at the lower VG shows the signature translocation velocities for each type of nucleotide. Hence, dA₂₀, dC₂₀, dG_20, and dT₂₀ show significantly different electrophoretic mobilities under this condition. The increased electric field enhances the electrophoretic force on DNA in a nano-channel. It was shown that current blockades are caused by reduction in ion mobility due to the strong interaction between DNA grooves and surface atoms.⁵¹ Also, the avalanche of BMIM⁺ cations moving in the opposite direction provides the desired sequence-dependent translocation time discrimination of the bases.

Fig. 5 Translocation time for (a) smaller nanopore (diameter 2.6 nm) at lower (0.05 V nm⁻¹) voltage gradient (VG); (b) smaller nanopore at higher (0.10 V nm⁻¹) VG; (c) bigger nanopore (diameter 3.1 nm) at lower VG; (d) bigger nanopore at higher VG.

The similar translocation time for all polynucleotides in the case of the smaller nanopore at high VG indicates the absence of distinctive DNA–graphene interactions due to fast translocation and hence it shows lower resolution for the blockade current. Hence, Fig. 5 suggests that effective parameters such as a pore diameter of either 2.6 nm or 3.1 nm can be implemented at 0.05 V nm⁻¹ and 0.10 V nm⁻¹ voltage gradients, respectively, to achieve translocation times that will distinguish between nucleotide types.

The normalized DNA COM behavior for the above-mentioned effective parameters is almost the same for dA₂₀ and dG₂₀ sequences. We assume that this behavior results from similar cross-sectional area of guanine (56 Ų) and adenine (50 Ų).⁵² Molecular dynamics studies showed that it is difficult to trace long-lived and short-lived signals for pore diameters of less than 3 nm.⁵³

The effective force on a charged polymer like DNA can be roughly estimated as q × E, where q is the effective charge on DNA and E is the applied electric field. Previous studies have shown that the reduction in the effective charge on DNA is caused by the hydrodynamic drag⁵⁴ of the electro-osmotic flow of ions. The electro-osmotic flow depends on the local concentration of ionic species as well as on the viscosity of the medium.

To consider the effect of these conditions on a heterogeneous sequence, we have studied the translocation of the d(ACGT)₅ sequence in 1 M KCl and 1 M BMIM-Cl solutions. Fig. 6 depicts the slowing down of DNA translocation in IL solution, prolonging the total translocation time. The effect is pronounced for the smaller pore. For the smaller pore, translocation in KCl solution was completed in around 1.5 ns, whereas the same sequence required approximately 3 ns to complete translocation in BMIM-Cl solution. This indicates a two-fold increase in translocation time in the case of a heterogeneous DNA sequence. The convergence in DNA COM movement after complete translocation is due to the adherence of the DNA on the trans side at a low VG of 0.05 V nm⁻¹. Even the larger nanopore shows the reduced DNA speed in the presence of the IL compared to salt solution. However, the difference is less significant.

Fig. 6 Center of mass (COM) displacement of ACGT system in BMIM-CL and KCl at 0.05 V nm⁻¹ for (a) diameter 2.6 nm and (b) diameter 3.1 nm.

The enhanced translocation time allows DNA molecules to interact strongly with the nanopore. This results in an increased number of blockade events and hence provides a better single base resolution. We have demonstrated an increase in blockade events by plotting the current for smaller and bigger nanopores at 0.05 V nm⁻¹ using a 50 ns lag for both the simulations (see Fig. S5 in ESI†). This analysis helps to compare the number of blockade events presented by frequent dips in the current values in the above cases. We can see in Fig. S5(a)† that the number of blockade events is considerably higher in the case of BMIM-Cl than for KCl, providing a better single base resolution.

Blockade current during polynucleotide translocation

Since the DNA is already partially inserted in the nanopore at the onset of the simulation, the current observed until the complete translocation can be considered to be the blockade current.

Fig. 7 shows the blockade current averaged over 3 simulations. The ionic current value for individual runs is listed in Table S3 in ESI.† The ionic blockade currents for the smaller nanopore at lower VG are less distinguishable for A₂₀, C₂₀, G₂₀ and T_20. Also, they are low as the blockade current is proportional to the applied voltage. At the higher VG, the difference in blockade current among the different nucleotides is insignificant. Hence, at the lower VG, individual nucleotides might be distinguishable using both translocation time and ionic blockade current. A major challenge to detecting significant ionic blockades, however, will remain, as the ionic currents in ILs are small compared to KCl or NaCl based electrolytes.

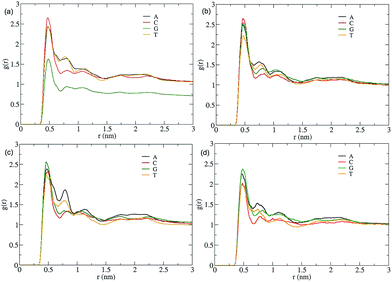
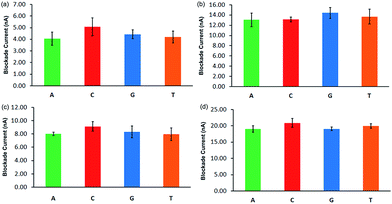Fig. 7 Ionic blockade current (calculated using eqn (4) with 250 ps time lag) for (a) smaller nanopore at lower VG; (b) smaller nanopore at higher VG; (c) bigger nanopore at lower VG; (d) bigger nanopore at higher VG. See Fig. 5 for other details.

It can be noticed that the blockade current value for the bigger nanopore is higher than for the smaller nanopore at the same voltage gradient, indicating an enhanced flow of electrolytes in the former. In the case of the bigger nanopore at lower VG (see Fig. 7c), the blockade currents are high and these values are comparatively more distinguishable. The adenine and cytosine have significantly different values, whereas thymine and guanine have almost the same blockade current. The presence of DNA in a nanopore reduces the effective cross sectional area of the pore and alters the local ion concentration near the pore. Both these factors cause an ionic current blockade.

Fig. S6† shows the ionic current fluctuations with time under different conditions. We can see the presence of shallow blockades in the translocation current for the smaller nanopore at low VG (Fig. S6(a)†), indicating brief halts of DNA during translocation. The ionic current blockade signatures for different nucleotides are sensitive to the orientation of the nucleotides passing through the nanopore.¹⁹ Hence, ionic current fluctuations are not the same for all three simulations (data not shown). We then carried out the translocation of the hetero-nucleotide sequence, d(ACGT)₅ using the smaller nanopore and lower VG (since the higher VG will result in faster translocation). For these hetero-nucleotide sequences, currents obtained for the IL electrolyte are less than for KCl for both nanopores at the smaller voltage gradient (see Fig. 8).

Fig. 8 The ionic current for d(ACGT)₅ system in BMIM-CL and KCl at 0.05 V nm⁻¹ for (a) smaller nanopore, and (b) bigger nanopore. The running average of ionic current for KCl systems is shown by the red line.

This behaviour can be directly correlated with the difference in conductivities of KCl and BMIM-Cl solutions. Experimentally, it is observed that current blockades are inversely proportional to the viscosity of solution. However, the present study is unable to capture the behaviour seen in Fig. 8.

The running average for KCl currents (red line in Fig. 8) is plotted to visually observe the trend in the currents. We can see that the ionic current blockades are prominent in the KCl based solution, contrary to the experimental observation. We attribute this discrepancy to the difference in the time lag used to calculate ionic currents. Computationally, the short time lag (50 ps) used for the KCl system to calculate the ionic current captures the fluctuations of the current, whereas in the case of BMIM-Cl, the bigger time lag of 250 ps averages out these fluctuations, indicating a lesser presence of blockade events. The translocation in the KCl system is completed within 2500 ps and yet Fig. 8a shows a fluctuation in current, possibly due to variation in the number of K⁺ and Cl⁻ ions. For a BMIM-Cl based system, however, a distribution of small blockade events is present until 4500 ps.

When simulations were performed for both systems using the bigger nanopore, the reduction in the number of translocation events was observed for both systems. Hence, we propose that even though the bigger nanopore can discriminate between nucleotides based on the translocation time, it will fail to achieve better resolution in the case of a heterogeneous sequence due to the reduction in translocation events.

Ion distribution around DNA

The anchored BMIM⁺ ions in DNA effectively increase its width and reduce the translocation speed of DNA. Hence, we have studied the radial distribution (RDF) of cations and anions around DNA. Note that the electric field is applied along the length of the DNA. Therefore, the RDF of ions around DNA should not be affected by the electric field.⁵⁵ BMIM⁺ ions were observed to accumulate strongly around negatively charged phosphate groups of DNA in a previous study.⁴³ These interactions are mainly electrostatic in nature. The study showed that BMIM-Cl has a binding free energy of ∼8.96 kcal mol⁻¹, indicating a strong binding with DNA.⁴³ It is suggested that BMIM binds strongly to the minor groove due to hydrogen bond interactions between the planar imidazolium ring and exocyclic moieties of nucleotide bases.⁴³ We have not considered the RDF around grooves as their width and depth change along the course of the translocation due to stretching of the DNA duplex. Fig. 9 shows the distribution of N1 atoms of the BMIM⁺ cation (Fig. S7 in ESI† for N1 atom) around the phosphate backbone of DNA under different conditions. We can see that in the case of the smaller nanopore at the lower VG, the ion distribution is different in each case. The distribution of BMIM⁺ is similar in the cases of dA₂₀ and dT₂₀. The highest number of ions is observed around dC₂₀ and lowest around dG₂₀. We see that even though dC₂₀ is strongly surrounded by bulky BMIM⁺ cations, it has the lowest translocation time but the highest blockade current under these conditions. This suggests that DNA–BMIM⁺ behaves as a combined complex during the translocation and hence it results in large current blockades. However, the number of attached BMIM⁺ ions is not sufficient to reduce the translocation speed of the DNA and hence dC₂₀ has a smaller translocation time. For the smaller nanopore, dC₂₀ is always surrounded by a large number of BMIM⁺ ions, whereas dG₂₀ is always surrounded by a larger number of BMIM⁺ ions for the bigger nanopore. This indicates that pore size affects the distribution around the DNA. The dA₂₀ sequence displays a significant second solvation shell under all four conditions, suggesting the presence of long-range interactions between BMIM⁺ and dA₂₀. Such strong interactions may increase the translocation time in almost all cases except for the bigger nanopore at the lower VG.

Fig. 9 Radial distribution function of N1 atom of BMIM⁺ around phosphorous atom of DNA for (a) smaller nanopore at lower VG; (b) smaller nanopore at higher VG; (c) bigger nanopore at lower VG; (d) bigger nanopore at higher VG.

We assume that if more BMIM⁺ cations are present close to a DNA sequence, then it will be difficult to strip them off as they interact strongly with the DNA via non-covalent interactions.

To understand this, we have studied the RDF for d(ACGT)₅ simulations carried out for the smaller nanopore at the lower VG. The RDF in Fig. 10 indicates that BMIM⁺ interacts strongly with the DNA and has a broader first layer of solvation compared to K⁺ ions in KCl solution. The effect of BMIM⁺ cations is long-range compared to that of K⁺ ions. This supports our hypothesis that removal of strongly bound BMIM⁺ ions from DNA increases translocation time. It is observed for BMIM-PF6 IL that a well ordered structure of IL exists near the uncharged graphite surface and that the first adsorption layer of BMIM⁺ is arranged parallel to the graphite surface up to a distance of 3.5 Å.⁵⁶ The enhanced RDF of BMIM⁺ ions can also be attributed to such structured arrangement. The RDFs of Cl⁻ ions in both cases display almost the same distribution and, hence, show a lower effect of the anion species on the translocation process.

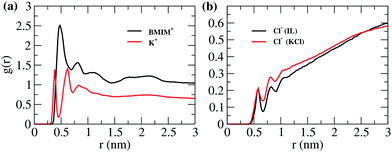Fig. 10 (a) Radial distribution function of N1 of BMIM and K⁺ around P of DNA for d(ACGT)5 and (b) radial distribution function of Cl⁻ around P of DNA for d(ACGT)5 in both cases IL and KCl.

Charge distribution along a nanopore

We have calculated the charge distribution of cations and anions along the Z-axis of the system. Fig. 11 shows the difference between the charge distribution of K⁺ and BMIM⁺ cations near the nanopore. It indicates that bulky BMIM⁺ ions accumulate near the nanopore, enhancing the effective positive charge near it. The strong electrostatic interactions between the negatively charged DNA backbone and accumulated positive BMIM⁺ ions reduce the translocation speed.

Fig. 11 Charge distribution along the Z-axis perpendicular to graphene surface for heteronucleotide DNA sequence d(ACGT)₅ in both BMIM-Cl and KCl systems.

This phenomenon is similar to the flow reversal at the interface of a silicon nano-channel due to immobilization of cations on the pore surface.⁵⁷ The charge reversal is not possible in the current case because of the short length of the nanopore. Luan et al.⁵⁵ observed that bulky cations like spermidine (+4) and spermidine (+3) induced reversal in electrophoretic mobility. This reversal was attributed to the strong interaction between these ions and the minor groove of DNA. It was suggested that electric charge inversion or a charge screening effect can be observed through the RDF distribution of ions.⁵⁵

Hence, we propose the presence of strong electrostatic attractions between DNA and well-structured BMIM⁺ ions near the graphene surface as the main driving force to reduce DNA translocation speed.

Conclusion

The current study is focused on different aspects of the translocation process, such as open pore current behaviour, the dependence of the resistance on the diameter of the nanopore, the individual blockade current as well as translocation time for polynucleotide sequences. The study was extended to understand the effect of BMIM-Cl on the translocation of a heteronucleotide sequence like d(ACGT)₅ compared to KCl solutions.

The open pore current study indicates a linear current–voltage relationship for a BMIM-Cl based system. A higher bulk conductivity is observed for a 1 M BMIM-Cl solution compared to the experimental value, which might be attributed to the combined effect of the simulation parameters for a BMIM⁺ cation in the presence of the TIP3P water model implemented in this study. We have also investigated the dependence of signal-to-noise ratio (SNR) for an IL-based system. The study suggests the need for high bandwidth amplifiers (of 250 GHz range) to maintain SNR >5 due to the low conductance of the BMIM-Cl solution.

A series of simulations with different nanopore diameters at a particular voltage gradient was performed to understand the dependence of the resistance of the system on pore diameter. The resistance exhibits nonlinear dependence on the diameter of the nanopore. In addition, the results indicate that total resistance depends on the contributions from both channel and access resistances.

To understand the discrimination capability between individual nucleobases, we have simulated the translocation of homo polynucleotides DNA sequences dA₂₀, dC₂₀, dG₂₀, and dT₂₀ in the presence of a 1 M BMIM-Cl ionic liquid solution. The simulations were performed at two different pore diameters, 2.6 nm and 3.1 nm. For each of them, two different voltage gradients (0.05 V nm⁻¹ and 0.10 V nm⁻¹) were used. The study suggests that the use of smaller nanopore and low VG can help to distinguish different nucleotides on the basis of translocation times in the presence of a BMIM⁺ ionic liquid. The blockade currents were less distinguishable for different bases under all conditions used. The electrophoretic mobility for different homo-nucleotide sequences was found to be different for the bigger nanopore at low VG (see Fig. S4(b)†). This suggests that bigger nanopore can also be used in the case of electrolytes of bigger cations like BMIM⁺.

To understand the difference between translocation mechanisms of common KCl solutions and BMIM-Cl solutions, we have compared the translocation of hetero-nucleotide sequence such as d(ACGT)₅ in both 1 M KCl and 1 M BMIM-Cl solutions. The results suggest that the presence of an enhanced positive charge near the nanopore (see Fig. 11) reduces the DNA translocation speed by strong interaction with DNA. The radial distribution function shows a preferential strong interaction between DNA and BMIM⁺ ions compared to K⁺ ions as the underlying mechanism for the reduced translocation time in IL.

This study also suggests that viscous BMIM-Cl or any other suitable ionic liquid can be utilized to reduce the DNA translocation speed. However, better resolution can be achieved using solid-state nanopores like MOS₂ or HfO_2, which have inherently high SNR. In addition, DNA soaked in ionic liquid in the cis chamber and KCl solutions in the trans chamber will provide better single base resolution in DNA sequencing, as shown by a recent study.²¹

Acknowledgements

Authors acknowledge Department of Science and Technology (SB/S1/PC-39/2012) for funding. M. K. thanks Indian Institute of Science Education and Research, Pune for fellowship. Authors thank Reman Kumar Singh, Debasis Saha, and Hridya V. M. for helpful discussions and suggestions during the preparation of the manuscript.

References

1. E. Porcu, S. Sanna, C. Fuchsberger and L. G. Fritsche, in Current Protocols in Human Genetics, John Wiley & Sons, Inc., 2013, vol. 78, ch. 1.25, pp. 1.25:21-21:25:14.
2. Y. Feng, Y. Zhang, C. Ying, D. Wang and C. Du, Genomics, Proteomics Bioinf., 2015, 13, 4–16.
3. S. Ghosal, Phys. Rev. Lett., 2007, 98, 238104.
4. D. Kejian, W. M. Sun, H. Y. Zhang, X. L. Peng and H. G. Hu, Appl. Phys. Lett., 2009, 94, 014101.
5. D. Fologea, J. Uplinger, B. Thomas, D. S. McNabb and J. L. Li, Nano Lett., 2005, 5, 1734–1737.
6. M. Wanunu, J. Sutin, B. McNally, A. Chow and A. Meller, Biophys. J., 2008, 95, 4716–4725.
7. U. Mirsaidov, J. Comer, V. Dimitrov, A. Aksimentiev and G. Timp, Nanotechnology, 2010, 21, 395501.
8. R. Akahori, T. Haga, T. Hatano, I. Yanagi, T. Ohura, H. Hamamura, T. Iwasaki, T. Yokoi and T. Anazawa, Nanotechnology, 2014, 25, 277501.
9. M. Wanunu, W. Morrison, Y. Rabin, A. Y. Grosberg and A. Meller, Nat. Nanotechnol., 2010, 5, 160–165.
10. Y. H. He, M. Tsutsui, R. H. Scheicher, C. Fan, M. Taniguchi and T. Kawai, Biophys. J., 2013, 105, 776–782.
11. Y. H. He, M. Tsutsui, C. Fan, M. Taniguchi and T. Kawai, ACS Nano, 2011, 5, 5509–5518.
12. B. Q. Luan and A. Aksimentiev, Soft Matter, 2010, 6, 243–246.
13. D. V. Verschueren, M. P. Jonsson and C. Dekker, Nanotechnology, 2015, 26, 234004.
14. B. Lu, D. P. Hoogerheide, Q. Zhao, H. Zhang, Z. Tang, D. Yu and J. A. Golovchenko, Nano Lett., 2013, 13, 3048–3052.
15. S. Buyukdagli, R. Blossey and T. Ala-Nissila, Phys. Rev. Lett., 2015, 114, 088303.
16. S. W. Kowalczyk, D. B. Wells, A. Aksimentiev and C. Dekker, Nano Lett., 2012, 12, 1038–1044.
17. R. S. S. de Zoysa, D. A. Jayawardhana, Q. T. Zhao, D. Q. Wang, D. W. Armstrong and X. Y. Guan, J. Phys. Chem. B, 2009, 113, 13332–13336.
18. C. Sathe, X. Q. Zou, J. P. Leburton and K. Schulten, ACS Nano, 2011, 5, 8842–8851.
19. D. B. Wells, M. Belkin, J. Comer and A. Aksimentiev, Nano Lett., 2012, 12, 4117–4123.
20. A. B. Farimani, K. Min and N. R. Aluru, ACS Nano, 2014, 8, 7914–7922.
21. J. Feng, K. Liu, R. D. Bulushev, S. Khlybov, D. Dumcenco, A. Kis and A. Radenovic, Nat. Nanotechnol., 2015, 10, 1070.
22. J. Larkin, R. Henley, D. C. Bell, T. Cohen-Karni, J. K. Rosenstein and M. Wanunu, ACS Nano, 2013, 7, 10121–10128.
23. K. Liu, J. D. Feng, A. Kis and A. Radenovic, ACS Nano, 2014, 8, 2504–2511.
24. N. Modi, P. R. Singh, K. R. Mahendran, R. Schulz, M. Winterhalter and U. Kleinekathofer, J. Phys. Chem. Lett., 2011, 2, 2331–2336.
25. X. K. Jiang, J. S. Huang, B. G. Sumpter and R. Qiao, J. Phys. Chem. Lett., 2013, 4, 3120–3126.
26. T. J. Macke and D. A. Case, Molecular Modeling of Nucleic Acids, 1998, vol. 682, pp. 379–393.
27. J. T. B. D. A. Case, R. M. Betz, D. S. Cerutti, T. E. Cheatham III, T. A. Darden, R. E. Duke, T. J. Giese, H. Gohlke, A. W. Goetz, N. Homeyer, S. Izadi, P. Janowski, J. Kaus, A. Kovalenko, T. S. Lee, S. LeGrand, P. Li, T. Luchko, R. Luo, B. Madej, K. M. Merz, G. Monard, P. Needham, H. Nguyen, H. T. Nguyen, I. Omelyan, A. Onufriev, D. R. Roe, A. Roitberg, R. Salomon-Ferrer, C. L. Simmerling, W. Smith, J. Swails, R. C. Walker, J. Wang, R. M. Wolf, X. Wu, D. M. York and P. A. Kollman, AmberTools 15, 2015, http://ambermd.org/.
28. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33.
29. S. V. Sambasivarao and O. Acevedo, J. Chem. Theory Comput., 2009, 5, 1038–1050.
30. B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447.
31. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
32. M. Bester-Rogac, A. Stoppa, J. Hunger, G. Hefter and R. Buchner, Phys. Chem. Chem. Phys., 2011, 13, 17588–17598.
33. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
34. H. J. C. Berendsen, J. P. M. Postma, W. F. v. Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
35. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
36. W. Lv, S. Liu, X. Li and R. Wu, Electrophoresis, 2014, 35, 1144.
37. A. Aksimentiev and K. Schulten, Biophys. J., 2005, 88, 3745–3761.
38. J. K. Rosenstein, M. Wanunu, C. A. Merchant, M. Drndic and K. L. Shepard, Nat. Methods, 2012, 9, 487–492.
39. R. M. M. Smeets, U. F. Keyser, N. H. Dekker and C. Dekker, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 417–421.
40. C. Tasserit, a. Koutsioubas, D. Lairez, G. Zalczer and M. C. Clochard, Phys. Rev. Lett., 2010, 105, 1–4.
41. G. Biroli, Nat. Phys., 2007, 3, 222–223.
42. B. M. Venkatesan, D. Estrada, S. Banerjee, X. Jin, V. E. Dorgan, M.-H. Bae, N. R. Aluru, E. Pop and R. Bashir, ACS Nano, 2012, 6, 441–450.
43. A. Chandran, D. Ghoshdastidar and S. Senapati, J. Am. Chem. Soc., 2012, 134, 20330–20339.
44. L. Liang, P. Cui, Q. Wang, T. Wu, H. Agren and Y. Tu, RSC Adv., 2013, 3, 2445–2453.
45. M. Davenport, A. Rodriguez, K. J. Shea and Z. S. Siwy, Nano Lett., 2009, 9, 2125–2128.
46. J. Han, J. Fu and R. B. Schoch, Lab Chip, 2008, 8, 23–33.
47. W. M. Deen, AIChE J., 1987, 33, 1409–1425.
48. C. A. Merchant, K. Healy, M. Wanunu, V. Ray, N. Peterman, J. Bartel, M. D. Fischbein, K. Venta, Z. Luo, A. T. C. Johnson and M. Drndić, Nano Lett., 2010, 10, 2915–2921.
49. W. K. Stefan, Y. G. Alexander, R. Yitzhak and D. Cees, Nanotechnology, 2011, 22, 315101.
50. C. C. Shi, Z. Kong, T. Y. Sun, L. J. Liang, J. W. Shen, Z. Y. Zhao, Q. Wang, Z. Z. Kang, H. Agren and Y. Q. Tu, RSC Adv., 2015, 5, 9389–9395.
51. S. Kesselheim, W. Müller and C. Holm, Phys. Rev. Lett., 2014, 112, 018101.
52. J. Li, Y. Zhang, J. Yang, K. Bi, Z. Ni, D. Li and Y. Chen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 062707.
53. A. Aksimentiev, J. B. Heng, G. Timp and K. Schulten, Biophys. J., 2004, 87, 2086–2097.
54. B. Luan and A. Aksimentiev, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 021912.
55. B. Luan and A. Aksimentiev, Soft Matter, 2010, 6, 243–246.
56. S. A. Kislenko, I. S. Samoylov and R. H. Amirov, Phys. Chem. Chem. Phys., 2009, 11, 5584.
57. R. Qiao and N. R. Aluru, Phys. Rev. Lett., 2004, 92, 198301.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra07017e

---