Computational study of the structure, UV-vis absorption spectra and conductivity of biphenylene-based polymers and their boron nitride analogues

Abstract

In the present study, we calculated the electronic and spectral properties of the one- and two-dimensional carbon and boron nitride materials composed of four-, six- and eight-membered rings (the (4, 6, 6, 8) topology) on the basis of density functional theory, including the band structure analysis for the infinite structures. We found that biphenylene-based two-dimensional (2D) sheets and zigzag-type biphenylene-based one-dimensional (1D) ribbons exhibit a semi-metal character. At the same time, the armchair 1D biphenylene-based ribbons possess a narrow-band-gap structure, while boron nitride 2D sheets, 1D zigzag- and armchair-type ribbons exhibit a wide-band-gap semiconducting nature. Simple single-point calculations with a periodic boundary condition generally underestimate the band-gap values in comparison with band structure calculations accounting for the supercell optimization. But in the general case, both approaches provide a correct explanation of the band-gap value. In this work, we also performed for the first time computational modelling of a novel porous biphenylene-based wide-band-gap carbon allotrope, which demonstrated the complexation ability relative to metal atoms forming the metal–carbon intercalates.

---

Introduction

Over the last few decades, the structural study of carbon allotropes has been a focus of many scientific studies and is expected to continue to be widely used for nanoscience and nanotechnology. Indeed, carbon is a unique element that can form numerous combinations with covalent pairing of the sp³-, sp²- and sp-hybridized states. It provides a rich background for the existence of various carbon allotropes.¹ For a long time, diamond, graphite and amorphous carbon were the most well-known carbon allotropes. The synthesis of fullerenes,^1d carbon nanotubes^1e and, of course, graphene^1f,g led to a great explosion in material sciences and nanoengineering. The common feature of graphene, fullerenes and nanotubes is that they are strongly conjugated systems that are maintained in either zero-dimension, quasi-one- or two-dimensional forms. The presence of conjugation and strong electron correlation features leads to a pronounced redox activity and unusual electronic properties of these materials.

Graphene is one of the most promising materials for the next generation of high-speed and nanoscale electronics,² spintronics,^3a,b chemical sensors,^3c,d energy generation and storage devices,^4a–c graphene-based composite materials^4d,e and even DNA sequencing^4f,g because of its peculiar physical properties, including the anomalous room temperature quantum Hall effect,^2b,5a massless Dirac fermion behaviour,^5b–d high carrier mobility at room temperature (250 000 cm² V⁻¹ s⁻¹),^5b,e remarkable thermal conductivity (5000 W m⁻¹ K⁻¹)^5f and excellent mechanical properties with a Young's modulus of 1 TPa.^5g However, pristine graphene is a gapless semiconductor, which limits its use in some electronic applications.⁶ Therefore, a number of different approaches have been proposed to expand the band gap in graphene. The quantum size effects,⁷ symmetry breaking of the hexagonal graphene sheet,⁸ surface and edge modifications,⁹ doping and adsorbing atoms or molecules on the graphene surface¹⁰ do afford the capability to effectively modulate graphene's electronic properties. For example, the symmetry breaking of the initial graphene with a (6, 6) topology can be achieved by the introduction of the four-, five-, seven-, eight- or even twelve-membered rings. In this case the pentaheptite (5, 7),^11a pentahexoctite (5, 6, 8),^11b haeckelite (5, 7, 6),^11c biphenylene-based (4, 6, 6, 8),^11d–f graphenylene (4, 6, 6, 12),^12a planar and buckled T-graphene^12b,c allotropes are reported to be metallic species, while the (4, 8) carbon sheet,^13a cubic porous carbon allotrope C₉₆ (ref. 13b) and bct-C₄-carbon^13c are predicted to be semiconducting allotropes, with a band gap of 0.36, 1.85 and 2.56 eV, respectively. Among these, the (4, 6, 6, 8) carbon topology demonstrates the most promising size- and shape-depending conductivity, exhibiting a metal or semiconducting nature.^11f For example, two-dimensional (2D) sheet and planar strips with zigzag-type edges represent a metallic character, whereas the narrowest armchair strip (0.62 nm wide) presents a large band gap of 1.71 eV, while the 2.14 nm wide armchair strip exhibits a band gap of 0.08 eV.^11d The M-carbon,^13d chiral C₆,^13e F-carbon^13f and W carbon^13g are considered as insulating materials, with band gaps of 3.60, 3.72, 4.12 and 4.39 eV, respectively. The Cco-C₈ allotrope (E_g = 3.12 eV) was found to be energetically more favourable than the earlier proposed M-carbon, bct-C₄, W-carbon and chiral C₆ carbon polymorphs.^13e

Other interesting three-dimensional (3D) metallic carbon allotropes, named as T6- and T14-carbon, consisting of interlocking hexagons were predicted by Jena et al.^14a They also proposed a 2D pentagon-based carbon allotrope or penta-graphene with a band gap of 3.25 eV.^14b Similar graphene allotropes composed of 5–6–7 carbon rings (penta–hexa–hepta-graphene or phagraphene) were designed by A. R. Oganov et al.^14c An unusual feature of the phagraphene is a distortion of Dirac cones.^14c

The rapid progress in graphene and graphene-like material science has strongly motivated researcher's interest to search for novel 2D materials consisting of heteroatoms or their combinations. Initially, following the same methodology as for graphene, Novoselov et al.^15a isolated the individual monolayers of h-BN, dichalcogenides (such as MoS₂ and NbSe₂) and complex oxides (such as Ba₂Sr₂CaCu₂O_x) from their multilayered materials. Since then, numerous other graphene-like materials, including silicene,^15b,c germanene,^15d BC₃,^15e the transition metal carbides Ti₃C₂ (ref. 15f) and Ti₂C,^15g porphyrin-^16a and tetraoxa[8]circulene-based sheets^16b–f and some other materials,¹⁷ have been studied both theoretically and experimentally. These 2D nanostructures listed above also exhibit a number of fascinating dimension-related properties. For instance, hexagonal BN-nanosheets are more stable than their carbon counterparts and possess excellent insulating properties, good thermal conductivity, extraordinary mechanical strength and a high resistance to oxidation that allows their use in graphene-based electronics.^17c

The carbon and boron nitrides (BNs) have a lot of related structures, such as diamond and cubic BN,^18a graphitic forms of carbon and boron nitride,^18b,c fullerenes^18d and nanotubes.^18e Recently, some new boron nitride allotropes were reported¹⁹ in succession and their electronic structure and properties were successfully studied. Recently, Yakobson et al.^19d studied various dislocations and grain boundaries in 2D hexagonal boron nitride (h-BN). In particular, a new dislocation structure was discovered involving a square-octagon pair (4|8) in a h-BN-sheet, which was more energetically favourable than the corresponding pentagon–heptagon pairs (5|7).^19d In this paper, we describe the 1D and 2D structures of boron nitride allotrope with the (4, 6, 6, 8) topology in comparison with the same pure carbon species. The dynamic stability of the infinite carbon structures with the (4, 6, 6, 8) topology was previously validated on grounds of the phonon-mode analysis.^20a,b Subsequently, the finite iodine-containing biphenylene (Bp) ribbons were synthesised by Müllen et al.^20c However, the electronic structure, spectra and conductivity of the Bp-based materials are still unstudied, except for in ref. 20a, in which the electronic properties of the biphenylene sheet and its 1D derivatives were studied by density functional theory (DFT) calculations. In the present paper, we additionally study the structure and UV-vis absorption spectra of the 1D and 2D Bp-based species with different sizes and chiralities, as well as proposing here for the first time a novel porous tunnel-like carbon allotrope that is able to include metal atoms (Li as an example) to form metal–carbon intercalates. The studied compounds may hold promise for their application in modern electronic systems, similar to graphene and boron nitride with the generally known (6, 6) topology.

Method of calculation

The finite Bp- and BN-based 1D and 2D structures (Fig. 1), the “tunnel” carbon allotrope (Fig. 2–4) and its Li-containing complexes (Fig. 4) were optimized on the grounds of a DFT^21a,b approach using the B3LYP/6-31G(d)²¹ method with control of the possible symmetry constraints, using the Gaussian 09 software package.²² The absence of imaginary vibrational wavenumbers in the calculated IR spectra indicates that all the stationary points correspond to genuine minima. The electronic spectra of the Bp- and BN-based 1D and 2D structures were calculated by the time dependent (TD) DFT method in the vacuum approximation using the same B3LYP/6-31G(d)²¹ method. The optical spectra could be better approximated with other functionals such as CAM-B3LYP^21e or wB97xd.^21f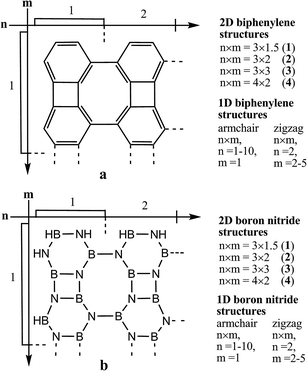

Fig. 1 The structure of the Bp and BN compounds (where n and m denote the number of fragments along the horizontal and vertical directions, respectively).

Fig. 2 The lattice parameters together with the symmetry unique bond lengths (in Å) and selected angles (in degrees) for periodic models of the studied species.

Fig. 3 Electronic absorption spectra of the Bp- and BN-sheets and ribbons calculated by the TD DFT/B3LYP/6-31G(d) method (band half-width 1500 cm⁻¹, Gaussian distribution function).

Fig. 4 The optimized structure of the tunnel-like carbon allotrope (a), lithium-containing complex with a macrocyclic tunnel-like ligand (b), and the prism-shaped coordination cage comprising Li atoms (c) (green: carbon atoms; white: hydrogen atoms; magenta: lithium atoms).

For the “tunnel” carbon allotrope, we also performed the population analysis by the natural bond orbital (NBO) method^23a at the same level of DFT using the NBO module^23b within the Gaussian 09 package. For the optimized geometry of the simplest Li-containing complex (Fig. 4), we carried out a topological analysis of the electron density distribution function ρ(r) by the quantum theory of atoms in molecules (QTAIM) method.²⁴ The energies of the coordination Li–C bonds were estimated by the following relationship:²⁵

E = 0.5ν(r), (1)

where E is the bond energy (a.u.) and ν(r) is the potential energy density (a.u.) in the corresponding (3, −1) bond critical point.²⁴

The electronic origin of the Li–C bonds has been qualitatively described on the grounds of the electron density Laplacian ∇²ρ(r) and by electron energy density h_e(r) analysis of the corresponding (3, −1) bond critical points.^24,26

The periodic DFT calculations ware performed using the Cambridge Serial Total Energy Package (CASTEP) module²⁷ implemented in the Materials Studio 5.5 program suite.²⁸ The exchange and correlation interactions were described using the generalized gradient approximation (GGA) approach with the functional parameterized by Perdew–Burke–Ernzerhof (PBE).²⁹ An ultrasoft pseudopotential was used to describe the electron–core interactions and its representation was performed in a reciprocal space. For the geometry optimization, the electronic wave functions were expanded in a plane wave basis set with an energy cut-off of 500 eV. Thereafter, a denser k-point mesh, as well as a more extended basis set (with a 600 eV energy cut-off) was applied for the band structure calculation.

To examine the stability of the Bp-, BN-based sheets and tunnel-like carbon allotrope, we calculated the cohesive energy (E_coh) using the following formula:^13a

E_coh = [E_tot.(structure) − NE(atom)]/N (2)

where E_tot.(structure) and E(atom) are the total electronic energies of the corresponding unit cell (Bp-, BN-based sheet or tunnel-like carbon allotrope) and single carbon, boron or nitrogen atoms, respectively, and N is the total number of the corresponding types of atoms in the studied structure.

All the calculations were performed in terms of the supercell approximation. In the case of the ribbon structures, a 15 Å vacuum slab was added in the two perpendicular directions in order to avoid the unphysical interactions between the neighbouring ribbons. The highest possible symmetry was specified before starting the geometry optimization in all the cases. Thus, the studied structures fell into the following space groups: Pmmm (Bp-sheet); Pmmm (zigzag Bp-ribbon); Pmmm (armchair Bp-ribbon); P4/mmm (tunnel-like carbon allotrope); Pmma (BN-sheet); Pmma (zigzag BN-ribbon) and P2/m (armchair BN-ribbon).

Results and discussion

1. Structural features

All the studied Bp-based 1D zigzag- and armchair-type ribbons and 2D sheets have a planar structure (D_2h symmetry point group). The novel designed 1D and 2D BN compounds consisting of equal numbers of nitrogen and boron atoms are isoelectronic analogues to the similarly structured carbon counterparts. Generally, these Bp- and BN compounds represent the graphene and boron nitride allotropes, respectively, both formed by a combination of the four-, six- and eight-membered rings in the one- or two-dimensions, similarly to the well-known graphene and boron nitride modifications with hexagonal structures.

The general size properties of the studied Bp- and BN representatives of the (4, 6, 6, 8) topology are presented in Table 1. In contrast to the Bp-structures, the BN-based ribbons and sheets possess the C_2h symmetry point group in the ground singlet state (Fig. 1). All the bond lengths in the simplest BN-ribbon 2 varied in the narrow range of 1.41–1.47 Å (see ESI, S1†). With the growth of the BN cluster, we observed the equalization of the B–N bond lengths (1.43–1.46 Å); in a similar manner the C=C bond length alternation decreases with the increase in the carbon Bp nanoclusters due to the ensuing π-conjugation.

Table 1 The general size properties of the designed Bp- and BN-based sheets and ribbons designed by the B3LYP/6-31G(d) computations^a

Biphenylene compounds	n × m	a, nm*	b, nm**	Empirical formula	Boron nitride compounds	n × m	a, nm*	b, nm**	Empirical formula
a *a or **b – width or length of the corresponding Bp- and BN-based structures.
1	3 × 1.5	1.20	1.39	C54H18	1	3 × 1.5	1.23	1.42	B27H18N27
2	3 × 2	1.39	1.58	C72H20	2	3 × 2	1.59	1.42	B36H20N36
3	3 × 3	2.34	1.39	C108H24	3	3 × 3	2.36	1.42	B54H24N54
4	4 × 2	1.58	1.84	C96H24	4	4 × 2	1.59	1.87	B48H24N48
1D armchair ribbons (m = 1)	1	0.81	0.51	C12H8	1D armchair ribbons (m = 1)	1	0.82	0.52	B6H8N6
	2	0.81	0.95	C24H12		2	0.82	0.96	B12H12N12
	3	0.81	1.39	C36H16		3	0.82	1.41	B18H16N18
	4	0.81	1.83	C48H20		4	0.82	1.86	B24H20N24
	5	0.81	2.28	C60H24		5	0.82	2.31	B30H24N30
	6	0.81	2.72	C72H28		6	0.82	2.76	B36H28N36
	7	0.81	3.16	C84H32		7	0.82	3.20	B42H32N42
	8	0.81	3.60	C96H36		8	0.82	3.65	B48H36N48
	9	0.81	4.04	C108H40		9	0.82	4.10	B54H40N54
	10	0.81	4.49	C120H44		10	0.82	4.55	B60H44N60
1D zigzag ribbons (n = 2)	2	1.15	0.95	C48H16	1D zigzag ribbons (n = 2)	2	1.59	0.97	B24H16N24
	3	2.34	0.95	C72H20		3	2.36	0.97	B36H20N36
	4	3.10	0.95	C96H24		4	3.12	0.97	B48H24N48
	5	3.87	0.95	C120H28		5	3.89	0.97	B60H28N60

---

It is interesting to note that the difference in the total energies of the BN systems with the (4, 6, 6, 8) topology and the isomeric “classical” (6, 6) topologies is significantly less in comparison with those for the Bp-systems. For example, the total energy for the BN cluster (n × m = 2 × 1) is higher by ≈84 kcal mol⁻¹ in comparison with the isomeric hexagonal B₁₂H₁₂N₁₂. As we have noted previously,^11f the difference in total energies for Bp-isomers with (4, 6, 6, 8) and (6, 6) topologies is about ≈130 kcal mol⁻¹. Thus, we can conclude that the hexagonal Bp- and BN compounds are more stable relative to the (4, 6, 6, 8) topology. But this fact does not exclude the existence of stable isomeric (4, 6, 6, 8) forms that can be transformed into the corresponding graphene and boron nitride (6, 6) clusters by overcoming the isomerization energy barrier.

The lattice parameters and geometrical data for the periodic models of the studied compounds are presented in Fig. 2. For Bp-sheets, the bond lengths in the hexagons are pairwise equal at 1.458 and 1.406 Å, respectively, while the four-membered ring represents almost a perfect square (1.446 and 1.458 Å, Fig. 2a). For BN-sheets (Fig. 2f), the octa- and tetragons are significantly distorted relative to the Bp analogue (the bond angles in the tetragons equal 97° and 83° instead of 90° in the Bp-sheets). Due to the symmetry distortion in the BN-sheets, the B–N distances are almost nonequivalent and range from 1.434 to 1.479 Å (Fig. 2f). For both armchair and zigzag Bp-ribbons (Fig. 2b and c), we observed a strong bond length alternation.

We can distinguish the series of short (1.385–1.401 Å) and long C–C bonds (1.417–1.517 Å) due to the edge effect. In contrast, the B–N distances for both types of BN-ribbons cover the shorter range (1.421–1.482 Å, Fig. 2d and e), i.e. the edge effects are less influential due to the absence of π-conjugation. It is interesting that the calculated cohesive energy of the (4, 6, 6, 8) BN-sheet is 8.52 eV per atom, which is higher than for the hexagonal BN (calc. 7.91 (ref. 30a)/exp. 6.65 (ref. 30b) eV per atom).

The lattice structural parameters for the porous tunnel-like carbon allotrope are discussed in paragraph 3 of this section. The calculated cohesive energy of the tunnel-like carbon allotrope is 8.64 eV per atom, which is 0.28 eV higher than for the (4, 6, 6, 8) carbon sheet (8.36 eV per atom) and much higher than for many other stable carbon allotropes.^13a

2. Analysis of the electronic absorption spectra

The calculated electronic absorption spectra of the Bp- and BN-based ribbons and sheets are presented in Fig. 3. The electronic structure and spectrum of the initial biphenylene molecule have been previously published and are well described.³¹ In particular, the biphenylene spectrum includes a group of well-defined bands from 400 to 313 nm.^31a Carr et al. showed that the first low intensity band could be observed at 391 nm and it was overlapped by one of the more intense bands at 358 nm.^31a Later on, Hilpern J. W.^31b interpreted these bands as vibronically active. He also showed that the phosphorescence and fluorescence of biphenylene occur from the second electronic state. This behaviour is also well known for a number of other polycyclic hydrocarbons.^31d

Our DFT calculations for the free biphenylene molecule also indicated that the first electronic transition (369 nm) is symmetry forbidden (X¹A_g → 1¹B_3g) in the electric-dipole approximation but it is allowed as a magnetic-dipole transition. Although magnetic–dipole transition moment is rather large (2.19 Bohr magneton), its contribution to the oscillator strength is negligible. The transition into the S₂ exited state is symmetry allowed and was calculated at 310 nm with a comparatively weak intensity (f = 0.08, see ESI, Table S2†).

The next very intense absorption band takes place in the UV region with a maximum at 248 nm (ref. 31a) and can be assigned to the electronic transition of the X¹A_g → 2¹B_1u symmetry into the S₄ excited state at 231 nm (see ESI, Table S2†).

The absorption spectra of the designed Bp- and BN compounds represent a similar two-band shape, but the size of the nanoclusters strongly affects the bands position, i.e. in terms of the electronic transition energies (see ESI, Tables S2 and S3,† also Fig. 3). For the armchair Bp-ribbons (n = 2–10), the first broad band has a low intensity and takes place in the region of 400–470 nm (Fig. 3a), which we assigned to the transitions of X¹A_g → ¹B_2u symmetry (within the D_2h point group). With the increase in the ribbon length, the first band shifts to red, but a number of low-lying singlet excited states appear before the main transition of the band I onset. The second short-wavelength band of high-intensity takes place in the UV region for the short oligomers, but with the growth of the ribbon size, this band shifts to the visible region.

Unlike the armchair samples, the first broad band for the zigzag Bp-ribbons (m = 2–5) is much more intense and takes place in a wide visible and near IR range of 500–1100 nm (Fig. 3b), depending of the length of the ribbon. This band corresponds to electronic transitions of the X¹A_g → 3¹B_1u symmetry (see ESI, Table S2†), which are characterized by high oscillator strength values (Fig. 3b). Moreover, the first band intensity correlates well with the total area of the zigzag Bp-ribbons (Table 1). The second much less intensive absorption band in the spectra of the zigzag Bp-ribbons (m = 2, 3) is predicted to be in the range of 300–500 nm due to the high-lying transitions of X¹A_g → ¹B_1u symmetry (see ESI, Table S2†). For the larger zigzag Bp-ribbons of size n × m = 2 × 4 and n × m = 2 × 5, the second absorption band disappears because the corresponding electronic transitions becomes very weak (f ≈ 0.004); it also turns out to be overlapped, since the gap between the I and II bands diminishes.

A size-dependent absorption was also observed for the 2D Bp-sheets. We found that the absorption spectra of the 2D sheets were characterized by an intense size-dependent absorption in the visible-NIR region of 550–1000 nm (the first band) (Fig. 3c, also see ESI, Table S2†). A second, less intense, absorption band takes place in the range of 300–350 nm (Fig. 3c). Both bands in their spectra are characterized by increasing absorption intensity, with the subsequent growth of Bp-sheets in both directions. This indicates a key role of the π-conjugation effect, similar to with polyenes, polyacenes and other strongly conjugated systems.

The calculated parameters of the electronic absorption spectra for the BN-polymers are presented in the ESI, Table S3.† Here, an important observation is the absence of visible absorption in the spectra of the BN-ribbons and BN-sheets due to the absence of π-conjugation in the BN-polymers, in contrast to the Bp-polymers. The electronic transitions of all the BN-polymers occur in the middle ultraviolet region (Fig. 3d–f). For example, the armchair BN-ribbons (n = 2–10) exhibit weak absorption in the range of 225–235 nm (Fig. 3d) (the first band) and a strong blue-shifted absorption in the range of 195–220 nm (the second band). For the zigzag BN-ribbons, both bands in the UV spectra are slightly shifted to a longer wavelength (Fig. 3e).

Another feature of the electronic spectra of BN compounds is a high density of excited singlet sates (see ESI, Table S3†). For instance, in the calculated spectrum of the BN-sheet sized n × m = 3 × 1.5 (Fig. 2f), the absorption in the range of 240–265 nm (Fig. 3f) corresponds to a combination of twenty close-lying electronic transitions (the four most intense of them are presented in the ESI, Table S3†). While 1D and 2D Bp-polymers absorb in the visible region, the BN-polymers exhibit higher excitation energies that fall in the UV region (4.4–6.2 eV). Thus indicating that BN-polymers may be useful as UV light protectors.

3. The tunnel-like carbon allotrope and its Li-containing complexes

In this paragraph, we present for the first time computational modelling of the novel tunnel-like carbon allotrope. The simplest porous cluster (D_2h symmetry point group) of the (4, 6, 6, 8) topology can be represented as a covalence stacked dimmer of the n × m = 2 × 1 species (Fig. 4a). The calculated bond lengths and the natural charges at the carbon atoms are presented in Table 2. We found that the studied cluster included short double (1.337, 1.341 Å, Table 2) and long saturated (1.523–1.691 Å, Table 2) bonds. Being 1.496 Å (Table 2) in length, the C1–C8 bond was indicated as being an intermediate type due to a partial π-bond contribution. The C5–C10 and C8–C11 distances in the studied cluster (Fig. 4a) were extremely large (1.636 and 1.691 Å, respectively) but were close to the long CC distances for 2-(1-diamantyl)[121]tetramantane observed by Fokin et al.³²

Table 2 The bond lengths and the NBO atomic charges for the carbon atoms of the tunnel-like carbon allotrope calculated by the DFT/B3LYP/6-31G(d) method

Bond	Bond length, Å	Atom	Natural charge
C1–C2	1.341	C1, C4	0.0086
C1–C4	1.596	C2, C3	0.0099
C2–C3	1.567	C5, C10	−0.2907
C2–C5	1.508	C6	−0.1920
C5–C6	1.530	C7	−0.1954
C6–C7	1.337	C8, C9, C11	−0.0696
C7–C8	1.523
C1–C8	1.496
C8–C9	1.557
C5–C10	1.636
C8–C11	1.691

---

As can bee seen from the natural bond orbital (NBO) analysis data (Table 2), the most negative charges (−0.29e) are located on the C5 and C10 carbon atoms. The natural electron configurations of these atoms are 1s²2 s^0.9822p^3.29, which is very close to the 1s²2s¹2p³ configuration expected for a tetrahedral carbon. All the atoms included in the four-membered rings differ from other carbon atoms by the small positive natural charge (0.0086 and 0.0099e for C1, C4 and C2, and C3 atoms, respectively) with a number of electrons on these atoms equal to 5.99 (Table 2).

The calculated occupancies of the natural orbitals and the natural hybrids on the carbon atoms of the tunnel-like carbon allotrope are presented in Table 3. We suggest that the carbon atom C1 forms single sigma bonds with its C4 and C8 neighbours and also double σ + π bonds with the C2 atom. The sigma bond between the C1 and C2 atoms results from the overlap between the sp^1.81 hybrid on C1 and the sp^1.85 hybrid on C2 (Table 3). The π(C1–C2) bond originates from the almost pure p orbital on the C1 and C2 atoms. The σ(C1–C4) bond is formed by the same sp^2.62 hybridized C1 and C4 atoms, with an approximate composition of 27.64% s and 72.31% p atomic orbitals. On the other hand, the σ(C1–C8) bond is formed from the sp^1.73 hybrid character on the C1 atom (which is a mixture of 36.61% s and 63.35% p atomic orbitals). A similar analysis can be applied for all the other bonds in accordance with the NBO data from Table 3.

Table 3 Occupancy of natural orbitals (NBOs) and hybrids of carbon atoms in the tunnel-like carbon allotrope calculated by the DFT/B3LYP/6-31G(d) method

C–C type bond	Occupancy	Hybrid	AO (%)
σ(C1–C2)	1.96375	C1: sp^1.81	C1: s (35.63%) p (64.32%) d (0.05%)
		C2: sp^1.85	C2: s (35.12%) p (64.83%) d (0.05%)
π(C1–C2)	1.92401	C1: p	C1: s (0.00%) p (99.93%) d (0.07%)
		C2: p	C2: s (0.00%) p (99.93%) d (0.06%)
σ(C1–C4)	1.94957	C1, C4: sp^2.62	C1, C4: s (27.64%) p (72.31%) d (0.05%)
σ(C1–C8)	1.96759	C1: sp^1.73	C1: s (36.61%) p (63.35%) d (0.04%)
		C8: sp^2.69	C8: s (27.12%) p (72.83%) d (0.05%)
σ(C2–C3)	1.95564	C2, C3: sp^2.49	C2, C3: s (28.66%) p (71.29%) d (0.05%)
σ(C2–C5)	1.97385	C2: sp^1.77	C2: s (36.09%) p (63.87%) d (0.04%)
		C5: sp^2.83	C5: s (26.12%) p (73.83%) d (0.05%)
σ(C5–C6)	1.96686	C2: sp^2.90	C5: s (25.66%) p (74.29%) d (0.05%)
		C5: sp^2.19	C6: s (31.30%) p (68.65%) d (0.04%)
σ(C5–C10)	1.93091	C5, C10: sp^3.16	C5, C10: s (24.04%) p (75.93%) d (0.04%)
σ(C6–C7)	1.98159	C6: sp^1.61	C6: s (38.31%) p (61.65%) d (0.04%)
		C7: sp^1.59	C7: s (38.57%) p (61.39%) d (0.04%)
π(C6–C7)	1.95656	C6: sp	C6: s (0.00%) p (99.93%) d (0.06%)
		C7: sp	C7: s (0.00%) p (99.93%) d (0.06%)
σ(C7–C8)	1.96116	C7: sp^2.19	C7: s (31.32%) p (68.63%) d (0.05%)
		C8: sp^2.72	C8: s (26.84%) p (73.11%) d (0.05%)
σ(C8–C9)	1.97038	C8, C9: sp^2.70	C8, C9: s (27.02%) p (72.93%) d (0.05%)
σ(C8–C11)	1.88727	C8, C11: sp^3.28	C8, C11: s (18.94%) p (81.03%) d (0.04%)

---

We also DFT-designed the Li-containing complex with the tunnel-like cluster (Fig. 4b). Recently, Liu et al.^33a presented the theoretical results of the DFT study of Li-decorated T-graphene as a feasible nanosensor. The role of Li doping on band-gap modulation and charge-transfer in band-gap engineering was studied in ref. 33b and c We can generalize that carbon allotropes provide a rich source for the creation of new carbon materials beyond a hexagonal symmetry for applications for the detection of polluting gases.

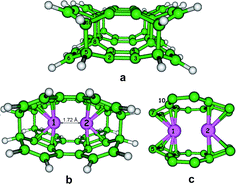
We found that the simplest cluster can include an inner cavity of two Li atoms with a Li–Li distance of 1.72 Å. In order to understand the chemical nature of Li inclusions, we analyzed the metal–ligand bonding nature for the studied lithium-containing complex (Fig. 4b) in the framework of the Bader's theory formalism.²⁴ Each Li atom is included into the carbon cluster by the sandwich-type principle. Eight Li1–C and Li2–C bonds are equivalent in terms of the bond length and electronic criteria for the designed complex (Table 4). The lithium atoms are located in the middle of cavity, jammed between the two four-membered rings. Therefore, the coordination sphere of each Li atom represents the irregular quadrangular prism inclined by 15° (Fig. 4c) and contains four bonds with a bond length 2.098 Å and four other bonds with a slightly longer length (2.188 Å) (Table 4).

Table 4 Bond length (d) and selected topological parameters of the electron density distribution function ρ(r) of the Li–C bond

Bond	d, Å	ρ(r)^a, e × a0^−3	ν(r), a.u.	g(r), a.u.	he(r)^b, a.u.	∇^2ρ(r)^c, e × a0^−5	E, kcal mol^−1
a a0 is the Bohr radius.b he(r) = ν(r) + g(r), where g(r) is the kinetic energy density at the (3, −1) critical point.c 1/4∇^2ρ(r) = 2g(r) + ν(r).
Li1–C3	2.098	2.6567 × 10^−2	−2.896 × 10^−2	3.481 × 10^−2	0.585 × 10^−2	0.1626	−9.1
Li1–C4
Li1–C9
Li1–C10
Li1–C5	2.188	2.4152 × 10^−2	−2.436 × 10^−2	2.933 × 10^−2	0.497 × 10^−2	0.1372	−7.6
Li1–C6
Li1–C7
Li1–C8

---

QTAIM analysis²⁴ of the Li–C contacts in the studied complex indicated that all the Li–C bonds critical points can be characterized by the following conditions: ∇²ρ(r) > 0 and h_e(r) > 0 (|ν(r)| < g(r)) (Table 4), which allowed us to classify the Li–C contacts as the closed shells interactions. The total complexation energy of the eight Li–C bonds calculated by the Espinosa eqn (1) was −67 kcal mol⁻¹ (Table 4), which defines the great stability of the designed complex.

We also performed a band structure calculation for the 3D periodic model of the tunnel-like carbon allotrope (Fig. 2g). The lattice parameters of the unit cell were equal to 4.560 Å for the a and b axes and 3.861 Å for the c axis; all the CC bond lengths varied in a short range from 1.514 to 1.584 Å (Fig. 2g). As one can see in Fig. 5, this allotrope possesses a wide-band-gap semiconducting nature. The partial density of states (PDOS) plot specifies the tunnel-like carbon allotrope as a material similar to the p-type extrinsic semiconductor. There is no DOS at or above the Fermi level, which is shifted down to the VBM. Near the Fermi level, the DOS almost completely consists of carbon 2p states (Fig. 5). The positions of the valence band maximum (VBM) and conducting band minimum (CBM) indicate a direct band gap of 2.985 eV (Fig. 5). An interesting feature is that the VBM occurs not at the Γ-point (indicated by a circle). It is known that for bulk materials this is often the case, whereas for monolayered materials, the VBM occurs at the K-point rather than at the Γ-point.³⁴ We speculate that this is related with the 2D nature of the bonding in the studied tunnel-like carbon allotrope. Thus, the latter can be characterized as a partially layered material.

Fig. 5 The band structure and partial density of states of the 3D periodic tunnel-like carbon allotrope.

4. Band-gap engineering

Band-gap engineering³⁵ is a powerful technique for the creation of novel materials, such as the biphenylene and boron nitride sheets and ribbons, which allows researchers to control or change the band gap of different polymers.

As one can see from Fig. 6, the HOMO-LUMO gap (HLG) can be represented as a function of the oligomer size (1/n) for the studied 1D and 2D Bp- and BN-based structures. For the 2D Bp-sheets, the band-gap values decrease considerably stronger (by ∼3.0 eV) than for the BN-sheet (by ∼1.3 eV) when the polymer (n → ∞) is compared with the initial Bp- and BN units (1/n = 1), respectively. The infinite structures calculated with the periodic boundary conditions (PBC) model demonstrate a close-to-zero band gap for Bp-sheets and a significantly wider band-gap for BN-sheets, which was equal to 4.46 eV (Fig. 6a).

Fig. 6 The size dependence behaviour of the band gap for the Bp- (a) and BN-based (b) 1D and 2D oligomers/polymers (where n and m denote the numbers of the Bp- or BN-monomers along the horizontal and vertical directions, respectively).

For 1D armchair Bp-ribbons, the band-gap values shrink more slowly in comparison with 2D Bp-sheets and 1D zigzag-type Bp-ribbons when n → ∞ compared with the initial Bp-unit (Fig. 6). The DFT calculations of the PBC models demonstrate the finite band-gap values of 2.14 and 0.24 eV for armchair and zigzag-type Bp-ribbons, respectively (Fig. 6b).

In contrast to Bp-ribbons, both armchair and zigzag-type BN-strips demonstrate a wide-band-gap nature, which tends to show a monotonic decrease with the ribbon growth. It should be noted that the infinite armchair and zigzag BN-based ribbons exhibit band gaps of 5.17 and 4.65 eV, respectively (Fig. 6b).

The aforementioned results are in a good agreement with the band structure calculations (Fig. 7). Thus, in the case of the Bp-sheets (Fig. 7a), the calculations reveal a semi-metal nature of this species. The positions of VBM and CBM specify an indirect gap. This is in good agreement with the PBC single-point calculation, which provides the HLG to be equal to 0.06 eV (Fig. 6a). A similar picture occurs in the case of the zigzag Bp-ribbon (Fig. 7b). Though, within the PBC model, the HLG value is equal to 0.24 eV, the band structure calculations indicate a semi-metal nature of this species. These materials can be used in optoelectronic devices with a photoresponse in the blue and UV regions.^36a

Fig. 7 The band structure and partial density of states of the 1D and 2D structures studied: (a) the Bp-sheet, (b) zigzag Bp-ribbon, (c) armchair Bp-ribbon, (d) the BN-sheet, (e) zigzag BN-ribbon and (f) armchair BN-ribbon.

The partial density of states (DOS) plot (Fig. 7a) demonstrates a rather high density of states at the Fermi level in the Bp-sheet. This is caused by an overlap of the valence and conducting bands and predominantly consists of the p electrons. The same pattern is observed in the case of the zigzag Bp-ribbon (Fig. 7b).

In the case of the armchair Bp-ribbon (Fig. 7c), the band structure calculations displays a semiconducting nature with a direct gap equal to 1.047 eV. The PBC single-point calculations, however, significantly overestimate this value (2.14 eV). It is interesting that the Fermi level is significantly shifted to the valence band (Fig. 7c). This pattern is similar to the p-type extrinsic semiconductors. There are no overlapping bands in the case of the armchair Bp-ribbon, where the aforementioned proximity of the valence band and the Fermi level causes a non-vanishing density of states (Fig. 7c); as in the previous, cases the DOS includes the p electrons. Thus, at a finite temperature, the armchair Bp-ribbon can behave as a semi-metal. This structure possesses promising characteristics for the field of solar-energy conversion using a single junction photovoltaic cell.^36b

Concerning the BN structures, both the BN-sheets (Fig. 7d) and the BN-ribbons (Fig. 7e and f) possess a semiconducting nature with the direct band gaps. There is also a non-vanishing DOS at the Fermi level, but the band-gap values are large enough to neglect the possibility of the electron injections in the conducting band at a finite temperature. Again, the PBC calculation at the HLG limit overestimates the band-gap values: 4.46 versus 3.23 eV (BN-sheets), 4.65 versus 3.43 eV (zigzag BN-ribbons) and 5.17 versus 4.11 eV (armchair BN-ribbons). Nevertheless, the values of HLG obtained using the PBC model calculations correlate well with the band-gap values, showing the correlation coefficient to be equal to R² = 0.9995. We should also stress that the same shift of the Fermi level is observed in the latter three cases. Such wide-band-gap semiconductors could be attractive materials for aerospace power systems and transportation.^36c

Conclusions

Using the DFT method, we systematically studied the electronic structure and spectral properties of biphenylene and boron nitride materials formed by a combination of the four-, six- and eight-membered rings. The following conclusions can be made:

(1) The constructed one- and two-dimensional biphenylene and boron nitride structures were found to be absolutely planar in the ground state. In contrast to biphenylene-based polymers, the boron nitride 1D and 2D materials undergo a symmetry reduction to the C_2h symmetry point group.

(2) All the studied 1D and 2D biphenylene- and boron nitride compounds were characterized by a strong size-dependent absorption in the electronic spectra because of the specific π- and σ-conjugation of Bp- and BN-based polymers, respectively. An important observation is the strong UV absorption in the spectra of the BN compounds, which could be useful for UV light protectors. In turn, the Bp-polymers exhibit a strong visible absorption, which could help them find potential application in solar cell technology.

(3) Our calculations indicated that the band-gap decreases with the subsequent polymer growth. This fact opens up new possibilities for creating novel materials with size-controlled semiconducting properties. The infinite armchair biphenylene strip and all the boron nitride structures are predicted to be organic semiconductors, whereas zigzag biphenylene strips and sheets possess a metallic nature.

(4) The novel tunnel-like carbon allotrope demonstrated a direct band gap of 2.985 eV, indicating its wide-band-gap semiconducting properties. Moreover, it was found that the unique structure of the designed tunnel-like carbon allotrope allows binding lithium atoms, in which their size correlates with the size of the macrocycle cavity. The lithium atoms forming the sandwich-type coordination structure were designed to be included in the inner carbon cavity. All the Li–C bonds could be classified as closed shell interactions.

Acknowledgements

All computations were performed with the resources provided by the Swedish National Infrastructure for Computing (SNIC) at the Parallel Computer Center (PDC) through the project “Multiphysics Modelling of Molecular Materials”, SNIC 020/11-23. This research was also supported by the Ministry of Education and Science of Ukraine (project number 0115U000637). B. F. M. expresses his gratitude to the Chinese Academy of Science for financial support in the framework of the presidential international initiative.

Notes and references

1. (a) A. L. Ivanovskii, Russ. Chem. Rev., 2012, 81, 571; (b) Q. Li, Y. Ma, A. R. Oganov, H. Wang, H. Wang, Y. Xu, T. Cui, H.-K. Mao and G. Zou, Phys. Rev. Lett., 2009, 102, 175506; (c) J.-T. Wang, C. Chen and Y. Kawazoe, Sci. Rep., 2013, 3, 3077; (d) H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162; (e) S. Iijima, Nature, 1991, 354, 56; (f) K. Novoselov, et al., Science, 2004, 306, 666; (g) A. H. C. Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109.
2. (a) Z. Chen, Y.-M. Lin, M. J. Rooks and P. Avouris, Phys. E, 2007, 40, 228; (b) K. S. Novoselov, Z. Jiang, Y. Zhang, S. V. Morozov, H. L. Stormer, U. Zeitler, J. C. Maan, G. S. Boebinger, P. Kim and A. K. Geim, Science, 2007, 315, 1379; (c) M. I. Katsnelson, Mater. Today, 2007, 10, 20.
3. (a) A. Candini, S. Klyatskaya, M. Ruben, W. Wernsdorfer and M. Affronte, Nano Lett., 2011, 11, 2634; (b) J. Maassen, W. Ji and H. Guo, Nano Lett., 2011, 11, 151; (c) A. Geim, Nat. Mater., 2007, 6, 183; (d) M. Deng, X. Yang, M. Silke, W. M. Qiu, M. S. Xu, G. Borghs and H. Z. Chen, Sens. Actuators, B, 2011, 158, 176.
4. (a) M. Liu, X. B. Yin, E. Ulin-Avila, B. S. Geng, T. Zentgraf, L. Lu, F. Wang and X. Zhang, Nature, 2011, 474, 64; (b) K. S. Kim, Y. Zhao, H. Jang, S. Y. Lee, J. M. Kim, K. S. Kim, J. Y. Ahn, P. Kim, J. Y. Choi and B. H. Hong, Nature, 2009, 457, 706; (c) Y. W. Zhu, S. Murali, M. D. Stoller, K. J. Ganesh, W. W. Cai, P. J. Ferreira, A. Pirkle, R. M. Wallace, K. A. Cychosz, M. Thommes, D. Su, E. A. Stach and R. S. Ruoff, Science, 2011, 332, 1537; (d) S. Stankovich, D. A. Dikin, G. H. B. Dommett, K. M. Kohlhaas, E. J. Zimney, E. A. Stach, R. D. Piner, S. T. Nguyen and R. S. Ruoff, Nature, 2006, 442, 282; (e) X. An and J. C. Yu, RSC Adv., 2011, 1, 1426; (f) M. S. Xu, D. Fujita and N. Hanagata, Small, 2009, 5, 2638; (g) S. Garaj, W. Hubbard, A. Reina, J. Kong, D. Branton and J. A. Golovchenko, Nature, 2010, 467, 190.
5. (a) Y. Zheng and T. Ando, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 245420; (b) K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197; (c) M. I. Katsnelson, K. S. Novoselov and A. K. Geim, Nat. Phys., 2006, 2, 620; (d) S. Y. Zhou, G. H. Gwenon, J. Graf, A. V. Ferdorov, C. D. Spataru, R. D. Diehl, Y. Kopelevich, D. H. Lee, D. H. Louie and A. Lanzara, Nat. Phys., 2006, 2, 595; (e) K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang and S. V. Dubonos, et al., Science, 2004, 306, 666; (f) A. A. Balandin, S. Ghosh, W. Bao, I. Calizo, D. Teweldebrhan and F. Miao, et al., Nano Lett., 2008, 8, 902; (g) C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385.
6. F. Withers, M. Dubois and A. K. Savchenko, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 73403.
7. (a) A. Dasgupta, S. Bera, F. Evers and M. J. van Setten, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125433; (b) S. Thongrattanasiri, A. Manjavacas and F. Javier García de Abajo, ACS Nano, 2012, 6, 1766.
8. (a) B. Yang, J. A. Boscoboinik, X. Yu, S. Shaikhutdinov and H.-J. Freund, Nano Lett., 2013, 13, 4422; (b) A. Bostwick, T. Ohta, J. L. McChesney, K. V. Emtsev, T. Seyller, K. Horn and E. Rotenberg, New J. Phys., 2007, 9, 385; (c) X. Dong, Y. Shi, Y. Zhao, D. Chen, J. Ye, Y. Yao, F. Gao, Z. Ni, T. Yu, Z. Shen, Y. Huang, P. Chen and L.-J. Li, Phys. Rev. Lett., 2009, 102, 135501; (d) R. Skomski, P. A. Dowben, M. S. Driver and J. A. Kelber, Mater. Horiz., 2014, 1, 563.
9. (a) L. D. Carr and M. T. Lusk, Nat. Nanotechnol., 2010, 5, 316; (b) S. Perumal, B. Minaev and H. Agren, J. Chem. Phys., 2012, 136, 104702; (c) B. Hajgató and M. S. Deleuze, Chem. Phys. Lett., 2012, 553, 6; (d) S. S. R. K. C. Yamijala, A. Bandhyopadyay and S. K. Pati, Chem. Phys. Lett., 2014, 603, 28; (e) P. A. Denis, R. Facciob and F. Iribarne, Comput. Theor. Chem., 2012, 995, 1; (f) P. A. Denis and F. Iribarne, J. Phys. Chem. C, 2013, 117, 19048.
10. (a) P. Rani and V. K. Jindal, RSC Adv., 2013, 3, 802; (b) P. A. Denis, Chem. Phys. Lett., 2010, 492, 251; (c) P. Shemella and S. K. Nayak, Appl. Phys. Lett., 2009, 94, 032101; (d) G. Giovannetti, P. A. Khomyakov, G. Brocks, V. M. Karpan, J. van den Brink and P. J. Kelly, Phys. Rev. Lett., 2008, 101, 026803; (e) J. Lin, J. Zhong, J. R. Kyle, M. Penchev, M. Ozkan and C. S. Ozkan, Nanotechnology, 2011, 22, 355701; (f) P. A. Denis, J. Phys. Chem. C, 2011, 115, 13392; (g) P. A. Denis, ChemPhysChem, 2014, 15, 3994; (h) P. A. Denis and C. P. Huelmo, Carbon, 2015, 87, 106.
11. (a) V. H. Crespi, L. X. Benedict, M. L. Cohen and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 13303; (b) B. R. Sharma, A. Manjanath and A. K. Singh, Sci. Rep., 2014, 4, 7164; (c) H. Terrones, M. Terrones, E. Hernández, N. Grobert, J.-C. Charlier and P. M. Ajayan, Phys. Rev. Lett., 2000, 84, 1716; (d) M. A. Hudspeth, B. W. Whitman, V. Barone and J. E. Peralta, ACS Nano, 2010, 4, 4565; (e) P. A. Denis, J. Phys. Chem. C, 2014, 118, 24976; (f) N. N. Karaush, G. V. Baryshnikov and B. F. Minaev, Chem. Phys. Lett., 2014, 612, 229.
12. (a) G. Brunetto, P. A. S. Autreto, L. D. Machado, B. I. Santos, R. P. B. dos Santos and D. S. Galvão, J. Phys. Chem. C, 2012, 116, 12810; (b) Y. Liu, G. Wang, Q. Huang, L. Guo and X. Chen, Phys. Rev. Lett., 2012, 108, 225505; (c) H. Huang, Y. Li, Z. Liu, J. Wu and W. Duan, Phys. Rev. Lett., 2013, 110, 029603.
13. (a) J. Nisar, X. Jiang, B. Pathak, J. Zhao, T. W. Kang and R. Ahuja, Nanotechnology, 2012, 23, 385704; (b) D. Li, F. Tian, B. Chu, D. Duan, S. Wei, Y. Lv, H. Zhang, L. Wang, N. Lu, B. Liua and T. Cui, J. Mater. Chem. A, 2015, 3, 10448; (c) K. Umemoto, R. M. Wentzcovitch, S. Saito and T. Miyake, Phys. Rev. Lett., 2010, 104, 125504; (d) Q. Li, Y. Ma, A. R. Oganov, H. Wang, H. Wang, Y. Xu, T. Cui, H.-K. Mao and G. Zou, Phys. Rev. Lett., 2009, 102, 175506; (e) Z. Zhao, B. Xu, X.-F. Zhou, L.-M. Wang, B. Wen, J. He, Z. Liu, H.-T. Wang and Y. Tian, Phys. Rev. Lett., 2011, 107, 215502; (f) F. Tian, X. Dong, Z. Zhao, J. He and H.-T. Wang, J. Phys.: Condens. Matter, 2012, 24, 165504; (g) J.-T. Wang, C. F. Chen and Y. Kawazoe, Phys. Rev. Lett., 2011, 106, 075501.
14. (a) S. Zhang, Q. Wang, X. Chen and P. Jena, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 18809; (b) S. Zhang, J. Zhou, Q. Wang, X. Chend, Y. Kawazoe and P. Jena, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2772; (c) Z. Wang, X.-F. Zhou, X. Zhang, Q. Zhu, H. Dong, M. Zhao and A. R. Oganov, Nano Lett., 2015, 15, 6182.
15. (a) K. S. Novoselov, D. Jiang, F. Schedin, T. J. Booth, V. V. Khotkevich, S. V. Morozov and A. K. Geim, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10451; (b) A. Kara, H. Enriquez, A. P. Seitsonen, L. C. Lew Yan Voon, S. Vizzini, B. Aufray and H. Oughaddou, Surf. Sci. Rep., 2012, 67, 1; (c) P. A. Denis, Phys. Chem. Chem. Phys., 2015, 17, 5393; (d) M. Xu, T. Liang, M. Shi and H. Chen, Chem. Rev., 2013, 113, 3766; (e) A. Ueno, T. Fujita, M. Matsue, H. Yanagisawa, C. Oshima, F. Patthey, H. C. Ploigt, W. D. Schneider and S. Otani, Surf. Sci., 2006, 600, 3518; (f) M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Adv. Mater., 2011, 23, 4248; (g) M. Naguib, O. Mashtalir, J. Carle, V. Presser, J. Lu, L. Hultman, Y. Gogotsi and M. W. Barsoum, ACS Nano, 2012, 6, 1322.
16. (a) L. Grill, M. Dyer, L. Lafferentz, M. Persson, M. V. Peters and S. Hecht, Nat. Nanotechnol., 2007, 2, 687; (b) J. Yu, Q. Sun, Y. Kawazoe and P. Jena, Nanoscale, 2014, 6, 14962; (c) G. V. Baryshnikov, B. F. Minaev, N. N. Karaush and V. A. Minaeva, Phys. Chem. Chem. Phys., 2014, 16, 6555; (d) G. V. Baryshnikov, B. F. Minaev, N. N. Karaush and V. A. Minaeva, RSC Adv., 2014, 4, 25843; (e) N. N. Karaush, G. V. Baryshnikov and B. F. Minaev, RSC Adv., 2015, 5, 24299; (f) N. N. Karaush, G. V. Baryshnikov, V. A. Minaeva and B. F. Minaev, New J. Chem., 2015, 39, 7815.
17. (a) H. Zeng, C. Zhi, Z. Zhang, X. Wei, X. Wang, W. Guo, Y. Bando and D. Golberg, Nano Lett., 2010, 10, 5049; (b) M. Wu, X. Wu, Y. Pei and X. C. Zeng, Nano Res., 2011, 4, 233; (c) Y. Lin and J. W. Connellb, Nanoscale, 2012, 4, 6908; (d) D. Sundholm, L. N. Wirzb and P. Schwerdtfeger, Nanoscale, 2015, 7, 15886.
18. (a) S. N. Monteiro, A. L. Diegues Skury, M. G. de Azevedo and G. S. Bobrovnitchii, J. Mater. Res. Technol., 2013, 2, 68; (b) O. Hod, J. Chem. Theory Comput., 2012, 8, 1360; (c) R. T. Paine and C. K. Narula, Chem. Rev., 1990, 90, 73; (d) D. Golberg, Y. Bando, O. Stephan and K. Kurashima, Appl. Phys. Lett., 1998, 73, 2441; (e) N. G. Chopra, R. J. Luyken, K. Cherrey, V. H. Crespi, M. L. Cohen, S. G. Louie and A. Zettl, Science, 1995, 269, 966.
19. (a) H. Wang, Q. Li, T. Cui, Y. Ma and G. Zou, Solid State Commun., 2009, 149, 843; (b) B. Wen, J. Zhao, R. Melnik and Y. Tian, Phys. Chem. Chem. Phys., 2011, 13, 14565; (c) C. He, L. Sun, C. Zhang, X. Peng, K. Zhang and J. Zhong, Phys. Chem. Chem. Phys., 2012, 14, 10971; (d) Y. Liu, X. Zou and B. I. Yakobson, ACS Nano, 2012, 6, 7053; (e) X. Jiang, J. Zhao and R. Ahuja, J. Phys.: Condens. Matter, 2013, 25, 122204; (f) Z. Li and F. Gao, Phys. Chem. Chem. Phys., 2012, 14, 869; (g) X. Zhang, Y. Wang, J. Lv, C. Zhu, Q. Li, M. Zhang, Q. Li and Y. Ma, J. Chem. Phys., 2013, 138, 114101; (h) Z. Zhang, M. Lu, L. Zhu, L. Zhu, Y. Li, M. Zhang and Q. Li, Phys. Lett. A, 2014, 378, 741.
20. (a) M. A. Hudspeth, B. W. Whitman, V. Barone and J. E. Peralta, ACS Nano, 2010, 4, 4565; (b) X.-Q. Wang, H.-D. Lib and J.-T. Wang, Phys. Chem. Chem. Phys., 2013, 15, 2024; (c) F. Schlütter, T. Nishiuchi, V. Enkelmann and K. Müllen, Angew. Chem., Int. Ed., 2014, 53, 1538.
21. (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785; (c) R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650; (d) M. S. Gordon, J. S. Binkley, J. A. Pople, W. J. Pietro and W. J. Hehre, J. Am. Chem. Soc., 1982, 104, 2797.
22. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, revision C.02, Gaussian, Inc., Wallingford, CT, 2009.
23. (a) A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899; (b) E. D. Glendening, A. E. Reed, J. E. Carp enter and F. Weinhold, J. Am. Chem. Soc., 1998, 120, 12051.
24. (a) R. F. W. Bader, Atoms in Molecules. A Quantum Theory, Calendon Press, Oxford, 1990; (b) R. F. W. Bader and H. Essen, J. Chem. Phys., 1984, 80, 1943; (c) R. F. W. Bader, T. S. Slee, D. Cremer and E. Kraka, J. Am. Chem. Soc., 1983, 105, 5061; (d) C. L. Firme, O. A. C. Antunes and P. M. Esteves, Chem. Phys. Lett., 2009, 468, 129.
25. (a) E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170; (b) E. Espinosa, I. Alkorta and I. Rozas, Chem. Phys. Lett., 2001, 336, 457; (c) L. N. Puntus, K. A. Lyssenko, M. Y. Antipin and J.-C. G. Bünzli, Inorg. Chem., 2008, 47, 11095; (d) A. O. Borissova, M. Y. Antipin, H. A. Karapetyan, A. M. Petrosyan and K. A. Lyssenko, Mendeleev Commun., 2010, 20, 260; (e) G. V. Baryshnikov, B. F. Minaev, V. A. Minaeva and V. G. Nenajdenko, J. Mol. Model., 2013, 19, 4511.
26. D. Cremer and E. Kraka, Croat. Chem. Acta, 1984, 57, 1259.
27. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567.
28. Materials Studio 5.5, Accelrys, Inc., San Diego, CA, 2008.
29. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
30. (a) T. P. Kaloni and S. Mukherjee, Mod. Phys. Lett. B, 2011, 25, 1855; (b) CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton, 79th edn, 1998.
31. (a) E. P. Carr, L. W. Pickett and D. Voris, J. Am. Chem. Soc., 1941, 63, 3231; (b) J. W. Hilpern, Trans. Faraday Soc., 1965, 61, 605; (c) J. Lüder, M. de Simone, R. Totani, M. Coreno, C. Grazioli, B. Sanyal, O. Eriksson, B. Brena and C. Puglia, J. Chem. Phys., 2015, 142, 074305; (d) T. Itoh, Chem. Rev., 2012, 112, 4541.
32. A. A. Fokin, L. V. Chernish, P. A. Gunchenko, E. Y. Tikhonchuk, H. Hausmann, M. Serafin, J. E. P. Dahl, R. M. K. Carlson and P. R. Schreiner, J. Am. Chem. Soc., 2012, 134, 13641.
33. (a) C. S. Liu, R. Jia, X. J. Ye and Z. Zeng, J. Chem. Phys., 2013, 139, 034704; (b) D. Jose and A. Datta, J. Phys. Chem. C, 2012, 116, 24639; (c) C. Chowdhury, S. Jahiruddin and A. Datta, J. Phys. Chem. Lett., 2016, 7, 1288.
34. Q. H. Wang, K. Kalantar-Zadeh, A. Kis, J. N. Coleman and M. S. Strano, Nat. Nanotechnol., 2012, 7, 699.
35. (a) L. Liua and Z. Shen, Appl. Phys. Lett., 2009, 95, 252104; (b) P. Ruffieux, et al., ACS Nano, 2012, 6, 6930; (c) R. Gutzler and D. F. Perepichka, J. Am. Chem. Soc., 2013, 135, 16585.
36. (a) S. Zhang, Z. Yan, Y. Li, Z. Chen and H. Zeng, Angew. Chem., Int. Ed. Engl., 2015, 54, 3112; (b) M. Zhang, G. Gao, A. Kutana, Y. Wang, X. Zou, J. S. Tse, B. I. Yakobson, H. Li, H. Liu and Y. Ma, Nanoscale, 2015, 7, 12023; (c) J. Millán, P. Godignon and A. Pérez-Tomás, Automatika, 2012, 53, 107.

---

Footnote

† Electronic supplementary information (ESI) available: Total energy of the ground singlet state for the Bp- and BN compounds; selected vertical transitions for the 1D and 2D Bp- and BN compounds; optimized structures and corresponding Cartesian coordinates for the Bp- and BN compounds. See DOI: 10.1039/c6ra06832d

---